مصورسازی پیچیدگی الگوریتم ها با پایتون – راهنمای کاربردی

در این مطلب، مبحث پیچیدگی الگوریتم ها که با نماد $$O(n)$$ نیز نمایش داده می‌شود، مورد بررسی قرار می‌گیرد. پیچیدگی الگوریتم ها یک مفهوم بسیار پیچیده در حوزه «علوم کامپیوتر» (Computer Science) محسوب می‌شود. برخورداری از «پس‌زمینه» (Background) ریاضی مناسب، برای درک مفاهیم بسیار سنگین پیچیدگی الگوریتم ها بسیار ضروری است. فهم و درک مبحث پیچیدگی الگوریتم‌ها به قدری سخت و طاقت فرسا است که حتی با به کارگیری استدلال‌های ریاضی قانع کننده، باز هم ممکن است درک این مفهوم برای بسیاری از افراد آسان نباشد.

در این مطلب، یک برنامه کوچک نوشته شده به زبان پایتون معرفی خواهد شد که می‌توان از آن برای مصورسازی پیچیدگی نسبی تعدادی از توابع مرسوم در برنامه‌نویسی استفاده کرد. ویژگی مهم برنامه این است که می‌توان به راحتی (و با تغییرات اندکی) از آن برای مصورسازی پیچیدگی دیگر الگوریتم‌ها استفاده کرد.

چرا محاسبه پیچیدگی الگوریتم ها اهمیت دارد؟

«پیچیدگی محاسباتی» (Computational Complexity) موضوع بسیار قابل توجهی در حوزه علوم کامپیوتر به شمار می‌آید. دلیل این امر، پیچیدگی بیش از حد مبانی ریاضی آن است که سبب شده درک آن، حتی برای دانشمندان علم داده و کامپیوترِ آشنا و مسلط به مفاهیم ریاضی سخت باشد. به بیان ساده، پیچیدگی الگوریتم ها در قالب مقدار زمان و فضای ذخیره‌سازی مورد نیاز الگوریتم برای حل یک نمونه از مسأله مورد نظر یا مجموعه‌ای از مسائل تعریف می‌شود.

شالوده پیچیدگی محاسباتی الگوریتم‌ها، مفاهیم ریاضی هستند؛ با این حال، پیامدهای مبحث محاسبه پیچیدگی الگوریتم‌ها برای حوزه علوم کامپیوتر بسیار حیاتی و البته کاربردی است. دسته‌ای از مسائل در حوزه علوم کامپیوتر وجود دارند که «غیر قابل مهار» (Intractable) هستند؛ حل کردن این دسته از مسائل، غیر ممکن نیست ولی الگوریتم کارآمد و بهینه‌ای برای حل آن‌ها ارائه نشده است. به عبارت دیگر، حل کردن این دسته از مسائل با فناوری‌های عصر حاضر (و حتی فناوری‌هایی که در آینده نزدیک ارائه خواهند شد)، بسیار سخت و از لحاظ محاسباتی و صرف منابع ناکارآمد خواهد بود.

پیچیدگی بدترین حالت

یکی از محبوب‌ترین رویکردهای محاسبه پیچیدگی الگوریتم ها در علوم کامپیوتر و مبحث پیچیدگی محاسباتی، پیچیدگی «سناریوی بدترین حالت» (Worst-Case Scenario) است. بر خلاف طبیعت «بدبینانه» (Pessimism) این دیدگاه، فلسفه آن بسیار منطقی است؛ اندازه مسأله‌ای که مایل به حل آن هستیم، با گذر زمان افزایش پیدا می‌کند. در غالب کاربردهای پردازش اطلاعات، حجم عظیمی از اطلاعات («پتابایت» (PetaByte) داده) مورد پردازش قرار می‌گیرد. بنابراین، اندازه داده‌هایی که قرار است برای حل مسأله مورد پردازش قرار بگیرد، یکی از فاکتورهای مهم در تعیین پیچیدگی الگوریتم‌ها است.

برای چنین کاری کافی است تا اندازه ورودی‌های مسأله را به عنوان یک «متغیر مستقل» (Independent Variable) و نرخ رشد اندازه ورودی‌ها را به عنوان یک «متغیر وابسته» (Dependent Variable) در نظر بگیرید؛ حالا عملکرد و پیچیدگی الگوریتم ها را وقتی که اندازه ورودی‌ها به سمت بی‌نهایت میل می‌کند اندازه بگیرید. به چنین تحلیلی، تحلیل big-Oh نیز گفته می‌شود.

تحلیل big-Oh، قواعد بسیار زیادی دارد که برای مطالعه آن‌ها می‌توانید به کتاب‌های حوزه علوم کامپیوتر و به ویژه «طراحی الگوریتم» (Algorithm Design) مراجعه کنید. یکی از مهم‌ترین قوانین تحلیل big-Oh این است که در مواقعی که اندازه ورودی‌‌ها بسیار بزرگ است، «ثابت‌های» (Constants) یک الگوریتم، تأثیری در عملکرد آن نخواهند داشت. دلیل این امر، اندازه ورودی‌ها است. اندازه ورودی‌ها، یکی از فاکتورهای مهم در تعیین پیچیدگی الگوریتم‌ها است و ثابت‌های الگوریتم به اندازه ورودی‌ها وابسته نیستند.

مقایسه پیچیدگی نسبی الگوریتم‌ها در پایتون

یکی از موضوعاتی که باعث سردرگمی برنامه‌نویسان مبتدی و یا افراد تازه وارد به حوزه پیچیدگی محاسباتی می‌شود این واقعیت است که توابع «نمایی» (Exponential) نظیر $$e ^ { n }$$، از لحاظ پیچیدگی محاسباتی بدتر از توابع «چند جمله‌ای» (Polynomial) نظیر $$n ^ { 100 }$$ هستند. چنین مسأله‌ای یکی از نمونه‌های بارز تعریف ریاضی و به کارگیری دیدگاه big-Oh محسوب می‌شود و برای درک آن لازم است تا $$n$$ را یک مقدار بسیار بزرگ تصور کنیم.

کدهای برنامه پایتون که در ادامه نمایش داده شده است، نرخ رشد پیچیدگی توابع را در حالتی نشان می‌دهد که پارامتر «نمونه مسأله» (Problem Instance) یا N افزایش پیدا می‌کند. برای نشان دادن نرخ رشد پیچیدگی از چهار تابع زیر استفاده شده است:

• تابع $$\log { n }$$
• تابع $$n$$
• تابع $$n ^ { 3 }$$
• تابع $$e ^ { n }$$

شایان توجه است که تابع $$n ^ { 3 }$$ از لحاظ عملکرد یک تابع بد محسوب می‌شود. به عنوان نمونه، چنین تابعی برای پردازش 1000 ورودی به $$10 ^ { 9 }$$ عملیات نیاز دارد. به طور کلی، برای $$k \geq 2$$، یک مسأله با پیچیدگی $$n ^ { k }$$، یک مسأله بد از لحاظ عملکرد و پیچیدگی محاسباتی محسوب می‌شود.

قطعه کد زیر، از کتابخانه‌های برنامه‌نویسی NumPy و MatPlotLib استفاده می‌کند و از تکنیک «برنامه‌نویسی تابعی» (Functional Programming) به نام currying برای محاسبه $$n ^ { k }$$ به ازاء ثابت $$k$$ استفاده می‌کند. با استفاده از قطعه کد زیر و تغییر لیست FUNCTIONS، به راحتی می‌توان پیچیدگی محاسباتی توابع دیگر را محاسبه کرد.

نتایج محاسبه شده برای پیچیدگی توابع در شکل‌های زیر نمایش داده شده است. تابع لگاریتم با رنگ فیروزه‌ای، توابع چند جمله‌ای با رنگ‌های آبی، ارغوانی و زرد و تابع نمایی با رنگ قرمز نمایش داده شده‌اند. در تمامی نمودارهای نمایش داده شده، محور عمودی، اندازه نسبی پیچیدگی محاسبه شده و محور عمودی، گذر زمان را نمایش می‌دهد. شایان توجه است که در مبحث پیچیدگی الگوریتم ها و محاسبه پیچیدگی محاسباتی، گذر زمان مترادف با افزایش ورودی‌های مسأله است. به عبارت دیگر، با گذر زمان، تعداد ورودی‌هایی که باید توسط مسأله مورد پردازش قرار بگیرد نیز به شدت افزایش می‌یابد.

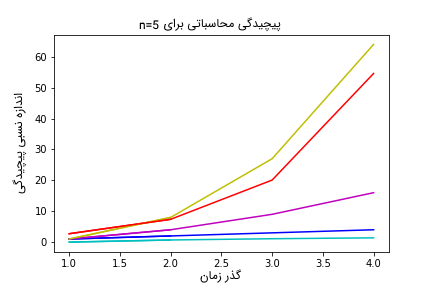
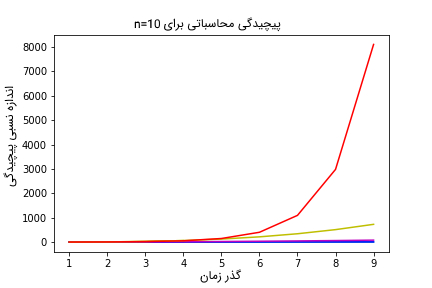
نتایج نمایش داده شده تعجب‌برانگیز نیست؛ تابع نمایی بدترین عملکرد را از نظر پیچیدگی محاسباتی، از خود نشان می‌دهد. همچنین، با گذر زمان و افزایش ورودی‌های پردازشی، پیچیدگی محاسباتی آن به شدت افزایش می‌یابد. برای حالتی که N=20 است، پیچیدگی محاسباتی توابع دیگر در مقابل تابع نمایی بسیار ناچیز است.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

مجموعه آموزش‌های مرتبط با زبان برنامه‌نویسی پایتون که در مجله فرادرس تهیه شده‌اند و برای عموم مخاطبان و خوانندگان در دسترس قرار گرفته‌اند، در اینجا گردآوری شده‌اند. در صورتی که تمایل دارید با زبان برنامه‌نویسی پایتون و نحوه کدنویسی در این زبان آشنا شوید، توصیه می‌شود که آموزش‌های ارائه شده در این مطب را مطالعه کنید.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• گنجینه آموزش‌های برنامه نویسی پایتون (Python)
• مجموعه آموزش‌های برنامه‌نویسی
• مجموعه آموزش‌های کاربردی برنامه‌نویسی C#‎ (سی‌شارپ)
• زبان برنامه نویسی پایتون (Python) — از صفر تا صد
• ترفندهای برنامه نویسی در پایتون — از صفر تا صد
• آموزش پایتون (Python) — مجموعه مقالات جامع وبلاگ فرادرس

^^