توزیع یکنواخت گسسته و پیوسته — مفاهیم و کاربردها

در نظریه احتمال، توزیع‌های متغیرهای تصادفی از اهمیت زیادی برای شناخت پدیده‌های تصادفی برخوردارند. از این میان «توزیع یکنواخت گسسته» (Discrete Uniform Distribution) و «توزیع یکنواخت پیوسته» (Continuous Uniform Distribution) نیز کاربردهای زیادی بخصوص در شبیه‌سازی داده‌های مربوط به توزیع‌های آماری دیگر دارند. به همین علت در این نوشتار به بررسی این دو توزیع آماری پرداخته، خصوصیات هر یک را توضیح خواهیم داد.

برای درک بهتر این نوشتار بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید.

توزیع یکنواخت

در مطالب وبلاگ فرادرس که مربوط به متغیر تصادفی است، توضیحاتی درباره تکیه‌گاه متغیر تصادفی آورده شده است. در آنجا توضیح داده شد که نوع مقادیر تکیه‌گاه مشخص می‌کند که متغیر تصادفی یا توزیع آن از نوع گسسته یا پیوسته است. به این ترتیب دو نوع توزیع یکنواخت خواهیم داشت. توزیع یکنواخت گسسته با مقادیر تکیه‌گاه که به صورت مجموعه $$S=\{1,2,3,\cdots,n\}$$ مشخص شده است و  توزیع یکنواخت پیوسته که تکیه‌گاه آن به صورت یک فاصله از اعداد حقیقی مثلا $$(a,b)$$ است.

فیلم آموزش آمار و احتمالات مهندسی – حل نمونه سوالات کنکور ارشد در فرادرس

کلیک کنید

ولی چیزی که باعث شده هر دوی این توزیع‌ها، یکنواخت نامیده شوند، «تابع احتمال» (Probability Function) یا «تابع چگالی» (Density Function) آن‌ها است که برای همه نقاط مربوط به تکیه‌گاه ثابت است.

نکته: اگر متغیر تصادفی یا توزیع آن، گسسته باشد، برای محاسبه احتمال در هر نقطه از تابع احتمال استفاده می‌شود. در صورتی که متغیر تصادفی یا توزیع آن پیوسته باشد، تابع چگالی، جرم احتمال در هر نقطه را بیان می‌کند.

حال به بررسی هر یک از این توزیع‌ها می‌پردازیم.

توزیع یکنواخت گسسته (Discrete Uniform Distribution)

فرض کنید تکیه‌گاه متغیر تصادفی X شامل n نقطه و به صورت $$S=\{1,2,3,\cdots,n\}$$ باشد. اگر تابع احتمال این متغیر تصادفی به شکل زیر نوشته شود به آن توزیع یکنواخت گسسته می‌گویند.

$$\large f_X(x)=P(X=x)=\frac{1}{n}\;, x\in S$$

همانطور که دیده می‌شود، برای هر نقطه از اعداد صحیح بین ۱ تا n،‌ مقدار احتمال ثابت است. با توجه به این شیوه برای بیان توزیع یکنواخت، برای محاسبه احتمال تنها به پارامتر n احتیاج است.

برای نمایش تابع توزیع احتمال تجمعی چنین متغیر تصادفی می‌توان از رابطه زیر استفاده کرد.

$$\large F_X(x)=P(X\leq x)=\frac{[x]}{n},\;\;x\in S$$

نکته: منظور از $$[x]$$، جزء صحیح مقدار x است که بزرگترین مقدار صحیحی را نشان می دهد که از x کوچکتر است.

مثال

یک تاس را پرتاب می‌کنیم. اگر X نشان دهنده عدد مشاهده شده هنگام نشستن تاس باشد، می‌توان توزیع احتمال آن را یکنواخت از نوع گسسته دانست. زیرا در این حالت n=6 بوده و می‌توان نوشت:

$$\large S=\{1,2,3,4,5,6\}$$

$$f_X(x)=P(X=1)=P(X=2)=P(X=3)=P(X=4)=P(X=5)=P(X=6)=\frac{1}{6}$$

$$\large F_X(x)=\frac{x}{6}$$

در حالتی که قبلا به آن اشاره شد، مقدار تابع احتمال متغیر تصادفی یکنواخت گسسته با تنها یک پارامتر که همان (n) است، قابل محاسبه خواهد بود. ولی می‌توان از روش دیگری که البته معادل حالت قبلی محسوب می‌شود نیز برای نشان دادن تابع احتمال و یا تعریف متغیر تصادفی یکنواخت گسسته استفاده کرد. در این حالت تکیه‌گاه متغیر تصادفی X را تعداد اعداد صحیح در فاصله $$[a,b]$$ در نظر می‌گیریم و می‌نویسیم $$X\sim U\{a,b\}$$ و می‌خوانیم X دارای توزیع یکنواخت گسسته با پارامترهای a و b است. واضح است که در این حالت، مقدار n را می‌توان به صورت زیر محاسبه کرد.

$$\large n=b-a+1$$

باید توجه داشت که در این حالت، همیشه b>a است و داریم:

$$\large a\in \{\cdots ,-2,-1,0,1,2,\dots \}\,$$

$$\large b\in \{\dots ,-2,-1,0,1,2,\cdots \},b\geq a$$

$$\large S=\{k\mid k\in \{a,a+1,\dots ,b-1,b\}\,\}$$

تابع احتمال و تابع توزیع احتمال تجمعی در این حالت به صورت زیر نوشته می‌شود:

$$\large f_X(x)=P(X=x)=\frac{1}{n} ,\;\;x\in S$$

$$\large F_X(x;a,b)=P(X\leq x)= \frac{[x]-a+1}{n}$$

مثال

می‌خواهیم به یازده دانش‌آموز یک کلاس به صورت تصادفی نمره‌ای با مقدارهای صحیح از ۱۰ تا ۲۰ بدهیم. برای اینکه این نمرات به صورت یکنواخت بینشان توزیع شود، از توزیع یکنواخت گسسته با پارامترهای ۱۰ و ۲۰ کمک می‌گیریم. در این صورت اگر X نمره یک دانش‌آموز باشد، خواهیم داشت:

$$\large a=10,\; b=20$$

$$\large n=20-10+1=11$$

$$\large S=\{10,11,12,13,14,15,16,17,18,19,20\}$$

$$\large f_X(x)=\frac{1}{11}$$

$$\large F_X(x)=P(X\leq x)=\frac{[x]-10+1}{11}$$

بنابراین احتمال آنکه نمره دانش‌آموزی کمتر از ۱۵.5 باشد برابر است با

$$\large F_X(15.5)=P(X\leq 15.5)=\frac{[15.5]-10+1}{11}=\frac{15-10+1}{11}=\frac{6}{11}$$

نمودار مربوط به تابع احتمال این توزیع به شکل زیر است:

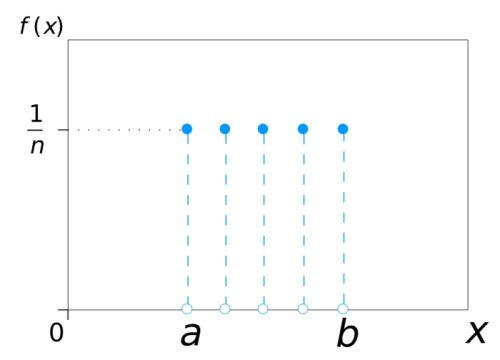
همانطور که دیده می‌شود، این نمودار متقارن است در نتیجه میزان چولگی آن صفر خواهد بود. نمودار تابع احتمال تجمعی برای چنین توزیعی در تصویر زیر دیده می‌شود.

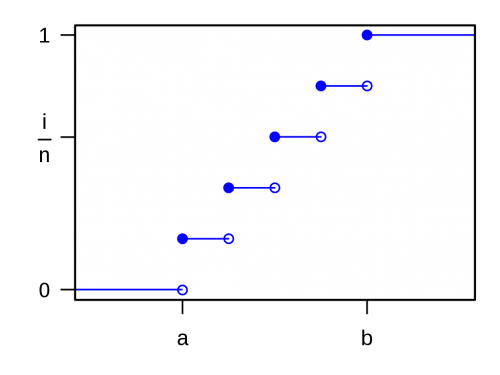
باید توجه داشت که در این جا، میزان پرش‌ها در هر نقطه بیانگر میزان احتمال در آن نقطه است.

خصوصیات توزیع یکنواخت گسسته

درست به مانند توزیع‌های دیگر آماری، برای توزیع یکنواخت می‌توان امید ریاضی و واریانس را محاسبه کرد. در ادامه به بررسی این ویژگی‌ها می‌پردازیم.

فیلم آموزش مسائل تشریحی توزیع های گسسته و پیوسته در آمار و احتمال (رایگان) در فرادرس

کلیک کنید

امید ریاضی

شیوه محاسبه امید ریاضی برای متغیرهای تصادفی گسسته، در مطلب مربوط به امید ریاضی در وبلاگ فرادرس قابل مشاهده است. در اینجا نیز با استفاده از همان توضیحات، امید ریاضی برای متغیر تصادفی یکنواخت گسسته را محاسبه می‌کنیم.

$$\large E(X)=\sum_{x=1}^n xP(X=x)=\sum_{x=1}^n x\frac{1}{n}=\frac{1}{n}\sum_{x=1}^n x=(\frac{1}{n})(\frac{n(n+1)}{2})=\frac{n+1}{2}$$

نکته: برای محاسبه جمع مقدارهای x از ۱ تا n از تصاعد حسابی استفاده کرده‌ایم.

شیوه محاسبه امید ریاضی برای متغیر تصادفی گسسته یکنواخت که تابع احتمال آن به فرم دوم نشان داده شده باشد نیز به همین شکل است. یعنی می‌توان نوشت:

$$\large E(X)=\sum_{x=a}^b xP(X=x)=\sum_{x=a}^b x\frac{1}{n}=\frac{1}{n}\sum_{x=a}^b x=$$
$$\large (\frac{1}{n})(\frac{n}{2}(2a+(n-1))=\frac{1}{2}(a+(a+n-1))=\frac{(a+b)}{2}$$

همانطور که دیده می‌شود، باز هم از تصاعد حسابی برای انجام محاسبه کمک گرفته شده است.

مثال: در مثال مربوط به دانش‌آموزان، متوسط نمرات برابر با ۱۵ خواهد بود زیرا:

$$\large E(X)=\frac{(a+b)}{2}=\frac{(10+20)}{2}=\frac{30}{2}=15$$

واریانس

از آنجایی که می‌دانیم واریانس متغیر تصادفی X را می‌توان به صورت تفاضل امیدریاضی مربع آن از مربع امید ریاضی محاسبه کرد، می‌توان محاسبه واریانس را برای متغیر تصادفی یکنواخت به صورت زیر نوشت:

$$\large Var(X)=E(X^2)-E(X)^2=\frac{n^2-1}{12}$$

و برای شیوه دوم نمایش تابع احتمال برای متغیر تصادفی یکنواخت گسسته خواهیم داشت:

$$\large Var(X)=\frac{(b-a+1)^2-1}{12}$$

در نتیجه برای مثال دانش‌آموزان، واریانس نمرات برابر است با:

$$\large Var(X)=\frac{(20-10+1)^2-1}{12}=\frac{11^2}{12}=\frac{121}{12}=10.083$$

نکته: البته در اینجا نیز از تصاعد زیر برای محاسبه واریانس کمک گرفته شده است:

$$\large S^2_n=1^2+2^2+3^2+\cdots+n^2=\frac{n(n+1)(2n+1)}{6}$$

یک مثال کاربردی

در بسیاری از تحلیل‌های آماری، مایل به برآورد پارامتر یا پارامترهای توزیع به کمک یک نمونه هستیم. در این قسمت نیز به کمک یک مثال، سعی داریم برآورد پارامتر توزیع یکنواخت گسسته را پیدا کنیم. در این مثال یک نمونه به اندازه k از جامعه‌ای با توزیع یکنواخت گسسته با پارامتر N گرفته شده است و هدف برآورد پارامتر N است. اغلب این مثال را با نام مسئله تانک‌های آلمانی می‌شناسند زیرا با توجه به برآورد حداکثر تعداد، می‌توان تعداد تانک‌های آلمانی تولید شده در جنگ جهانی دوم را برآورد کرد.

برای N، «برآوردگر نااریب با کمترین واریانس» (Uniformly Minimum Variance Unbiased Estimator) یا UMVUE به صورت زیر تعریف می شود.

$$\large \widehat{N}=\frac{k+1}{k}m-1=m+\frac{m}{k}-1$$

که در آن m مقدار بزرگترین مقدار مشاهده شده در نمونه و k نیز اندازه نمونه بدون جایگذاری است.

در این حالت فرض شده است که تانک‌ها دارای شماره سریال از ۱ تا N هستند. و احتمال آنکه تانک iام به غنیمت گرفته شود دارای توزیع یکنواخت است. یعنی داریم:

$$\large P(X=i)=\frac{1}{N}$$

فرض کنید در یک حمله ۴ تانک به غنیمت گرفته شده‌اند که دارای شماره‌ سریال‌های 19، 40، 42 و ۶۰ هستند. لازم است تعداد کل تانک‌ها یعنی N، برآورد شود. بزرگترین شماره در بین سریال ها ۶۰ است در نتیجه داریم m=60. از طرفی برای تعداد نمونه نیز داریم k=4. پس تعداد کل تانکها با توجه به توزیع یکنواخت به صورت زیر برآورد می‌شود:

$$\large N\approx 60+\frac{60}{4}-1=74$$

توزیع یکنواخت پیوسته (Continuous Uniform Distribution)

فرض کنید X یک متغیر تصادفی پیوسته است که تکیه‌گاه آن به صورت $$S=(a,b)$$ نوشته شده است. اگر تابع چگالی این متغیر تصادفی به صورت زیر نوشته شود، می‌گوییم متغیر تصادفی X دارای توزیع یکنواخت پیوسته است و می‌نویسیم $$X\sim U(a,b)$$.

$$\large f_X(x)=\frac{1}{b-a} , \;\;a\leq x\leq b$$

واضح است که برای مقادیری از x که در خارج بازه (a,b) قرار گرفته باشند، تابع چگالی برابر با صفر است. گاهی به چنین توزیعی، توزیع مستطیلی (Rectangular Distribution) نیز گفته می‌شود.

با توجه به پیوستگی متغیر تصادفی و تابع چگالی آن، برای پیدا کردن تابع توزیع تجمعی این متغیر تصادفی باید از انتگرال تابع چگالی احتمال استفاده کرد. در نتیجه خواهیم داشت:

$$\large F_X(x)=\int_{a}^x\frac{1}{b-a}\;dx=\frac{x-a}{b-a}, \;\;a\leq x\leq b$$

مشخص است که برای مقدارهایی از x که کمتر از a هستند، تابع توزیع احتمال تجمعی برابر با صفر و برای مقدارهای بزرگتر از b نیز برابر با ۱ خواهد بود. در این حالت، فرم صحیح برای تابع توزیع تجمعی متغیر تصادفی یکنواخت پیوسته به صورت زیر خواهد بود؛

$$\large F(x)={\begin{cases}0&{\text{for }}xb\end{cases}}$$

در حقیقت می‌توان تابع توزیع را نسبت فاصله نقطه x از مبدا به کل طول یا فاصله a تا b در نظر گرفت. این مقدارها در «نظریه اندازه‌ها» (Measure Theory)، اندازه لبگ (Lebesgue measure) نامیده می‌شوند. نمودار مربوط به تابع چگالی این متغیر تصادفی به صورت زیر است.

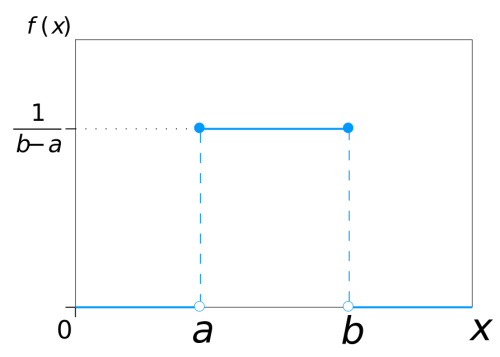
همانطور که دیده می‌شود، تابع چگالی حول میانگین یا مرکز توزیع متقارن است. در نتیجه چولگی برای آن صفر است. شکل تابع توزیع تجمعی برای این متغیر تصادفی نیز در شکل زیر دیده می‌شود.

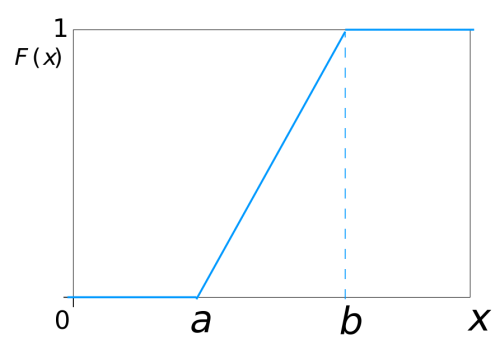
مثال

فرض کنید، فردی به طور تصادفی به سمت مرکز یک خط با طول 2 متر به عنوان هدف تیراندازی می‌کند. احتمال اینکه فاصله محل اثابت گلوله او از مرکز کمتر از 0.2 متر باشد به صورت زیر محاسبه می شود.

با توجه به خصوصیات تابع توزیع تجمعی و قواعد محاسبه احتمال، از آنجایی که می‌دانیم طول خط 2 متر است، مرکز آن را نقطه 1 در نظر گرفته و می‌توان X را یک متغیر تصادفی با توزیع یکنواخت به شکل $$X\sim U(0,2)$$ در نظر گرفت. در نتیجه فاصله محل اصابت تا مرکز به صورت $$|X-1|$$ قابل محاسبه است. به این ترتیب خواهیم داشت:

$$\large P(|X-1|<0.2)=P(-0.2$$

$$\large F_X(1.2)-F_X(0.8)= \frac{1.2-0}{2}-\frac{0.8-0}{2}=0.6-0.4=0.2$$

خصوصیات توزیع یکنواخت پیوسته

درست به مانند دیگر توزیع‌ها، مهمترین خصوصیات توزیع یکنواخت پیوسته، امید ریاضی و واریانس آن است.

فیلم آموزش آنالیز داده های چند متغیره با نرم افزار Unscrambler X در فرادرس

کلیک کنید

امید ریاضی

به کمک انتگرال‌گیری، امید ریاضی برای توزیع یکنواخت پیوسته به صورت زیر محاسبه می‌شود.

$$\large E(X)=\int_a^b x\frac{1}{b-1}\;dx=\frac{1}{b-a}(\frac{1}{2})x^2\mid_a^b=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2}$$

بنابراین برای مثال قبل، متوسط فاصله گلوله شلیک شده تا هدف برابر است با: $$\frac{2+0}{2}=1$$

واریانس

باز هم شبیه شیوه‌ای که برای محاسبه واریانس برای متغیر تصادفی یکنواخت گسسته به کار بردیم را در اینجا تکرار می‌کنیم. یعنی می‌نویسیم:

$$\large Var(X)=E(X^2)-E(X)^2=\int_a^b x^2\frac{1}{b-1}\;dx-\frac{(a+b)^2}{4}=$$
$$\large \frac{1}{3}x^3\mid_a^b-\frac{(a+b)^2}{4}=\frac{1}{3}(b^3-a^3)-\frac{1}{4}(a+b)^2=\frac{1}{12}(b-a)^2$$

یکی از حالت‌های خاص برای توزیع یکنواخت پیوسته، زمانی است که پارامترهای آن به صورت a=0 و b=1 باشند. در این حالت توزیع را یکنواخت پیوسته استاندارد می‌نامند و بوسیله $$U(0,1)$$ نشان می‌هند. خاصیت جالبی که این متغیر تصادفی دارد این است که اگر $$X\sim U(0,1)$$ باشد آنگاه $$1-X\sim U(0,1)$$ است.

ارتباط با توزیع‌های دیگر

توزیع یکنواخت پیوسته با بسیاری از توزیع‌ها در ارتباط است. مهم‌ترین آن‌ها را می‌توان توزیع احتمالی برای تابع توزیع احتمال تجمعی در نظر گرفت. در این حالت اگر X یک متغیر تصادفی با توزیع $$F_X(x)$$ باشد می‌توان نوشت:

$$\large U=F_X(x)\sim U(0,1)$$

یعنی تابع توزیع تجمعی هر متغیر تصادفی دارای توزیع یکنواخت پیوسته با پارامترهای ۰ و ۱ است. این قضیه کمک می‌کند که با استفاده از معکوس تابع توزیع، اعداد تصادفی از هر توزیع دلخواه تولید شود. البته این تکنیک در زمانی قابل استفاده است که معکوس تابع توزیع مورد نظر وجود داشته و دارای فرم بسته باشد.

همچنین اگر X دارای توزیع یکنواخت استاندارد باشد (a=0, b =1) آنگاه می‌توان توزیع متغیر تصادفی X را به صورت توزیع بتا در نظر گرفت و نوشت $$X\sim Beta(1,1)$$. پس یکنواخت، حالت خاصی از توزیع بتا است.

شبیه‌سازی داده از توزیع‌های دیگر

در حل بسیاری از مسائل و بررسی‌های آزمایشگاهی، لازم است که تحلیل‌هایی روی داده‌های شبیه‌سازی شده صورت گیرد. بسیاری از زبان‌های برنامه‌نویسی، تابع یا توابعی دارند که برای تولید اعداد تصادفی به کار گرفته می‌شوند. معمولا توزیع تصادفی برای این اعداد، نرمال استاندارد در نظر گرفته می‌شود. به این ترتیب اعداد تصادفی تولید شده در فاصله ۰ تا ۱ هستند.

اگر لازم باشد مقدار تصادفی X در فاصله a تا b ایجاد شود، ابتدا یک عدد تصادفی به نام U از توزیع یکنواخت استاندارد تولید شده و به کمک رابطه X= a+(b-a)U عدد مورد نظر در فاصله a تا b ساخته می‌شود. در این حالت X دارای توزیع یکنواخت پیوسته در فاصله a تا b خواهد بود.

تولید اعداد تصادفی با توزیع یکنواخت به کمک اکسل

فرض کنید می‌خواهید عددی تصادفی در فاصله ۰ تا ۱ در یک سلول از کاربرگ اکسل قرار دهید. تابع $$rand()$$ به راحتی و بدون هیچ پارامتری عدد تصادفی از توزیع یکنواخت تولید می‌کند.

اگر می‌خواهید عدد تصادفی از توزیع یکنواخت گسسته تولید کنید، کافی است از تابع $$randbetween(bottom,top)$$ استفاده کنید. پارامترهای این تابع به ترتیب bottom و top هستند که اولی برای مشخص کردن کران پایین عدد و دومی برای مشخص کردن کران بالای عدد در نظر گرفته می‌شود. ذکر این نکته نیز ضروری است که مقدار پارامتر bottom حتما باید از top کمتر باشد. البته امکان درج مقدارهای منفی برای پارامترهای این تابع نیز وجود دارد.

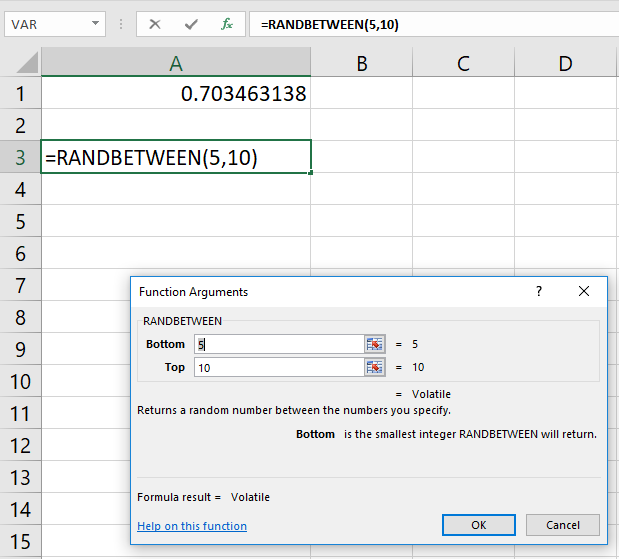
نکته: باید توجه داشت که با تغییر یا ورود اطلاعات هر سلولی از کاربرگ، مقدارهای این سلول‌ها که به صورت تصادفی ایجاده شده‌اند، مجدد محاسبه شده و عدد تصادفی جدیدی ظاهر خواهد شد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آزمایش تصادفی، پیشامد و تابع احتمال
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^