توضیح توان در ریاضیات – به زبان ساده
ما به طور معمول این گونه یاد گرفتهایم که توان همان تکرار ضرب است که البته توضیح مقدماتی خوبی محسوب میشود؛ اما با این توضیح در مورد و یا چه میتوان گفت؟ چگونه میتوان صفر را صفر بار در خودش ضرب کرد و نتیجهای برابر با 1 به دست آورد؟

واقعیت این است که با تعریف توان به صورت تکرار ضرب نمیتوان برای سؤالهای فوق پاسخی یافت. شما با مطالعه این نوشته دیدگاه تازهای نسبت به توانها به دست میآورید و میتوانید معنی سؤالهای فوق را به خوبی درک کنید.
مدل بهروز شده ذهنی
| عملیات | مفهوم قدیمی | مفهوم جدید |
|---|---|---|
| جمع | تکرار شمارش | لغزش |
| ضرب | تکرار جمع | مقیاسبندی |
| توان | تکرار ضرب | رشد برای مدت معین |
حساب مانند نوعی تبدیل است
اینک یک گام به عقب برمیداریم و به خاطر میآوریم که در ابتدا چگونه حساب را آموختهایم؟ به ما یاد دادهاند که اعداد برای شمارش اشیا (مثلاً انگشتها) به کار میآیند، جمع نیز ترکیبی از شمارشها (7 = 4 + 3) و ضرب تکرارِ جمع است (2 ضرب در 3 = 2 + 2 + 2 = 6)
جمع مکرر هنگامی که مشغول ضرب با اعداد رُندی مانند 2 و 10 هستیم معنیدار است؛ اما وقتی از اعدادی مانند 1- یا چنین نیست.
دلیل آن این است که مدل ما کامل نیست. اعداد صرفاً شماره نیستند. دیدگاه بهتر موقعیتی روی یک خط است. این موقعیت میتواند منفی (1-) بین دو عدد () یا در بعد دیگر (i) باشد.
حساب روشی برای تبدیل عدد محسوب میشود. جمع مانند لغزش است یعنی وقتی میگوییم با 3 جمع کنید یعنی باید 3 واحد به سمت راست بلغزیم. ضرب نیز مقیاسبندی است، بدین صورت که ضرب در 3 به معنی مقیاسبندی تا 3x است. اما در مورد توان چه میشود گفت؟
دستگاه Expand-o-tron 3000

فرض کنید دستگاهی شبیه به میکروویو داریم که آن را Expand-o-tron 3000 مینامیم؛ اما وظیفه این دستگاه به جای گرما دادن به غذاها، رشد دادن اعداد است. کافی است عددی را در آن قرار دهید تا پس از مدتی عدد جدیدی بیرون آید. روش کار چنین است:
- با 1.0 آغاز میکنیم.
- میزان رشد را برابر تغییر مطلوب پس از یک ثانیه قرار میدهیم (2x، 3x، 10.3x).
- زمان را برابر با تعداد ثانیهها قرار دهید.
- دکمه دستگاه را بزنید.
زمانی که کار این دستگاه پایان یابد یک عدد کاملاً جدید خواهیم داشت. فرض کنید میخواهیم 1.0 را به 9 تغییر دهیم:
- 1.0 را در دستگاه Expand-o-tron قرار میدهیم.
- تغییر را برابر با 3x و زمان را به مدت 2 ثانیه تنظیم میکنیم.
- دکمه را میزنیم.
عدد شروع به تبدیل شدن میکند و میبینیم که به صورت 1.0، 1.1، 1.2 و ... رشد مییابد تا این که در انتهای ثانیه اول به عدد 3.0 میرسد. اما چون دستگاه روی 2 ثانیه تنظیم شده به رشد خود ادامه میدهد. در انتهای ثانیه دوم ما عدد 9.0 را داریم. اینک عدد جدید ما آماده است.
از نظر ریاضیاتی Expand-o-tron 3000 (تابع نمایی) کارهای زیر را انجام میدهد:

یا

برای نمونه . پایه توان مقداری است که میخواهیم رشد یابد (3x) و نما نیز مدت زمان رشد را تعیین میکند (2). فرمولی مانند به این معنی است که از دستگاه Expand-o-tron برای رشد 2 به مدت n ثانیه استفاده کنید.
ما هنگام استفاده از Expand-o-tron همواره از 1.0 آغاز میکنیم تا ببینیم یک مقدار واحد چگونه تغییر مییابد. اگر بخواهید ببینید وقتی از 3.0 در Expand-o-tron آغاز میکنیم چه رخ میدهد، باید نتیجه نهایی را نیز مقیاسبندی کنیم. برای نمونه
آغاز از 1 و دو برابر کردن به میزان 3 مرتبه یعنی
آغاز از 3 و دو برابر کردن به میزان 3 مرتبه یعنی
هرزمان که دیدید صرفاً از یک نما استفاده شده است، بدانید که باید از مقدار واحد 1 آغاز کنیم.
درک عامل مقیاسبندی نمایی
هنگام ضرب کردن میتوانیم صرفاً عامل مقیاسبندی نهایی را تعیین کنیم. اگر میخواهید عددی 8 برابر شود، کافی است آن را در 8 ضرب کنید. اما توانها کمی متفاوت هستند.
دستگاه expand-o-tron ماهیتی غیر مستقیم دارد و صرفاً با تماشای آن نمیتوانید متوجه شوید که چه کاری انجام میدهد. به نظر شما معنی چه میتواند باشد؟ در واقع توان به جای یک عامل مقیاسبندی میخواهد که شما رشد را کاملاً درک و حس کنید.
اما چرا توان این قدر متفاوت است. شاید یکی از دلایل آن این باشد که اغلب چیزها در طبیعت نمیدانند که تا کجا رشد خواهند کرد.
برای مثال آیا فکر میکنید که باکتریها از قبل برنامهریزی کردهاند که هر 14 ساعت دو برابر شوند؟ نه چنین نیست. باکتریها صرفاً شروع به خوردن کپک روی غذایی میکنند که فراموش کردهاید سریعاً در یخچال بگذارید و ما صرفاً از میزان رشد کنونی آنها سعی میکنیم حدس بزنیم که چه مدت طول میکشد تا آنها به مقدار مشخصی برسند.
بنابراین برای یافتن پاسخ باید زحمت کشید. در واقع در مورد توان ما یک مقدار آغازین را در نظر میگیریم و شروع به تغییر میکنیم تا ببینیم به کجا میرسیم. دستگاه expand-o-tron (یا ماشینحساب ما) صرفاً با بررسی اعداد نمیتواند عامل مقیاسبندی نهایی را درک کند؛ اما به هر حال باید کسی این کار را انجام دهد.
درک توانهای کسری
در این بخش میخواهیم ببینیم آیا expand-o-tron واقعاً به ما کمک میکند که توانها را درک کنیم؟ ابتدا بگویید که در مورد چه فکر میکنید؟
زمانی که در مورد ضرب مکرر فکر کنیم، همه چیز سردرگمکننده میشود. اما آن را ساده میکند. 1.5 مقدار زمانی است که این دستگاه برای رشد نیاز دارد.
- یعنی به دستگاه 1 ثانیه فرصت میدهیم (رشد 2x)
- یعنی به دستگاه 2 ثانیه فرصت میدهیم (رشد 4x)
یعنی به دستگاه 1.5 ثانیه فرصت میدهیم و از این رو رشد به میزان عددی بین 2 تا 4 برابر خواهد بود. ایده «شمارش مکرر» ما را وامیدارد که از اعداد کامل استفاده کنیم؛ اما با فرض دستگاه expand-o-tron ثانیههای کسری نیز کاملاً معنیدار هستند.
ضرب کردن توانها
اگر بخواهیم چرخههای رشد چندگانه را محاسبه کنیم چه باید بکنیم؟ فرض کنید از دستگاه به مدت 2 ثانیه استفاده میکنیم، سپس دقیقاً با همان توان به مدت 3 ثانیه از آن استفاده میکنیم:
اگر به دستگاه میکروویو معمولی فکر کنیم، این وضعیت مانند یک چرخه 5 ثانیهای پیوسته است. تا زمانی که تنظیمات توان (پایه) یکسان بماند، میتوانیم زمانها را با هم جمع کنیم:
در این مورد نیز expand-o-tron عامل مقیاسبندی را برای تغییر دادن عدد در اختیار ما میگذارد. برای دریافت نتیجه کلی از دو کاربرد متوالی میتوانیم عاملهای مقیاسبندی را در هم ضرب کنیم.
جذر
اینک فرض کنید یک رشد با مبنای a و زمان 3 ثانیه داریم:
اکنون اگر میزان زمان را نصف یعنی 1.5 ثانیه تعیین کنیم، مقدار رشد چه قدر خواهد بود؟
سپس اگر این زمان را دو برابر کنیم، چه رخ میدهد؟
رشد کلی = رشد جزئی × رشد جزئی
با نگاه کردن به معادله فوق میبینیم که «رشد جزئی» جذر رشد کلی است. در واقع اگر زمان را نصف کنیم، به جذر عامل مقیاسبندی دست مییابیم و اگر زمان را یکسوم کنیم:
رشد کلی = رشد جزئی × رشد جزئی × رشد جزئی
بدین ترتیب به ریشه سوم میرسیم. این دلیل شهودی خوبی است که چرا وقتی نماها را تقسیم میکنیم به ریشههای عددی میرسیم. ما زمان را به قطعههای مساوی تقسیم میکنیم و از این رو هر دوره «رشد جزئی» تأثیر یکسانی دارد. اگر سه تأثیر یکسان را درهم ضرب کنیم، به این معنی است که هر یک، ریشه سوم عدد هستند.
توانهای منفی
اکنون نوبت آن رسیده است که معنای توان منفی را بررسی کنیم. ثانیههای منفی یعنی حرکت رو به عقب در زمان. اگر حرکت رو به جلو باعث رشد شود، حرکت رو عقب باعث کوچک شدن میشود:
جمله فوق به این معنا است که «1 ثانیه قبل در نیمه مقدار کنونی بودهایم (). در واقع این بخشی از هر نمودار نمایی مانند است.
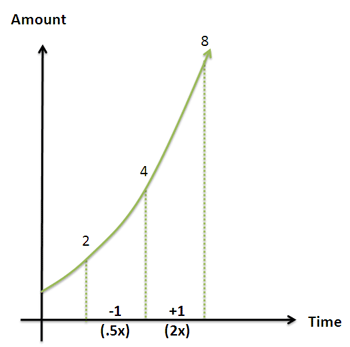
یک نقطه مانند 3.5 ثانیه را انتخاب کنید (). یک ثانیه حرکت به سوی آینده باعث رشد دو برابری مقدار کنونی میشود (). یک ثانیه قبل باعث میشود مقدار فعلی نصف شود ().
این وضعیت برای هر عددی پاسخ میدهد. اگر اینک 1 میلیون داشته باشیم، یک ثانیه قبل 500،000 داشتهایم.
بررسی توان صفر
اکنون به بررسی برخی مفاهیم غامضتر میپردازیم. معنی چیست؟ معنای آن این است که دستگاه خود را روی رشد 3x تنظیم میکنیم و از آن به مدت صفر ثانیه استفاده میکنیم. در واقع صفر ثانیه به این معنی است که اصلاً از دستگاه استفاده نمیکنیم.
بنابراین مقادیر اولیه و نهایی ما یکسان هستند و از این رو عامل مقیاسبندی برابر با 1 است. استفاده از 0 به عنوان توان به این معنی است که هیچ تغییری رخ نمیدهد و عامل مقیاسبندی همواره 1 است.
بررسی مبنای صفر
اینک را چگونه میتوان تفسیر کرد؟ معنای آن این است که مقدار رشد 0x است و آن را پس از یک ثانیه اندازهگیری میکنیم. بدین ترتیب expand-o-tron عدد را گرفته و آن را به صفر تبدیل میکند. بدین ترتیب متوجه میشویم اگر چه ما یک ثانیه را بررسی کردیم؛ اما در واقع دستگاه پس از هر مدت زمانی عدد را صفر میکند:
یعنی n امین ریشه یعنی n امین ریشه 0 یعنی 0
مهم نیست که عدد را به چه توانی میرسانیم؛ در هر صورت ریشه چندم صفر خواهد بود.
توان با مبنا و نمای صفر
در نهایت معنای چیست؟
این بار نیز دستگاه expand-o-tron به کمک ما میآید. expand-o-tron یعنی رشد 0x به مدت 0 ثانیه. یعنی ما کلاً از دستگاه استفاده نمیکنیم و بدین ترتیب مقدار اولیه و نهایی یکسان خواهد بود، یعنی عامل مقیاسبندی برابر با 1 است. بنابراین . این رابطه مقدار اولیه را تغییر نمیدهد. بدین ترتیب راز آن گشوده میشود.
البته از نظر ریاضیدانها باعث میشود که قضایای زیادی کار کنند. در واقعیت 0 به سناریوی مورد بررسی که پیوسته یا گسسته باشد وابسته است و حقیقت آن محل بحث است. البته ما در مثال دستگاه میکروویو خود به دنبال اثبات قضایا نیستیم و صرفاً میخواهیم معنای شهودی گزارههای ریاضیاتی را درک کنیم.
مباحث پیشرفته: توانهای مکرر (A به توان B به توان C)
توانهای مکرر مبحث پیچیدهای محسوب میشوند. معنای عبارت زیر چیست؟
این عبارت به معنی تکرار ضرب مکرر است که روش دیگری برای بیان به توان رساندن مجدد یک عدد است. فرض کنید عبارت فوق به صورت زیر باشد:
- ابتدا با دو برابر کردن در طی هر ثانیه شروع میکنیم و این کار را برای 3 ثانیه انجام میدهیم
- سپس عددی که به دست آمده یعنی رشد 8x را به مدت 4 ثانیه رشد میدهیم ()
توان اول (3) فقط این را میداند که باید 2 را گرفته و آن را 3 بار در خودش ضرب کند. توان بعدی (4) میداند که مقدار قبلی را گرفته و به میزان 4 مرتبه رشد دهد. هر واحد زمانی در مرحله دوم همانند تکرار مرحله اول خواهد بود:
در این زمان تفسیر شمارش مکرر به کمک ما میآید؛ اما میتوانیم از expand-o-tron نیز کمک بگیریم: ما در فاز اول به مدت 3 ثانیه رشد میدهیم و سپس در فاز دوم این کار را به مدت 4 ثانیه تکرار میکنیم. این وضعیت در مورد توانهای کسری نیز پاسخ میدهد. برای مثال:
یعنی به مدت 3.1 ثانیه رشد دهیم و از آن نرخ رشد جدید به مدت 4.2 ثانیه استفاده کنیم. ما میتوانیم این دو زمان را به صورت زیر ترکیب کنیم:
این مفهوم متفاوتی است و از این رو چند مثال را بررسی میکنیم:
- یعنی 2 را به مدت 1 ثانیه رشد دهیم و این رشد را به مدت x ثانیه دیگر ادامه دهیم.
- یعنی میتوانیم به یکباره به 7 برسیم؛ یا این که میتوانیم طوری برنامهریزی کنیم که ابتدا به جذر 7 برسیم و سپس با رشد دو برابری به عدد کامل 7 برسیم.
بازنویسی توانها
دستگاه expand-o-tron ما از یک نظر دیگر نیز عجیب است، چون عددها وقتی داخل آن قرار میگیرند بیدرنگ رشد میکنند؛ اما ما رشد مطلوب را در انتهای هر ثانیه تعیین میکنیم.
ما میگوییم که میخواهیم در انتهای ثانیه اول رشد 2x داشته باشیم. اما از کجا باید بدانید که با چه نرخی باید رشد را شروع کنیم؟ در طی 0.5 ثانیه با چه سرعتی باید رشد کند؟
نکته کلیدی این است که منحنیهای رشد مانند از دیدگاه بیننده هستند و نه رشدکننده.
مقدار 2 در انتهای بازه اندازهگیری میشود و ما با حرکت به عقب توان را میسازیم. این وضعیت برای ما راحتتر است؛ اما نه برای کمیت در حال رشد. برای مثال باکتریها، عناصر رادیواکتیو یا پول، اهمیتی نمیدهند که ما برای بازههای زمانی معین چه برنامهریزی کردهایم.
این موجودات نه مقدار کنونی خود را میدانند و نه نرخ رشد پیوسته و تلاش نیز نمیکنند که در حد و مرزی که ما تعیین میکنیم بگنجند. در واقع این وضعیت شبیه درکی است که ما از رادیانها و درجهها داریم (+). رادیان طبیعی است چون از دیدگاه متحرک ثبت میشود.
برای این که دیدگاه رشدکننده را به دست آوریم باید از عدد جادویی e (+) استفاده کنیم. در این خصوص نکتههای بیشتری میتوان گفت؛ اما هر نوع فرمول با تمرکز روی بیننده مانند را میتوان به صورت زیر به فرمول از دیدگاه رشدکننده تبدیل کرد:
در این حالت، ln(2) =.693 = 69.3% نرخ رشد پیوسته مورد نیاز برای این است که رشد ما از دیدگاه بیننده به صورت به نظر برسد. زمانی که شما رشد 2x را در انتهای هر دوره تعین 0 ی میکنید، دستگاه expand-o-tron میداند که باید عدد را با نرخ 69.3% رشد دهد.
جزییات این موارد را به نوشته دیگری موکول میکنیم. فعلاً همین قدر که تفاوت بین نرخ رشد پیوسته رشدکننده و نمودار بیننده که در انتهای هر بازه اندازهگیری میشود را بدانید کافی است. در هر حال باید دانست که هر منحنی نمایی نسخه مقیاس یافتهای از محسوب میشود.
هر نما نسخهای از e است همانطور که هر عدد نسخهای از 1 محسوب میشود.
سخن پایانی
آیا واقعاً دستگاهی مانند expand-o-tron وجود دارد؟ آیا اعداد واقعاً روی یک خط گرد هم آمدهاند؟ پاسخ هر دو سؤال منفی است، اینها تنها مثالهایی از شیوه نگرش ما به دنیا هستند. دستگاه expand-o-tron حاصل تلاش ذهنی نگارنده این مقاله هست. هر چیزی از قواعد لغزش تا فرمول اویلر بر اساس اهمیت دادن به تفکرات شهودی به دست میآید.
اگر این نوشته برای شما مفید بوده است، پیشنهاد میکنیم آموزشهای زیر را نیز مطالعه کنید:
- مجموعه آموزشهای ریاضیات
- لگاریتم و هر آنچه باید دربارهش بدانید – معرفی مفاهیم پایه به زبان ساده
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- آموزش ریاضی پایه دانشگاهی
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
- آموزش ریاضیات عمومی ۱
==













جلّ الخالق !!!
خیلی عجیبه!