دوقطبی در مدارهای الکتریکی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در مدارهای الکتریکی، دو سر یا ترمینال (Terminal) که جریان به یکی از آن‌ها وارد و از دیگری خارج می‌شود، یک پورت، درگاه یا قطب (Port) را تشکیل می‌دهند. در نتیجه، دستگاه‌ها یا قطعات دوسر (مانند مقاومت، خازن و سلف)، شبکه‌هایی تک‌‌قطبی هستند (یک جفت سر دارند).

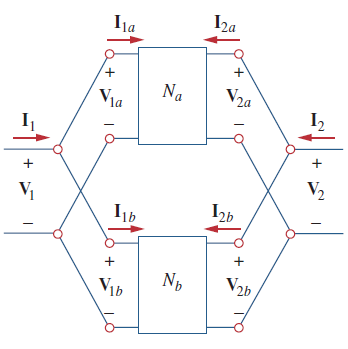
اغلب مدارهایی که با آن‌ها سروکار داریم، شبکه‌هایی دوسر یا تک‌قطبی هستند که تصویر نمادین آن‌ها در شکل ۱ (الف) نشان داده شده است. تقویت‌کننده‌های عملیاتی، ترانزیستورها و ترانسفورماتورها از مدارهای چهارسر یا دوقطبی هستند که شکل 1 (ب)، نماد کلی آن‌ها را نشان می‌دهد.

در حالت کلی، یک شبکه ممکن است $$n$$ قطب داشته باشد. قطب، یک دسترسی به شبکه است و از یک جفت سر تشکیل شده که جریان از یک سر وارد و از سر دیگر آن خارج می‌شود، بنابراین، جریان خالص قطب، صفر است.

در این آموزش، شبکه‌های دوقطبی (یه به‌طور ساده‌تر دوقطبی‌ها) را بررسی می‌کنیم.

شبکه دوقطبی، یک شبکه الکتریکی است که دو قطب مجزا برای ورودی و خروجی دارد.

قطعات سه‌سر مانند ترانزیستور را می‌توان در قالب دوقطبی پیکربندی کرد. دوقطبی‌ها، در مخابرات، سیستم‌های کنترل، سیستم‌های قدرت و الکترونیک کاربرد فراوانی دارند. برای مثال، در الکترونیک برای مدل کردن ترانزیستورها و تسهیل طراحی مدار به‌کار می‌روند. همچنین، با دانستن پارامترهای یک دوقطبی، می‌توان رفتار آن را به‌عنوان یک «جعبه سیاه» در شبکه‌های بزرگ تحلیل کرد.

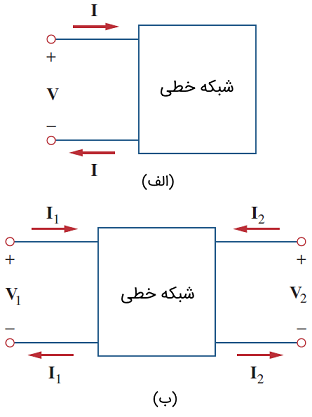
برای بیان مشخصات یک شبکه دوقطبی، باید ارتباط بین مقادیر مربوط به سرها ($$V_1$$، $$V_2$$، $$I_1$$ و $$I_2$$) شکل 1 (ب) را با یکدیگر پیدا کنیم که دو تا از آن‌ها مستقل از هم باشند. عبارات مختلفی که این ولتاژ و جریان‌ها را با هم مرتبط می‌کنند، پارامتر (Parameter) نامیده می‌شود. در این‌جا، فرض می‌کنیم، مدار دوقطبی، منبع وابسته ندارد، اما می‌تواند منبع مستقل داشته باشد.

پارامترهای امپدانس

امپدانس (Impedance) و ادمیتانس (Admittance)، در سنتز فیلتر‌ها استفاده می‌شوند.

همچنین، در تحلیل و طراحی شبکه‌های تطبیق امپدانس و شبکه‌های توزیع برق کاربرد دارند.

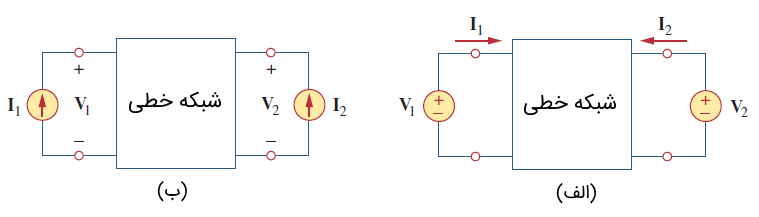
یک شبکه دوقطبی را می‌توان با منبع ولتاژ (شکل 2 (الف)) یا منبع جریان (شکل 2 (ب)) تغذیه کرد. ولتاژ ترمینال‌ها با روابط زیر بیان می‌شود:

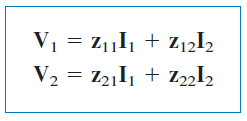
معادلات بالا را می‌توان به فرم ماتریسی زیر نوشت:

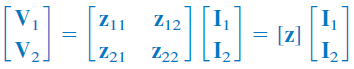
که در آن، عبارات $$z$$، پارامترهای امپدانس یا به‌طور ساده‌تر، پارامترهای z نامیده می‌شوند و واحد آن‌ها اهم است.

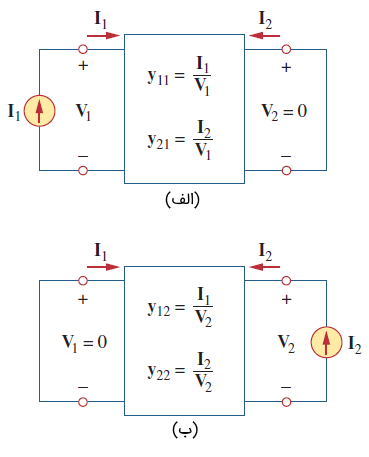
مقادیر این پارامترها را می‌توان با قرار دادن $$I_1=0$$ (قطب ورودی مدار باز) یا $$I_2=0$$ (قطب خروجی مدار باز) به‌دست آورد. بنابراین،

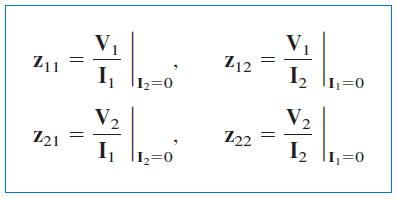
از آن‌جایی که پارامترهای $$z$$، از مدار باز کردن ورودی یا خروجی به‌دست می‌آیند، پارامترهای امپدانس مدار باز نیز نامیده می‌شوند. به‌طور خاص،

• $$z_{11}$$ = امپدانس ورودی مدار باز
• $$z_{12}$$ = امپدانس انتقالی مدار باز از قطب 1 به قطب ۲
• $$z_{21}$$ = امپدانس انتقالی مدار باز از قطب ۲ به قطب ۱
• $$z_{22}$$ = امپدانس خروجی مدار باز

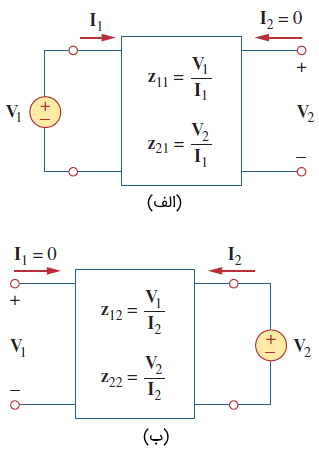
گاهی $$z_{11}$$ و $$z_{22}$$، امپدانس نقطه تحریک (Driving-point impedance) و $$z_{12}$$ و $$z_{21}$$، امپدانس انتقال (Transfer impedance) نامیده می‌شوند.

وقتی $$z_{11}=z_{22}$$، دوقطبی متقارن (Symmetrical) نامیده می‌شود. این، بدین معنی است که می‌توان خطی را یافت که شبکه را به دو قسمت مشابه تقسیم کند.

وقتی دوقطبی خطی باشد و منابع وابسته نداشته باشد، امپدانس‌های انتقالی برابر خواهند بود ($$z_{12}=z_{21}$$) و دوقطبی، متقابل (Reciprocal) یا هم‌پاسخ نامیده می‌شود. این، بدین معنی است که اگر نقاط تحریک و پاسخ را با یکدیگر تعویض کنیم، امپدانس‌ها انتقالی تغییری نمی‌کنند.

یک شبکه متقابل را می‌توان با مدار معادل $$T$$ آن جایگزین کرد که در شکل ۴ (الف) نشان داده شده است. اگر شبکه متقابل نباشد، مدار عمومی‌تر شکل ۴ (ب) را به‌جای آن به‌کار می‌بریم.

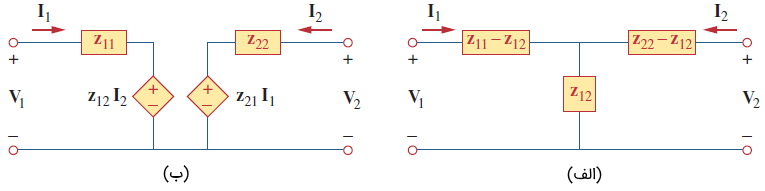
لازم به ذکر است که برخی شبکه‌ها، پارامتر امپدانس ندارند. برای مثال، ترانسفورماتور ایده‌آل شکل 5 را در نظر بگیرید:

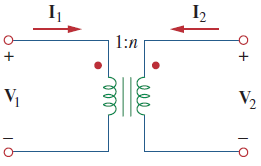
ترانسفورماتور شکل بالا، با روابط زیر بیان می‌شود:

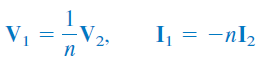
واضح است که نمی‌توان ولتاژ را برحسب جریان یا جریان را برحسب ولتاژ نوشت، بنابراین، ترانسفورماتور ایده‌آل، پارامتر امپدانس ندارد.

پارامترهای ادمیتانس

در بخش قبل دیدیم ممکن است پارامترهای امپدانس یک شبکه دوقطبی وجود نداشته باشد.

بنابراین، یک جایگزین لازم است که با آن بتوان چنین شبکه‌هایی را توصیف کرد. بنابراین، دسته دیگری از پارامترها را معرفی می‌کنیم که براساس توصیف جریان‌ها براساس ولتاژها امکان پذیر است.

مطابق شکل 6، می‌توان جریان‌ها را برحسب ولتاژ به‌صورت زیر نوشت:

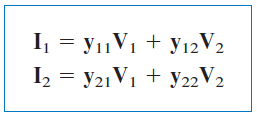
اگر معادلات بالا را به‌صورت ماتریسی بنویسیم، داریم:

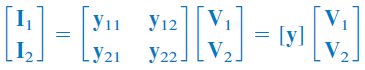
جملات $$y$$، به‌عنوان پارامترهای ادمیتانس (Admittance parameters) یا پارامترهای $$y$$ شناخته می‌شوند و واحد آن‌ها زیمنس است.

مقادیر این پارامترها را می‌توان با قرار دادن $$V_1=0$$ (ورودی اتصال کوتاه) یا $$V_2=0$$ (خروجی اتصال کوتاه) به‌دست آورد: بنابراین،

از آن‌جایی که پارامترهای $$y$$، با اتصال کوتاه کردن ورودی یا خروجی محاسبه می‌شوند، آن‌ها را پارامترهای ادمیتانس اتصال کوتاه نیز می‌نامند. به‌طور خاص،

• $$y_{11}$$ = ادمیتانس ورودی اتصال کوتاه
• $$y_{12}$$ = ادمیتانس انتقالی اتصال کوتاه از قطب ۲ به قطب ۱
• $$y_{21}$$ = ادمیتانس انتقالی اتصال کوتاه از قطب ۱ به قطب ۲
• $$y_{22}$$ = ادمیتانس ورودی اتصال کوتاه

مجموعه پارامترهای امپدانس و پارامترهای ادمیتانس، پارامترهای امیتانس (Immittance) نامیده می‌شوند.

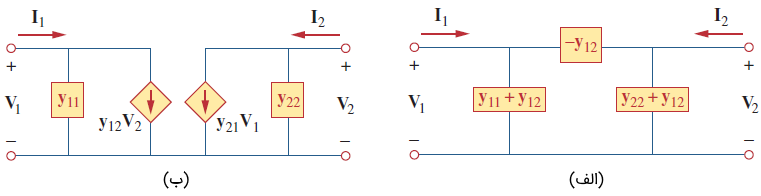
در یک شبکه دوقطبی خطی که منبع وابسته وجود نداشته باشد، ادمیتانس‌های انتقالی برابر هستند ($$y_{12}=y_{21}$$). این مورد، شبیه چیزی است که درباره پارامترهای امپدنس گفتیم. یک شبکه متقابل ($$y_{12}=y_{21}$$) را می‌توان مطابق شکل ۷ (الف) با مدار معادل $$\Pi$$ مدل کرد. اگر شبکه متقابل نباشد، می‌توان از مدار معادل عمومی شکل ۷ (ب) بهره برد.

پارامترهای هیبرید

ممکن است پارامترهای $$z$$ و $$y$$ یک شبکه دوقطبی همیشه وجود نداشته باشند.

بنابراین، لازم است پارامترهای دیگری را تعریف کرد. دسته سوم پارامترها، براساس متغیرهای وابسته $$V_1$$ و $$I_2$$ تعریف می‌شوند. بنابراین، داریم:

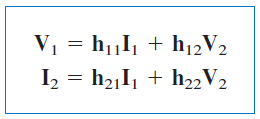
فرم ماتریسی معادلات بالا به‌صورت زیر است:

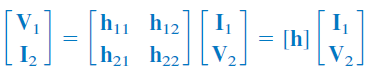
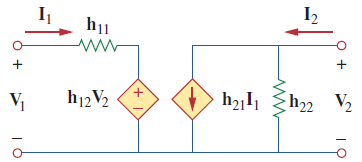
جملات $$h$$، پارامترهای هیبرید (Hybrid parameters) یا پارامترهای $$h$$ نامیده می‌شوند، زیرا ترکیباتی از نسبت‌های جریان و ولتاژ هستند. توصیف پارامترهای هیبرید، ابزار مفیدی برای توصیف قطعات الکترونیکی مانند ترانزیستور است. اندازه‌گیری پارامترهای $$h$$ به‌صورت تجربی، نسبت به اندازه‌گیری پارامترهای $$z$$ و $$y$$ کار آسانی است.

ترانسفورماتور شکل ۴ را به‌خاطر بیاورید که نتوانستیم آن را با پارامترهای $$z$$ توصیف کنیم. اگر به معادلات حاکم بر آن دقت کنیم، می‌بینیم که می‌توان آن‌ها را در قالب پارامترهای $$h$$ نوشت.

پارامترهای هیبرید، به‌صورت زیر تعیین می‌شوند:

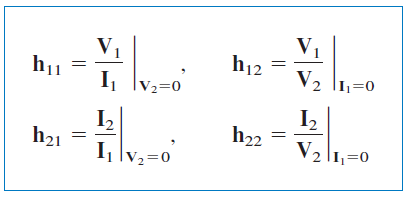
با توجه به معادلات بالا، می‌توان گفت پارامترهای $$h_{11}$$، $$h_{12}$$، $$h_{21}$$ و $$h_{22}$$، به‌ترتیب نشان‌دهنده امپدانس، بهره ولتاژ، بهره جریان و ادمیتانس هستند. به همین دلیل است که این پارامترها، هیبرید نامیده می‌شوند. به‌طور خاص،

• $$h_{11}$$ = امپدانس ورودی اتصال کوتاه
• $$h_{12}$$ = بهره ولتاژ‌ معکوس مدار باز
• $$h_{21}$$ = بهره جریان مستقیم اتصال کوتاه
• $$h_{22}$$ = ادمیتانس خروجی مدار باز

روند محاسبه پارامترهای $$h$$، شبیه محاسبه پارامترهای $$z$$ و $$y$$ است. بدین منظور، یک منبع ولتاژ یا جریان به یک طرف شبکه وصل کرده، سمت دیگر را اتصال کوتاه یا مدار باز می‌کنیم، سپس کمیت مورد نظر را اندازه می‌گیریم.

اگر $$h_{12}=-h_{21}$$، شبکه متقابل است. شکل 8، مدل هیبرید یک شبکه دوقطبی را نشان می‌دهد.

پارامترهای دیگری که ارتباط نزدیکی به پارامترهای $$h$$ دارند، پارامترهای $$g$$ یا پارامترهای هیبرید معکوس هستند. این پارامترها، برای توصیف جریان و ولتاژ شبکه به‌کار می‌رود:

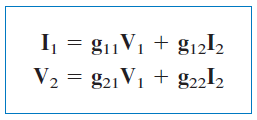
یا

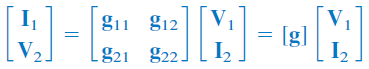
مفادیر پارامترهای $$g$$، با استفاده از روابط زیر محاسبه می‌شود:

به‌طور خاص، پارامترهای هیبرید معکوس را به‌صورت زیر نام‌گذاری می‌کنند:

• $$g_{11}$$ = ادمیتانس ورودی مدار باز
• $$g_{12}$$ = بهره جریان معکوس اتصال کوتاه
• $$g_{21}$$ = بهره ولتاژ مستقیم مدار باز
• $$g_{22}$$ = امپدانس خروجی اتصال کوتاه

شکل 9، مدل هیبرید معکوس یک شبکه دوقطبی را نشان می‌دهد. پارامترهای $$g$$، در مدل کردن ترانزیستورهای اثر میدان (FET) کاربرد دارند.

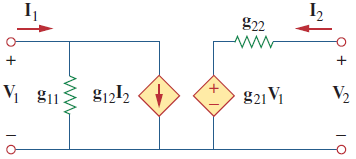
پارامترهای انتقال

از آن‌جایی که محدودیتی برای انتخاب جریان و ولتاژهای مستقل از هم یا وابسته به هم وجود ندارد، می‌توانیم مجموعه پارامترهای دیگری را نیز تعریف کنیم. یکی از این مجموعه پارامترها، متغیرهای ورودی را برحسب متغیرهای خروجی بیان می‌کند. بنابراین،

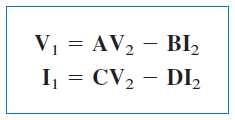
یا

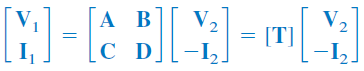
معادلات بالا، متغیرهای ورودی ($$V_1$$ و $$I_1$$) را به متغیرهای خروجی ($$V_2$$ و $$-I_2$$) ربط می‌دهند. بد نیست بدانید که در محاسبه پارامترهای انتقال،  $$-I_2$$ بیش‌تر از $$I_2$$ به‌کار می‌رود، زیرا جریان مورد نظر باید از مدار خارج شود (شکل 10). این نوع تعریف جهت جریان، در دوقطبی‌های پشت سر هم کاربرد دارد که خروجی یک دوقطبی، به ورودی دوقطبی دیگر وارد می‌شود. به همین دلیل، خارج شدن جریان $$I_2$$‌منطقی است. در سیستم‌های قدرت نیز، جریان را خارج‌شونده در نظر می‌گیرند.

یکی دیگر از مزایای پارامترهای انتقال این است که نشان می‌دهند ولتاژ و جریان چگونه از منبع به بار منتقل می‌شوند. این پارامترها، در تحلیل خطوط انتقال (مانند کابل‌ها) نیز مفید هستند، زیرا متغیرهای نقطه ارسال ($$V_1$$ و $$I_1$$) را برحسب پارامترهای نقطه دریافت ($$V_۲$$ و $$-I_2$$) بیان می‌کنند. به همین دلیل، پارامترهای انتقال نامیده می‌شوند. پارامترهای انتقال که پارامترهای ABCD نیز نامیده می‌شوند، در طراحی سیستم‌های تلفن، شبکه‌های مایکروویو و رادارها به‌کار می‌روند. این پارامترها را می‌توان به‌صورت زیر تعیین کرد:

هریک از پارامترهای انتقال را به‌صورت زیر نام‌گذاری می‌کنند:

• $$A$$ = نسبت ولتاژ‌ مدار باز
• $$B$$ = امپدانس انتقالی اتصال کوتاه منفی
• $$C$$ = ادمیتانس انتقالی مدار باز
• $$D$$ = نسبت جریان اتصال کوتاه منفی

$$A$$ و $$D$$ بدون بُعد هستند و $$B$$ و $$C$$، به‌ترتیب، برحسب اهم و زیمنس بیان می‌شوند.

دسته آخر پارامترها را می‌توان با تعریف متغیرهای خروجی برحسب متغیرهای ورودی بیان کرد. بنابراین، داریم:

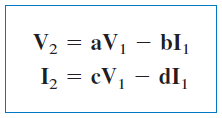
یا

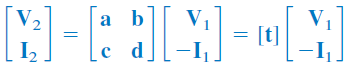
پارامترهای $$a$$، $$b$$، $$c$$ و $$d$$ پارامترهای انتقال معکوس یا پارامترهای $$t$$ نامیده می‌شوند. این پارامترها را می‌توان به‌صورت زیر تعیین کرد:

تعریف هریک از پارامترهای بالا، به‌شکل زیر است:

• $$a$$ = بهره ولتاژ مدار باز
• $$b$$ = امپدانس انتقالی اتصال کوتاه منفی
• $$c$$ = ادمیتانس انتقالی مدار باز
• $$d$$ = بهره جریان اتصال کوتاه منفی

پارامترهای $$a$$ و $$d$$ بدون بعد هستند و $$b$$ و $$c$$‌ به‌ترتیب، برحسب اهم و زیمنس بیان می‌شوند.

یک شبکه، متقابل است، اگر برای برای پارامترهای انتقال و انتقال معکوس داشته باشیم:

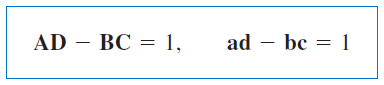
روابط بین پارامترها

از آن‌جایی که شش مجموعه پارامتر بیان شده، ورودی و خروجی‌های یکسانی را از دوقطبی‌های مشابه به هم مرتبط می‌کنند، می‌توان رابطه آن‌ها با یکدیگر را بیان کرد. اگر دو مجموعه پارامتر وجود داشته باشد، این امکان وجود دارد که یکی را به دیگری مرتبط کرد. با یک مثال، این کار را نشان می‌دهیم.

فرض کنید می‌خواهیم پارامترهای $$z$$‌ را براساس پارامترهای $$y$$ به‌دست آوریم. قبلاً پارامترهای $$z$$‌را به‌صورت زیر بیان کردیم:

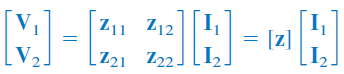
یا

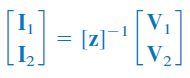
همچنین، برای پارامترهای $$y$$‌ داریم:

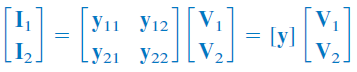
از دو رابطه اخیر می‌توان تساوی زیر را نتیجه گرفت:

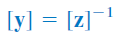
ماتریس الحاقی $$[z]$$ برابر است با

و دترمینان آن نیز به‌صورت زیر محاسبه می‌شود:

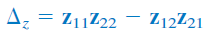
درنتیجه، می‌توان تساوی زیر را نوشت:

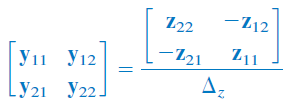
بنابراین، با برابر قرار دادن پارامترها، می‌توان پارامترهای $$y$$ را برحسب پارامترهای $$z$$ به‌دست آورد:

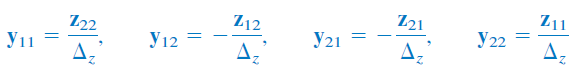
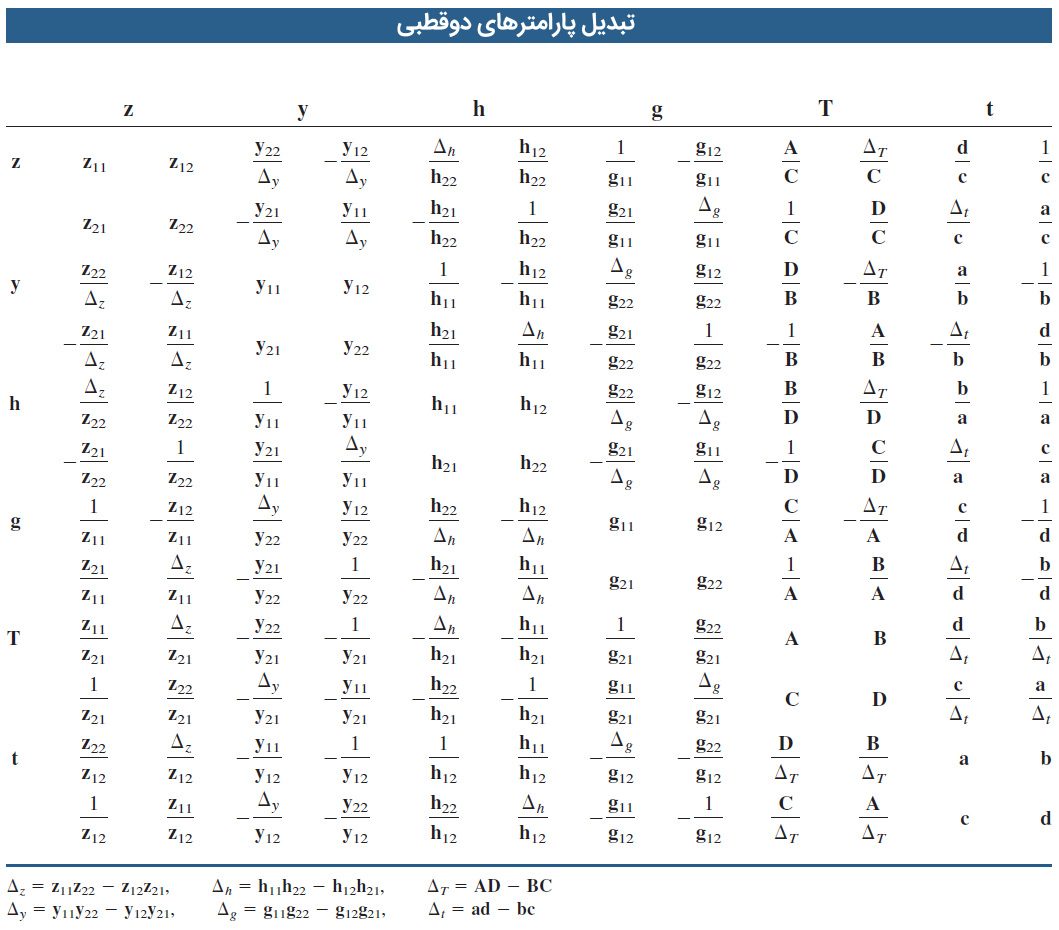
جدول زیر، فرمول‌های تبدیل شش مجموعه پارامتر دوقطبی‌ها را نشان می‌دهد. برای مثال، با داشتن پارامترهای $$T$$، می‌توانیم پارامترهای $$h$$‌ را از ستون پنجم ردیف سوم پیدا کنیم.

اتصال شبکه‌ها به یکدیگر

برای تحلیل و طراحی یک شبکه بزرگ پیچیده، می‌توان آن را به زیرشبکه‌ها تجزیه کرد. این زیرشبکه‌ها، با دوقطبی مدل می‌شوند که به یکدیگر متصل شده و شبکه اصلی را تشکیل می‌دهند. این اتصال ممکن است سری، موازی یا متوالی باشد. اگرچه، شبکه را می‌توان با شش مجموعه پارامتر توصیف کرد، اما، ممکن است یک دسته از آن‌ها نسبت به بقیه مزیت داشته باشد. برای مثال، وقتی شبکه‌ها سری هستند، پارامترهای $$z$$ آن‌ها با هم جمع شده و پارامتر $$z$$ شبکه بزرگ به‌دست می‌آید. همچنین، در حالتی که شبکه‌ها به‌صورت موازی متصل می‌شوند، پارامتر $$y$$‌ آن‌ها با یکدیگر جمع شده و پارامتر $$y$$ شبکه بزرگ‌تر را نشان می‌دهد. در حالتی اتصال متوالی نیز، پارامتر انتقال شبکه بزرگ‌تر، از حاصل‌ضرب پارامتر‌های انتقال شبکه‌های کوچک‌تر به‌دست می‌آید.

اتصال سری

اتصال سری دوقطبی‌ها در شکل 11 نشان داده شده است.

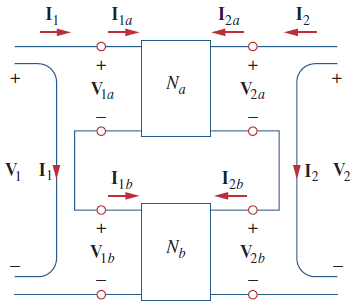
اتصال بین آن‌ها را به این دلیل سری می‌گوییم که جریان‌های ورودی هر دو با هم برابر بوده و ولتاژ آن‌ها جمع می‌شود. برای شبکه $$N_a$$ داریم:

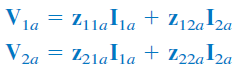
و برای شبکه $$N_b$$:

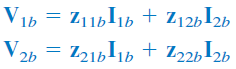
با توجه به روابطی که برای پارامترهای $$z$$ نوشتیم، برای شبکه شکل 11، داریم:

و

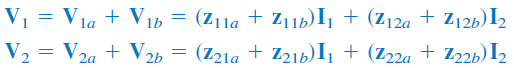
بنابراین، پارامترهای $$z$$ این شبکه برابر است با

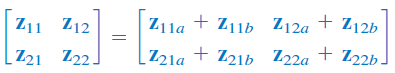
یا

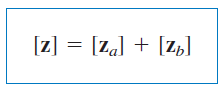
مشاهده می‌کنیم که پارامتر $$z$$ شبکه کلی، برابر با مجموع پارامترهای $$z$$ زیرشبکه‌های آن است. این گفته، برای $$n$$ دوقطبی سری صادق است. اگر شبکه‌ها با پارامتر $$h$$ بیان شده باشند، می‌توان با استفاده از جدول تبدیلاتی که در بالا آورده شد، ابتدا پارامترهای $$h$$ را به پارامترهای $$z$$‌ تبدیل، سپس آن‌ها را با یکدیگر جمع و درنهایت با استفاده از جدول تبدیلات، پارامترهای $$z$$ به‌دست آمده را به پارامترهای $$h$$‌ تبدیل کرد.

اتصال موازی

شبکه‌های دوقطبی وقتی با هم موازی هستند که ولتاژ دوسر آن‌ها برابر باشد و جریان شبکه حاصله، برابر با مجموع جریان آن‌ها باشد. شکل 12، اتصال موازی دو شبکه دوقطبی را نشان می‌دهد.

با توجه به شکل بالا، می‌توان روابط زیر را نوشت:

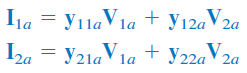
و

همچنین، روابط بین جریان و ولتاژها به‌صورت زیر است:

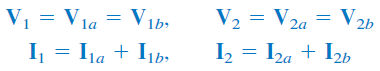
با جایگذاری روابط، می‌توان نوشت:

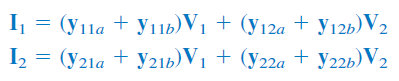
بنابراین، برای پارامترهای $$y$$ شبکه کلی داریم:

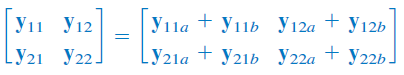
یا

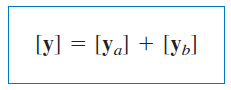
می‌بینیم که پارامترهای $$y$$ شبکه کلی، برابر با مجموع پارامترهای $$y$$ هر یک از دوقطبی‌های آن است. این گفته را می‌توان به $$n$$ دوقطبی موازی تعمیم داد.

اتصال متوالی

دو شبکه را متوالی گوییم، اگر خروجی یکی، ورودی دیگری باشد. شکل 13، اتصال متوالی دو شبکه دوقطبی را نشان می‌دهد.

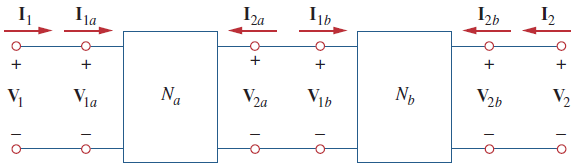
برای هریک از دوقطبی‌ها، روابط زیر را داریم:

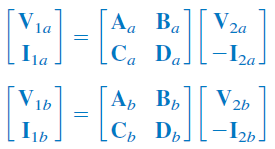
با توجه به روابط پارامترهای انتقال شبکه نیز می‌توان روابط زیر را نوشت:

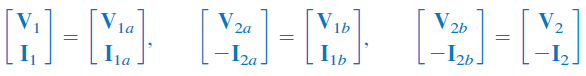
با جایگذاری پارامترهای انتقال هریک از دوقطبی‌های $$N_a$$ و $$N_b$$ در معادله اخیر، می‌توان رابطه حاکم بر شبکه کلی را به‌صورت زیر بیان کرد:

یا

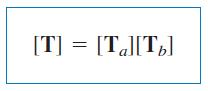
می‌بینیم که در یک شبکه متوالی از دوقطبی‌ها، پارامترهای انتقال شبکه برابر با ضرب پارامترهای انتقال دوقطبی‌ها است.

در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد می‌کنیم به آموزش‌ مراجعه کنید:

• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس

^^