تحلیل سری زمانی – تعریف و مفاهیم اولیه
تحلیل سری زمانی، در دهههای اخیر بسیاری از محققین را به سوی خود جذب کرده است. هدف اصلی در تحلیل سری زمانی در مورد یک پدیده، ایجاد یک مدل آماری برای دادههای وابسته به زمان براساس اطلاعات گذشته آن پدیده است. با این کار امکان پیشبینی در مورد آینده پدیده مورد بحث میسر میشود. به بیان دیگر تحلیل سری زمانی، ایجاد مدلی گذشتهنگر است تا امکان تصمیمات آیندهنگر را فراهم سازد. شما میتوانید نحوه اجرای تحلیلهای سری زمانی و دیگر تحلیلهای دینامیکی را با استفاده از فیلمهای مجموعه آموزش تحلیل دینامیکی – مقدماتی تا پیشرفته در فرادرس به سادگی یاد بگیرید.


ایجاد و به کارگیری مدلهای آماری و تصادفی در قالب تحلیل سری زمانی، امروزه به کمک رایانههای پرسرعت، بسیار فراگیر شده و حاصل آن مدلهایی است که با داشتن پارامترهای بسیار انعطافپذیر، میتوانند آینده را برای هر پدیدهای (در صورت وجود دادههای مناسب در گذشته) پیشبینی کنند. کاربردهای تحلیل سریهای زمانی، در زمینههای مختلف نظیر، کسب و کار، امور مالی، بورس، مهندسی و ... دیده میشود.
سری زمانی (Time Series)
دنبالهای از دادهها که در یک محدود زمانی جمعآوری شدهاند، یک سری زمانی را تشکیل میدهند. این دادهها تغییراتی که پدیده در طول زمان دچار شده را منعکس میکنند. بنابراین میتوانیم این مقدارها را یک بردار وابسته به زمان بدانیم.
در این حالت اگر X یک بردار باشد، سری زمانی را میتوان به صورت زیر نشان داد؛ که در آن t، بیانگر زمان و X نیز یک متغیر تصادفی است.
طبق این تعریف زمان t=0 نیز قابل تعریف است. این لحظه میتواند زمان تولد یک پدیده یا هنگامی باشد که اولین اطلاعات در آن لحظه ثبت شده است. به این ترتیب متغیر تصادفی X را در زمان t نشان میدهد. مقدارهای مشاهده شده این متغیر تصادفی دارای ترتیبی هستند که زمان وقوع هر داده را نشان میدهند.
اگر متغیر تصادفی X، یک بعدی باشد، یعنی از بین ویژگیهای مختلف یک پدیده فقط از یکی ویژگی برای ایجاد مدل سری زمانی استفاده شود، مدل را «یک متغیره» (Univariate) مینامند. ولی اگر از چندین ویژگی برای ایجاد مدل سری زمانی استفاده شود، مدل سری زمانی را «چند متغیره» (Multivariate) میگویند. البته اگر علاوه بر زمان، مکان یا مختصات را (یا هر اطلاعاتی که مقدار دادهها به آن وابسته باشند) به مدل اضافه کنیم، وارد مبحث «آمار فضایی» (Spatial Statistic) خواهیم شد.

همچنین اگر تغییرات پدیده را در مدل سری زمانی برای زمانهای منقطع در نظر بگیریم، سری را زمان-گسسته (Discreet Time) و برعکس اگر زمان را به صورت پیوسته در مدل فرض کنیم، سری را زمان-پیوسته (Continuous Time) مینامند. برای مثال ثبت دما، دبی رودخانه و ... از گروه سریهای زمان-پیوسته هستند و تعداد جمعیت، تولیدات کارخانه و ... از نوع سری زمان- گسسته محسوب میشوند.
معمولا در سری زمان-گسسته، دادهها در مقاطع مشخصی از زمان مثل ساعت، روز یا هفته و حتی سال جمعآوری میشوند. غالباً ایجاد مدلها برای سریهای زمان-گسسته انجام میشود زیرا با استفاده از گروهبندی و ایجاد فاصلههای زمانی ترتیبی، امکان تبدیل سریهای زمانی-پیوسته به زمان-گسسته وجود دارد.
مولفههای یک سری زمانی
معمولا میتوان الگوی رفتار یا مدل تغییرات یک سری زمانی را به چهار مولفه تفکیک کرد. «روند» (Trend)، «تناوب» (Cyclic)، «فصل» (Seasonal) و «تغییرات نامعمول» (Irregular). اگر نمودار مربوط به دادههای سری زمانی را برحسب زمان ترسیم کنیم میتوانیم این مولفهها را تشخیص دهیم در نتیجه شناخت بهتری از دادههای سری زمانی خواهیم داشت. در ادامه به معرفی و بررسی هر یک از این مولفهها میپردازیم.
- روند (Trend): تمایل سری زمانی به افزایش، کاهش یا حتی ثابت بودن، روند را تشکیل میدهد. در یک سری زمانی با روند افزایشی، انتظار داریم مقدارهای سری زمانی در زمانهای و به صورت باشند. برای مثال روند برای سری زمانی مربوط به میزان جمعیت یا سرمایه در بازار بورس به صورت افزایشی، ولی روند برای میزان مرگ و میر با توجه به پیشرفت در امور پزشکی، کاهشی است.
در تصویرهای زیر سه نمودار مربوط به سه سری زمانی در ۱۰۰ زمان مختلف با روندهای افزایشی، ثابت و کاهشی نشان داده شده است.
| روند کاهشی | روند ثابت | روند افزایشی |
 |  |  |
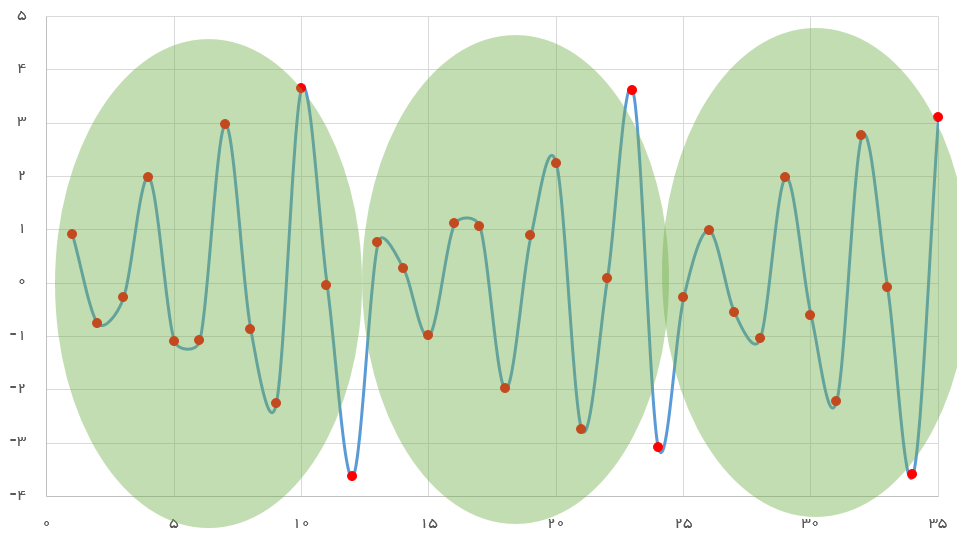
تناوب (Cyclic): تغییرات یکسان و تکراری در مقاطع میانمدت، تناوب در سری زمانی نامیده میشود. معمولا این تناوب ممکن است هر دو سال یا بیشتر اتفاق بیافتد. برای مثال تناوب در کسب و کار دارای یک چرخه چهار مرحلهای است که باعث میشود دادههای مربوط به کسب و کار در یک دوره تناوب 3 ساله تکرار شوند. 
- فصل (Seasonal): در سری زمانی، تغییراتی که در دورهای کوتاهتر از یک تناوب به صورت تکراری رخ میدهد، به تغییرات فصلی معروف است. برای مثال در طول یک سال میزان فروش لباسهای گرم در زمستان افزایش داشته و سپس در فصلهای دیگر کاهش داشته است. این تناوب در سالهای بعد نیز به همین شکل تکرار میشود. همانطور که مشخص است دوره تکرار تغییرات فصلی کوتاهتر از دوره تکرار برای تغییرات تناوبی است.
- تغییرات نامعمول (ّIrregular): این گونه تغییرات بر اثر عوامل تصادفی و غیرقابل پیشبینی ایجاد میشوند. برای مثال زلزله یا سیل در بررسی رشد جمعیت ممکن است اثرات بزرگی داشته باشد. این مولفه بعد از شناسایی توسط نمودار ترسیم شده از سری زمانی باید حذف شود. در غیر اینصورت نتایج حاصل از تحلیل سری زمانی ممکن است گمراه کننده باشند.

مدلهای سری زمانی
نحوه ارتباط و اثراتی که مولفههای گفته شده در سری زمانی دارند، مدل سری زمانی را تعیین میکند. معمولا دو شکل برای ارتباط این مولفهها در نظر گرفته میشود. اگر مقدار سری زمانی باشد و اثر مولفه روند، اثر مولفه تناوب، اثر مولفه فصل و نیز اثر مولفه تصادفی باشد، میتوان این دو مدل سری زمانی را به صورت زیر معرفی کرد:
«مدل ضربی» (Multiplicative Model): با فرض اثر متقابل هر مولفه بر مولفه دیگر، مدل به صورت است.
«مدل جمعی» (Additive Model): با فرض استقلال مولفهها با یکدیگر، مدل جمعی به صورت نوشته میشود.
این دو مدل نشان میدهند که هر مقدار از سری زمانی چگونه به چهار مولفه یاد شده مرتبط است. ولی اگر قرار باشد عمل پیشبینی برای سری زمانی انجام شود، باید به دنبال رابطه بین مقدارهای سری باشیم. که در بحث تحلیل سری زمانی بررسی میشود.
سری زمانی ایستا
هنگامی امکان پیشبینی برای سری زمانی وجود دارد، که به صورت «ایستا» (Stationary) در آمده باشد. منظور از یک سری زمانی ایستا، دنبالهای از مقادیر وابسته به زمان است که میانگین و واریانس آن به زمان وابسته نباشند. در حقیقت در یک سری زمانی ایستا، قوانین حاکم بر تغییرات مقدارها، وابسته به زمان نیست.
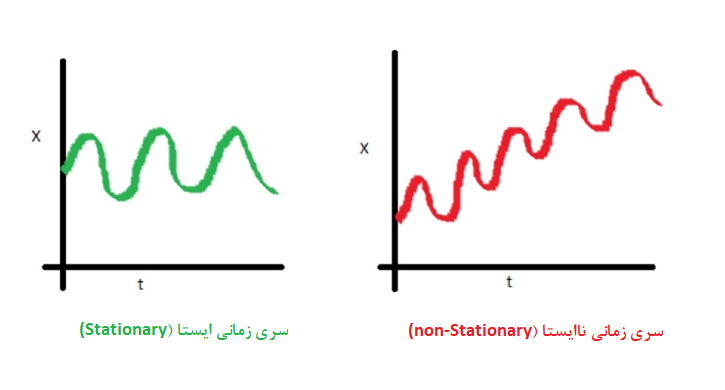
پس ابتدا باید مولفههایی مانند روند یا تغییرات فصلی را از سری زمانی خارج کرد تا سری زمانی تبدیل به یک سری ایستا شده و امکان پیشبینی و مدل سازی بوجود آید. عملگرهای «میانگین متحرک» (Moving Average)، تفاضلگیری (Difference) و تبدیلات توانی روشهایی هستند که به ایستایی سری زمانی کمک میکنند.
روشهای ایستا کردن سری زمانی
از آنجایی که امکان پیشبینی برای سریهای زمانی ناایستا (Non-stationary) به راحتی امکان پذیر نیست، بهتر است عواملی که باعث خارج شدن سری زمانی از حالت ایستایی هستند، حذف شوند. به این ترتیب باید مولفههای شناسایی شده در سری زمانی را حذف کنیم. به این کار «هموار سازی» (Smoothing) یا «صافی» (Filtering) میگویند. روشهای مختلفی برای هموارسازی سری زمانی وجود دارد. عملگرهای میانگین متحرک، هموارسازی نمایی ساده، روشهای تفاضلگیری و ... به حذف مولفههای سری زمانی کمک میکنند. در این نوشتار به بررسی عملگر میانگین متحرک پرداخته و نقش آن را در حذف مولفه روند بررسی و سپس سری زمانی ایستای تولید شده را، تحلیل میکنیم.
عملگر میانگین متحرک
عملگر میانگین متحرک با توجه به درجه انتخابی برای میانگینگیری مثلا k، هر مقدار از سری زمانی را با میانگین k-1 مقدار قبلی و خودش جایگزین میکند. این کار به حذف روند و تشکیل الگوی ساده برای سری زمانی کمک بسیاری میکند. میانگین متحرک یک روش هموارسازی دادهها است. البته این عملگر، مولفه روند را برای سری زمانی برآورد میکند تا در زمان پیشبینی از آن استفاده شود.
مثال ۱
فرض کنید یک سری زمانی طبق جدول زیر برای ۱۰ زمان مختلف ثبت شده است. اگر درجه هموار سازی میانگین متحرک را برابر با ۳ در نظر بگیریم، باید میانگین مقدار جاری و دو مقدار قبلی (مجموعه سه مقدار) را بدست آوریم و جایگزین مقدار جاری کنیم.
| زمان | مقدار سری زمانی | همواره سازی بامرتبه 3 | سری زمانی بدون روند با میانگین متحرک مرتبه ۳ | همواره سازی با مرتبه 5 | سری زمانی بدون روند با میانگین متحرک مرتبه ۵ |
| 0 | 10 | - | - | - | - |
| 1 | 12 | - | - | - | - |
| 2 | 14 | 12 | 2 | - | - |
| 3 | 15 | 13.67 | 1.33 | - | - |
| 4 | 17 | 15.33 | 1.67 | 13.6 | 3.4 |
| 5 | 17 | 16.33 | 1.67 | 15 | 2 |
| 6 | 19 | 17.67 | 1.33 | 16.4 | 2.6 |
| 7 | 22 | 19.33 | 2.67 | 18 | 4 |
| 8 | 23 | 21.33 | 1.67 | 19.6 | 3.4 |
| 9 | 28 | 24.33 | 3.67 | 21.8 | 6.2 |
واضح است که برای دو مقدار اول در سری زمانی، این کار امکان پذیر نیست زیرا نمیتوان سه مقدار برای محاسبه میانگین در نظر گرفت. در نتیجه این گونه هموار سازی به کاهش مجموعه داده منجر میشود. هر چه درجه همواره سازی را بزرگتر انتخاب کنید، هموارسازی زودتر انجام خواهد شد ولی در عوض ممکن است خطای پیشبینی را افزایش دهد.
حال برای آنکه سری زمانی، خاصیت ایستایی پیدا کند و روند را از آن حذف کنیم، کافی است مقدارهای سری زمانی را از میانگین متحرک کم کنیم، سری زمانی جدید بدون روند خواهد بود. پس اگر سری زمانی باشد و میانگین متحرک در زمان t در نظر گرفته شود، سری زمانی ایستای به صورت زیر مورد محاسبه قرار میگیرد.
به تصویرهای زیر دقت کنید. در سمت راست نمودار سری زمانی به همراه مقدارهای حاصل از عملگرهای میانگین متحرک مرتبه ۳ و ۵ دیده میشود. همچنین در سمت راست سری زمانی ناایستا به رنگ آبی و سریهای زمانی ایستای حاصل از عملگر میانگین متحرک مرتبه ۳ و ۵ به رنگهای بنفش و سبز نمایش داده شدهاند. کاملا مشخص است که در سریهای زمانی ایستای تولید شده، مولفه روند وجود ندارد.
| سری زمانی و نتیجه عملگر میانگین متحرک مرتبه ۳ و ۵ | سری زمانی اصلی و سری زمانی ایستا براساس عملگر میانگین متحرک مرتبه ۳ و ۵ |
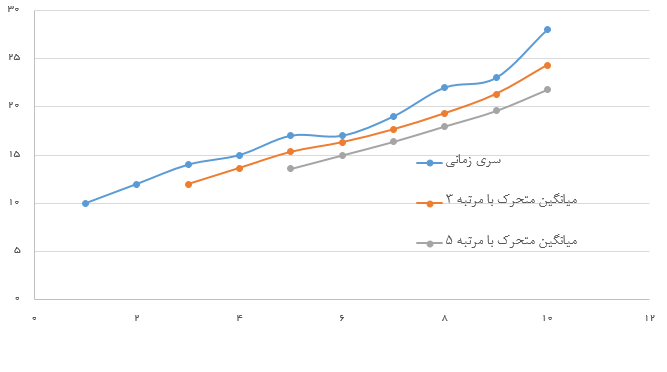 | 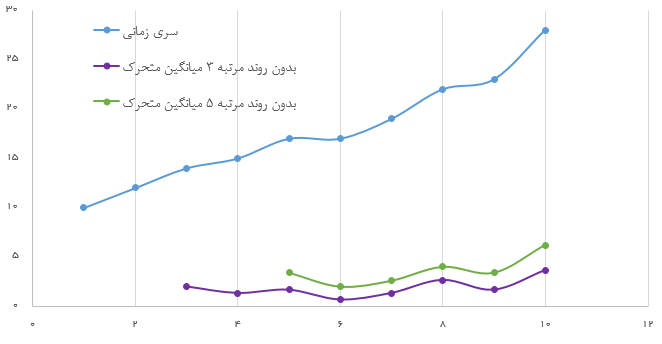 |
برای مشاهده واضحتر و دقیق سری زمانی سمت راست، روی این لینک و مشاهده سری زمانی سمت چپ، روی این لینک کلیک کنید.
تحلیل سری زمانی
بعد از شناسایی و حذف مولفههای اصلی سری زمانی، وقت آن رسیده که بتوانیم عمل پیشبینی را انجام دهیم، یعنی مدل ریاضی برای ارتباط بین مقدارهای سری زمانی را پیدا کنیم. در اینجا به دو مدل پیشبینی سری زمانی به نام «میانگین متحرک» (Moving Average) و «اوتورگرسیو» (Autoregressive) میپردازیم.
روش پیشبینی میانگین متحرک
برای پیشبینی سری زمانی ایستا که روند از آن خارج شده است، میتوان از مدل میانگین متحرک استفاده کرد. در این مدل سری زمانی به صورت زیر نوشته میشود:
که در آن همان خطای تصادفی با میانگین صفر و واریانس ثابت است. به این مدل، میانگین متحرک مرتبه q گفته و به صورت نمایش داده میشود. در این مدل مقدار سری زمانی در زمان t یک ترکیب خطی از خطاها تا زمان t است.
با توجه به تعریف مدل و صفر بودن میانگین ، مشخص است که میانگین سری زمانی ایستا برابر است با . برای محاسبات راحتتر در مدل، میتوان این میانگین را از سری زمانی ایستا کم کرد تا مدل به صورت زیر نوشته شود، که در آن و پارامترهای مدل هستند.
استفاده از این مدل باید با در نظر گرفتن یک شرط صورت پذیرد. شرطی که در این مدل باید رعایت شود، آن است که میبایست قدرمطلق ضرایب مدل کوچکتر از یک باشند.
مدل میانگین متحرک درجه ۱ به صورت زیر نوشته میشود:
اگر میزان خطا را برای زمان t به صورت نشان دهیم، خواهیم داشت.
به این ترتیب میتوان بوسیله کمینهسازی مقدار مربعات خطا، پارامتر مدل را برآورد کرد. بنابراین با رعایت شرط مربوط به مدل، بوسیله الگوریتمهای بهینهسازی، مقدار پارامترهای مدل در مثال ۱ را برآورد میکنیم. توجه داشته باشید که میانگین سری زمانی که برابر با 2.001 است، برای تحلیل، از همه مقدارها کم شده.
مجموع مربعات خطا در این مدل به صورت زیر است:
باید توجه کرد که در زمان صفر نمیتوان خطا را اندازه گرفت در نتیجه محاسبه خطا و مقدار سری زمانی براساس مثال ۱ از زمان یک محاسبه شده و در جدول زیر دیده میشود. توجه داشته باشید که میزان خطا بعد از برآورد پارامتر محاسبه شده است. ولی ابتدا با فرض صفر بودن پارامتر به عنوان حدس اولیه میتوان روند کمینهسازی مربعات خطا را آغاز کرد.
| زمان | به علت هموارسازی میانگین متحرک مرتبه ۳، دو مقدار اول حذف شدهاند. | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| سری زمانی | 0.1250 | -0.5417 | -0.2083 | -1.2083 | -0.5417 | 0.7917 | -0.2083 | 1.7917 | |
| میزان خطا | 0.1250 | -0.5413 | -0.2099 | -1.2089 | -0.5452 | 0.7901 | -0.2060 | 1.7911 |
با استفاده از روش بهینه سازی، برآورد پارامتر خواهد بود که البته مربعات خطا نیز بدست میآید.
حال با استفاده از پارامتر مدل میتوان پیشبینی را برای مشاهده زمان t=10 انجام داد. کافی است که براساس مدل مقدار سری زمانی ایستا را در زمان t=10 بدست آورد سپس میانگین سری را به آن افزود. در آخر نیز باید روند به مقدار پیشبینی شده اضافه شود. نتیجه محاسبات در ادامه قابل رویت است:
روش پیشبینی اتورگرسیو
اگر مقدارهای سری زمانی ایستا به صورتی باشند که به مقدارهای قبلی خود بستگی داشته باشند، از مدل اتورگرسیو استفاده میشود. در این حالت p را تعداد مشاهدات گذشته در نظر میگیریم که برای پیشبینی یک مقدار در نظر گرفته میشود. بنابراین میتوانیم مدل اتورگرسیو را برای سری زمانی ایستا به صورت زیر بنویسیم:
در این رابطه پارامترهای مدل اتورگرسیو و خطای تصادفی در نظر گرفته میشود. چنین مدلی را به صورت نشان میدهند و p را مرتبه مدل مینامند. انتخاب مقدار p نیاز به بررسی سری زمانی و میزان همبستگی مقدارهای سری زمانی به یکدیگر دارد.
از آنجایی که این مدل به مانند یک مدل رگرسیون نوشته شده، به آن مدل اتورگرسیو میگویند، با توجه به اینکه برای رگرسیون روی مقدارهای گذشته ایجاد شده، شرط استقلال متغیرهای توصیفی حداقل برای تعداد دستههای کوچکتر از p وجود نخواهد داشت. همچنین مقدار حال حاضر سری زمانی فقط به p مقدار قبلی وابسته بوده و به قبل از آن ارتباطی ندارد.
معمولا برای بررسی سری زمانی ایستا از مدل اتورگرسیو مرتبه اول یا دوم استفاده میشود. مدل اتورگرسیو مرتبه اول به صورت زیر است:
حال برای بدست آوردن ضریب و کافی است که رگرسیون حاصل از مقدارهای را روی بدست آوریم. توجه داریم که در این حالت، روی سری زمانی ایستا محاسبات باید انجام بپذیرد. برای این کار کافی است در مثال ۱ دادهها را بر طبق جدول زیر مرتب کنیم. (زمان ۰ تا ۱) به دلیل محاسبات میانگین متحرک مرتبه ۳ وجود ندارند.
| زمان | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| X(t-۱) | 2 | 1.333 | 1.667 | 0.667 | 1.333 | 2.667 | 1.667 |
| X(t) | 1.333 | 1.667 | 0.667 | 1.333 | 2.667 | 1.667 | - |
به این ترتیب ضرایب رگرسیون برابر خواهد بود با و در نتیجه مدل اتورگرسیو با این ضرایب به صورت نوشته میشود.
بر اساس این رابطه میتوان سری زمانی را برای زمان t=10 پیشبینی کرد. کافی است با توجه به رابطهای که بین و داشتیم، مقدار روند برای زمان را محاسبه کرده و به اضافه کنیم.
روش پیشبینی میانگین متحرک-اتورگرسیو
با توجه به خصوصیات هر یک از روشهای میانگین متحرک و اتورگرسیو، امکان ترکیب این دو روش نیز وجود دارد. چنین مدلی به نام میانگین متحرک-اتورگرسیو معروف است و در چنین حالتی مدل را به صورت نشان میدهند. رابطه بین مقدارهای سری زمانی ایستا در این مدل به صورت زیر قابل مشاهده است:
با توجه به این موضوع مدل به صورت زیر در خواهد آمد:
برای برآورد پارامترهای این مدل احتیاج است که با مباحث مربوط به تابع خودهمبستگی (Auto-correlation) و تابع خودهمبستگی جزئی (Partial Auto-correlation) آشنا باشید. همچنین رسم نمودارهای مربوط به این توابع همبستگی، برای تشخیص و انتخاب مدل مناسب راهگشا است.













آقای دکتر؛ سلام و عرض ارادت دارم محضر مبارک شما، خداوند برای شما خیرو و عزت دهد با این خدمات آموزشی عالی شما، درسهای شما خیلی عالی است. دست مریزاد. در ضمن من درسهای تحلیل سری زمانی خریداری کردم، اما فصل مربوط به داده های واقعی را که تدریس نمودید اون بخش اوتلایرها یا همان دادههای پرت را باز نمی کند، نمیدانم دلیلش چیست، خیلی مساله مهم نیز هست برایم. از لطف خود همین مشکل را برطرف نمایید، برمن منت می گذارید. با اداء احترام
با سلام؛
این مورد را میتوانید با با پشتیبانی فرادرس حتی به صورت آنلاین بررسی کنید.
با تشکر از همراهی شما با مجله فرادرس
با سلام خدمت استاد ری بد عزیز
من هواشناس هستم. چگونه تشخیص بدیم مدل سری زمانی ما مدل ضربی هست یا جمعی
با سپاس
سلام روز خوش
آیا می توان متغیرهای کیفی را در محاسبات لحاظ کرد؟ ( وقتی اثر چند متغیر را می خواهیم روی یک متغیر حساب کنیم؟)
ممنون، بسیار عالی توضیح داده شده بود.
سلام
تمام مطالبی که آقای دکتر ریبد آموزش میدن عالی هست
فقط اگر من درست متوجه شده باشم در روش میانگین متحرک، میانگین داده ها سری زمانی(ستون چهارم)2.001 است که در متن 1.875 محاسبه شده
نکته دوم هم حتی اگر این مقدار از داده ها کم بشه هم مقادیر ردیف اول از جدول دوم حاصل نمیشه
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در متن انجام شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام استاد سپاس از مطالب مختصر و مفیدتون ببخشید کتاب در مورد سریهای زمانی معرفی میکنید؟
سپاس . رشته من اقتصاد است و مطالب برای من بسیار قابل فهم بود .
با سلام و احترام
ضمن تشکر از انتشار مطالب خوب و مفیدتون
امکانش هست توضیح مختصری درباره روش پیشبینی LSTM نیز بفرمایید ؟؟
باتشکر
با سلام خدمت استاد محترم و تشکر از مطالب جامع و مفیدی که ارائه دادین.
یه خواهش داشتم و اینکه اگر ممکنه راجب مدل سری زمانی CARMA هم مطالبی رو ارائه بفرمایید.
با تشکر از توجهتون
سلام وقت بخیر
رشته من معماریه و دارم روی متغیر هایی از دید در یک مسیر مشخص در فضای معماری کار می کنم، این مسیر به 43 نقطه تقسیم شده و در هر نقطه این متغیر ها محاسبه شده. در حال حاضر داده های به دست آمده در هر نقطه رو نسبت به کل مسیر میخوام تحلیل کنم ( توالی داده ها اهمیت دارد) چه آزمون آماری مناسب هست؟ سری زمانی در این تحلیل کاربردی هست؟
سوال: جناب آقای دکتر ری بد عزیز، با تشکر از متن مفید و آموزنده شما، در این متن من دو مطلب را درست متوجه نشدم، ممنون میشوم اگر بتوانید پاسخ سوالتم را بدهید:
1- اگر درست متوجه شده باشم برای مدل سازی یک سری زمانی ایستا با روش MA، مفهوم روش این است که ما سری زمانی را ترکیب خطی از خطاها در نظر بگیریم. خطای بین پیش بینی مدل و مقدار واقعی. اما در این روش به چه روش تخمین انجام میشود؟ و چرا اسم این روش تخمین میانگین متحرک نامگذاری شده است؟ در صورتی که میانگین متحرک در مرحله قبل محاسبه و از سری زمانی حذف میشود و این مقدار در تخمین و مدل سازی سری زمانی نقشی ندارد.
2- در روش پیشبینی میانگین متحرک برای مثال 1، مقادیر درج شده در هر دو ردیف جدول یکسان هستند و من متوجه نشدم شما چطور آن مقادیر را محاسبه کرده اید. در صورت امکان برای چند زمان محاسبات را درج بفرمائید.
با تشکر فراوان
سلام وعرض ادب خدمت شما استاد بزرگوار و مجموعه مفیدتون
مطالب بسیار کمک کننده بود برام و بینهایت آرزوی خیر میکنم براتون.
برای محاسبه فرونشست چند نوع سری زمانی هست و بهترینشون و جدیترین سزی زمانی کدوم است؟
برای محاسبه فرونشست سری زمانی نمی توان خیلی مدلسازی کرد بلکه باید از پکیج ساب سیدنس در GMS استفاده کنید.
با سلام و احترام.
من میخواهم مصرف انرژی چند شهر را برای چند سال آینده و به تفکیک بخشهای مصرفکننده پیشبینی کنم؛ یعنی برای هرشهر ،به طور جداگانه، مصرف انرژی را در هر یک از بخشها پیشبینی کنم؛ برای این کار فقط آمار مصرف انرژی سالهای گذشته را دارم؛ آیا با پانل دیتا در ایویوز میتوان این کار را انجام داد؟ لطفاً راهنمایی بفرمایید. باسپاس.
ممنونم
سلام آقای ری بد
امکانش هست در خصوص محاسبه میزان خطا و تتا در روش میانگین متحرک یک توضیح مختصر ارائه بفرمائید؟
سلام و عرض ادب
بسیار مطالب مفیدی ارائه کردید، سپاسگذارم.
اقای دکتر یک سوال، اگر مثلا برای پیش بینی تولید برنج، علاوه بر داده های تولید برنج، متوسط بارش و متوسط رطوبت خاک را هم در نظر بگیرم، از چه مدلی از سری زمانی باید استفاده کنم؟ ممنون میشم مرا راهنمایی بفرمایید.. سپاسگذارم
درود،
خوشحالیم که این نوشتار توجه شما را جلب کرده است.
همانطور که گفته شد، سری زمانی ابتدا باید به یک سری ایستا (با میانگین و واریانس ثابت) تبدیل شود. به این ترتیب، روند از آن حذف شده، و بعد از اینکه مدل و پارامترها، برازش شد، این میانگین یا روند به آن اضافه خواهد شد.
برای اشنایی بیشتر از نحوه به کارگیری سری زمانی بهتر است نوشتارهای دیگر مجله فرادرس که با این موضوع مرتبط هستند مانند تحلیل سری زمانی با پایتون — مقدمات و مفاهیم اولیه و سری زمانی در علم داده — از صفر تا صد را مطالعه کنید.
تندرست و سلامت باشید.
با سلام و تشکر از توضیحات کاملتون. یک سوال داشتم. اینکه برای ایستا کردن میانگین از تفاضلی کردن استفاده میشه ، متفاوت است با روش moving average؟ آیا برتری در این روش ها وجود دارد؟
سلام و درود،
همانطور که در متن نیز اشاره شد، تفاضلی کردن روشی برای حذف ترند و ایستا کردن سری زمانی است. در حالیکه میانگین متحرک، یک مدل برای سری زمانی ارائه میکند به شرطی که روند در آن وجود نداشته باشد. بنابراین اولی پیشنیاز برای دومی است.
تندرست و پیروز باشید.
سلام و خسته نباشید. ممنون از مطلب خوبتون. اگر که امکانش هست میشه توضیح بدید که میزان خطا از کدوم فرمول محاسبه میشه؟ مثلا مقدار -0.5413 چیجوری محاسبه شده؟
سلام میشه درمورد تاخیر زمانی هم توضیحی بدید متشکرم
با سلام
سري تبدیل یافته با پیش بینی برای چند دوره بعد را چجوری به سری اولیه داده ها تبدیل کنیم؟ ممنون می شوم روش عکس را توضیح بدید برام برای رسیدن به داده های اولیه/…
با سلام و احترام و عرض خداقوت
من به خاطر موضوع پایان نامه چند روزی است درگیر خواندن مفاهیم سری زمانی شده ام، کل هفته گذشته رو از روی چند کتابی که در این زمینه خریداری کرده بودم، مطالب رو مطالعه میکردم، واقعا گیج کننده بود.
من مشتری چند ساله فرادرس هستم، آموزش های قبلی شما را در قالب ویدئو دیده بودم، ولی در اینجا واقعا شیوه ساده و کامل بیان مطالب و تسلط شما برای بنده حیرت انگیز بود. اینکه با یک متن چند خطی، کلیات مفاهیم سری زمانی اینقدر کامل در ذهنم نشست، خیلی خوب بود، واقعا از شما و فرادرس ممنونم. عالی هستید. ان شاءالله در همه امور زندگی موفق باشید.
سلام و با تشکر از مطالب آموزنده شما. در مورد روش های تحلیل و مدل های سری زمانی شما صفحه آموزش مختلف در این وب سایت دارین به طوری که بعضی از مفاهیم را چندین مرتبه و بصورت کاملا متفاوت مطرح کردین. برای مثال روش Moving Average در اینجا کاملا متفاوت است با توضیح همین روش در “سری زمانی در علم داده — از صفر تا صد” که این کمی گیج کننده ست. لطفا توضیح بدین که این روش بالاخره برای پیش بینی یک سری زمانی به چه صورتی باید استفاده بشه. به صورت ترکیب خطی از خطاها تا زمان t یا بصورت مقدار پیشبینی برای زمان بعدی به صورت میانگین مقدارهای قبلی خواهد بود؟ پیشاپیش ممنونم.
سلام و درود بر شما خواننده گرامی!
به یاد داشته باشید که روش میانگین متحرک، یک روش برای از بین بردن روند در سری زمانی است. از طرفی مدل میانگین متحرک یک مدل سری زمانی نیز هست. در حقیقت به دو شیوه از میانگین متحرک یاد میشود. در یک جا با توجه به عملگر میانگین متحرک، روند را از بین برده و در جای دیگر برای ایجاد مدل سری زمانی با مدل میانگین متحرک (MA) به کار میرود.
پس در حقیقت این دو، مفاهیم جداگانه و البته مرتبط با یکدیگر هستند.
از اینکه همراه مجله فرادرس هستید بسیار سپاسگزاریم.
شاد و تندرست باشید.
سلام
سپاسگزارم بابت مطالب آموزنده ای که در اختیار عموم قرار دادید.
اگر امکانش هست لطفا منابع مطالب رو هم ذکر بفرمایید.
سلام و درود
از اینکه همراه مجله فرادرس هستید بسیار خوشحالیم!
در همه کتابهای سریهای زمانی این مباحث دیده میشود. میتوانید برای مثال به کتاب پیش بینی سری های زمانی: از مقدماتی تا پیشرفته به همراه برنامه کاربردی در R انتشارات دانشگاه امیرکبیر مراجعه کنید.
شاد و سلامت و پیروز باشید.
بی نهایت از وقتی که گذاشتید و توجهون ممنونم
موفق باشید
با سلام
بابت پاسخگویی و بذل توجه حضرتعالی ممنون و سپاسگزارم
سؤال پایانی بنده اینه که چه میزان خطا این نوع پیشگویی به داده ها وارد میکند و دیگر اینکه آیا روش های داینامیک هم برای پیشگویی وجود دارند یا صرفا تنها روش پیشگویی سری های زمانی به صورت ایستا کردن داده ها می باشد؟
با تشکر
با سلام و وقت بخیر
از اینکه همراه مطالب فرادرس هستید بسیار سپاسگزاریم
بله همانطور که اشاره کردید، روشهای پویا برای تحلیلهای چند متغیره نیز وجود دارد.
مدل های خطی پویا (DLM) یک چارچوب بسیار عمومی برای تجزیه و تحلیل داده های سری زمانی ارائه می دهند. بسیاری از مدل های سری زمانی کلاسیک را می توان به عنوان DLM تعریف کرد ، از جمله مدل های ARMA و مدل های رگرسیون خطی چندگانه می توانند به عنوان مدلهای رگرسیون عادی در نظر گرفته شوند که ضرایب در زمان متفاوت باشند.
اگر در اینترنت جستجو کنید روشهای شبکههای بیزی نیز در این زمینه به کار گرفته میشوند.
از اینکه خواننده نوشتههای مجله فرادرس هستید خوشحالیم!
موفق باشید
با سلام و عرض خسته نباشید بابت مطالب روان و مفید بلاگ
یک سؤال دارم:
آیا ایستا کردن سری زمانی (حذف روند، تناوب و …) در سری هایی مانند داده های مالی و بورسی که عمدتا روند دار هستند، باعث مختل شدن پیش بینی مقادیر این سری ها در آینده و افزایش خطا نمی شود؟
پیشاپیش از بذل توجه شما سپاسگزارم
با سلام و تشکر از همراهی شما با مجله فرادرس
همانطور که فرمودید، ایستا کردن سری زمانی کمک به پیشگویی آن میکند. پس از اعمال پیشگویی میتوان روندی که حذف شده را به دادهها اضافه کرد تا نتایج برای کار قابل استفاده باشند. در نوشتاری که خواندهاید مثالهایی وجود دارد که پس از پبشبینی روند را به سری زمانی اضافه کرده است.
از اینکه به مجله فرادرس توجه دارید سپاسگزاریم- موفق باشید
بسیار عالی بود
سوالی که داشتم اینه که ضرایب تتا و میزان خطا در روش میانگین متحرک چه جوری محاسبه شده اند؟
خیلی ممنون
مفید بود ضمن این که واقعا منابع فارسی واقغا کم هستن
با سلام و عرض ارادت
موقعیکه دروس و مطالب شما را می بینم بشدت احساس غبطه بهم دست میده میگم کاش میشد از اول ترم مطالب زیبای شما را مطالعه می کردم….
مطالب ارایه شده کاملا پیوسته ، گویا ، روان نگاشته شده …
به شما خسته نباشید میگم، متشکرم
با سلام و خسته نباشید خمت استاد محترم مطالب عالی بود متشکرم
خیلی مفید بود، ممنونم
فقط تو دو تا از جدول ها چند تا عدد اشتباه نوشته شدن.
با سلام و سپاس از توجه شما به وبلاگ فرادرس!
اصلاحات در جدول مورد نظر انجام شد. با تشکر مجدد از شما که همراه فرادرس هستید.