مساله سفر اسب – به زبان ساده
در این مطلب، روش حل مساله سفر اسب بیان و پیادهسازی راهکار ارائه شده، در زبانهای برنامهنویسی گوناگون انجام شده است. «پسگرد» (Backtracking) یک پارادایم الگوریتم است که راهکارهای مختلف را تا هنگامی امتحان میکند که راه حل مساله پیدا شود. مسائلی که با استفاده از روشهای پسگرد حل میشوند، دارای خصوصیات مشابهی هستند که در ادامه بیان شده است. این مسائل تنها با آزمودن کلیه پیکربندیهای ممکن، قابل حل هستند و هر پیکربندی تنها یکبار بررسی میشود. یک راهکار ساده برای این مساله، آزمودن همه پیکربندیها و خروجی دادن پیکربندی است که از محدودیتهای مسأله داده شده پیروی میکند.
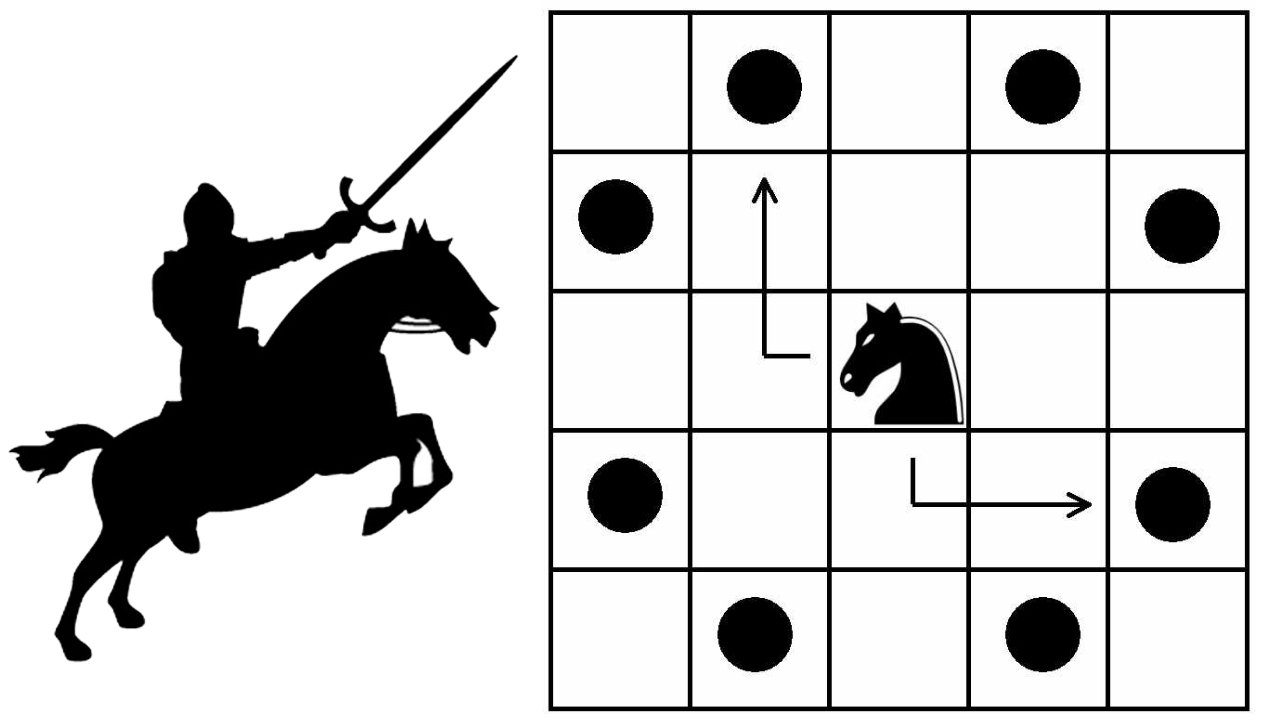
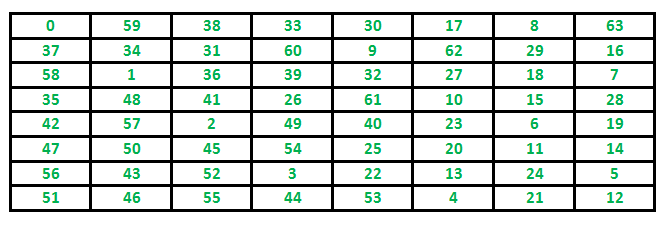
پسگرد به شیوه افزایشی کار میکند و یک بهینهسازی برای راهکار ساده (Naive Solution) است که همه پیکربندیهای ممکن را تولید و بررسی میکند. برای مثال، میتوان مساله سفر اسب را در نظر گرفت. اسب در اولین بلوک از یک تخته خالی قرار میگیرد و بر اساس قوانین شطرنج باید از هر خانه فقط و فقط یکبار عبور کند. در ادامه، یک صفحه شطرنج ۸×۸ نشان داده شده است. اعداد داخل سلولها نشانگر شماره سفر اسب هستند.
ابتدا باید الگوریتم ساده و سپس الگوریتم پسگرد برای حل این مساله بررسی شود.
الگوریتم ساده برای مساله سفر اسب
در الگوریتم ساده، همه سفرها یکی یکی ساخته و از این جهت بررسی میشوند که آیا محدودیتها را ارضا میکنند یا خیر.
while there are untried tours
{
generate the next tour
if this tour covers all squares
{
print this path;
}
}
الگوریتم پسگرد برای مساله سفر اسب
الگوریتم پسگرد با به کارگیری یک راهکار افزایشی، اقدام به حل مساله سفر اسب میکند. به طور متداول، کار از یک بردار خالی آغاز میشود و عناصر یکی یکی اضافه میشوند. بدین معنا که عناصر از مسالهای به مساله دیگر متفاوت هستند. در مساله سفر اسب، حرکت اسب یک عنصر است.
هنگامی که یک عنصر اضافه میشود، بررسی خواهد شد که آیا عنصر کنونی محدودیتهای مساله را نقض میکند؟ اگر عنصر محدودیتهای مساله را نقض کند، این عنصر حذف و جایگزین دیگری آزموده میشود. اگر هیچ یک از جایگزینها کار نکردند، به گام پیشین رفته و عنصر اضافه شده در گام پیشین حذف میشود. اگر بازگشت به مرحله اول انجام شد، بدین معنا است که هیچ راه حلی وجود ندارد. اگر اضافه کردن یک عنصر محدودیتها را نقض نکند، عناصر به صورت بازگشتی یکی یکی اضافه میشوند. اگر بردار ویژگی کامل شد، راهکار در خروجی چاپ میشود.
الگوریتم پسگرد برای مساله سفر اسب
در ادامه، الگوریتم پسگرد برای مساله سفر اسب آورده شده است.
If all squares are visited print the solution Else a) Add one of the next moves to solution vector and recursively check if this move leads to a solution. (A Knight can make maximum eight moves. We choose one of the 8 moves in this step). b) If the move chosen in the above step doesn't lead to a solution then remove this move from the solution vector and try other alternative moves. c) If none of the alternatives work then return false (Returning false will remove the previously added item in recursion and if false is returned by the initial call of recursion then "no solution exists" )
در ادامه، پیادهسازی راهکار مسأله سفر اسب ارائه شده است. این برنامه یکی از راه حلهای ممکن مسأله را در شکل یک ماتریس دوبُعدی چاپ میکند. اساسا، خروجی یک ماتریس دوبُعدی و ۸×۸ با اعدادی از ۰ تا ۳۶ است و این اعداد گامهای برداشته شده توسط اسب را نشان میدهند.
برنامه حل مساله سفر اسب در C
برنامه حل مساله سفر اسب در جاوا
برنامه حل مساله سفر اسب در #C
برنامه حل مساله سفر اسب در پایتون
خروجی قطعه کدهای بالا به صورت زیر است.
0 59 38 33 30 17 8 63 37 34 31 60 9 62 29 16 58 1 36 39 32 27 18 7 35 48 41 26 61 10 15 28 42 57 2 49 40 23 6 19 47 50 45 54 25 20 11 14 56 43 52 3 22 13 24 5 51 46 55 44 53 4 21 12
شایان توجه است که روش پسگرد، بهترین راهکار برای حل مساله سفر اسب نیست و الگوریتمهای دیگری وجود دارند که در این مساله، دارای عملکرد بهتری هستند.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
- برنامه تشخیص وجود دور در گراف جهتدار — راهنمای کاربردی
- رنگآمیزی گراف به روش حریصانه — به زبان ساده
^^













مثل همیشه عالی