آزمون تی (T Test) در R — راهنمای کاربردی

یکی از روش‌های تجزیه و تحلیل آماری، استنباط آماری است که به واسطه اطلاعاتی که یک نمونه از جامعه آماری در اختیارمان می‌گذارد به یک تصمیم در مورد جامعه آماری می‌رسیم. آزمون‌های آماری مربوط به میانگین، مانند آزمون تی (T-test) یکی از انواع این روش‌ها است که در مورد میانگین جامعه آماری، دست به قضاوت می‌زند.

در این نوشتار به بررسی آزمون‌های تی (T-test) می‌پردازیم که آزمون‌های مربوط به برابری میانگین دو جامعه مستقل و یا برابری میانگین دو متغیر وابسته را تحلیل می‌کنند. برای انجام محاسبات نیز از زبان برنامه‌نویسی R استفاده کرده و با توابعی که این آزمون‌ را انجام می‌دهند، بیشتر آشنا خواهیم شد.

برای اطلاع بیشتر از اصطلاحاتی که در آزمون آماری به کار می‌رود بهتر است آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و آزمون فرض میانگین جامعه در آمار — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری نیز خالی از لطف نیست.

آزمون تی (T Test) در R

استنباط آماری هنر تصمیم‌گیری در مورد توزیع داده‌ها است. یک «تحلیل‌گر داده» (Data Scientist) با استفاده از تکنیک «آزمون فرض آماری» (Hypothesis Testing) دست به قضاوت زده و براساس داده‌های حاصل از نمونه، تصمیم می‌گیرد که یکی از فرض‌های، آزمون آماری را رد کند.

فیلم آموزش آزمون آماری و پی مقدار p-value در فرادرس

کلیک کنید

یکی از روش‌های آزمون فرض آماری در مورد میانگین جامعه، آزمون تی (T-test) یا آزمون تی استیودنت (T-student) است. معمولا در سه حالت از آزمون تی برای قضاوت در مورد میانگین استفاده می‌شود.

1. آزمون تی تک نمونه‌ای (One sample t test): آزمون در مورد برابری میانگین جامعه یا مقدار ثابت و معلوم مثل a.
2. آزمون تی دو جامعه مستقل (Two independent sample t test): آزمون در مورد برابری میانگین دو جامعه مستقل.
3. آزمون تی برای زوج‌ متغیرها (Paired sample t test): آزمون برابر میانگین دو متغیر از یک جامعه.

در همه این آزمون‌ها فرض نرمال بودن جامعه یا جامعه‌ها وجود دارد. همچنین ثابت بودن واریانس نیز برای هر سه حالت آزمون از فرض‌های اولیه است.

آزمون تی تک نمونه‌ای (One Sample T Test)

فرض کنید در یک جامعه نرمال می‌خواهیم میانگین جامعه را با یک مقدار مشخص ( که ممکن است تحلیل‌گر حدس زده است) مقایسه کنیم. اگر میانگین جامعه را $$mu$$ و مقدار حدس زده شده را با $$\mu_0$$ نشان دهیم، فرضیات یعنی «فرض صفر» (Null Hypothesis) و «فرض مقابل» یا «فرض مخالف» (Alternative Hypothesis) مربوط به آزمون تک نمونه‌ای به صورت زیر نوشته می‌شوند.

$$\large \begin{cases}H_0: \mu =\mu_0 \\H_1: \mu \neq \mu_0\end{cases}$$

بنابراین فرض صفر را به صورت «میانگین جامعه با مقدار $$\mu_0$$ برابر است» و فرض مقابل را به صورت «میانگین جامعه با مقدار $$\mu_0$$ برابر نیست» می‌خوانیم.

نکته: گاهی فرض مقابل ($$H_1$$) را به صورت $$H_A$$ نیز نشان می‌دهند.

البته در اینجا آزمون دو طرفه مورد نظر بوده است. «فرض صفر» (Null Hypothesis) یا $$H_0$$ بیان می‌کند که میانگین جامعه با مقدار حدسی برابر است در حالیکه «فرض مقابل» یا «فرض مخالف» (Alternative Hypothesis) نابرابری بین این دو مقدار را نشان می‌دهد.

برای انجام این آزمون در R، باید از تابع $$t.test()$$ استفاده کرد. پارامترهای این تابع در ادامه معرفی شده‌اند.

1t.test(x,
2       mu = 0, 
3arguments:
4- x : A vector to compute the one-sample t-test
5- mu: Mean of the population

آماره آزمون برای حالت تک نمونه‌ای به صورت زیر نوشته می‌شود:

$$\large T=\dfrac{\overline{x}-\mu_0}{\frac{s}{\sqrt{n}}}$$

در این جا، منظور از $$\overline{x}$$ میانگین نمونه، $$\mu_0$$ مقدار حدسی برای میانگین و $$s$$ انحراف استاندارد نمونه است. همچنین $$n$$ نیز تعداد نمونه را نشان می‌دهد.

آماره آزمون در این حالت دارای توزیع t با n-1 درجه آزادی است. یعنی داریم:

$$\large T\sim t(n-1)$$

بنابراین مقدار احتمال (p-value) را باید برحسب توزیع t بدست آورد. خوشبختانه تابع $$t.test()$$ این کار را انجام می‌دهد و براساس مقدار احتمال (p-value) و احتمال خطای نوع اول ($$\alpha$$) می‌توان در مورد رد فرض صفر تصمیم گرفت.

مثال ۱

یک کارخانه تولیدی کلوچه ادعا دارد که وزن هر کلوچه آن ۱۰ گرم است. یک نمونه ۳۰ تایی از این کلوچه‌ها تهیه و وزنشان اندازه‌گیری شده است. می‌خواهیم ادعای کارخانه را براساس این نمونه آزمون کنیم. در این حالت فرضیه‌ها به صورت زیر نوشته خواهند شد.

$$\large \begin{cases}H_0: \mu =10 \\H_1: \mu \neq 10\end{cases}$$

فایل اطلاعاتی مربوط به این داده‌ها را می‌توانید از اینجا دریافت کنید. کد زیر برای انجام این آزمون تهیه شده است.

1x=read.csv("sugar_cooki.csv")
2x
3t.test(x, mu = 10)

پس از اجرای این کد، خروجی به صورت زیر حاصل می‌شود. با توجه به مقدار احتمال (p-value) آزمون در سطح خطای $$\alpha=0.05$$ فرض صفر را رد نمی‌کند. زیرا مقدار احتمال (p-value=0.7944) از $$\alpha=0.05$$ بزرگتر است. پس این نمونه، دلیلی بر رد فرض صفر ارائه نمی‌دهد.

1> t.test(x, mu = 10)
2
3	One Sample t-test
4
5data:  x
6t = -0.26299, df = 29, p-value = 0.7944
7alternative hypothesis: true mean is not equal to 10
895 percent confidence interval:
9  9.979329 10.015961
10sample estimates:
11mean of x 
12 9.997645 
13
14>

البته در خروجی یک فاصله اطمینان Confidence Interval) ۹۵٪) نیز برای میانگین جامعه دیده می‌شود. کران‌های این فاصله اطمینان از 9.979329 تا 10.015961 است. باز هم از آنجایی این فاصله در برگیرنده مقدار ادعای کارخانه یعنی ۱۰ برای وزن هر کلوچه می‌باشد، می‌توان نتیجه گرفت که فرض صفر رد نخواهد شد. در انتهای خروجی نیز مقدار «میانگین نمونه‌ای» (Sample Mean) با مقدار 9.997645 دیده می‌شود.

آزمون تی دو نمونه‌ای مستقل (Two Independent Sample T Test)

در این حالت با دو جامعه مستقل مواجه هستیم و می‌خواهیم میانگین آن دو را با یکدیگر مقایسه کنیم. برای مثال فرض کنید که قرار است معاونت بهداشت دانشگاه در مورد وزن دانشجویان دختر و پسر قضاوت کند.

فیلم آموزش منوی Test نرم افزار آماری MedCalc (رایگان) در فرادرس

کلیک کنید

فرض بر این است که میانگین وزن دانشجویان دختر ($$\mu_A$$) از وزن دانشجویان پسر ($$\mu_B$$) کمتر است. براساس یک نمونه 9 تایی از دانشجویان دختر و یک نمونه ۱۲ تایی از دانشجویان پسر، قرار است آزمون تی با فرضیات زیر صورت بگیرد.

$$\large \begin{cases}H_0: \mu_A =\mu_B \\H_1: \mu_A \neq \mu_B\end{cases}$$

آماره آزمون در این حالت به صورت زیر نوشته خواهد شد.

$$\large T=\dfrac{\overline{x}_A-\overline{x}_B}{\sqrt{\frac{S^2}{n_A}+\frac{S^2}{n_B}}}$$

در اینجا منظور از $$S^2$$ واریانس آمیخته برای دو جامعه A و B است که به صورت زیر محاسبه می‌شود:

$$\large S^2=\dfrac{\sum_{i=1}^{n_{_A}}(X_i-\overline{X}_A)^2+\sum_{i=1}^{n_{_B}}(X_i-\overline{X}_B)^2}{n_1+n_2-2}$$

در این حالت آماره آزمون یعنی T دارای توزیع تی با $$n_A+n_b-2$$ درجه آزادی است.

نکته: از واریانس آمیخته زمانی می‌توان استفاده کرد که بتوان واریانس هر دو جامعه را یکسان در نظر گرفت. در غیر اینصورت آماره آزمون به صورت زیر نوشته می‌شود که به آماره «ولچ» (Weltch) معروف است.

$$\large T=\dfrac{\overline{x}_A-\overline{x}_B}{\sqrt{\frac{S_A^2}{n_A}+\frac{S_B^2}{n_B}}}$$

این آماره نیز دارای توزیع t با درجه آزادی زیر است:

 $$\large df=\dfrac{\Big(\frac{S_A^2}{n_{_A}}+\frac{S_B^2}{n_{_B}}\Big)^2}{\frac{S_A^4}{n^2_{_A}(n_{_A}-1)}+\frac{S_B^4}{n^2_{_B}(n_{_B}-1)}}$$

در این حالت تابع $$t.test()$$ را با پارامترهای بیشتری همراه خواهیم کرد. پارامترهای اولیه در جدول قبلی دیده می‌شود. در اینجا فقط به بررسی پارامترهای جدید می‌پردازیم.

1Arguments
2
3x:a (non-empty) numeric vector of data values.
4y: an optional (non-empty) numeric vector of data values.
5alternative: a character string specifying the alternative hypothesis, must be one of "two.sided" (default), "greater" or "less". You can specify just the initial letter.
6mu: a number indicating the true value of the mean (or difference in means if you are performing a two sample test).
7paired: a logical indicating whether you want a paired t-test.
8var.equal: a logical variable indicating whether to treat the two variances as being equal. If TRUE then the pooled variance is used to estimate the variance otherwise the Welch (or Satterthwaite) approximation to the degrees of freedom is used.
9conf.level: confidence level of the interval.

برای روشن شدن موضوع و نحوه استفاده از این پارامترها، در ادامه مثال‌هایی را برای انجام چنین آزمونی، مورد بررسی قرار می‌دهیم.

مثال ۲

اطلاعات مربوط به وزن 9 دانشجوی دختر و 12 دانشجوی پسر در جدول زیر آورده شده است.

با استفاده از آزمون تی دو نمونه‌ای، فرض برابری وزن این دو گروه را در مقابل فرض اینکه وزن دانشجویان دختر کمتر از پسران است، می‌سنجیم. اگر گروه دانشجویان دختر را با A و گروه دانشجویان پسر را با B نشان دهیم، آزمون فرض را باید برای فرض یکطرفه به شکل زیر نوشت، زیرا فرض مقابل به صورت رابطه «کمتر» نوشته شده است.

$$\large \begin{cases}H_0: \mu_A =\mu_B \\H_1: \mu_A < \mu_B\end{cases}$$

برای شروع کار، داده‌ها را وارد می‌کنیم.

1women_weight <- c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5)
2men_weight <- c(67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4,63.2,88,62.1)

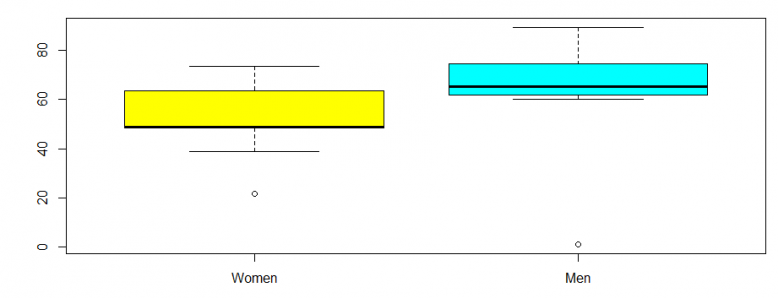
بهتر است برای بررسی برابر بودن واریانس هر دو گروه که از پیش‌فرض‌های آزمون تی دو نمونه‌ای است، از یک نمودار جعبه‌ای کمک بگیریم. کد زیر نمودار جعبه‌ای را برای وزن هر دو گروه ترسیم و مقایسه می‌کند.

1boxplot(women_weight,men_weight,col = c(31,5),names=c("Women","Men"))

پس از اجرای دستور $$()boxplot$$ نموداری مانند تصویر زیر ایجاد خواهد شد. از آنجایی که ارتفاع جعبه‌ها یکسان به نظر می‌رسد می‌توان برابری واریانس‌های دو گروه را مورد تایید قرار داد.

همچنین برای آزمون برابری واریانس‌ها نیز می‌توان از تابع $$var.test()$$‌ استفاده کرد. این آزمون از آماره F برای انجام آزمون نسبت واریانس‌ها استفاده می‌کند. کافی است کد دستوری زیرا را وارد کنیم تا برای این مثال آزمون برابری واریانس های وزن گروه دانشجویان دختر و پسر اجرا شود. شکل دستوری و خروجی آن در ادامه قابل مشاهده است.

1> var.test(women_weight,men_weight)
2
3	F test to compare two variances
4
5data:  women_weight and men_weight
6F = 2.3426, num df = 8, denom df = 11, p-value = 0.1915
7alternative hypothesis: true ratio of variances is not equal to 1
895 percent confidence interval:
9 0.6393944 9.9407261
10sample estimates:
11ratio of variances 
12          2.342625 
13
14>

فرضیه‌های چنین آزمونی به صورت زیر نوشته می‌شود.

$$\large \begin{cases}H_0: \dfrac{\sigma_A}{\sigma_B}=1 \\H_1: \dfrac{\sigma_A}{\sigma_B} \neq 1 \end{cases}$$

همانطور که دیده می‌شود، با توجه به مقدار احتمال (p-value) که برابر با 0.1915 و بزرگتر از احتمال خطای نوع اول ($$\alpha$$) است، دلیلی بر رد فرض صفر وجود ندارد. بنابراین می‌توان واریانس هر دو گروه را برابر در نظر گرفت.

حال از آزمون مقایسه میانگین تی استفاده می‌کنیم و فرض برابری واریانس‌ها را نیز در نظر می‌گیریم. بنابراین شکل دستوری تابع $$t.test()$$ در این مثال به صورت زیر خواهد بود. البته خروجی را هم در ادامه دستور می بینید.

1> t.test(women_weight,men_weight,paired = FALSE,var.equal = TRUE ,alternative = "less")
2
3	Two Sample t-test
4
5data:  women_weight and men_weight
6t = -3.098, df = 19, p-value = 0.002961
7alternative hypothesis: true difference in means is less than 0
895 percent confidence interval:
9      -Inf -7.695714
10sample estimates:
11mean of x mean of y 
12 52.10000  69.51667 

نکته: برای نشان دادن آزمون یکطرفه از پارامتر $$alternative="less"$$ استفاده کرده‌ایم.

با توجه به مقدار p-value=0.002961 فرض صفر در سطح خطای $$\alpha=0.05$$ رد می‌شود. بنابراین می‌توان وزن گروه دانشجویان دختر را کمتر از گروه دانشجویان پسر در نظر گرفت. در انتها نیز میانگین وزن دانشجویان دختر (52.1) و پسر (69.51667) ذکر شده. به این ترتیب می‌توان گفت که جنسیت عامل تاثیرگذار بر وزن دانشجویان است.

مثال ۳

در مثال قبلی به بررسی میانگین دو متغیر مستقل از یکدیگر پرداختیم. ولی گاهی ممکن است شکلی که برای ورود این داده‌ها در نظر گرفته‌ایم با مثال قبل متفاوت باشد. در این مثال از دو متغیر «وزن» (Weight) و «جنسیت» (Gender) برای نگهداری اطلاعات استفاده کرده‌ایم. فرض کنید در متغیر gender مقدارهای ۱ برای دختران و ۲ برای پسران و در جلوی هر یک از این مقدارها نیز وزن مربوط به آن فرد ثبت شده است. جدول اطلاعاتی در این حالت به صورت زیر است.

فرض کنید، این اطلاعات در یک «چارچوب اطلاعاتی» (Dataframe) به نام data ثبت شده‌اند.

1> data
2   weight gender
31    38.9      1
42    61.2      1
53    73.3      1
64    21.8      1
75    63.4      1
86    64.6      1
97    48.4      1
108    48.8      1
119    48.5      1
1210   67.8      2
1311   60.0      2
1412   63.4      2
1513   76.0      2
1614   89.4      2
1715   73.3      2
1816   67.3      2
1917   61.3      2
2018   62.4      2
2119   63.2      2
2220   88.0      2
2321   62.1      2
24> class(data)
25[1] "data.frame"

باز هم هدف انجام آزمون تی برای مقایسه میانگین بین این دو گروه است. این بار از شیوه دیگری از تابع $$t.test()$$‌ استفاده می‌کنیم.

1gender=as.factor(gender)
2class(gender)
3t.test(weight~gender,data,var.equal=TRUE, alternative="less")

پارامترها در این حالت با ذکر یک فرمول یا رابطه بین متغیر عامل (جنسیت) و متغیر وابسته (وزن) مشخص می‌کنیم که متغیر دسته‌بندی برای ایجاد گروه‌ها gender و برای محاسبه میانگین هر گروه برای متغیر weight صورت می‌گیرد. پارامترهای این شیوه استفاده از تابع $$t.test()$$ در جدول زیر معرفی شده‌اند.

1formula	
2a formula of the form lhs ~ rhs where lhs is a numeric variable giving the data values and rhs a factor with two levels giving the corresponding groups.
3data	
4an optional matrix or data frame (or similar: see model.frame) containing the variables in the formula formula. By default the variables are taken from environment(formula).

البته توجه داشته باشید که در این شیوه آزمون، فرضیات به صورت زیر نوشته شده‌اند.

$$\large \begin{cases}H_0: \mu_A -\mu_B=0 \\H_1: \mu_A -\mu_B \neq 0 \end{cases}$$

در این حالت تفاضل میانگین‌ها مورد قضاوت قرار گرفته است ولی نتیجه هر دو شیوه آزمون (براساس دو متغیر مستقل یا براساس یک متغیر عامل و یک متغیر وابسته) یکسان خواهد بود. به این ترتیب، خروجی درست به مانند قبل است. فقط باید توجه داشت که فرضیه‌های آزمون به صورتی است که در بالا به آن اشاره شد. به همین دلیل فاصله اطمینان برای تفاضل میانگین دو جامعه بدست آمده است.

1> t.test(weight~gender,data,var.equal=TRUE, alternative="less")
2
3	Two Sample t-test
4
5data:  weight by gender
6t = -3.098, df = 19, p-value = 0.002961
7alternative hypothesis: true difference in means is less than 0
895 percent confidence interval:
9      -Inf -7.695714
10sample estimates:
11mean in group 1 mean in group 2 
12       52.10000        69.51667 
13
14>

آزمون تی نمونه‌های وابسته (Paired Sample T Test)

آزمون تی دو نمونه‌ای یا آزمون تی زوجی از این جهت که برآورد واریانس در آماره آزمون آن متفاوت با حالت آزمون دو نمونه مستقل است مورد بحث قرار می‌گیرد. از این گونه آزمون بخصوص در زمانی که برای هر مشاهده دوبار اندازه‌گیری یک متغیر کمی صورت گرفته، استفاده می‌شود.

فیلم آموزش تجزیه و تحلیل داده های کشاورزی با نرم افزار MSTAT-C‎ در فرادرس

کلیک کنید

برای آشنایی بیشتر مسائل مرتبط با این آزمون به مثالی که در ادامه آمده‌، توجه کنید.

• تاثیر تبلیغ در میزان فروش، قبل از تبلیغ فروش‌ها اندازه‌گیری شده و بعد از اجرای تبلیغ نیز میزان فروش در یک دوره یک ماهه اندازه‌گیری می‌شود. اگر عوامل دیگیری در این میان نقش نداشته باشند، تغییر در میزان فروش تحت تاثیر تبلیغ بوجود آمده است.
• تاثیر داروی فشار خون در بیماران فشار خونی، قبل از تجویز دارو، فشار خون بیماران اندازه‌گیری می‌شود. پس از مصرف دارو نیز فشار خون همان بیماران اندازه‌گیری شده و تغییر در فشار خون، تاثیر دارو را نشان می‌دهد.
• از میان دو قلوها (که به نظر می‌رسد دارای بهره هوشی یکسانی هستند) یک قل را در گروه A و قل دیگر را در گروه B قرار می‌دهیم. هر گروه را تحت شیوه‌های آموزشی متفاوتی قرار می‌دهیم. مشخص است که تعداد افراد در هر دو گروه یکسان هستند. در این حالت برای نشان دادن شیوه آموزشی برتر می‌توان از آزمون تی نمونه‌های وابسته استفاده کرد.

در همه این موارد، مقدارهای یک متغیر کمی، قبل و بعد از اثر یک عامل بر روی افراد یکسان یا مشابه (دو قلوها یا با بهره هوشی یکسان) جمع‌آوری شده و تحت آزمون قرار می‌گیرد. در اینجا نیز فرضیات مربوط به آزمون به صورت زیر نوشته خواهند شد.

$$\large \begin{cases}H_0: \mu_A =\mu_B \\H_1: \mu_A \neq \mu_B\end{cases}$$

نکته: باز هم توجه داشته باشید که دراین حالت برابر بودن واریانس‌ها و توزیع نرمال باید در نظر گرفته شود.

آماره آزمون برای آزمون نمونه‌های وابسته یا زوجی تی به صورت زیر نوشته می‌شود.

$$\large T=\dfrac{\bar{d}}{\dfrac{s}{\sqrt{n}}}$$

در این رابطه منظور $$\bar{d}$$ میانگین اختلاف‌های دو متغیر (قبل و بعد از اثر) است. این آماره دارای توزیع t با n-1 درجه آزادی است. همچنین $$s$$ نیز انحراف استاندارد d را نشان می‌دهد. در این حالت داریم:

$$\large d_i=x{_{i_A}}-x{_{i_B}}, \;\;i=1,2,\cdots,n$$

در نتیجه می‌توان مقدار $$\bar{d}$$ و $$s$$ را به صورت زیر محاسبه کرد.

$$\large \bar{d}=\dfrac{1}{n}\sum_{i-1}^nd_i$$

$$\large s^2=\dfrac{1}{n-1}\sum_{i=1}^n (d_i-\bar{d})$$

مثال ۴

میزان فشار خون ۱۰ بیمار قبل و بعد از مصرف دارو ثبت شده است. می‌خواهیم تاثیر این دارو را بر میزان فشار خون بیازماییم. اطلاعات این بیماران در جدول زیر نوشته شده است.

سطر اول جدول شماره بیمار و سطر دوم فشار خون قبل از مصرف دارو سطر سوم نیز فشار خون بعد از مصرف دارو را نشان می‌دهد. آیا دارو در کاهش میزان فشار خون موثر است؟ از آنجایی که از هر بیمار دوبار اندازه‌گیری صورت گرفته، باید از آزمون زوجی تی استفاده کرد.

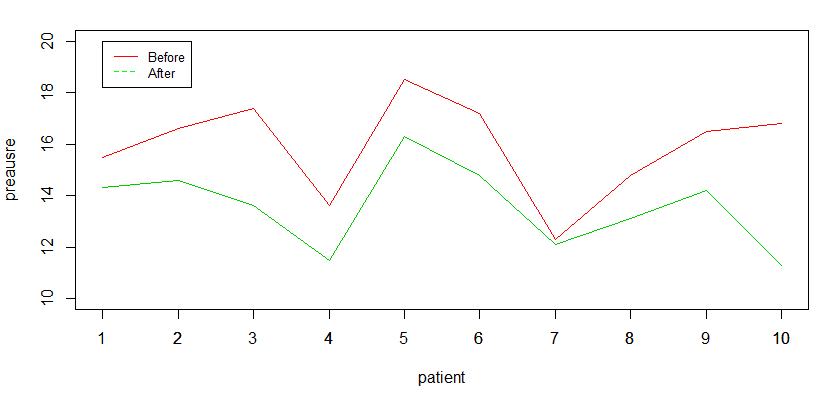
شیوه اجرای دستورات در R درست به مانند قبل است فقط کافی است که گزینه $$paired=TRUE$$ باشد. ابتدا براساس یک نمودار وضعیت بیماران را قبل و بعد از مصرف دارو بررسی کرده، سپس آزمون آماری را اجرا می‌کنیم.

1before=c(15.5,16.6,17.4,13.6,18.5,17.2,12.3,14.8,16.5,16.8)
2after=c(14.3,14.6,13.6,11.5,16.3,14.8,12.1,13.1,14.2,11.3)
3plot(before,type ="l",xlim=c(1,10),ylim = c(10,20),col=2,xlab = "patient",ylab="preausre")
4lines(after,col=3)
5legend(1, 20, legend=c("Before", "After"),
6       col=c("red", "Green"), lty=1:2, cex=0.8)
7axis(1,labels = seq(1:10),at = 1:10)

همانطور که در تصویر زیر می بینید، مشخص است که بعد از مصرف دارو، به میزان قابل توجهی، فشار خون افراد کاهش پیدا کرده است. یعنی به نظر می‌رسد باید تفاوت معنی‌داری بین فشار خون قبل از مصرف دارو (before) و بعد از آن (after) وجود داشته باشد.

حال دستورات مربوط به انجام آزمون آماری را اجرا می‌کنیم.

1var.test(before,after)
2t.test(before,after,paired = TRUE,var.equal = TRUE,alternative="greater")

ابتدا آزمون برابری واریانس‌ها اجرا شده است. در صورتی که این فرض تایید شود، آزمون مقایسه میانگین‌ها بین زوج‌ها از طریق فرض برابری واریانس‌ها انجام خواهد شد. مشخص است که پارامتر $$alternative="greater"$$ به علت آزمون یکطرفه نوشته شده است. همچنین paired نیز با TRUE مقدار دهی شده است. خروجی به شکل زیر خواهد بود.

1> var.test(before,after)
2
3	F test to compare two variances
4
5data:  before and after
6F = 1.4039, num df = 9, denom df = 9, p-value = 0.6214
7alternative hypothesis: true ratio of variances is not equal to 1
895 percent confidence interval:
9 0.3487173 5.6522299
10sample estimates:
11ratio of variances 
12          1.403934 

از آنجایی که آزمون برابری واریانس‌ها با مقدار احتمال p-values=0.6214 در سطح آزمون 0.05، مورد تایید قرار گرفته‌است، آزمون مقایسه میانگین با فرض برابری واریانس‌ها اجرا شده است. نتیجه این آزمون نیز در ادامه قابل مشاهده است.

1> t.test(before,after,paired = TRUE,var.equal = TRUE,alternative="greater")
2
3	Paired t-test
4
5data:  before and after
6t = 5.1468, df = 9, p-value = 0.0003029
7alternative hypothesis: true difference in means is greater than 0
895 percent confidence interval:
9 1.506566      Inf
10sample estimates:
11mean of the differences 
12                   2.34 
13
14>

با توجه به مقدار p-value=0.0003029 در سطح آزمون 0.05، فرض صفر رد شده و فرض برابری میانگین فشار خون، قبل و بعد از مصرف دارو، رد می‌شود. از انجایی که این آزمون یکطرفه بود، مشخص می‌شود که مصرف دارو در کاهش فشار خون موثر است.

خلاصه

آنچه در اجرای آزمون تی مهم است، نرمال بوده جامعه آماری است. آنچه به عنوان آماره آزمون و توزیع آن شناختیم با فرض نرمال بودن جامعه آماری تعیین شده بود. در نتیجه سنجش و آزمون نرمال بودن داده‌ها نیز از اهمیت زیادی برخوردار است که در مطالب دیگر فرادرس به آن‌ها اشاره خواهیم داشت.

جدول زیر به بررسی خصوصیات و پارامترهای تابع $$t.test()$$ در R به منظور آزمون میانگین پرداخته است.

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آمار و احتمال مهندسی
•  آموزش برنامه‌نویسی R و نرم‌افزار R Studio
• آموزش تکمیلی برنامه‌نویسی R و نرم‌افزار RStudio
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• آموزش آزمون آماری و پی مقدار (p-value)
• بررسی توابع خانواده apply در R

^^