نمایش سیستم های دینامیکی با متلب – از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش قبلی، مدل‌سازی سیستم‌های دینامیکی را در قالب نمایش فضای حالت و تابع تبدیل توضیح دادیم. در این آموزش، مثال‌هایی از مدل‌سازی سیستم‌های مکانیکی و الکتریکی را بررسی خواهیم کرد. همچنین، نحوه نمایش این سیستم‌ها را در نرم‌افزار متلب (MATLAB) بیان می‌کنیم.

سیستم‌های مکانیکی

پایه تحلیل سیستم‌های مکانیکی، قانون نیوتن است. قانون دوم نیوتن (رابطه (۱))، بیان می‌کند که مجموع نیروهای وارد بر یک جسم، برابر با حاصل‌ضرب جرم جسم در شتاب آن است. قانون سوم نیوتن نیز بیان می‌کند وقتی دو جسم در تماس با هم هستند، نیروهایی با بزرگی یکسان و جهت مخالف به هم وارد می‌کنند.

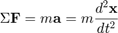
هنگام اعمال رابطه بالا، بهترین کار این است که نمودار جسم آزاد (free-body diagram) یا FBD سیستم را رسم کنیم.

مثال: سیستم جرم-فنر-دمپر

شکل زیر، سیستم جرم-فنر-دمپر را نشان می‌دهد:

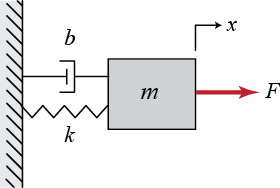
نمودار جسم آزاد سیستم در شکل زیر آورده شده است. نیروی فنر با جابجایی $$x$$ جرم رابطه مستقیم دارد و نیروی میرایی لَخت با سرعت جسم رابطه تناسبی دارد ($$v=\dot{x}$$). هر دو نیرو در جهت عکس حرکت و منفی محور $$x$$ هستند. لازم به ذکر است که $$x=0$$ متناظر با موقعیت جسم در حالتی است که فنر کشیده نشده است.

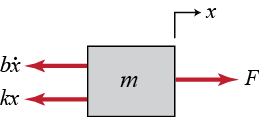
اکنون، با جمع نیروها در هر جهت و اعمال قانون دوم نیوتن (رابطه (۱))، می‌توانیم معادله دینامیکی سیستم را به دست آوریم (در این‌جا نیروها فقط در جهت محور $$x$$ هستند):

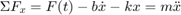
رابطه بالا، معادله حاکم (governing equation) نامیده می‌شود و دینامیک سیستم را نشان می‌دهد. با این معادله می‌توانیم پاسخ سیستم به هر ورودی $$F(t)$$ را به دست آوریم. همچنین می توانیم پایداری و عملکرد آن را بررسی کنیم.

برای محاسبه نمایش فضای حالت سیستم، باید معادله حاکم مرتبه دوم را به مجموعه معادلات دیفرانسیل مرتبه اول تبدیل کنیم. برای این منظور، موقعیت و سرعت را به عنوان متغیرهای حالت در نظر می‌گیریم.

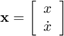
متغیر موقعیت، انرژی پتانسیل ذخیره شده در فنر را نشان می‌دهد و متغیر سرعت، نمایان‌گر انرژی جنبشی ذخیره شده در فنر است. دمپر فقط انرژی تلف می‌کند و آن را ذخیره نمی‌کند. هنگام انتخاب متغیرهای حالت، پیدا کردن متغیرهایی که انرژی ذخیره می‌کنند مفید خواهد بود.

با این اوصاف، معادله حالت به صورت زیر است:

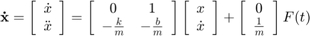
اگر بخواهیم موقعیت جسم را مشاهده کنیم، معادله خروجی به صورت زیر خواهد بود:

$$y = [ 1 \;\;\;0] \begin{bmatrix} x \\ \dot {x} \end {bmatrix}$$

رابطه (۵)

تعریف مدل فضای حالت در متلب

در این‌جا، چگونگی تعریف معادلات بالا را در m-file متلب توضیح می‌دهیم. ابتدا مقادیر عددی متغیرهای زیر را در نظر می‌گیریم:

  %m                mass                                     1.0 kg
  %k                spring constant                          1.0 N/m  
  %b                damping constant                         0.2 Ns/m   
  %F                input force                              1.0 N

یک m-file جدید ایجاد کرده و مقادیر زیر را در آن وارد می‌کنیم:

پاسخ به صورت زیر خواهد بود:

تبدیلا لاپلاس سیستم، با فرض شرایط اولیه صفر برابر با رابطه زیر است:

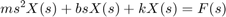
و تابع تبدیل ورودی نیرو به خروجی جابجایی به صورت زیر خواهد بود:

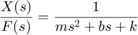
اکنون می‌خواهیم تابع تبدیل را در متلب تعریف کنیم. بدین منظور، دستورهای زیر را در m-file متلب می‌نویسیم:

که پاسخ آن به صورت زیر است:

در کد بالا، از متغیر نمادین s برای تعریف مدل تابع تبدیل استفاده کردیم. اغلب همین کار برای تعریف تابع تبدیل پیشنهاد می‌شود، اما در برخی شرایط به خاطر نسخه‌های متلب یا مواقعی که با سیمولینک (SIMULINK) کار می‌کنیم، ممکن است بخواهیم تابع تبدیل را با ضرایب چندجمله‌ای صورت و مخرج تعریف کنیم. در این موارد، از دستورهای زیر استفاده می‌کنیم:

که پاسخ آن به صورت زیر خواهد بود:

سیستم‌های الکتریکی

مشابه قوانین نیوتن برای سیستم‌های مکانیکی، قوانین مداری کیرشهف ابزار اساسی مدل‌سازی مدارهای الکتریکی هستند. قانون جریان کیرشهف (KCL) بیان می‌کند که مجموع جریان‌های وارد شده به یک گره، برابر با مجموع جریان‌های خارج شده از آن است. قانون ولتاژ کیرشهف (KVL) بیان می‌کند مجموع اختلاف ولتاژهای هر حلقه بسته در مدار صفر است. وقتی از KVL استفاده می‌کنیم، اختلاف ولتاژ منابع ولتاژ مثبت و اختلاف ولتاژ بارها را منفی در نظر می‌گیریم.

فیلم آموزش فیزیک ۲ دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

مثال: مدار RLC

اکنون یک مدار RLC‌ ساده را در نظر می‌گیریم که در آن، سه عنصر پسیو مقاومت، سلف و خازن با هم سری شده‌اند.

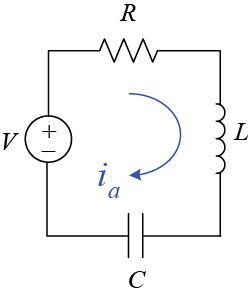
با اعمال KVL در حلقه، به معادله حاکم زیر می‌رسیم:

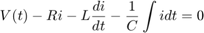
این رابطه به نوعی شبیه سیستم جر- فنر-دمپر است. به طور خاص، این دو سیستم، مرتبه دوم هستند که بار الکتریکی (انتگرال جریان)، اندوکتانس سلف، مقاومت و به ترتیب متناظر با جابجایی، جرم و میرایی لخت هستند.

با انتخاب بار خازن و جریان سلف به عنوان متغیرهای حالت، می‌توان نوشت:

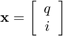
که در آن،

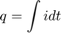
در نتیجه، معادله حالت به صورت زیر خواهد بود:

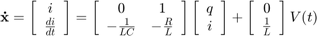
جریان را به عنوان خروجی در نظر می‌گیریم. پس داریم:

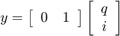
تابع تبدیل سیستم را می‌توان با استفاده از تبدیل لاپلاس یا رابطه زیر پیدا کرد:

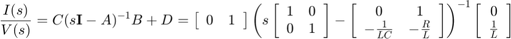
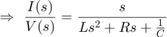
مدل فضای حالت و تابع تبدیل مدار RLC‌ را می‌توان به صورت مشابه در متلب تعریف کرد.

^^