تانسور نرخ کرنش (Strain Rate Tensor) – آشنایی با خصوصیات رفتاری مواد

«تانسور نرخ کرنش» (Strain Rate Tensor)، یک کمیت فیزیکی در مکانیک محیط‌های پیوسته است که تغییر شکل ماده در مجاورت یک نقطه مشخص را در یک لحظه خاص توصیف می‌کند. با مشتق گرفتن از تانسور کرنش نسبت به زمان یا مشتق گرفتن از جریان سرعت نسبت به مکان (مؤلفه‌های متقارن گرادیان جریان سرعت) می‌توان تانسور نرخ کرنش را به دست آورد. تانسور نرخ کرنش، صرفاً یک مفهوم جنبشی است که امکان توصیف حرکت مواد در مقیاس ماکروسکوپی را فراهم می‌کند. از این‌رو، این مفهوم به ماهیت ماده یا تنش‌ها و نیروهای احتمالی بستگی ندارد و در تمام محیط‌های پیوسته (جامد، مایع یا گاز) قابل محاسبه است.

از طرف دیگر، برای تمام مواد سیال (به استثنای ابر سیالات)، به دلیل وجود اصطکاک بین المان‌های مجاور مواد، هرگونه تغییر شکل تدریجی (تانسور نرخ کرنش غیر صفر) باعث افزایش نیروهای ویسکوز در داخل سیال می‌شود. این نیروها، در برابر تغییرات مقاومت می‌کنند و تمایل به برگرداندن ماده به حالت اول دارند. تنش‌های موجود در هر نقطه درون یک سیال را می‌توان با استفاده از «تانسور تنش ویسکوز» (Viscous Stress Tensor) توصیف کرد. به علاوه، تقریباً در همه موارد امکان تعیین این تانسور توسط تانسور نرخ کرنش و برخی از خصوصیات ذاتی سیال در نقطه مورد نظر وجود دارد. در جامدات، علاوه بر تنش الاستیک موجود در تغییر شکل‌های استاتیک، تنش ویسکوز نیز رخ می‌دهد. هنگامی که مقدار این تنش‌ها به اندازه کافی بزرگ باشد، ماده دارای خاصیت «ویسکوالاستیسیته» (Viscoelasticity) خواهد بود. مواد ویسکوالاستیک، رفتاری میان دو خاصیت کلی ویسکوز بودن و کشسان بودن را از خود به نمایش می‌گذارند.

تعریف ریاضی تانسور نرخ کرنش

یک جسم جامد در حال حرکت یا مایع در حال جریان را در نظر بگیرید. فرض کنید v، میدان سرعت درون جسم و یک تابع هموار از R³*R باشد. به این ترتیب، (v(p,t، سرعت ماکروسکوپی گذرنده از نقطه p در زمان t را نشان می‌دهد.

سرعت (v(p+r,t در نقطه‌ای با فاصله برداری r از p را می‌توان به صورت یک سری تیلور نوشت:

$${\displaystyle \mathbf {v} (\mathbf {p} +\mathbf {r},t)=\mathbf {v} (\mathbf {p},t)+(\nabla \mathbf {v})(\mathbf {p},t)(\mathbf {r})+{\text{Higher order terms}}}$$

در معادله بالا، گرادیان میدان سرعت (v∇)، به عنوان یک نگاشت خطی در نظر گرفته می‌شود که بردار جابجایی r را به تغییرات متناظر سرعت مرتبط می‌کند.

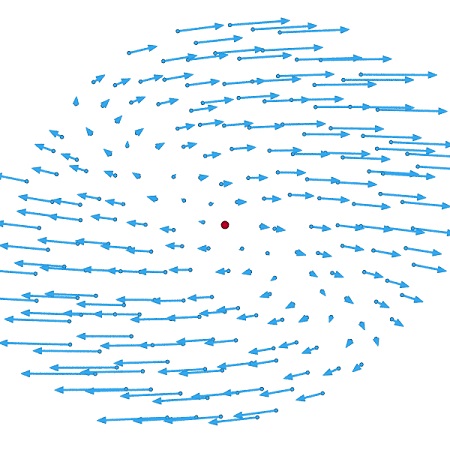
شکل‌های بالا میدان سرعت (v(p+r,t برای هر جریان دلخواه اطراف نقطه p (نقطه قرمز) در لحظه t و عبارات مرتبه اول تخمین تیلور در نزدیکی p را نشان می‌دهد. مؤلفه سوم سرعت (در امتداد داخل صفحه) در همه جا صفر در نظر گرفته می‌شود. در یک چارچوب مرجع دلخواه، v∇ به ماتریس جاکوبی میدان مرتبط است. به عنوان مثال، در فضای سه‌بعدی ماتریس 3*3 زیر را خواهیم داشت:

$${\displaystyle (\nabla \mathbf {v})={\begin{bmatrix}\displaystyle {\partial _{1}v_{1}}&\displaystyle {\partial _{2}v_{1}}&\displaystyle {\partial _{3}v_{1}}\\ \displaystyle {\partial _{1}v_{2}}&\displaystyle {\partial _{2}v_{2}}&\displaystyle {\partial _{3}v_{2}}\\ \displaystyle {\partial _{1}v_{3}}&\displaystyle {\partial _{2}v_{3}}&\displaystyle {\partial _{3}v_{3}}\end{bmatrix}}=\mathbf {J} }$$

v_i: مؤلفه v که با محور i موازی است؛ _jf∂: مشتق جزئی تابع f نسبت به مختصات فضایی x_j را نشان می‌دهد؛ J: تابعی از p و t است.

در این دستگاه مختصات، تخمین تیلور برای محاسبه سرعت در نزدیکی نقطه p به صورت زیر خواهد بود:

$${\displaystyle v_{i}(\mathbf {p} +\mathbf {r},t)=v_{i}(\mathbf {p},t)+\sum _{j}J_{ij}(\mathbf {p},t)r_{j}=v_{i}(\mathbf {p},t)+\sum _{j}\partial _{j}v_{i}(\mathbf {p},t)r_{j}}$$

اگر v و t ماتریس‌های 3*1 باشند، معادله بالا را می‌توان به صورت زیر نمایش داد:

$${\displaystyle \mathbf {v} (\mathbf {p} +\mathbf {r},t)=\mathbf {v} (\mathbf {p},t)+\mathbf {J} (\mathbf {p},t)\mathbf {r}}$$

برای درک بهتر مفاهیم پیشرفته تنش، ابتدا باید با مفاهیم اولیه مقاومت مصالح و خصوصیات رفتاری مواد آشنا باشید. به این منظور، مطالعه مطلب «مقاومت مصالح چیست؟ – پارامترها و مفاهیم پایه به زبان ساده» را به شما پیشنهاد می‌کنیم.

بخش‌های متقارن و نامتقارن تانسور کرنش

تمام ماتریس‌ها را می‌توان به صورت حاصل جمع یک ماتریس متقارن با یک ماتریس پادمتقارن تجزیه کرد.

فیلم آموزش خواص مکانیکی مواد ۲ در فرادرس

کلیک کنید

اگر بخواهیم این عملیات را روی ماتریس جاکوبی J = (∇v)T با مؤلفه‌های متقارنِ E و پادمتقارنِ R اعمال کنیم، خواهیم داشت:

$${\displaystyle \mathbf {E} ={\tfrac {1}{2}}\left(\mathbf {J} +\mathbf {J} ^{\mathrm {T} }\right)\qquad \mathbf {R} ={\tfrac {1}{2}}\left(\mathbf {J} -\mathbf {J} ^{\mathrm {T} }\right)}$$

معادلات بالا را می‌توان به صورت زیر نوشت:

$${\displaystyle E_{ij}={\tfrac {1}{2}}(\partial _{j}v_{i}+\partial _{i}v_{j})\qquad R_{ij}={\tfrac {1}{2}}(\partial _{j}v_{i}-\partial _{i}v_{j})}$$

این تجزیه، مستقل از دستگاه مختصات بوده و به همین دلیل، دارای مفهوم فیزیکی است. از این‌رو، برای تخمین میدان سرعت خواهیم داشت:

$${\displaystyle \mathbf {v} (\mathbf {p} +\mathbf {r},t)\approx \mathbf {v} (\mathbf {p},t)+\mathbf {E} (\mathbf {p},t)(\mathbf {r})+\mathbf {R} (\mathbf {p},t)(\mathbf {r})}$$

که در آن:

$${\displaystyle {\begin{aligned}v_{i}(\mathbf {p} +\mathbf {r},t)&=v_{i}(\mathbf {p},t)+\sum _{j}E_{ij}(\mathbf {p},t)r_{j}+\sum _{j}R_{ij}(\mathbf {p},t)r_{j}\\&=v_{i}(\mathbf {p},t)+{\tfrac {1}{2}}\sum _{j}{\big (}\partial _{j}v_{i}(\mathbf {p},t)+\partial _{i}v_{j}(\mathbf {p},t){\big)}r_{j}+{\tfrac {1}{2}}\sum _{j}{\big (}\partial _{j}v_{i}(\mathbf {p},t)-\partial _{i}v_{j}(\mathbf {p},t){\big)}r_{j}\end{aligned}}}$$

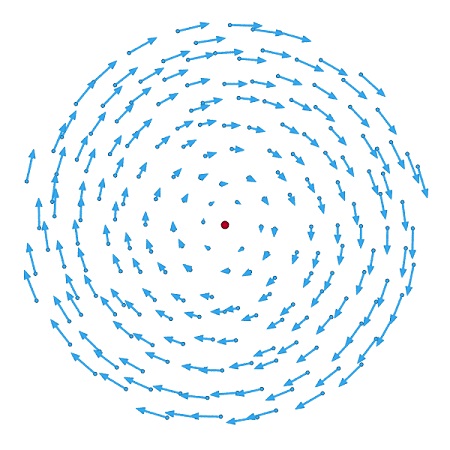
عبارت پادمتقارنِ R، بیانگر چرخش صلب گونه سیال در اطراف نقطه p است. سرعت زاویه‌ای این سیال توسط رابطه زیر به دست می‌آید:

$${\displaystyle \omega ={\tfrac {1}{2}}\nabla \times \mathbf {v} ={\tfrac {1}{2}}{\begin{bmatrix}\partial _{2}v_{3}-\partial _{3}v_{2}\\\partial _{3}v_{1}-\partial _{1}v_{3}\\\partial _{1}v_{2}-\partial _{2}v_{1}\end{bmatrix}}}$$

حاصل عبارت v×∇، با عنوان «تابِ دورانی» (Rotational Curl) میدان سرعت شناخته می‌شود. در یک چرخش صلب، موقعیت‌های نسبی المان‌های سیال تغییر نمی‌کنند. از این‌رو، عبارت پادمتقارن R در گرادیان سرعت، تأثیری بر روی نرخ تغییر شکل ندارد. بنابراین، نرخ کرنش واقعی توسط عبارت متقارن E توصیف می‌شود. این عبارت همان تانسور نرخ کرنش است.

نرخ برش و نرخ فشار

عبارت متقارن R در گرادیان سرعت (تانسور نرخ کرنش) را می‌توان به صورت حاصل جمع یک مقدار اسکالر در تانسور واحد (تراکم یا انبساط همسانگرد تدریجی) و یک تانسور متقارنِ بدون اثر (تغییر شکل برشی تدریجی با حجم ثابت) نمایش داد:

$${\displaystyle \mathbf {E} (\mathbf {p},t)(\mathbf {r})=\mathbf {D} (\mathbf {p},t)(\mathbf {r})+\mathbf {S} (\mathbf {p},t)(\mathbf {r})}$$

که در آن:

$${\displaystyle E_{ij}= {{\tfrac {1}{3}}\left(\sum _{k}\partial _{k}v_{k}\right)\delta _{ij}} +{{\tfrac {1}{2}}\left(\partial _{i}v_{j}+\partial _{j}v_{i}\right)-{\tfrac {1}{3}}\left(\sum _{k}\partial _{k}v_{k}\right)\delta _{ij}}}$$

عبارت اول، تانسور نرخ انبساط (D_ij) و عبارت دوم، تانسور نرخ برش (S_ij) را نشان می‌دهد. به علاوه، δ، تانسور واحدی است که اگر در آن i=j باشد، δ_ij برابر با 1 و اگر i≠j باشد، δ_ij برابر با 0 خواهد بود.

تجزیه بالا، مستقل از نوع دستگاه مختصات انتخاب شده است و به همین دلیل یک مفهوم فیزیکی به حساب می‌آید.

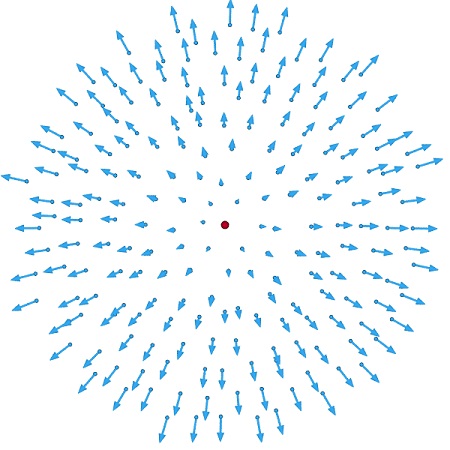
تانسور نرخ انبساط، یک سومِ دیورژانس میدان سرعت است:

$${\displaystyle \nabla \cdot \mathbf {v} =\partial _{1}v_{1}+\partial _{2}v_{2}+\partial _{3}v_{3}}$$

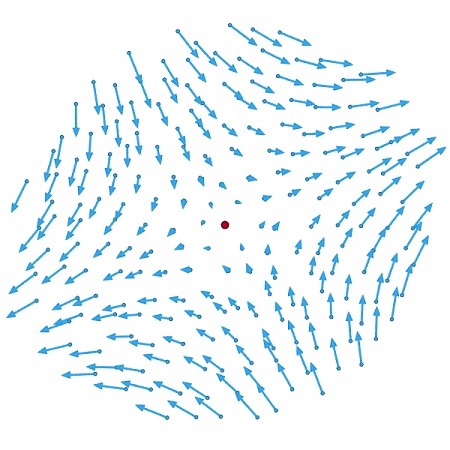
تانسور نرخ برش توسط یک ماتریس متقارن 3*3 نمایش داده می‌شود. این تانسور، معرف جریانی است که جریان‌های انبساطی و انقباضی را در امتداد سه محور متعامد و بدون تغییر حجم با هم ترکیب می‌کند. این نوع جریان در مواردی مانند ریختن عسل از روی یک قاشق به صورت یک جریان ملایم پیوسته یا کشیدن یک نوار لاستیکی از دو انتهای آن رخ می‌دهد.

برای یک جریان دوبعدی، دیورژانس v تنها دارای دو عبارت است و به جای تغییرات حجم، تغییرات مساحت را به صورت کمی درمی‌آورد. در این حالت، به منظور تعیین تانسور نرخ انبساط، یک دوم دیورژانس میدان سرعت محاسبه می‌شود.