ماتریس مشابهت (Similarity) و فاصله (Distance) به همراه کدهای محاسباتی در R — راهنمای گام به گام

به منظور دسته‌بندی و طبقه‌بندی اشیاء باید ملاکی برای اندازه‌گیری میزان مشابهت یا فاصله بین آن‌ها در نظر گرفته شود. به این ترتیب اشیائی که به یکدیگر شبیه‌تر هستند می‌توانند در یک طبقه یا گروه قرار گیرند. برای نمایش مشابهت چند شیء از «ماتریس مشابهت» (Similarity Matrix) استفاده می‌شود. در مبحث داده‌کاوی، گاهی به ماتریس مشابهت، «ماتریس مجاورت» (Proximity Matrix) نیز می‌گویند. معمولا برای اندازه‌گیری عدم مشابهت بین دو سری داده، فاصله آن‌ها را محاسبه می‌کنند. البته با استفاده از تبدیلاتی، می‌توان ماتریس فاصله را به مشابهت تبدیل کرد. از این ماتریس‌ها به منظور خوشه‌بندی و دسته‌بندی نقاط و اشیاء، در مبحث «آموزش ماشین» (Machine Learning) بخصوص «یادگیری بدون نظارت» (Unsupervised Learning) استفاده‌های زیادی می‌شود.

در این نوشتار، ابتدا به مفهوم مشابهت و فاصله پرداخته و ماتریس‌های مشابهت و فاصله را معرفی می‌کنیم. در ادامه نیز با استفاده از کدهای R و توابع مختلفی که در این زبان وجود دارد، ماتریس‌های مشابهت و فاصله را محاسبه می‌کنیم. از این گونه محاسبات در روش‌های خوشه‌بندی سلسله‌مراتبی (Hierarchical Clustering) و تفکیکی (Partition Clustering) سود خواهیم برد.

بنابراین بهتر است قبل از مطالعه این نوشتار، مطلب فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی را مطالعه کنید . همچنین به منظور آشنایی با ماتریس‌ها و عملیات قابل انجام روی آن‌ها، مطالعه مطلب ماتریس‌ها — به زبان ساده مفید خواهد بود.

ماتریس مشابهت و فاصله

می‌دانیم که ماتریس، نمایشی منظم از اعداد و ارقام است که از تعدادی سطر و ستون تشکیل شده. به این ترتیب ساختاری برای نمایش بهتر رابطه بین مجموعه‌ای از نقطه‌ها فراهم می‌شود. اگر تعداد سطرها و ستون‌های یک ماتریس برابر باشد، آن را یک ماتریس مربعی می‌گویند.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

در این حالت، قطر اصلی ماتریس، مجموعه مقدارهایی است که دارای شماره سطر و ستون یکسانی هستند. اگر مقدارهای درون یک ماتریس فقط بر روی قطر اصلی قرار داشته باشند، ماتریس را «قطری» (Diagonal) می‌نامند.

ماتریسی که مقدارهای متناظر در بالا و پایین قطر اصلی آن با هم برابر باشد، یک ماتریس «متقارن» (Symmetric) نامیده می‌شود. همچنین اگر مقدارهای بالای قطر اصلی همگی صفر باشند، ماتریس را پایین مثلثی و به همین ترتیب اگر مقدارهای پایین قطر اصلی صفر باشند، ماتریس را بالا مثلثی می‌گویند.

اگر مقدارهای درون ماتریس، فاصله بین نقاط سطرها و ستون‌ها را نشان دهند، یک ماتریس فاصله شکل گرفته است. به همین ترتیب می‌توان یک ماتریس مشابهت را تعریف کرد.

همانطور که دیده می‌شود، ماتریس مشابهت و فاصله باید به شکلی باشند که بتوانند برای هر دو مقدار، تابع مشابهت و یا فاصله را نشان دهند. بنابراین ابتدا به معرفی تابع مشابهت و فاصله می‌پردازیم.

تابع مشابهت (Similarity Function)

فرض کنید «مجموعه داده» (DataSet) از نقاط یک بعدی به مانند D دارید. اگر تابع S در شرایط زیر صدق کند، آن را یک تابع مشابهت می‌نامیم.

1. $$\large s(x,y)\geq 0,\;\;\;x , y \in D$$
2. $$\large s(x,x)=1$$
3. $$\large \forall x,y \in D, \;\;s(x,y)=s(y,x)$$

با توجه به این خصوصیات مشخص است که تابع مشابهت نامنفی و برد آن فاصله بین ۰ تا ۱ است. همچنین رابطه شماره ۳ نشان می‌دهد که این تابع متقارن نیز هست. برای مثال اگر x و y‌ مقدارهای ۰ و ۱ (باینری) را بگیرند، میزان مشابهت بین این دو را می‌توان با تابع زیر اندازه‌گیری کرد.

$$\large f(x,y)=1-|x-y|$$       تابع مشابهت باینری 

همانطور که دیده می‌شود، مقدار این تابع نامنفی است و متقارن نیز هست. همچنین مشابهت هر نقطه با خودش نیز برابر با ۱ است. در نتیجه از این تابع مشابهت برای داده‌های باینری می‌توان استفاده کرد.

نکته: اگر خاصیت شماره ۳ برای تابعی که به منظور اندازه‌گیری میزان مشابهت به کار رفته، وجود نداشته باشد، آن را «تابع نیمه مشابهت» (Semi Similarity Function) می‌گویند.

تابع فاصله (Distance Function)

اگر تابع d یک تابع با مقدارهای حقیقی و نامنفی باشد، در صورتی که خاصیت‌های زیر برایش صدق کند، می‌تواند به عنوان یک تابع فاصله به کار رود.

1. $$\large d(x,y)\geq 0$$
2. $$\large d(x,y)=0 \longleftrightarrow x=y$$
3. $$\large d(x,y)=d(y,x)$$
4. $$\large \forall x,y,z \in D, d(x,z)\leq d(x,y)+d(y,z)$$

برای مثال فاصله اقلیدسی و منهتن از نمونه توابع فاصله محسوب می‌شوند که در این خصوصیات، صادق هستند.

ماتریس مشابهت (Similarity Matrix)

فرض کنید مجموعه D از نقاط $$x_1,x_2,\ldots,x_n$$ تشکیل شده است. براساس تابع مشابهت S، می‌توان برای هر زوج از اعضای D، مشابهت را اندازه‌گیری کرد و در ساختاری به شکل ماتریس قرار داد. بنابراین اگر $$s(x_i,x_j)=s_{ij}$$ به معنی مشابهت بین دو نقطه $$x_i$$ و $$x_j$$ باشد، این ماتریس به صورت زیر در خواهد آمد.

$$\large \begin{bmatrix}s_{11} & s_{12}&\cdots& s_{1n} \\ s_{21} & s_{22}&\cdots& s_{2n}\\ \vdots&\ddots&&\\ s_{n1} & s_{n2}&\cdots& s_{nn}\\ \end{bmatrix}$$

مشخص است که این ماتریس مشابهت، یک ماتریس مربعی است. اگر تابع S خاصیت‌های تابع مشابهت را داشته باشد می‌توان آن را به فرم ساده‌تر زیر نمایش داد.

$$\large \begin{bmatrix}1 & s_{12}&\cdots& s_{1n} \\ s_{12} & 1&\cdots& s_{2n}\\ \vdots&\ddots&&\\ s_{1n} & s_{2n}&\cdots& 1\\ \end{bmatrix}$$

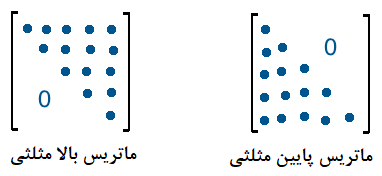
از آنجایی که تابع مشابهت متقارن است، در نتیجه ماتریس مشابهت را می‌توان به صورت یک ماتریس بالا با پایین مثلثی نمایش داد.

نکته: ماتریس مشابهت یک ماتریس بالا مثلثی یا پایین مثلثی نیست. بلکه برای نمایش آن از این حالت استفاده می‌کنیم تا در فضای نمایش ماتریس صرفه‌جویی شود. مشخص است که تقارن ماتریس مشابهت، می‌تواند توجیهی برای نمایش این ماتریس به صورت بالا یا پایین مثلثی باشد تا از تکرار مقدارهای برابر که در بالا و پایین قطر اصلی هستند، جلوگیری شود.

$$\large \begin{bmatrix}1 & s_{12}&\cdots& s_{1n} \\ & 1&\cdots& s_{2n}\\ &&\ddots&\vdots\\ & && 1\\ \end{bmatrix}$$

مثال ۱

براساس مجموعه نقاط $$D=\{0,1,1,0,1,0,1,1,0,0\}$$ و تابع مشابهت باینری که در بخش قبل معرفی شد، ماتریس مشابهت به صورت زیر در خواهد آمد.

همانطور که انتظار داریم، ماتریس مشابهت، مربعی و متقارن است. کد مربوط به محاسبه این ماتریس در ادامه قابل مشاهده است.

1D=c(0,1,1,0,1,0,1,1,0,0)
2x=D
3l= length(x)
4s= matrix(rep(0,l*l),nrow=l)
5for (i in 1:l )
6  {
7  for (j in 1 : l)
8  {
9    s[i,j]=1-abs(x[i]-x[j])
10  }
11  
12}
13s

ماتریس فاصله (Distance Matrix)

با توجه به مطلبی که در مورد ماتریس مشابهت گفته شد، می‌توان ماتریس فاصله را نیز برای نقاط محاسبه کرد. کافی است که برای هر زوج از نقطه‌ها، تابع فاصله مورد نظر را بدست آورد و در یک ماتریس قرار داد. برای آشنایی بیشتر با نحوه محاسبه ماتریس فاصله، از زبان برنامه‌نویسی R کمک می‌گیریم. در بسته‌های مختلفی که در R قرار دارد، شیوه‌های مختلفی برای محاسبه ماتریس فاصله موجود است ولی در اینجا به ساده‌ترین و مهمترین تابعی که در کتابخانه اصلی (stats) زبان برنامه نویسی R پیاده‌سازی شده، یعنی تابع dist، می‌پردازیم.

فیلم آموزش تقلیل ابعاد در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

مثال ۲

به منظور محاسبه ماتریس فاصله برای داده‌های مربوط به مثال، می‌توان از دستور dist در زبان برنامه‌نویسی R استفاده کرد. کافی است به عنوان پارامتر،‌ برداری حاوی مقدارهای مربوط به نقاط را به آن معرفی کنید. تصویر زیر ماتریس مربوط به فاصله اقلیدسی برای مثال قبل که با دستور $$dist(x)$$ تولید شده را نشان می‌دهد.

برای صرفه‌جویی در صفحه نمایش، خروجی این دستور به صورت خلاصه ظاهر شده است. به این ترتیب قطر اصلی و عناصر بالای قطر نمایش داده نشده‌اند زیرا توسط عناصر دیگر ماتریس، این مقدارها قابل محاسبه‌اند.

نکته: اگر می‌خواهید عناصر ماتریس فاصله را کامل ببینید، کافی است، دستور $$dist(x,upper = TRUE,diag = TRUE)$$ را اجرا کنید. پارامترهای دستور dist در ادامه معرفی شده‌اند.

• x: ماتریس یا مجموعه داده‌ای که باید فاصله براساس آن اندازه‌گیری شود.
• method: روش محاسبه فاصله. روش‌های مختلفی برای محاسبه فاصله در این تابع وجود دارد که با توجه به کمی یا کیفی بودن داده‌ها، قابل استفاده هستند.
• diag: مقداری منطقی (True, False) به منظور نمایش یا عدم نمایش قطر اصلی ماتریس فاصله
• upper: مقداری منطقی (True , False) به منظور نمایش یا عدم نمایش عناصر بالای قطر اصلی
• p: پارامتر تابع فاصله مینکوفسکی

اگر $$x=(x_1,x_2,\ldots,x_m)$$ و $$y=(y_1,y_2,\ldots,y_m)$$ دو نقطه m بعدی باشند، انواع فاصله‌هایی که توسط تابع dist در R برایشان قابل محاسبه است در جدول زیر آورده شده.

نکته: در این جدول در سطر پنجم منظور از Jaccard، محاسبه میزان مشابهت ژاکارد است که براساس تعداد مولفه‌های برابر در بین دو نقطه x و y محاسبه می‌شود. میزان مشابهت ژاکارد درصد مطابقت بین دو رشته باینری را اندازه‌گیری می‌کند. اگر ترتیب قرارگیری ۰ و ۱ها در هر دو رشته یکسان باشد، مقدار مشابهت ژاکارد برابر با ۱ است و اگر دو رشته هیچ دنباله یکسانی نداشته باشند، میزان مشابهت برابر با صفر خواهد بود. به همین علت برای محاسبه فاصله باینری از تفاضل ۱ از مشابهت ژاکارد استفاده شده است.

محاسبه ماتریس فاصله برای داده‌های چند بعدی

شیوه محاسبه ماتریس مشابهت یا فاصله برای داده‌های چند بعدی،‌ تفاوتی با حالت قبل ندارد فقط کافی است که نقاط را به وسیله یک ماتریس برای دستور dist معرفی کنید. برای مثال فرض کنید که می‌خواهیم ماتریس فاصله بلوکی (منهتن) بین نقطه‌هایی به مختصات $$(1,4), (3,5), (5,7)$$ را بدست آوریم. کدهای زیر به منظور محاسبه این ماتریس در زبان R نوشته شده‌اند.

1x=c(1,3,5)
2y=c(4,5,7)
3xy=cbind(x,y)
4dist(xy,method='manhattan',upper=TRUE,diag=TRUE)

خروجی این دستور مانند تصویر زیر خواهد بود. مشخص است که عناصر روی قطر اصلی برای ماتریس فاصله باید برابر با صفر باشند.

نکته: در حالت چند بعدی، ممکن است مقدارهای بزرگ در هر بعد مقدار فاصله را تحت تاثیر خود قرار دهند. برای پرهیز از این امر، بهتر است قبل از محاسبه فاصله و یا حتی مشابهت، داده‌ها را ابتدا استاندارد (بدون واحد) کنید و سپس محاسبات مربوط به فاصله یا مشابهت را براساس داده‌های استاندارد شده انجام دهید.

تبدیل ماتریس فاصله به ماتریس مشابهت

با توجه به ارتباطی که بین تابع فاصله و مشابهت وجود دارد، تبدیلاتی برای محاسبه یکی برحسب دیگری موجود است. برای مثال همانطور که دیده شد براساس رابطه $$d_{bin}=1-Jaccard(x,y)$$ می‌توان مشابهت ژاکارد را به فاصله باینری (فاصله ژاکارد) تبدیل کرد. جدول زیر به بعضی از این تبدیلات اشاره می‌کند. البته توجه داشته باشید که در اینجا s تابع مشابهت و d تابع فاصله است. همچنین ذکر این نکته ضروری است که s به عنوان تابع مشابهت دارای مقدارهایی در فاصله ۰ تا ۱ است.

نکته: اگر می‌خواهید از تبدیل‌های دیگری استفاده کنید، باید حتما شرط‌های مربوط به تابع فاصله را برای تابع و تبدیلی که ایجاده کرده‌اید، بررسی کنید.

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند.

• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
• آموزش خوشه بندی تفکیکی با نرم افزار R
• آموزش خوشه بندی سلسله مراتبی با SPSS
• فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی
• روش‌های استاندارد سازی داده‌ها
• ماتریس‌ها — به زبان ساده

^^