فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی

توابع زیادی برای اندازه‌گیری فاصله بین اشیاء، با ویژگی‌های کمی وجود دارد. «توابع فاصله» (Distance Functions) در تکنیک‌های داده‌کاوی بخصوص در خوشه‌بندی،‌ کاربردهای زیادی دارند. در این متن ابتدا به معرفی خصوصیات تابع فاصله می‌پردازیم و سپس شیوه محاسبه فاصله را براساس چند روش از جمله «فاصله اقلیدسی» (Euclidean Distance)، «فاصله منهتن» (Manhattan Distance) و «فاصله مینکوفسکی» (Minkowski Distance) بررسی می‌کنیم. این توابع فاصله بیشتر برای اندازه‌گیری میزان عدم شباهت در مباحث داده‌کاوی به کار می‌روند.

تابع فاصله

هر تابعی $$D: X\times X \to [0,\infty)$$ یک تابع فاصله است، اگر به ازاء هر سه نقطه دلخواه x, y, z در شرایط زیر صدق کند:

1. $$D(x,y)\geq 0 $$: این رابطه بیانگر نامنفی بودن تابع فاصله است.
2. $$D(x,y)=0 \longleftrightarrow x=y$$: به بیان دیگر اگر فاصله بین دو نقطه صفر باشد، دو نقطه یکی هستند و برعکس.
3. $$D(x,y)=D(y,x)$$: این رابطه، بیانگر خاصیت تقارنی برای تابع فاصله است.
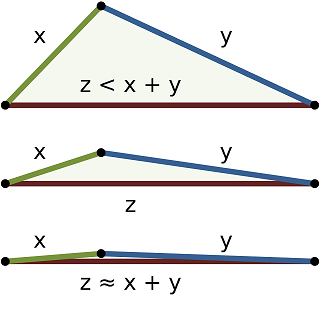
4. $$D(x,z)\leq D(x,y)+D(y,z)$$: به این معنی که تابع فاصله در نامساوی مثلثی صدق می‌کند. یعنی فاصله دو نقطه x و z کمتر از مجموع فاصله x تا y و فاصله y تا z است. این موضوع به خوبی در فاصله اقلیدسی دیده می‌شود.

فیلم آموزش مقدماتی نظریه اعداد در فرادرس

کلیک کنید

توابعی با خصوصیات گفته شده را گاهی «متریک» (Metric) نیز می‌نامند.

اگر رابطه ۴ که بیانگر رابطه مثلثی است با رابطه زیر جایگزین شود،‌ تابع فاصله را «اولترا-متریک» یا «ورا-متریک» (Ultra-metric)‌ می‌گویند.

$$D(x,z)\leq max(D(x,y),D(y,z))$$

توابعی که خاصیت اولترا-متر داشته باشند حتما متر نیز هستند. ولی عکس این موضوع صحیح نیست. زیرا مشخص است که اگر مقداری از حداکثر دو مقدار کوچکتر باشد، حتما از مجموع آن‌ها نیز کوچکتر است ولی اگر مقداری از مجموع دو عدد کوچکتر باشد دلیلی ندارد که از هر دو آن‌ها نیز کوچکتر باشد. چنانچه تابع D خاصیت شماره ۴ را نداشته باشد اصطلاحا به آن «شبه متر» (Semi-metric) گفته می‌شود. برای مثال سه عدد ۴، ۵ و ۳ را در نظر بگیرید. مشخص است که ۵ از مجموع ۴ و۳ کوچکتر است ولی ۵ از ۳ یا ۴ کوچکتر نیست.

تابع فاصله اقلیدسی

با استفاده از «فاصله اقلیدسی» (Euclidean Distance) کوتاه‌ترین فاصله بین دو نقطه برطبق رابطه فیثاغورث،‌ محاسبه می‌شود. اگر x‌ و y دو نقطه با p مولفه باشند، فاصله اقلیدسی بین این دو به صورت زیر قابل محاسبه است:

$$D_{euc}=(\sum_{i=1}^p(x_i-y_i)^2)^\tfrac{1}{2}$$

در تصویر ۱، فاصله اقلیدسی بین دو نقطه با مختصات $$(x_1,y_1)$$ با $$(x_2,y_2)$$ نشان داده شده است.

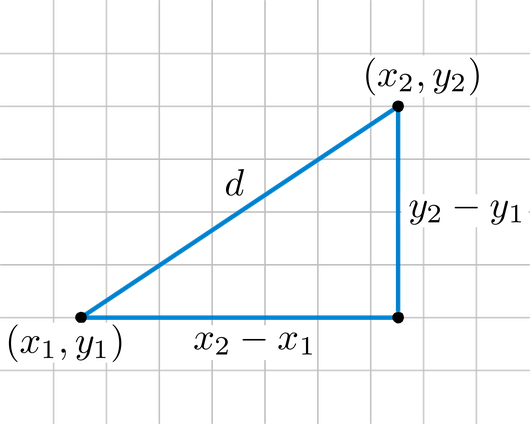
در ادامه به بررسی خصوصیات تابع فاصله برای فاصله اقلیدسی می‌پردازیم.

1. فاصله اقلیدسی باید نامنفی باشد: مشخص است که این رابطه مقداری نامنفی دارد زیرا از مجموع مربعات تفاضل‌ها ساخته شده است.
2. وجود رابطه انعکاسی برای فاصله اقلیدسی: برای نقطه‌های x و y با مقدار مولفه‌های یکسان، فاصله اقلیدسی برابر با صفر خواهد بود. همچنین زمانی که فاصله اقلیدسی صفر باشد باید همه مربعات تفاضل‌ها صفر باشند، در نتیجه دو نقطه بر هم منطبق هستند.
3. رابطه مثلثی برای فاصله اقلیدسی: اگر دو نقطه A به مختصات $$(x_1,y_1)$$ و نقطه B به مختصات $$(x_2,y_2)$$ وجود داشته باشند و همچنین $$(x_1-x_2)=x\; ; \;\;  (y_1-y_2)=y$$ در نظر گرفته شود، می‌توان نوشت:

$$D_{euc}^2(x,y)=x^2+y^2=(x+y)^2-2xy<(x+y)^2\rightarrow D_{euc}<x+y$$

که نشان می‌دهد فاصله اقلیدسی در نامساوی مثلثی صدق می‌کند. برطبق تصویر 2، نیز می‌توان مشاهده کرد که فاصله اقلیدسی در رابطه مثلثی صادق است.

مثال ۱

فرض کنید دو نقطه A و B در فضای دو بعدی با مختصات $$(2,4)$$ و $$(4,5)$$ وجود داشته باشد. فاصله این دو نقطه برحسب فاصله اقلیدسی برابر است با:

$$D_{euc}(A,B)=((2-4)^2+(4-5)^2)^\tfrac{1}{2}=\sqrt{(4+1)}=\sqrt{5}$$

نکته: اگر $$a_1, a_2,\ldots,a_n$$ نشانگر n نقطه در فضای p بعدی باشند، آنگاه مجموع فاصله اقلیدسی این نقاط از میانگیشان حداقل خواهد بود. یعنی:

$$\min (\sum D_{euc}(a_i,c))=\sum D_{euc}(a_i,\overline{a})$$

که منظور از $$\overline{a}$$ میانگین مولفه‌ای نقاط $$a_i$$‌ است. از این خاصیت در خوشه‌بندی تفکیکی «k-میانگین» (k-means) استفاده می‌شود و برای کمینه کردن فاصله نقاط خوشه حول یک نقطه مرکزی، میانگین نقاط را به عنوان مرکز انتخاب می‌کنند.

تابع فاصله منهتن

اگر به جای مربع فاصله بین مولفه‌ها، از قدر مطلق فاصله بین مولفه‌های نقاط استفاده شود، تابع فاصله را «منهتن» (Manhatan) می‌نامند. این نام به علت تقاطع منظم خیابان‌ها در محله منهتن نیویورک انتخاب شده است. البته این فاصله گاهی به نام «فاصله تاکسی» (Taxicab) یا «بلوک شهری» (City Block) نیز نامیده می‌شود.

فیلم آموزش فرایندها و قضایای مهم هندسه فینسلر (رایگان) در فرادرس

کلیک کنید

اگر x‌ و y دو نقطه با p مولفه (p بعدی) باشند، شیوه محاسبه فاصله منهتن به صورت زیر خواهد بود:

$$D_{man}=\sum_{i=1}^p|x_i-y_i|$$

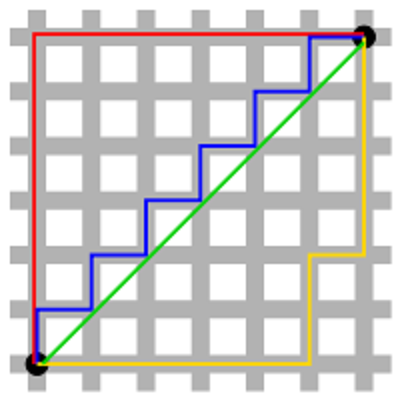
همانطور که در تصویر 3 دیده می‌شود، اگر محور افقی و عمودی به طول‌های برابر و مساوی با ۱ تقسیم شده باشند، بین دو نقطه سیاه رنگ، مسیرهای مختلفی با فاصله منهتن یکسان وجود دارد. خط‌های قرمز و آبی و زرد، مسیرهایی با فاصله منهتن ۱۲ بین این دو نقطه هستند،‌ در حالیکه خط سبز نشان دهنده فاصله اقلیدسی است که با طول برابر با $$6\sqrt2$$‌ کوتاه‌ترین مسیر را (در صورت وجود) نشان می‌دهد.

مثال ۲

براساس نقاط مربوط به مثال ۱، فاصله منهتن بین دو نقطه A و B به صورت زیر محاسبه می‌شود:

$$D_{man}(A,B)=(|2-4|+|4-5|)=2+1=3$$

همانطور که دیده می‌شود، فاصله منهتن برای این دو نقطه بزرگتر از فاصله اقلیدسی است. این واقعیت در تصویر ۳ نیز براساس مقایسه خط سبز و آبی قابل بررسی است. از آنجایی که خط سبز، نشانگر قطر هر مربع با اضلاع خاکستری است، بنا به نامساوی مثلثی از مجموع دو ضلع دیگر کوچکتر هستند.

میانه مولفه‌ای

از آنجایی که برای داده‌های چند بعدی نمی‌توان ترتیبی در نظر گرفت، میانه، به شکل‌های مختلفی تعریف شده است. یکی از این تعریف‌ها براساس فاصله منهتن صورت پذیرفته که به آن میانه مولفه‌ای می‌گویند.

تعریف میانه مولفه‌ای: اگر $$a_1, a_2,\ldots,a_n$$ نشانگر n نقطه در فضای p بعدی باشند، آنگاه «میانه مولفه‌ای» (Component-wise Median) برای aها که آن را با $$M_{comp}(a)$$ نشان می‌دهیم، نقطه‌ای است که مجموع فاصله منهتن نقاط از آن حداقل باشد. یعنی:

$$\min (\sum D_{man}(a_i,c))=\sum D_{_{man}}(a_i,M_{comp}(a))$$

نکته: از آنجایی که میانه مولفه‌ای، نقطه‌ای است که فاصله منهتن را کمینه می‌کند، در الگوریتم‌های خوشه‌بندی مانند PAM یا CLARA از میانه به عنوان مرکز هر خوشه استفاده می‌شود.

فاصله مینکوفسکی

فاصله مینکوفسکی براساس تحقیقات دانشمند ریاضی «هرمان مینکوفسکی» (Hermann Minkowski) که روس تبار بود، معرفی شد.

او با تعریف فاصله‌ جدیدش، حالت کلی‌تری از فاصله اقلدیسی و منهتن را برای اشکال محدب یا کوژ ایجاد کرد. اگر A و B دو نقطه در فضای p بعدی باشند،‌ فاصله مینکوفسکی برایشان به صورت زیر محاسبه می‌شود. پارامتر فاصله مینکوفسکی در اینجا d در نظر گرفته شده. فاصله مینکوفسکی با پارامتر d را به صورت  $$D_{mink}(A,B;d)$$ نشان می‌دهند.

$$D_{mink}(A,B;d)=(\sum_{i=1}^p|x_i-y_i|^d)^\tfrac{1}{d}$$

اگر مقدار d برابر با ۲ باشد،‌ فاصله مینکوفسکی به فاصله اقلیدسی تبدیل می‌شود. همینطور با انتخاب d=1 این فاصله همان فاصله منهتن خواهد بود. همچنین اگر $$d\to \infty$$ فاصله مینکوفسکی را فاصله چبیشف نیز می‌نامند و به صورت زیر تعریف می‌شود:

$$D_{mink}(A,B;\infty)=lim_{d \to \infty}(\sum_{i=1}^p|x_i-y_i|^d)^\tfrac{1}{d}=Max_{i=1}^p|x_i-y_i|$$

به این ترتیب فاصله چبیشف، بیانگر بزرگترین فاصله در بین فاصله‌های مولفه‌ها است.

بر همین اساس اگر $$d \to -\infty$$ فاصله مینکوفسکی حداقل فاصله‌ بین مولفه‌ها محسوب می‌شود. به این ترتیب خواهیم داشت:

$$D_{mink}(A,B;-\infty)=lim_{d \to -\infty}(\sum_{i=1}^p|x_i-y_i|^d)^\tfrac{1}{d}=Min_{i=1}^p|x_i-y_i|$$

مثال ۳

براساس مثال ۲ فاصله دو نقطه A و B براساس مقدارهای مختلف d در تصویر ۴ ترسیم شده است.

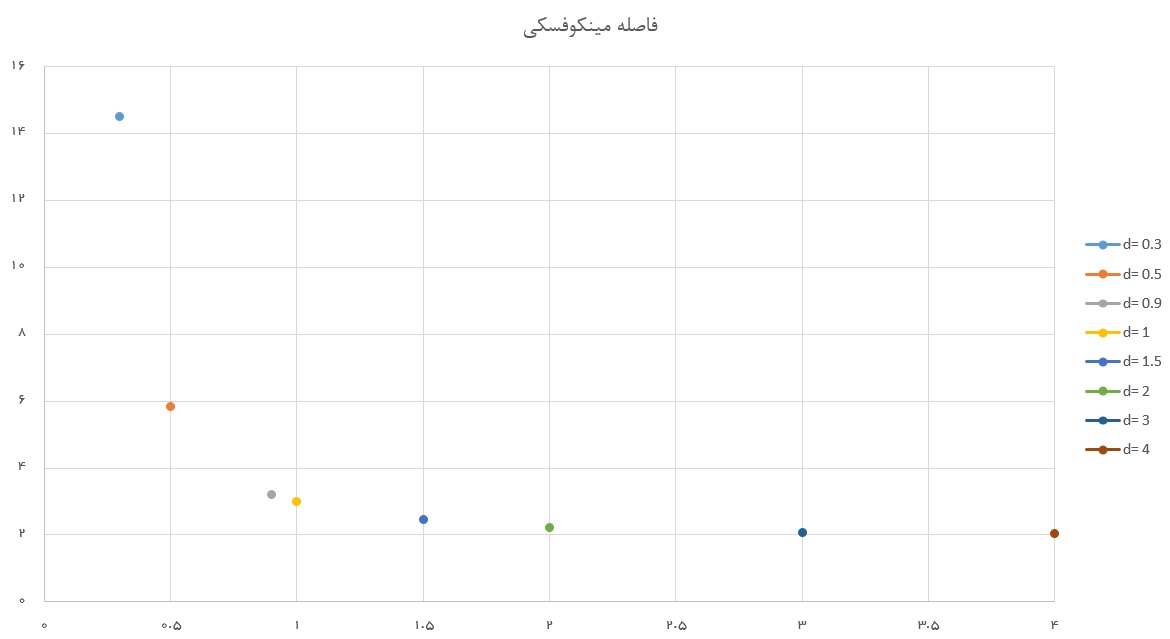
همانطور که مشخص است با افزایش مقدار d فاصله بین دو نقطه کوچکتر می‌شود.

نکته: برای مواقعی که d کوچکتر از ۱ باشد، فاصله مینکوفسکی در نامساوی مثلثی صدق نمی‌کند. در نتیجه در چنین حالتی فاصله مینکوفسکی یک فضای ورا-متریک (Ultra-metric) می‌سازد. فرض کنید دو نقطه‌ با مختصات (0,0)A و (1,1)B وجود دارد. فاصله مینکوفسکی بین این دو نقطه برحسب d<۱ برابر است با $$2^{\tfrac{1}{d}}$$‌ که از 2 بزرگتر است. حال فاصله هر کدام از این نقاط از نقطه (0,1)C برابر است با ۱ که نامساوی مثلثی را نقض می‌کند. اگر نامساوی مثلثی برقرار باشد، باید داشته باشیم:

$$2^d=D_{mink}(A,B;d)\leq D_{mink}(A,C;d)+D_{mink}(C,B;d)=1+1=2$$

که در واقع این نامساوی با توجه به اندازه‌ فاصله‌های گفته شده،‌ برقرار نیست.

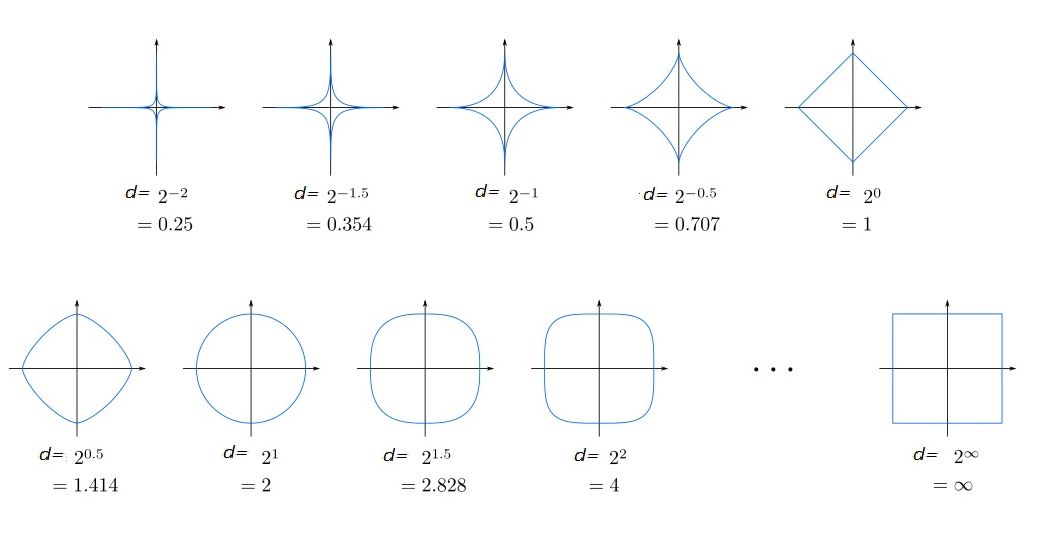
اگر مکان هندسی نقاط دو بعدی را در نظر بگیریم که از مرکز مختصات دکارتی دارای فاصله مینکوفسکی ثابت و برابر ۱ باشند، شکل‌های مختلفی به ازاء مقدارهای مختلف d، ترسیم خواهد شد. این منحنی‌ها در تصویر ۵ قابل مشاهده هستند. همانطور که دیده می‌شود، به ازاء مقدارهای d کوچکتر از ۱، شکل‌های ایجاد شده «کاو» (Concave) یا مقعر هستند و در حالتی که مقدار d بزرگتر از ۱ منظور شود، شکل‌ها به صورت «کوژ» (Convex) یا محدب در خواهند آمد.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
• آموزش خوشه بندی تفکیکی با نرم افزار R
• آموزش خوشه بندی سلسله مراتبی با SPSS

^^