افراز مجموعه ها – به زبان ساده

در مطالب قبلی مجله فرادرس، درباره مجموعه‌ها و موضوعات مرتبط با آن‌ها بحث کردیم. گفتیم که مجموعه‌ها، دسته‌هایی از اشیا و موجودات هستند که حداقل یک ویژگی مشترک دارند. این اشیا یا موجودات، عناصر، اجزا یا اعضای مجموعه نامیده می‌شوند. هیچ محدودیتی برای نوع اشیا وجود ندارد، اما در نظریه مجموعه‌ها، معمولاً با مجموعه‌هایی شامل عناصر مرتبط با ریاضیات سروکار داریم.

اِفراز در لغت به معنی تفکیک است که فرهنگستان زبان و ادب فارسی، آن را به‌عنوان معادل واژه «Partition» در ریاضیات برگزیده است. در این آموزش، «افراز مجموعه‌» (Set partitions) را بررسی می‌کنیم.

ابتدا به چند تعریف زیر توجه کنید:

مجموعه تهی (Empty set): مجموعه تهی، مجموعه‌ای است که هیچ عضوی ندارد. مجموعه تهی را با $$\phi$$ یا $$\{\}$$ نشان می‌دهند.

زیرمجموعه (Subset): یک زیرمجموعه، مجموعه‌ای است که همه اعضای آن از یک مجموعه دیگر به نام اَبَرمجموعه یا فوق مجموعه (superset) استخراج شده‌اند.

اجتماع مجموعه‌ها (Union of Sets): اجتماع (یا جمع) دو مجموعه، مجموعه‌ای است که اعضای آن، اعضای هر یک از دو مجموعه را با هم در بر می‌گیرد. اجتماع را با نماد $$\bigcup$$ بین دو مجموعه نشان می‌دهند. بدین ترتیب، اجتماع $$\{2, 3\}$$ و $$\{2,4 \}$$، مجموعه $$\{2, 3, 4\}$$ است.

اشتراک مجموعه‌ها (Intersection of Sets): اشتراک دو مجموعه، مجموعه‌ای است که شامل اعضای مشترک هر دو مجموعه باشد. اشتراک را با نماد $$\bigcap$$ بین دو مجموعه نشان می‌دهند. اشتراک $$\{2, 3\}$$ و $$\{2,4 \}$$، مجموعه $$\{2\}$$ است.

تعریف افراز

یک افراز (partition) از مجموعه A، مجموعه‌ای ناتهی، شامل زیرمجموعه‌هایی از مجموعه A است، به‌طوری که هر عضو از مجموعه A دقیقاً در یکی از این زیرمجموعه‌ها وجود داشته باشد.

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

به‌طور دقیق‌تر، افرازهای مجموعه A، خانواده‌ای از زیرمجموعه‌های A (که با S مشخص می‌شود) هستند اگر و تنها اگر شرایط زیر را داشته باشند:

1. این خانواده مجموعه، نباید شامل مجموعه تهی باشد ($$\phi \notin S$$).
2. مجموعه‌های خانواده S، مجموعه‌ A را پوشش دهد، یعنی $$\cup _{B\in S}B=A$$.
3. اگر اشتراک هر دو مجموعه از S‌ را بگیریم، به یک مجموعه تهی برسیم. به عبارت دیگر، اعضای مجموعه A باید دو به دو مجزا باشند، یعنی اگر L و M عضو S باشند و $$L\neq M$$، آن‌گاه $$L\cap M=\phi$$.

این افرازها، بخش (part)، بلوک (block) یا سلول (cell) نیز نامیده می‌شوند.

نوشتن افرازهای مجموعه

مجموعه چهارعضوی $$A=\{a, b, c, d\}$$ را در نظر بگیرید. با انجام مراحل زیر، می‌توان افرازهای این مجموعه را نوشت. برای نوشتن افرازها، باید ترکیبات مختلف آن‌ها را بنویسیم.

گام 1: ابتدا افرازهای 4 عضوی را می‌نویسیم که برابر با خود مجموعه است و در شرایط بالا صدق می‌کند:

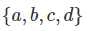
گام 2: اکنون، اجزای سه و یک عضوی را جدا می‌کنیم:

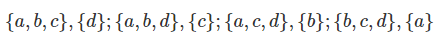
گام 3: مشابه روند قبل، اکنون، ترکیبات دو عضوی را می‌نویسیم:

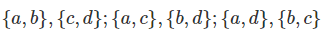
گام ۴: اکنون، ترکیبات 2، 1 و 1 عضوی را مشخص می‌کنیم: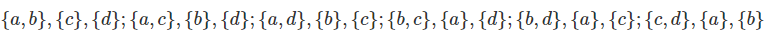

گام 5: می‌بینیم که فقط ترکیب‌های 1 عضوی برای نوشتن باقی می‌مانند:

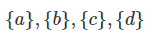
بنابراین، مشاهده می‌شود که 15 افراز ممکن برای یک مجموعه چهارعضوی دلخواه وجود دارد.

چند نکته

مجموعه $$\{x, y, z\}$$، شامل ۵ افراز زیر است:

• $$\{\{x\}, \{y\},\{z\}\}$$
• $$\{\{x,y\},\{z\}\}$$
• $$\{\{x,z\},\{y\}\}$$
• $$\{\{z, y\},\{x\}\}$$
• $$\{\{x, y, z\}\}$$

توجه کنید که:

• $$\{\{\}, \{x,z\}, \{y\}\}$$ نمی‌تواند یک افراز برای مجموعه باشد، زیرا شامل یک مجموعه تهی است.
• $$\{ \{x,z\}, \{y,z\}\}$$ نمی‌تواند یک افراز از مجموعه باشد، زیرا عضو z تکرار شده است.
• $$\{ \{x\}, \{y\}\}$$ نمی‌تواند یک افراز مجموعه باشد، زیرا یکی از سه عضو مجموعه در آن وجود ندارد.

مجموعه منفرده یا تک‌عضوی مانند $$\{a\}$$ فقط یک افراز دارد و آن هم، خودش است ($$\{\{a\}\}$$). همچنین، مجموعه تهی یکی افراز دارد که خودش است.

عدد بل

با استفاده از اعداد بل (Bell Numbers) می‌توان تعداد افرازهای ممکن یک مجموعه را محاسبه کرد. در حالت کلی، $$B_n$$ تعداد افرازهای مجموعه‌ای با n عضو است. فرمول مشخص ساده‌ای برای $$B_n$$ وجود ندارد. اما با کمک رابطه بازگشتی زیر می‌توان تعداد افرازهای ممکن یک مجموعه را به‌دست آورد:

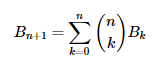
که در آن، $$\left(\begin{array}{c}n\\ k\end{array}\right)$$ نماد انتخاب k شی از n شی یا همان ترکیب است و با فرمول زیر محاسبه می‌شود:

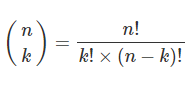
بنابراین، باید تعداد افرازهای ممکن مجموعه‌های کوچکتر از مجموعه مورد نظر را نیز محاسبه کنیم. برای مجموعه تهی، می‌دانیم که $$B_0=1$$. در نتیجه، مقدار $$B_1=1$$ به‌دست می‌آید و اگر همین‌طور ادامه دهیم، به $$B_4=15$$ می‌رسیم که برای مجموعه چهارعضوی $$A=\{a, b, c, d\}$$، آن‌ها را نوشتیم.

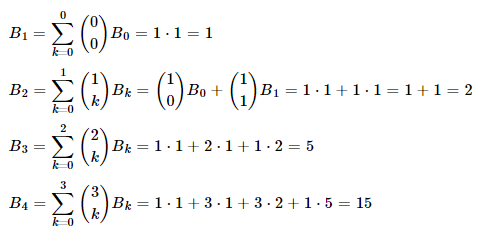
اگر علاقه‌مند به موضوعات مشابه و مرتبط به این مطلب هستید، پیشنهاد می‌کنیم آموزش‌های زیر را ببینید:

• مجموعه ها در ریاضیات – مفاهیم پایه
• اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده
• قوانین دمورگان در مجموعه ها — به زبان ساده
• استقرای ریاضی — به زبان ساده
• فهرست مطالب ریاضی وبلاگ فرادرس

^^