تصادفی بودن و آزمون گردش — به زبان ساده

در بیشتر روش‌های آماری که برمبنای «نمونه‌گیری» (Sample) شکل گرفته‌اند، فرض بر تصادفی بودن نمونه و مشاهدات است. در نتیجه اطمینان از تصادفی بودن نمونه‌ها از اهمیت زیادی برخوردار است. حتی در مباحث مربوط به رگرسیون نیز باید تصادفی بودن باقی‌مانده‌ها مورد بررسی قرار گرفته تا صحت مدل ایجاد شده مورد تایید قرار گیرد.

برای بررسی تصادفی بودن داده‌هایی که بخصوص در طی زمان جمع‌آوری شده‌اند، می‌توان از روش‌های ترسیمی و رسم نمودارهای کنترلی به مانند مباحث کنترل کیفیت آماری نیز استفاده کرد. ولی در اینجا هدف استفاده از تکنیک آزمون فرض آماری است که بتواند با توجه به روند و توالی مشاهدات، تصادفی بودن آن‌ها را تایید کند.

اگر نیاز دارید که با مفهوم آزمون آماری بیشتر آشنا شوید بهتر است مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری را مطالعه کنید. همچنین خواندن نوشتار فرایند تصادفی (Random Process) — مفاهیم اولیه نیز خالی از لطف نیست.

تصادفی بودن و آزمون گردش

فرض کنید مشاهداتی به صورت $$x_1,x_2,\cdots,x_n$$ در اختیار داریم. از طرفی اگر میانه این داده‌ها را $$m$$ بنامیم، می‌دانیم که نصف مقدارها از میانه بزرگتر و بقیه از میانه کوچکتر هستند. برای هر یک از مقادیر با استفاده از دو برچسب L و U مشخص می‌کنیم که آیا از میانه بزرگتر یا کوچکتر هستند.

فیلم آموزش فرایندهای تصادفی یا اتفاقی Stochastic Processes در فرادرس

کلیک کنید

بنابراین برای مثال اگر $$x_i$$ بزرگتر از $$m$$ باشد، برچسب آن را U در غیراینصورت L انتخاب می‌کنیم.

$$\large \begin{cases}L & x_i > m\\U & x_i \leq m\end{cases}$$

برای روشن شدن موضوع به جدول زیر توجه کنید.

به این ترتیب توالی از برچسب‌های U و L حاصل خواهد شد که نشان می‌دهد کدام یک از مقادیر از میانه بیشتر یا کمتر هستند.

گردش یا دو (RUN)

گردش یا دو برای داده‌های «دو وضعیتی» (Dichotomous) تعریف شده است. به این معنی که متغیری که برای بررسی یا شمارش گردش‌ها به کار می‌رود باید دو مقدار داشته باشد. تعداد توالی تکرارهای این مقدارها، تعداد گردش را نشان می‌دهد.

با توجه به جدول بالا، می‌توانیم گردش یا دو را تعریف کنیم. در این حالت روند تکرار برچسب‌ها را گردش یا دو می‌نامند. هرگاه در توالی برچسب‌ها به یک برچسب متفاوت برخورد کنیم یک گردش ایجاد شده است. بنابراین با توجه به روند برچسب‌های جدول بالا تعداد گردش‌ها برابر است با 2.

به نظر می‌رسد که کوچک بودن تعداد گردش نمی‌تواند دلیل مناسبی برای تصادفی بودن داده‌ها ارائه دهد. بنابراین قاعده تصمیم‌گیری در آزمون فرض تصادفی بودن داده‌ها را به صورت زیر می‌نویسم.

فرض صفر (تصادفی بودن داده) را رد می‌کنیم اگر تعداد گردش‌ها کوچک باشد. به بیان دیگر اگر $$r\leq c_1$$ فرض صفر رد می‌شود زیرا به نظر می‌رسد که یک روند در بین مشاهدات وجود دارد. البته مقدار $$c_1$$ را با توجه به توزیع $$r$$ و سطح معنی‌داری آزمون تعیین خواهیم کرد.

حال به یک مثال دیگر بپردازیم. واضح است که برای برچسب‌های زیر تعداد گردش‌ها برابر ۹ است.

به این ترتیب به نظر می‌رسد که یک حالت چرخشی بین مشاهدات وجود دارد. بنابراین به نظر می‌رسد که اگر تعداد گردش‌ها با توجه به تعداد مشاهدات خیلی زیاد باشد، «تصادفی بودن» (Randomness) داده‌ها مورد اشکال است. به این ترتیب اگر $$r\geq c_2$$ باشد، فرض تصادفی بودن داده‌ها رد می‌شود زیرا به نظر می‌رسد که حالت تناوبی در بین داده‌ها وجود دارد.

به این ترتیب می‌توانیم برای رد کردن فرض صفر که بیانگر تصادفی بودن داده‌ها است دو دلیل بیاوریم. اگر تعداد گردش‌ها از مقدار $$c_1$$ کمتر یا از $$c_2$$ بیشتر باشد، فرض تصادفی بودن داده‌ها را رد خواهیم کرد.

آماره R و توزیع گردش‌ها

همانطور که مشاهده کردید، گردش‌ها براساس داده‌های دو وضعیتی ساخته می‌شوند و مشخص است که این برچسب‌ها یا داده‌های دو وضعیتی دارای توزیع دوجمله‌ای (Binomial Distribution) هستند.

فرض کنید که تعداد Lها برابر با $$n_1$$ و  تعداد Uها نیز برابر با $$n_2$$ است بطوری که $$n_1+n_2=n$$. با توجه به اینکه متغیر تصادفی R که تعداد گردش‌ها است، یک متغیر تصادفی گسسته با تکیه‌گاه متناهی است، می‌توانیم تابع احتمال آن را برحسب مفهوم احتمال براساس فراوانی نسبی بدست آوریم.

اگر r=2k یعنی تعداد گردش‌ها زوج باشد، احتمال از طریق رابطه زیر محاسبه می‌شود.

$$\large P(R=2k) = \dfrac{2{n_1-1 \choose k-1}{ n_2-1 \choose k-1}}{n_1+n_2 \choose n_1}$$

و اگر تعداد گردش‌ها فرد یعنی r=2k+1 باشد رابطه محاسباتی برای احتمال گردش‌ها به صورت زیر خواهد بود.

$$\large P(R=2k+1) = \dfrac{{n_1-1 \choose k}{ n_2-1 \choose k-1}+{n_2-1 \choose k}{ n_1-1 \choose k-1}}{n_1+n_2 \choose n_1}$$

مثال ۱

فرض کنید توالی از برچسب‌ها به صورت زیر در اختیارتان قرار گرفته است. می‌خواهیم تشخیص دهیم که با چه میزان سطح آزمون، می‌توان تصادفی بودن آن‌ها را تعیین کنیم.

$$ \large U,U,U,U,U,L,L,L,L,L,L,U,L,U,L,U$$

مطابق با رابطه بالا احتمالات را برای چند وضعیت مختلف محاسبه می‌کنیم.

$$\large P(R=2)=\dfrac{2{7 \choose 0}{7 \choose 0}}{16 \choose 8}=\dfrac{2{7 \choose 7}{7 \choose 7}}{16 \choose 8}=P(R=16)=\dfrac{2}{12870}$$

$$\large P(R=3)=\dfrac{{7 \choose 1}{7 \choose 0}+{7 \choose 1}{7 \choose 0}}{16 \choose 8}=\dfrac{{7 \choose 7}{7 \choose 6}}{16 \choose 8}=P(R=15)=\dfrac{14}{12870}$$

$$\large P(R=4)=\dfrac{2{7 \choose 1}{7 \choose 1}}{16 \choose 8}=\dfrac{2{7 \choose 6}{7 \choose 6}}{16 \choose 8}=P(R=14)=\dfrac{98}{12870}$$

در نتیجه اگر بخواهیم در سطح آزمون حدود 0.018 تصمیم بگیریم ناحیه بحرانی به صورت زیر در خواهد آمد.

$$\large \alpha = P(R\leq 4)+P(R\geq 14)=2\times \dfrac{2+14+98}{12870}=\dfrac{228}{12870}=0.018$$

بنابراین چون تعداد گردش‌ها در این داده‌ها برابر است با ۷ و از ۱۴ کوچکتر و از ۲ بزرگتر است، فرض صفر که بیانگر تصادفی بودن داده‌ها است، در سطح آزمون 0.02 رد نمی‌شود. به این ترتیب خواهیم گفت که براساس این نمونه شواهدی مبنی بر رد فرض صفر وجود ندارد.

هنگام نمونه‌گیری اگر تعداد نمونه‌ها فرد باشد، میانه را می‌توان به گروه بالایی نسبت داد در این حالت $$n_2=n_1+1$$. اگر مقدار میانه به صورت گره (مقدار تکراری برای میانه) باشد، میانه و مقدارهای برابر با آن را در گروه بالایی (U) قرار داده ومحاسبات را پی می‌گیریم.

البته برای توزیع مجانبی آماره آزمون نیز هنگامی که مشاهدات زباد باشند، با کمک توزیع نرمال می‌توان آزمون را انجام داد. اگر $$R$$ تعداد گردش‌ها، $$\overline{R}$$ نیز متوسط تعداد گردش‌ها و $$S^2_R$$‌ نیز واریانس گردش‌ها باشد، آماره آزمون برای گردش‌ها یعنی $$Z$$ توسط رابطه زیر محاسبه می‌شود.

$$\large Z=\dfrac{R-\overline{R}}{S_r}\sim N(\overline{R}, S^2_R)$$

$$\large \overline{R}=\dfrac{2n_1n_2}{n_1+n_2}+1$$

$$\large S^2_R=\dfrac{2n_1n_2(2n_1n_2-n_1-n_2}{(n_1+n_2)^2(n_1+n_2-1)}$$

به این ترتیب اگر در آزمون «دو طرفه» (Two Tailed) برای گردش‌ها با توجه به فرض صفر و فرض مقابل زیر، با توجه به صدک توزیع نرمال، اگر مقدار $$|Z| > Z_{1-\frac{\alpha}{2}}$$ باشد، فرض صفر را رد کرده و رای به غیرتصادفی بودن داده‌ها خواهیم داد.

$$\large \begin{cases}H_0: & Randomness\\H_1: & Non-Randomness\end{cases}$$

نکته: همانطور که اشاره شد، در اینجا، به عنوان محل برش یا تعیین برچسب‌ها از میانه استفاده شد. به این شکل خواهیم گفت که داده‌ها حول میانه به طور تصادفی پراکنده هستند. ممکن است این محل برش براساس میانگین، میانه یا هر مقدار دلخواه دیگری تعیین شود. به این ترتیب خواهیم گفت داده‌ها حول میانگین یا نما تصادفی هستند.

در ادامه به منظور اجرای آزمون گردش از نرم‌افزار SPSS استفاده خواهیم کرد و به کمک آن تصادفی بودن داده‌های مربوط به یک مثال را مورد بررسی قرار می‌دهیم.

آزمون گردش در SPSS

همانطور که گفته شد، آزمون گردش برای مشخص کردن تصادفی بودن داده‌ها بسیار مناسب است. یکی از اصول در تغییرات فرآیند تولید، تصادفی بودن آن است که در مباحت کنترل کیفیت مورد بررسی قرار می‌گیرد. در داده‌هایی که در تصویر زیر می‌بینید وزن ۱۶ بسته ماکارونی برحسب گرم ثبت شده است.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

قرار است که دستگاه سنجش وزن مورد بازبینی قرار گیرد. با استفاده از آزمون گردش می‌خواهیم مشخص کنیم که آیا دستگاه ترازو احتیاج به کالیبراسیون دارد یا تفاوت در وزن‌ها، ناشی از خطای تصادفی فرآیند تولید یا اندازه‌گیری است.

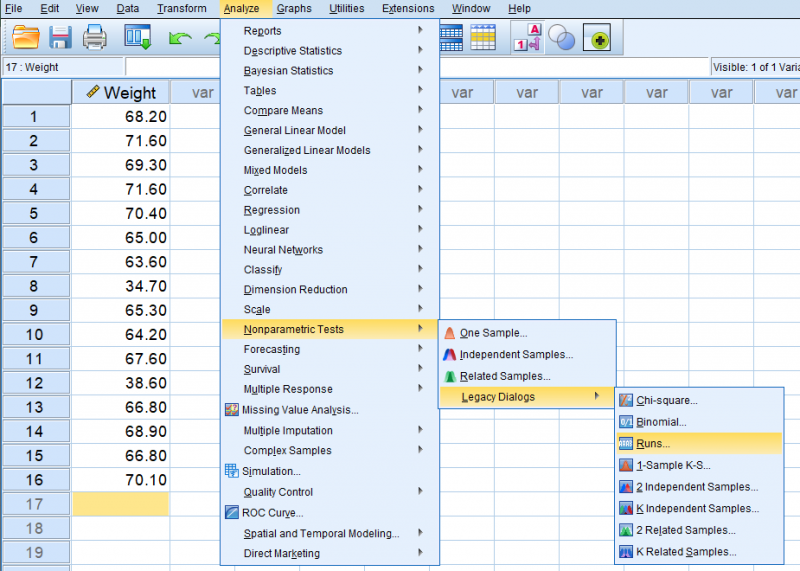
همانطور که در تصویر می‌بینید روند دسترسی به این فرمان مشخص شده است. برای انجام آزمون کافی است که متغیر مورد نظرتان را در کادر Variable List قرار دهید. اگر می‌خواهیم مبنای تفکیک برای تصادفی بودن داده‌ها، میانه در نظر گرفته شود گزینه Median را در کادر Cut Point مشخص کنید. از دیگر گزینه‌های این بخش می‌توانید میانگین (Mean)، نما (Mode) و حتی مقداری دلخواه (Custom) را برای تفکیک داده‌ها به دو بخش معرفی کنید.

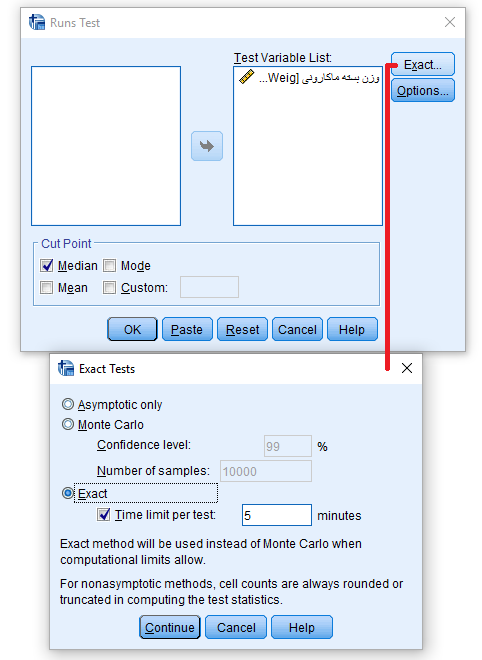
نکته: اگر می‌خواهید «آزمون دقیق» (Exact Test) و براساس توزیع دقیق آماره R انجام گیرید، دکمه Exact را در پنجره اصلی انتخاب و تنظیمات را در پنجره Exact Tests مانند تصویر بالا درآورید. با فشردن دکمه Continue به پنجره اولیه باز خواهید گشت.

اگر می‌خواهید تنظمیات دیگری که مربوط به داده‌های گمشده و یا نمایش آمار توصیفی و چندک‌های داده‌ها است را  فعال کنید از دکمه Options‌ استفاده کنید. در پنجره اصلی، با فشردن دکمه OK محاسبات انجام شده و نتیجه مطابق با تصویر زیر ظاهر خواهد شد.

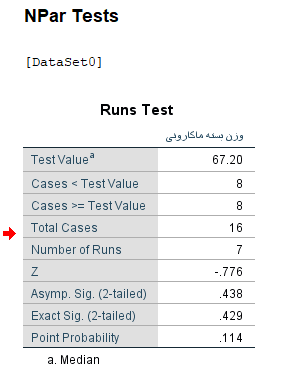
در ستون اول از سمت چپ، اسامی هر یک از بخش‌های خروجی و در ستون دوم مقدارهای هر یک ظاهر شده است. جدول زیر به معرفی این بخش‌ها پرداخته است.

همانطور که در جدول خروجی مشاهده می‌کنید با توجه به اینکه مقدار Sig=$$0.429$$ بزرگتر از احتمال خطای نوع اول $$0.05$$ است، دلیلی برای رد فرض صفر وجود ندارد. بنابراین نمونه، گواهی بر تصادفی بودن داده‌ها است و نیازی به کالیبره کردن دستگاه ترازو نیست.

اگر از پنجره Syntax بخواهید دستورات را وارد کنید کافی است از کد زیر بهره ببرید. نتیجه با اجرای این دستورات به مانند قبل خواهد بود.

1DATASET ACTIVATE DataSet0.
2NPAR TESTS
3  /RUNS(MEDIAN)=Weight
4  /MISSING ANALYSIS
5  /METHOD=EXACT TIMER(5).

البته می‌توانید این آزمون را در محیط «نمایشگر مدل» (Model Viewer) نیز اجرا و نتایج را نمایش دهید. کافی است که از مسیر زیر به پنجره اجرای آزمون گردش دسترسی پیدا کنید.

Analyze->Nonparamteric Tests- > One Sample

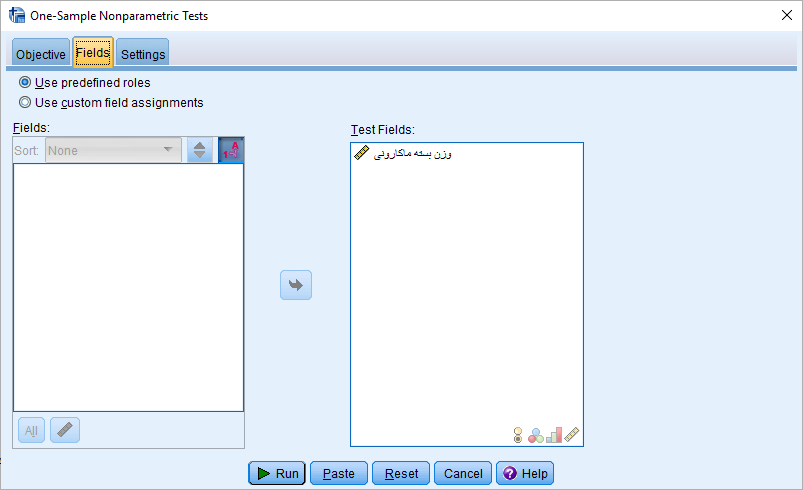
پنجره‌ One-Sample Nonparamteric Tests به مانند زیر ظاهر خواهد شد. کافی است که تنظیمات را مطابق با تصویر انجام دهید.

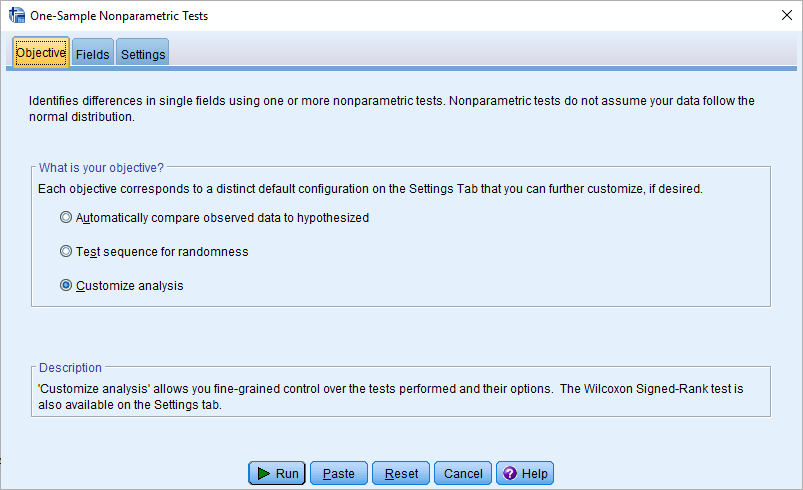
از آنجایی که می‌خواهید خارج از حالت خودکار SPSS به صورت دستی آزمون Run را انجام دهید، گزینه Customize analysis را انتخاب کنید. البته اگر گزینه دوم یعنی test sequence for randomness را هم که به معنی «آزمون توالی تصادفی» است، انتخاب کنید نتیجه مشابه‌ای خواهید گرفت. با انتخاب برگه Fields متغیرهای مورد نظرتان را در کادر Test Fields قرار دهید. البته اگر نقش (Roles) هر متغیر به درستی تعریف شده باشند، SPSS قادر به انتخاب متغیر صحیح به صورت خودکار خواهد بود. در اینجا از متغیر وزن بسته ماکارونی (Weight) استفاده شده است.

با انتخاب برگه Settings آخرین گام در تنظیمات اجرای آزمون گردش را انجام خواهید داد.

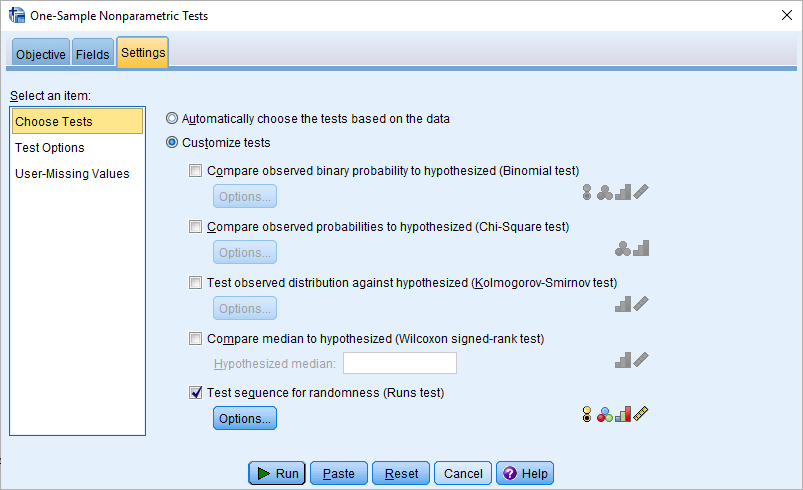
با توجه به انتخابی که در قسمت یا برگه Objective انجام داده‌اید، SPSS گزینه Test Sequence را انتخاب کرده است. مشخص است که نوع آزمون به درستی تعیین شده است. هر یک از گزینه‌های سمت چپ کادر Select and item با توجه به نوع آزمون انتخابی، اختیاراتی را برای انجام آزمون ظاهر می‌کند. برای مثال با انتخاب Test Options قادر هستید، «میزان خطا» (Significant Level) یا «سطح اطمینان» (Confidence Interval) آزمون و فاصله اطمینان را تعیین کنید. یا نسبت به نقش مقدارهای گمشده (Missing) در آزمون‌هایی با چند متغیری تصمیم‌گیری کنید.

فیلم آموزش حسابان حرکت براونی در فرایندهای تصادفی (رایگان) در فرادرس

کلیک کنید

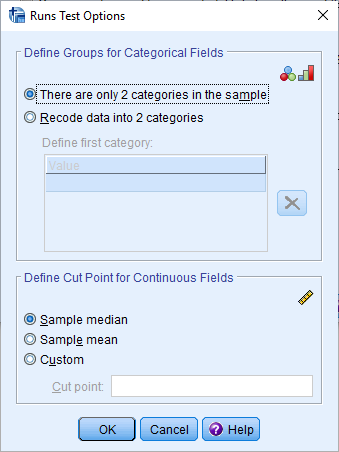
اگر دکمه Options را که در انتهای پنجره دیده می‌شود،‌ کلیک کنید، امکاناتی که مختص آزمون گردش است، ظاهر خواهد شد. برای مثال با انتخاب Sample mean، به عنوان نقطه برش برای «متغیرهای پیوسته» (Continuous Fields) از میانگین استفاده خواهد شد. همچنین می‌توانید به طور دستی گروه‌ها را مشخص کنید. با انتخاب گزینه Recode data into 2 categories مقدارهایی که باید متعلق به گروه اول باشند را در لیست Define first category وارد کرده و دکمه OK را بزنید.

پس از انجام همه تنظیمات و گزینه‌ها در پنجره اصلی با فشردن دکمه Run اجرای آزمون صورت خواهد گرفت و خروجی به شکل زیر خواهد بود.

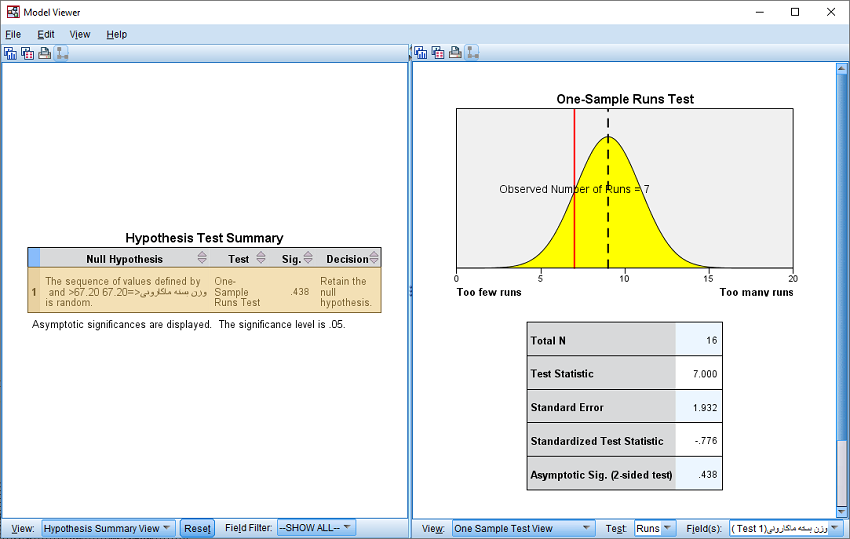
در کادر سمت چپ، مشخص است که مقدار Sig=0.438 در اینجا با حالت قبل برای توزیع مجانبی آماره آزمون، برابر است. از طرفی در ستون Decision نیز مشخص است که نتیجه اجرای آزمون تایید فرض صفر است. البته توجه داشته باشید که نوع و فرض صفر مربوط به آزمون در ستون Null Hypothesis نوشته شده است. در کادر سمت راست نیز نمودار مربوط به توزیع آماره گردش‌ها یعنی R ترسیم شده است. میانگین توزیع بوسیله خط چین مشکی و مقدار محاسبه شده گردش نیز با خط قرمز رنگ روی نمودار دیده می‌شود. مقدار آماره و انحراف استاندارد آماره و مقدار Sig نیز در جدول زیرین قابل مشاهده است. بالای هر کادر در این پنجره دکمه‌هایی برای تهیه نسخه‌برداری از نمودارها یا داده‌ها و چاپ نتایج وجود دارد.

نکته: توجه داشته باشید که با توجه به تعداد داده‌ها این روش از توزیع مجانبی (Asymptotic Distribution) آماره آزمون استفاده کرده است. در نتیجه خروجی‌های مربوط به Sig همه برحسب توزیع مجانبی محاسبه شده است.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• متغیر دو وضعیتی (Dichotomous) در SPSS — راهنمای کاربردی
• آزمون دو جمله‌ ای (Binomial Test) در SPSS — راهنمای کاربردی

^^