فرادرسفرایند تصادفی (Random Process) — مفاهیم اولیه
در تئوری احتمالات، «فرایند تصادفی» (Random Process)، براساس دنباله‌ای از متغیرهای تصادفی شکل می‌گیرد که برحسب یک شاخص دارای ترتیب رخداد هستند. معمولا این شاخص را اندیس زمانی در نظر می‌گیرند. به این ترتیب مقدار متغیر تصادفی هم به زمان و هم به توزیع احتمالی متغیر تصادفی وابسته است. در بیشتر مواقع، فرایند تصادفی به بررسی پدیده‌های تصادفی می‌پردازد که برحسب زمان اندیس‌گذاری شده‌اند یا به بیان دیگر تغییراتی وابسته به زمان دارند. فرایندهای تصادفی در زمینه‌های مختلف علوم بخصوص در زیست‌شناسی (فرایند رشد باکتری‌ها در طول زمان)، فیزیک (حرکت براونی ملکول‌ها و فیزیک کوانتم) و حتی بازار سهام و تجارت به کار می‌روند.
در این نوشتار به معرفی فرایند تصادفی و بعضی از گونه‌های آن خواهیم پرداخت که در شاخه‌های مختلف علم کاربرد دارند. برای درک بهتر این مطلب بهتر است نوشتارهای متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و آزمایش تصادفی، پیشامد و تابع احتمال را از قبل مطالعه کرده باشید. همچنین خواندن مطلب متغیر تصادفی و توزیع نمایی — به زبان ساده نیز خالی از لطف نیست.
فرایند تصادفی (Random Process)
یک فرآیند تصادفی بر اساس دنباله‌ای از متغیر تصادفی مثل $$X$$ با تکیه‌گاهی به نام $$S$$ شناخته می‌شود که توسط مجموعه شاخص $$T$$، اندیس‌گذاری شده است.
چنین فرآیندی را به صورت دنباله‌ای از متغیر تصادفی به شکل زیر نشان می‌دهند.
$$\large \{X(t): t\in T\}$$
در اکثر کاربردها، منظور از مجموعه شاخص، زمان‌هایی است که فرایند در آن جریان دارد. به این ترتیب فرایندهای تصادفی را به دو گروه فرایندهای تصادفی زمان گسسته و یا زمان پیوسته تقسیم‌بندی می‌کنند. در ادامه به معرفی ویژگی‌های فرایندهای تصادفی خواهیم پرداخت.
فضای حالت (State Space)
فضای حالت بیان کننده فضا یا مجموعه مقدارهایی است که متغیر تصادفی مربوط به فرآیند تصادفی خواهد داشت. این فضای حالت را با $$S$$ نشان می‌دهند.
برای مثال اگر فرآیند تصادفی را به صورت پرتاب تاس در طول زمان و مشاهده عدد ظاهر شده در نظر بگیریم، فضای حالت برابر است با:
$$\large S=\{1,2,3,4,5,6\}$$
با توجه به پیوسته یا گسسته بودن تکیه‌گاه متغیر تصادفی، فرایند را گسسته یا پیوسته می‌گویند.
مجموعه شاخص (Index Set)
معمولا مجموعه شاخص بیانگر زمانی است که متغیر تصادفی مشاهده شده است. البته ممکن است مجموعه شاخص در فضای دو بعدی (زمان و مکان) نیز به کار رود ولی میتوان از خصوصیات جالب این مجموعه، به وجود ترتیب در عناصر آن اشاره کرد. به این ترتیب اگر زمان گسسته را ملاک برای مجموعه شاخص در نظر بگیریم، خواهیم داشت:
$$\large T=\{0,1,2,3,\cdots\}$$
با توجه به پیوسته یا گسسته بودن مجموعه شاخص (زمان) فرآیند را زمان گسسته یا زمان پیوسته می‌گویند.
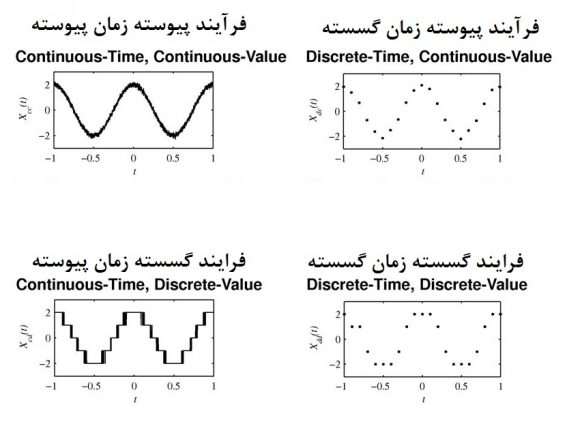
به این ترتیب چهار حالت برای یک فرایند تصادفی با توجه به مجموعه شاخص و فضای حالت میتوان تشخیص داد.
- فرایند گسسته زمان گسسته: مثالی از این فرایند می‌تواند فرایند برنولی باشد که مجموعه مقادیر متغیر تصادفی گسسته و زمان (تعداد پرتاب‌ها) نیز گسسته است.
- فرایند گسسته زمان پیوسته: این حالت را میتوان در علوم مخابرات مشاهده کرد. قطعی یا عدم قطع پیام در زمان (پیوسته) مطلوب چنین فرایندی است. مشخص است که مقدار متغیر تصادفی ۰ و ۱ است در حالیکه زمان به صورت پیوسته تغییر می‌یابد.
- فرایند پیوسته زمان گسسته: اگر میزان اشعه رادیواکتیو یک گرم ماده اورانیوم را در دوره‌های مشخصی اندازه‌گیری کرده‌ایم. چنین فرآیندی را میتوان پیوسته زمان گسسته در نظر گرفت.
- فرایند پیوسته زمان پیوسته: تغییرات دما در طول شبانه روز در یک منطقه ثبت می‌شود. با توجه به پیوستگی متغیر دما و زمان، چنین فرآیندی پیوسته زمان پیوسته است.
قانون فرآیند (Law of Process)
فرض کنید یک فرآیند تصادفی به صورت $$X:\Omega \rightarrow S^T$$ نوشته شود که در آن فضای احتمال به صورت $$(\Omega, F ,P)$$ در نظر گرفته شده است. قانون فرآیند تصادفی $$X$$ به صورت زیر تعریف می‌شود.
$$\large P(X_{n+1}=x|X_1=x_1,X_2=x_2,\cdots,X_n=x_n)$$
به این ترتیب میتوان احتمال رخداد $$X_{n+1}=x$$ را برحسب مقادیر قبلی فرایند تعیین کرد. در حقیقت این احتمال نشانگر تابع توزیع احتمال فرایند تصادفی است. با دانستن قانون فرایند، فضای حالت و مجموعه شاخص، میتوان احتمالات مربوط به رخدادهای مختلف در فرآیند را مشخص کرد.
مسیر (Path)
اگر تمرکز را بر یکی از نتایج متغیر تصادفی معطوف کنیم و تغییرات آن را در زمان‌های مختلف در نظر بگیریم، یک مسیر ساخته‌ایم. به این ترتیب اگر T را مجموعه شاخص و S را فضای حالت در نظر بگیریم، مسیر تابعی است که مقادیر T را به S می‌برد. در نتیجه داریم:
$$\large X(\cdot ,\omega ):T\rightarrow S$$
توجه داشته باشید که منظور از $$\omega$$ پیشامد ساده یا عناصر فضای پیشامد است که متغیر تصادفی $$X$$ براساس آن محاسبه شده است. به این ترتیب اگر $$X$$ متغیر تصادفی باشد، $$X_1=x_1,X_2=x_2,\cdots,X_n=x_n$$ می‌تواند یک مسیر را نشان دهد.
در ادامه به معرفی چند فرآیند تصادفی که البته پر کاربرد نیز هستند می‌پردازیم.
فرایند برنولی (Bernoulli Process)
معمولا فرایند برنولی را براساس پرتاب یک سکه اریب (ناسالم) معرفی می‌کنند که شانس مشاهده شیر در آن با $$p$$ و مشاهده خط نیز با $$1-p$$ در هر پرتاب برابر است. فرض بر این است که پرتاب‌ها نیز مستقل از یکدیگر بوده و شانس مشاهده شیر یا خط در همه پرتاب‌ها یکسان است (سکه در پرتاب‌ها دچار تغییر نمی‌شود).
مشخص است که فضای حالت در این فرایند به صورت $$S=\{0,1\}$$ و با در نظر گرفتن زمان گسسته مجموعه شاخص به شکل $$T=\{0,1,2,3,4,\cdots\}$$ تعریف می‌شوند. برای مثال در پرتاب یک سکه میتوان چنین فرآیندی را به صورت زیر نشان داد.
$$\large \{1,1,0,1,0,1,0,1,0,0,0,1,0,0,1,0,\cdots\}$$
به این ترتیب اگر 0 نشانگر خط بودن و 1 نیز شیر بودن سکه را نشان دهد، مشخص است که در اولین و دومین وضعیت زمانی (پرتاب) نتیجه مشاهده شیر و در پرتاب سوم خط و در پرتاب چهارم شیر و ... بوده است. نمودار زیر بیانگر فرایند برنولی با چنین حالتی است.
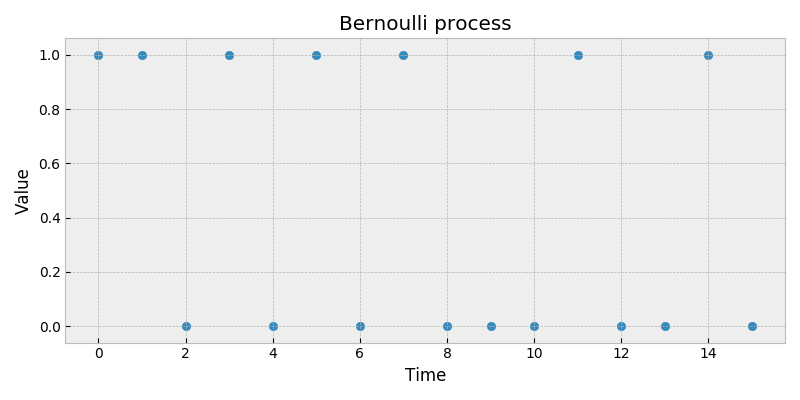
همانطور که دیده می‌شود مجموعه مقادیر فرآیند فقط ۱ و ۰ است که در طول زمان به صورت گسسته ظاهر شده است. بنابراین چنین فرآیندی به گروه فرایندهای گسسته زمان گسسته تعلق دارد.
قدم‌زدن تصادفی (Random Walk)
در سال 1905 کارل پیرسون (Karl Pearson) به مفهوم قدم‌زدن تصادفی اشاره کرد. از یافته‌های مرتبط با فرایند قدم زدن‌های تصادفی در شرط‌بندی نیز استفاده می‌شود. در سال 1919 و 1921 «جورج پولیا» (George Polya) مقالاتی در مورد قدم‌زدن‌های تصادفی در فضای nبعدی با مجموعه شاخص (زمان) گسسته مطرح کرد. او احتمال بازگشت به نقطه شروع را در چنین حالتی مطالعه و مطرح ساخت. نتیجه این مطالعات نشان داد که در فضای ۱ و ۲ بعدی با در نظر گرفتن احتمال‌های برابر در حرکت به نقاط، احتمال بازگشت به نقطه شروع برابر با ۱ و در ابعاد ۳ و بیشتر برابر با صفر است.
حرکت براونی یا فرآیند وینر (Brownian Motion or Wiener Process)
حرکت براونی و فرآیند وینر ریشه در آمار، امور مالی و فیزیک دارد. این فرآیند به صورت یک فرآیند زمان پیوسته در نظر گرفته می‌شود. از مولفه‌‌های مشخص برای چنین فرآیندی میتوان به مستقل بودن مقدار گام‌ها یا فاصله نقطه‌های مربوط به فرآیند نام برد. همچنین در این فرایند تصادفی، میزان افزایش یا طول گام‌ها براساس توزیع نرمال تعیین می‌شود. میانگین این توزیع برابر با صفر و واریانس آن نیز در همه گام‌ها ثابت است. این فرآیند توسط «نوربرت وینر» (Norbert Wienner) مورد مطالعه قرار گرفت و بعدها در فیزیک بسیار به کار گرفته شد به طوری که در سال 1905، آلبرت اینشتین (Albert Einstein) در این باره مقاله‌ای به چاپ رساند. از آنجایی که این فرایند می‌تواند در فیزیک و حرکت مولکول‌ها که به حرکت براونی (Brownian Motion) شهرت دارد به کار گرفته شود، گاهی به نام فرآیند حرکت براونی نیز خوانده می‌شود.
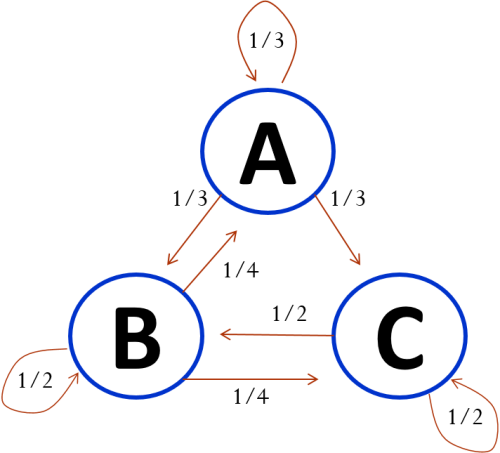
زنجیره یا فرآیند مارکف (Markov Chain)
در ابتدای قرن بیستم، «آندری مارکف» (Andry Markov) به دنباله‌های تصادفی مستقل علاقمند شد. او در سال 1906 اولین مقاله خود را در حوزه زنجیره مارکف یا فرآیند مارکف تهیه کرد. او نشان داد که تحت شرایط مشخصی، میانگین نتایج یک زنجیره مارکف به مقدار ثابتی میل خواهد کرد.
در فرآیند یا زنجیره مارکف، وجود «خاصیت عدم حافظه» (Memory Less Property) از اهمیت زیادی برخوردار است. به این معنی که احتمال قرارگیری در محل بعدی فقط به موقعیت فعلی بستگی دارد و به مسیری که برای رسیدن به موقعیت حال حاضر طی شده وابسته نیست. این وضعیت در قانون احتمال این فرآیند دیده می‌شود.
$$\large P(X_{n+1}=x|X_1=x_1,X_2=x_2,\cdots,X_n=x_n)=P(X_{n+1}=x|X_n=x_n)$$
مشخص است که در اینجا منظور از $$P(X_{n+1}=x|X_n=x_n)$$ احتمال شرطی مشاهده x برای متغیر تصادفی در زمان یا موقعیت n+1 است به شرط آن که مقدار متغیر تصادفی در زمان یا موقعیت n برابر با $$x_n$$ باشد. پس به نظر می‌رسد که مشخصه فرآیند مارکف این است که احتمال برای موقعیت بعدی متغیر تصادفی فقط به موقعیت حال حاضر آن بستگی دارد و مسیر رسیدن به موقعیت جاری در این احتمال موثر نیست.
اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
- آموزش آمار و احتمال مهندسی
- مجموعه آموزش‌های نرم‌افزارهای آماری
- احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
- آزمایش تصادفی، پیشامد و تابع احتمال
- متغیر تصادفی و توزیع پواسن — به زبان ساده
- متغیر تصادفی و توزیع هندسی — به زبان ساده
^^
سلام و وقت بخیر، فرآیند وینر را در کدام نرم افزار میتوان اجرا کرد؟