برنامه محاسبه ترانهاده ماتریس – به زبان ساده
در مطلب «ترانهاده ماتریس — به زبان ساده» مفهوم ماتریس ترانهاده یا ترانهاده ماتریس (Matrix Transpose) بیان و روش محاسبه آن تشریح شده است. در این مطلب، روش نوشتن برنامه محاسبه ترانهاده ماتریس بیان و پیادهسازی آن در زبانهای برنامهنویسی گوناگون شامل ++C، «جاوا» (Java)، «پایتون» (Python)، «سیشارپ» (#C) و «پیاچپی» (PHP) انجام شده است. ترانهاده یک ماتریس با تغییر سطرها به ستونها وستونها به سطرها به دست میآید.

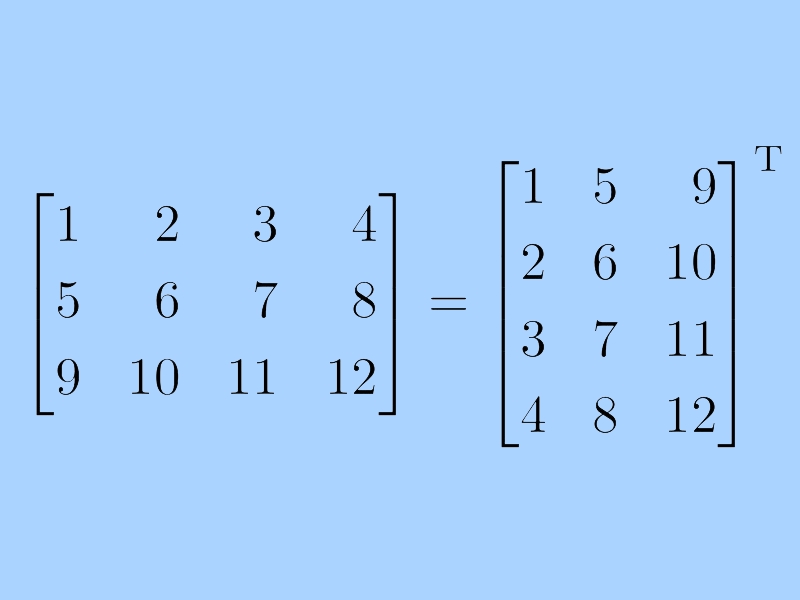
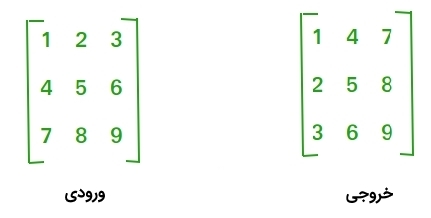
در انیمیشن زیر نیز روش محاسبه ترانهاده ماتریس نمایش داده شده است:

به عبارت دیگر، ترانهاده ماتریس []A با تغییر [A[i][j به [A[j][i محاسبه میشود. برنامه زیر، ترانهاده ماتریس [][]A را پیدا و نتیجه را در [][]B ذخیره میکند. میتوان N را برای ابعاد گوناگون تغییر داد.
برنامه محاسبه ترانهاده ماتریس در ++C
برنامه محاسبه ترانهاده ماتریس در جاوا
برنامه محاسبه ترانهاده ماتریس در پایتون ۳
برنامه محاسبه ترانهاده ماتریس در #C
برنامه محاسبه ترانهاده ماتریس در PHP
خروجی قطعه کدهای بالا، به صورت زیر است.
Result matrix is 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
برای ماتریس مربعی، میتوان از برنامههایی که در ادامه آمده جهت پیدا کردن ترانهاده ماتریس [][]A و ذخیره آن در [][]B استفاده کرد.
برنامه محاسبه ترانهاده ماتریس مربعی در ++C
برنامه محاسبه ترانهاده ماتریس مربعی در جاوا
برنامه محاسبه ترانهاده ماتریس مربعی در پایتون
برنامه محاسبه ترانهاده ماتریس مربعی در #C
برنامه محاسبه ترانهاده ماتریس مربعی در PHP
خروجی قطعه کدهای بالا به صورت زیر است.
Result matrix is 1 2 3 1 2 3 1 2 3 1 2 3
برای محاسبه ترانهاده ماتریس مربعی به صورت در محل (در جا) میتوان از روش زیر استفاده کرد.
برنامه محاسبه ترانهاده ماتریس مربعی به صورت در محل در ++C
برنامه محاسبه ترانهاده ماتریس مربعی به صورت در محل در جاوا
برنامه محاسبه ترانهاده ماتریس مربعی به صورت در محل در پایتون ۳
برنامه محاسبه ترانهاده ماتریس مربعی به صورت در محل در #C
برنامه محاسبه ترانهاده ماتریس مربعی به صورت درجا در PHP
خروجی قطعه کدهای بالا به صورت زیر است.
Modified matrix is 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش برنامهنویسی C++
- مجموعه آموزشهای ریاضیات
- معرفی تکنیکهای مرتبسازی (Sorting Techniques) — ساختار داده و الگوریتم ها
- مرتبسازی درجی (Insertion Sort) — به زبان ساده
- پیچیدگی زمانی الگوریتمهای مرتبسازی با نماد O بزرگ — به زبان ساده
^^












