تنش اصلی و تنش برشی ماکسیمم – آموزش جامع
در مبحث «تنش صفحهای» به معرفی مفاهیم مرتبط با این تنش و معادلات تبدیل آن پرداختیم. در این مقاله، شما را با مفهوم تنشهای اصلی و تنشهای برشی ماکسیمم آشنا خواهیم کرد. در انتها نیز به تشریح یک مثال خواهیم پرداخت.
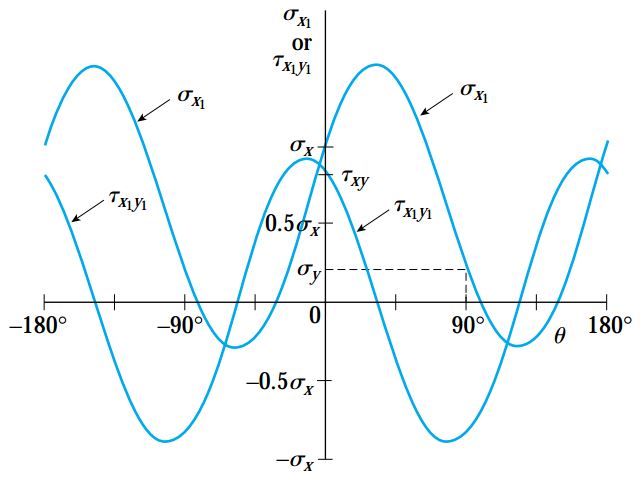
بر اساس معادلات تبدیل تنش صفحهای، دوران محورها تحت زاویه θ باعث تغییر پیوسته تنشهای نرمال σx1 و تنشهای برشی τx1y1 میشود. در شکل زیر، نمونهای از تغییر تنشهای نرمال و برشی با توجه به تغییر زاویه θ نمایش داده شده است. با توجه به این شکل، تنشهای نرمال و برشی در هر 90 درجه به میزان ماکسیمم و مینیمم خود میرسند.
مشخصاً این مقادیر ماکسیمم و مینیمم در حین فرآیندهای طراحی و تحلیل سازه مورد استفاده قرار میگیرند. به عنوان مثال، شکست ناشی از خستگی در سازهها معمولاً به دلیل اعمال تنشهای ماکسیمم رخ میدهد. به همین دلیل، تعیین مقدار و جهتگیری این تنشها به عنوان یکی از مهمترین مراحل طراحی سازه مد نظر قرار میگیرد.
تنشهای اصلی
تنشهای نرمال ماکسیمم و مینیمم با عنوان «تنشهای اصلی» (Principal Stresses) شناخته میشوند. مقادیر این تنشها با استفاده از معادله تبدیل زیر مورد محاسبه قرار میگیرند:
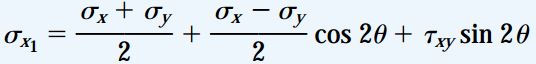
با مشتقگیری از σx1 نسبت به θ و برابر قرار دادن عبارت به دست آمده با صفر، معادله زیر حاصل میشود. با حل این معادله نسبت به θ، زوایایی به دست میآید که σx1 در آنها دارای مقادیر ماکسیمم و مینیمم است.
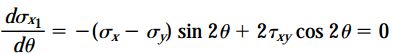
با استفاده از روابط مثلثاتی میتوانیم رابطه تعیین زوایای 2θp را به صورت زیر بیان کنیم:
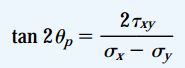
اندیس p در زاویه θp معرف جهتگیری صفحاتی است که تنشهای اصلی بر روی آنها قرار دارند و به آنها «صفحات اصلی» (Principal Planes) گفته میشود.
با استفاده از رابطه بالا و در محدوده 0 تا 360 درجه، دو مقدار برای زاویه 2θp به دست میآید که یکی از آنها در محدوده 0 تا 180 و دیگری در محدوده 180 تا 360 قرار دارد. اختلاف بین این مقادیر 180 درجه است. به این ترتیب، یکی از مقادیر θp در محدوده 0 تا 90 و دیگری در محدوده 90 تا 180 قرار خواهد داشت و اختلاف بین آنها 90 درجه خواهد بود. در یکی از این زوایا، تنش نرمال σx1 به عنوان «تنش اصلی ماکسیمم» (Maximum Principal Stress) و در زاویه دیگر، تنش نرمال σx1 به عنوان «تنش اصلی مینیمم» (Minimum Principal Stress) در نظر گرفته میشود.
با قرار دادن مقادیر θp در اولین معادله تبدیل و حل کردن معادله نسبت به σx1، تنشهای اصلی به دست میآیند. در این روش نه تنها مقادیر تنشهای اصلی بلکه زوایای مربوط به هر یک نیز مشخص میشوند. علاوه بر روش بالا میتوان از چند فرمول کلی نیز برای محاسبه تنشهای اصلی استفاده کرد. برای آشنایی با این روش، مثلث نمایش داده شده در شکل زیر را در نظر بگیرید. این مثلث بر اساس رابطه تعیین زوایای 2θp ترسیم شده است.
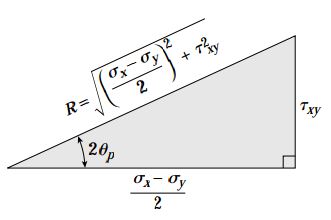
طبق نظریه فیثاغورس، طول وتر مثلث بالا برابر است با:
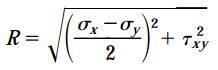
کمیت R در این رابطه دارای مقداری مثبت است. این کمیت با واحد تنش بیان میشود. بر اساس نظریه فیثاغورس میتوان به دو رابطه زیر نیز دست یافت:
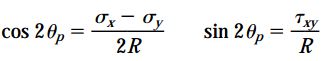
با بازنویسی رابطه σx1 بر اساس cos2θp و sin2θp، رابطه زیر برای تعیین تنش اصلی ماکسیمم (σ1) به دست میآید:
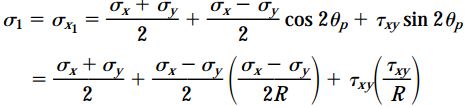
با جایگذاری رابطه کمیت R، معادله σ1 به فرم زیر تبدیل میشود:

به عنوان یک نکته مهم در نظر داشته باشید که جمع تنشهای نرمال موجود بر روی صفحات عمود بر هم مقداری ثابت است:

به این ترتیب، با جایگذاری رابطه σ1 در معادله بالا، رابطه تنش اصلی مینیمم (σ2) نیز به دست میآید:

فرم رابطه بالا مشابه رابطه σ1 است؛ با این تفاوت که به جای علامت مثبت بین دو عبارت سمت راست در رابطه σ1، یک علامت منفی بین دو عبارت سمت راست رابطه σ2 وجود دارد.
با ترکیب روابط معرفی شده برای σ1 و σ2، یک رابطه کلی برای تعیین تنشهای اصلی به دست میآید:
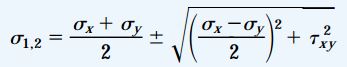
در این رابطه کلی، با به کارگیری علامت مثبت، تنش اصلی ماکسیمم (σ1) و با به کارگیری علامت منفی، تنش اصلی مینیمم (σ2) محاسبه میشود.
زوایای اصلی
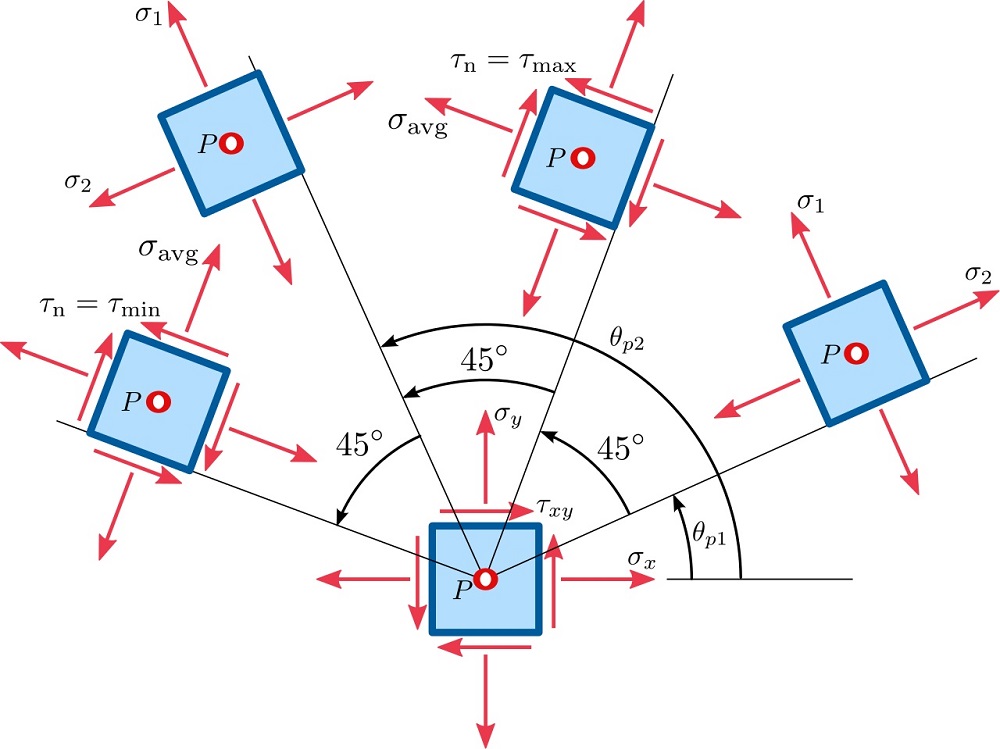
در این بخش به بررسی صفحات دربرگیرنده تنشهای اصلی و زوایای معرف آنها میپردازیم. مقادیر زوایای اصلی با استفاده از روابط tan2θp قابل محاسبه هستند. با این وجود، تفاوت بین θp1 و θp2 در این روابط مشخص نمیشود. یک روش ساده برای تعیین زاویه اصلی ماکسیمم یا مینیمم، جایگذاری مقدار یکی از زوایا در رابطه σx1 و مقایسه آن با تنشهای اصلی به دست آمده از رابطه کلی σ1,2 است. اگر مقدار σx1 با σ1 برابر باشد، زاویه به کار گرفته شده به عنوان زاویه اصلی ماکسیمم و اگر مقدار σx1 با σ2 برابر باشد، زاویه به کار گرفته شده به عنوان زاویه اصلی مینیمم در نظر گرفته خواهد شد.
یک روش دیگر برای تشخیص زوایای اصلی ماکسیمم و مینیمم، استفاده از روابط cos2θp و sin2θp است. توجه داشته باشید که تنها زاویه θp1 در روابط مذکور صدق میکند. به این ترتیب میتوانیم این روابط را به صورت زیر بازنویسی کنیم:
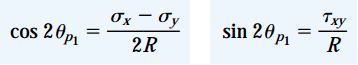
در محدوده 0 تا 360 درجه، تنها یک زاویه وجود دارد که میتواند به طور همزمان در هر دو رابطه بالا صدق کند. بنابراین، مقدار θp1 از طریق این روابط قابل محاسبه است. زاویه θp2، صفحه دربرگیرنده σ2 را نمایش میدهد. از آنجایی که صفحات دربرگیرنده تنشهای اصلی بر هم عمود هستند، مقدار θp2 به اندازه 90 درجه کوچکتر یا بزرگتر از زاویه θp1 خواهد بود.
مقدار تنشهای برشی بر روی صفحات اصلی
یکی از ویژگیهای مهم صفحات اصلی، امکان تعیین آنها با استفاده از معادلات تبدیل تنشهای برشی است. اگر تنش برشی τx1y1 را برابر با صفر قرار دهیم، معادله زیر به دست میآید:
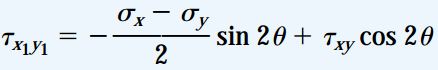
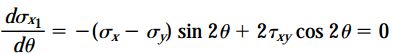
در صورت حل رابطه τx1y1 بر حسب tan2θ، به رابطه زیر میرسیم:
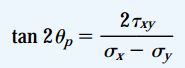
به عبارت دیگر، مقدار تنشهای برشی بر روی صفحات اصلی صفر است.
حالتهای خاص تنشهای اصلی
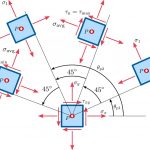
صفحات x و y در المانهایی که تحت تنش تکمحوری و دومحوری قرار دارند، به عنوان صفحات اصلی آنها در نظر گرفته میشوند (شکل زیر). مقدار tan2θp در این حالتهای خاص برابر با صفر و در نتیجه، زاویه θp دارای مقادیر 0 و 90 است. به علاوه، صفر بودن تنشهای برشی بر روی صفحات x و y، یکی دیگر از دلایل اصلی بودن این صفحات به شمار میرود.

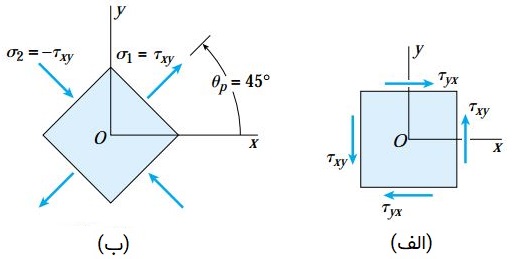
برای المانهایی که تحت برش خالص قرار دارند، صفحات اصلی نسبت به محور x به اندازه 45 درجه اختلاف زاویه دارند (شکل زیر). به دلیل بینهایت بودن مقدار tan2θp در این وضعیت، زاویه θp دارای مقادیر 45 و 135 خواهد بود. اگر τxy مثبت باشد، مقدار تنشهای اصلی σ1=τxy و σ2=-τxy است.
تنش اصلی سوم
در بخشهای قبلی، مبحث تنشهای اصلی و دوران محورها را تنها در صفحه xy (دوران حول محور z) مورد بررسی قرار دادیم. تنشهای اصلی محاسبه شده در این حالت با عنوان «تنشهای اصلی درونصفحهای» (In-Plane Principal Stresses) شناخته میشوند. با همه این تفاسیر نباید سهبعدی بودن المان تنش در مسائل واقعی را نادیده بگیریم. در واقع، هر المان تنش دارای سه تنش اصلی اعمال شونده بر روی سه صفحه متعامد است.
با اجرای یک تحلیل سهبعدی کاملتر میتوان مشاهده کرد که سه صفحه اصلی یک المان تنش از دو صفحه اصلی معرفی شده در بخشهای قبلی و صفحه z المان تشکیل میشوند. شکل زیر، سه صفحه اصلی یک المان تنش را نمایش میدهد. در شکل ب، المان تنش تحت زاویه اصلی θp1 دوران یافته است. مقادیر تنشهای اصلی σ1 و σ2 با استفاده از رابطه کلی σ1,2 تعیین میشوند؛ در صورتی که تنش اصلی سوم (σ3) برابر با صفر در نظر گرفته شده است.
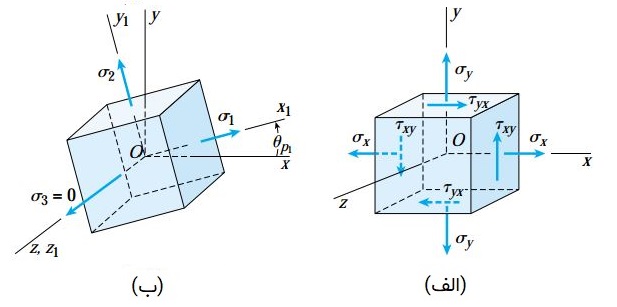
با توجه به تعاریف ارائه شده در بخشهای قبلی، مقدار σ1 بزرگتر از σ2 در نظر گرفته میشود. اگرچه، مقدار σ3 میتواند در محدودهای کوچکتر، بزرگتر یا بین σ1 و σ2 قرار داشته باشد. علاوه بر این، امکان برابر بودن یک، دو یا هر سه تنش اصلی نیز وجود دارد. به خاطر داشته باشید که هیچ تنش برشی بر روی هیچیک از صفحات اصلی رخ نمیدهد.
تنشهای برشی ماکسیمم
پس از تعیین مقدار و جهتگیری تنشهای اصلی، به محاسبه تنشهای برشی ماکسیمم و صفحات دربرگیرنده آنها میپردازیم. تنشهای برشی اعمال شده بر روی صفحات دوران یافته (τx1y1) با استفاده از معادلات تبدیل محاسبه میشوند.
با مشتقگیری از رابطه τx1y1 نسبت به پارامتر θ و برابر قرار دادن عبارت به دست آمده با صفر، به معادله زیر میرسیم:
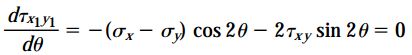
با اعمال تغییرات جزئی در رابطه بالا، خواهیم داشت:
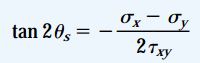
اندیس s در این رابطه نشان میدهد که زاویه θs، معرف جهتگیری تنشهای برشی ماکسیمم مثبت و منفی است. با حل رابطه بالا، یک زاویه بین 0 تا 90 درجه و زاویهای دیگر بین 90 تا 180 درجه به دست میآید. در تنشهای برشی ماکسیمم نیز مانند تنشهای اصلی، مقادیر به دست آمده برای جهتگیری صفحات دربرگیرنده تنش (در اینجا θs) به اندازه 90 درجه با یکدیگر اختلاف دارند.
بنابراین، تنشهای برشی ماکسیمم نیز بر روی صفحات عمود بر هم رخ میدهند. با توجه به مطالب ارائه شده در مبحث «تنش و کرنش برشی»، میدانیم که مقادیر قدر مطلق تنشهای برشی موجود بر روی صفحات عمود، با هم برابر هستند. به همین دلیل، تنشهای برشی ماکسیمم منفی و مثبت تنها در علامت با یکدیگر اختلاف دارند. با مقایسه روابط θs و θp داریم:
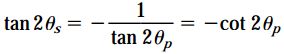
بنابراین میتوان رابطهای را بین θs و θp ایجاد کرد. به این منظور، ابتدا رابطه بالا را به صورت زیر بازنویسی میکنیم:
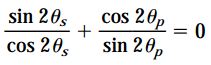
با ضرب جداگانه هر یک از مخرجها در عبارت بالا، به رابطه زیر میرسیم:
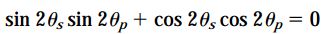
با توجه به روابط مثلثاتی، معادله بالا به عبارت زیر تبدیل میشود:
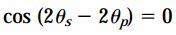
بنابراین:
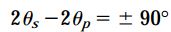
و
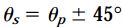
معادله بالا نشان میدهد که صفحات تنش برشی ماکسیمم نسبت به صفحات اصلی، به اندازه 45 درجه اختلاف زاویه قرار دارند. صفحه تنش برشی ماکسیمم مثبت (τmax) با زاویه θs1 مشخص میشود. برای تعیین زاویه θs1 میتوان از روابط زیر استفاده کرد:
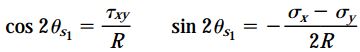
پارامتر R در رابطه بالا به صورت زیر محاسبه میشود:
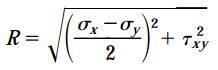
رابطه بین زاویه θs1 و زاویه θp1 نیز به صورت زیر خواهد بود:
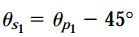
با جایگذاری روابط cosθs1 و sinθs1 در معادلات تبدیل، به رابطه زیر دست مییابیم:
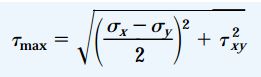
تنش برشی ماکسیمم منفی (τmin) دارای مقدار برابر با τmax و علامت مخالف آن است.
رابطه تنش برشی ماکسیمم را میتوان بر حسب پارامترهای σ1 و σ2 نیز بیان کرد. این رابطه به صورت زیر نوشته میشود:
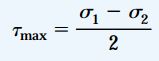
بنابراین، تنش برشی ماکسیمم با نصف اختلاف بین تنشهای اصلی برابر است. توجه داشته باشید که تنشهای نرمال بر روی صفحات تنشهای برشی ماکسیمم وجود دارند. با جایگذاری رابطه زاویه θs1 در رابطه تنش σx1، مقدار تنش نرمال اعمال شده بر روی صفحات تنش برشی ماکسیمم مثبت به دست میآید. تنش به دست آمده با میانگین تنشهای نرمال بر روی صفحات x و y برابر خواهد بود:
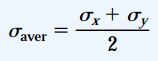
این تنش نرمال بر روی صفحات تنش برشی ماکسیمم منفی نیز اعمال میشود. در حالتهای خاص نظیر تنش تکمحوری و دومحوری، صفحات تنش برشی ماکسیمم در موقعیت 45 درجه نسبت به محورهای x و y قرار دارند. در حالت برش خالص، تنشهای برشی ماکسیمم بر روی صفحات x و y رخ میدهند.
تنشهای برشی درونصفحهای و خارجصفحهای
در بخش قبلی به تحلیل تنشهای برشی درونصفحهای پرداختیم. این تنشها تنها بر روی صفحه xy اعمال میشوند. به منظور تعیین تنشهای برشی ماکسیمم درونصفحهای، المانهای حاصل از دوران دستگاه مختصات xyz تحت محور z را در نظر گرفتیم (شکل زیر). به علاوه، مشاهده کردیم که تنشهای برشی ماکسیمم بر روی صفحاتی با اختلاف 45 درجه نسبت به صفحات اصلی قرار دارند. در صفحات اصلی المان زیر، تنشهای اصلی با σ1 و σ2 نمایش داده شدهاند. بنابراین، تنشهای برشی ماکسیممِ درونصفحهای، از دوران 45 درجهای دستگاه مختصات x1y1z1 نسبت محور z1 به دست میآیند. روابط مورد نیاز برای محاسبه این تنشها در بخش قبلی ارائه شدند.

با دوران 45 درجهایِ دستگاه مختصات نسبت به محورهای x1 و y1 نیز میتوان تنشهای برشی ماکسیمم را تعیین کرد. به این ترتیب، سه دسته تنش برشی ماکسیمم مثبت و منفی به دست میآید:
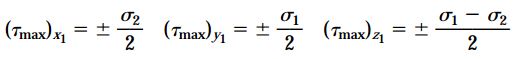
اندیسهای تنشهای برشی (y1 ،x1 یا z1)، محوری را نمایش میدهند که دستگاه مختصات نسبت به آن دوران یافته است. به تنشهای حاصل از دوران حول محورهای x1 و y1، «تنشهای برشی خارجصفحهای» (Out-of-Plane Shear Stresses) گفته میشود. با توجه به مقادیر جبری σ1 و σ2 میتوان بزرگی تنشهای برشی ماکسیمم را نسبت به یکدیگر مشخص کرد. در صورت هم علامت σ1 و σ2، مقدار عددی τmax)x1) یا τmax)y1) بزرگتر از دیگر موارد خواهد بود. در صورت مختلف العلامت بودن σ1 و σ2، مقدار عددی τmax)z1) بزرگتر از دیگر موارد خواهد بود.
مثال
المانی مطابق شکل زیر در معرض تنش صفحهای قرار دارد. با توجه به اطلاعات نمایش داده شده در شکل موارد الف و ب را تعیین کنید:
- الف) تنشهای اصلی و جهتگیری آنها
- ب) تنشهای برشی ماکسیمم و جهتگیری آنها

σx=12300psi, σy=-4200psi, τxy=-4700psi
الف) تنشهای اصلی
برای تعیین مقادیر تنشهای اصلی دو روش وجود دارد.
روش اول
زوایای دربرگیرنده صفحات اصلی (θp) به صورت زیر تعیین میشوند:
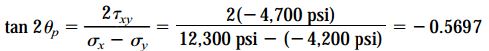
با حل رابطه بالا نسبت به زاویه θp، به دو مقدار زیر دست مییابیم:

و
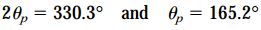
با جایگذاری مقادیر بالا در معادلات تبدیل، امکان محاسبه تنشهای اصلی فراهم میشود. پیش از انجام این محاسبات، مقادیر مربوط به عبارتهای زیر را تعیین میکنیم:

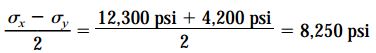
با جایگذاری مقدار اول 2θp در معادله σx1، داریم:
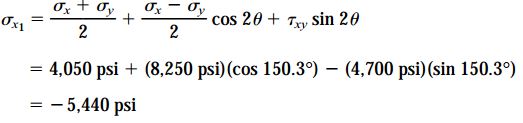
به همین ترتیب، با جایگذاری مقدار دوم 2θp به σx1=13540psi دست مییابیم. در نتیجه، تنشهای اصلی و زوایای مربوط به هریک از آنها به صورت زیر خواهند بود:

توجه داشته باشید که دو زاویه اصلی، 90 درجه با یکدیگر اختلاف دارند و رابطه σ1+σ2=σx+σy بین تنشهای نرمال برقرار است.
روش دوم
در این روش میتوان مقادیر تنشهای اصلی را از طریق رابطه کلی σ1,2 محاسبه کرد:

به این ترتیب:
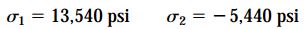
زاویه صفحهای که تنش اصلی σ1 بر روی آن اعمال میشود (θp1) نیز با استفاده از روابط زیر به دست میآید:
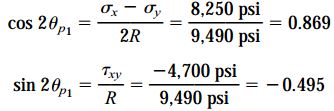
تنها زاویهای که سینوس و کسینوس آن در رابطه بالا صدق میکند، 2θp1=330.3 است. به این ترتیب، زاویه صفحهای که تنش اصلی ماکسیمم (σx1=13540psi) در آن رخ میدهد، θp1=165.2 درجه خواهد بود. زاویه اصلی دیگر به اندازه 90 درجه با زاویه اول اختلاف دارد. در نتیجه، زاویه صفحهای که تنش اصلی مینیمم (σx2=5440psi) در آن رخ میدهد، θp2=75.2 درجه است. توجه داشته باشید که تنشهای اصلی و زوایای اصلی به دست آمده در این روش با مقادیر به دست آمده از روش قبلی یکسان هستند.
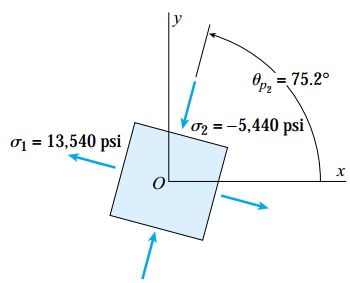
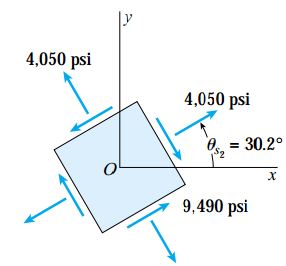
ب) تنشهای برشی ماکسیمم
تنش برشی ماکسیممِ درونصفحهای به صورت زیر محاسبه میشود:

برای تعیین زاویه θs1 از رابطه زیر استفاده میکنیم:
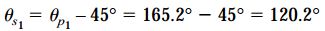
زاویه صفحهای که تنش برشی ماکسیمم منفی در آن اعمال میشود نیز به صورت زیر تعیین میشود:

تنشهای نرمال اعمال شده بر روی صفحات دربرگیرنده تنشهای برشی ماکسیمم نیز برابرند با:
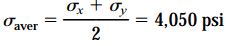
^^













سپاس از زحمات شما
بسیار کمکم کردید.
سلام، رفرنس این مطلب رو لطفا ارسال کنید، متشکرم
سلام، وقت شما بخیر؛
منابع کلیه مطالب مجله فرادرس در صورتیکه ترجمه یا تالیف باشند، حتماً در انتهای آنها و پس از بخش معرفی مطالب و دورههای آموزشی ذکر شدهاند.
از اینکه با مجله فرادرس همراه هستید بسیار سپاسگزاریم.
سلام … عالی است … در انتخاب اساتید دقت فراوان لازم است … سواد تنها کافی نیست … قدرت بیان و کلام هم به تنهائی جواب کار را نمی دهد. هیچگاه مطالب علمی را فدای زمان نمی شود کرد…بعضی از درسهای شما را خریداری کرده ام … یکی دو جلسل اول خوب توضیح می دهند و خوب تشریح می کنند … ام جلسلت پایانی با سرعت از روی نوشته می خوانند و سر وته مطلب را به هم می آورند… در مجموع کارتا بی نظیر است … تا زمانی که نظیری برایش نیامده باشد… سعی کنید بی نظیر بمانید…از مجرب ها استفاده کنید… ممنون.