آموزش هندسه مسطحه — به زبان ساده

هندسه مسطحه، ترجمه زبان ناشناخته سطوح است؛ زبانی که به کمک آن انسان توانست دری به‌سوی علم بگشاید. اگر دوست داشته باشید که چیزی بکشید، هندسه مسطحه در خدمت شما خواهد بود.
هندسه مسطحه در مورد شکل‌های مسطح یا کاملا صاف مانند خط‌‌، دایره، مثلث و سایر شکل‌هایی‌ است که می‌توان آن‌ها را روی سطح‌های صاف کشید. این سطح می‌تواند تخته‌سیاه کلاس باشد یا کاغذی سفید و صاف که تا بی‌نهایت ادامه دارد.

نقطه، خط، سطح و حجم در هندسه مسطحه

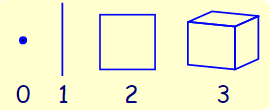
قبل از پرداختن به موضوع بالا لازم است تعریفی از مفهوم بُعد (Dimension) داشته باشیم. در هندسه می‌توان ابعاد مختلفی داشت؛ تعداد بُعدها در یک شکل به این معنی است که چند مقدار برای توصیف محل نقاط در شکل مورد‌نظر نیاز است.

نقطه: در دنیای صفربعدی قرار گرفته است، اندازه ندارد و فقط یک مفهوم است.
خط: اگر یک نقطه را وادار کنیم به یک جهت حرکت کند، خط به وجود می‌آید. به عبارت دیگر هر خط از تعداد بی‌شماری نقطه پی‌درپی ساخته می‌شود. خط تنها یک بعد دارد که همان طول خط است. خط هیچ انتهایی ندارد.
سطح: همانطور که حرکت نقطه در فضا خط ایجاد می‌کند، حرکت پاره‌خط در فضا یا روی صفحه در یک جهت معین، موجب پدید آمدن سطح می‌شود. سطح شکلی است که دو بعدِ طول و عرض دارد.
حجم: با حرکت یک سطح مشخص در فضا، حجم به‌وجود می‌آید؛ به‌عنوان‌مثال با حرکت یک سطح مربع شکل، مکعب و با حرکت یک سطح دایره شکل، کره به وجود می‌آید. حجم دارای سه بعدِ طول، عرض و ارتفاع(عمق) است، ازاین‌رو آن را سه بعدی (3D) می‌نامند. جهانی که ما در آن زندگی می‌کنیم سه‌بعدی است.

شکل‌های دوبعدی در هندسه مسطحه

شکل‌های دوبعدی شامل مثلث، چهارضلعی، چندضلعی‌های منتظم و نامنتظم، شکل‌های محدب و مقعر، دایره، بیضی و ... می‌شوند.

مثلث

مثلث یک چندضلعی است که تنها از سه ضلع تشکیل شده است و سه زاویه دارد. جمع هر سه زاویه در یک مثلث همیشه برابر 180 درجه است.

انواع مثلث در زیر آمده است.

مثلث متساوی‌الاضلاع: مثلثی است که دارای سه ضلع با طول مساوی است، علاوه‌براین زاویه‌های داخلی این مثلث با هم برابر هستند.
مثلث متساوی‌الساقین: مثلثی است که دارای دو ضلع با طول مساوی است و دو زاویه داخلی برابر دارد.
مثلث قائم‌الزاویه: مثلثی است که یکی از زاویه‌های آن برابر 90 درجه است. نسبت‌های مثلثاتی مانند sin و cos بر روی این مثلث تعریف می‌شوند.
مثلث منفرجه: مثلثی است که یکی از زاویه‌های داخلی آن بیشتر از 90 درجه است.
مثلث حاده: مثلثی است که تمام زاویه‌های داخلی آن کمتر از 90 درجه باشد.

چهارضلعی‌ها

چهارضلعی‌های هندسی شامل موارد زیر می‌شوند.

مستطیل: در هندسه به شکلی مستطیل گفته می‌شود که دارای چهار ضلع باشد، ضلع‌های روبه‌رو باهم مساوی و موازی باشند و با یکدیگر به‌صورت دوبه‌دو، زاویه‌ 90 درجه بسازند.
لوزی: یک چهارضلعی است که ضلع‌هایش باهم برابر هستند. در لوزی قطر‌ها برهم عمودند.
مربع: مربع شکلی مسطح است که چهار ضلع آن باهم برابر و مساوی هستند و هر چهار زاویه آن 90 درجه است. ضلع‌های روبه‌رو در یک مربع باهم موازی‌اند.
متوازی‌الاضلاع: یک چهارضلعی است که ضلع‌های روبه‌رو در آن با‌هم موازی و مساوی هستند. زاویه‌های روبه‌رو در این شکل با‌هم برابر هستند. این در حالی است که زاویه‌های مجاور در متوازی‌الاضلاع مکمل هم هستند، یعنی جمع هر دو زاویه‌ی کنار هم برابر با 180 درجه است.
ذوزنقه: شکلی است چهارضلعی که فقط دو ضلع آن با‌هم موازی هستند. در این شکل، زاویه‌های مجاور به دو ضلع غیر موازی، مکمل هم هستند.
کایت (Kite): کایت یا شبه‌لوزی، یک چهارضلعی است که دارای دو جفت ضلع مجاور با دو اندازه مختلف باشد. یک کایت دارای دو قطر عمود برهم است. به این نوع چهارضلعی، لوزی بادبادکی هم می‌گویند چون بهترین شکل هندسی برای ساخت یک بادبادک است.

برای مطالعه بیشتر در مورد چهارضلعی‌ها به مطلب «چهار ضلعی ها — به زبان ساده» در وبلاگ فرادرس مراجعه کنید.

چندضلعی‌ها (بیش از چهار ضلع)

یک چندضلعی، شکلی دوبعدی است که از خطوط راست تشکیل شده است.

• چندضلعی‌های منتظم: هنگامی‌که تمام زاویه‌ها و تمام ضلع‌ها در یک شکل دو بعدی با‌هم برابر باشند، شکل منتظم است، در غیر این صورت شکل نامتعارف یا نامنتظم خواهد بود.
• چندضلعی مقعر: هنگامی‌که یکی زاویه‌های داخلی یک شکل دوبعدی بزرگ‌تر از 180 درجه باشد، شکل چندضلعی مقعر است.
• چندضلعی محدب: هنگامی‌که تمام زاویه‌های داخلی یک شکل دوبعدی کوچک‌تر از 180 درجه باشد، شکل چندضلعی محدب است.
• چندضلعی محاطی: اگر یک چندضلعی به‌گونه‌ای درون یک دایره قرار بگیرد که تمام راس‌های آن روی دایره باشند، این چندضلعی محاطی نام دارد.
• چندضلعی محیطی: اگر دایره‌ای درون یک چندضلعی به‌گونه‌ای قرار بگیرد که تمام ضلع‌ها در نقطه وسطشان با آن دایره مماس باشند، آن چندضلعی محیطی نام دارد.

نکته: به‌جز مثلث و چندضلعی‌های منتظم، بقیه‌‌ی چندضلعی‌ها این خصوصیت را ندارند.

دایره

دایره مکان هندسی نقاطی از صفحه است که فاصله‌شان از نقطه ثابتی واقع در آن صفحه، مقداری ثابت است.

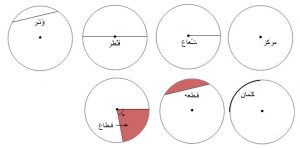
مرکز دایره: نقطه‌ای است که دقیق در وسط دایره قرار دارد.شعاع دایره: خطی است که از مرکز به پیرامون دایره کشیده می‌شود، شعاع را با حرف r نشان می‌دهیم. شعاع نیمی از قطر است.
قطر دایره: خطی روی دایره است که از مرکز می‌گذرد. قطر دایره را با حرف d نشان می‌دهیم.
وتر دایره: خطی است که به دو نقطه روی پیرامون دایره وصل می‌شود، وتر از مرکز دایره عبور نمی‌کند.
کمان دایره: تکه‌ای از پیرامون دایره است.
قطعه‌ی دایره: سطحی در دایره است که با کمان و یک وتر محدود باشد.
قطاع دایره: سطحی در دایره است که با یک کمان و دو وتر مربوط به کمان، محدود باشد.

مخروط‌ها و بیضی‌ها

مجموعه‌ی نقطه‌ها یعنی گردآمدن چیزی از یک نوع؛ به‌عنوان‌مثال مجموعه نقطه‌ها روی یک سطح که بافاصله یکسان از یک نقطه مرکزی قرارگرفته باشند، یک دایره را می‌سازند. در هندسه به مجموعه نقاطی که یک نوع خاصیت دارند، مکان هندسی گفته می‌شود. یک بیضی، مکان هندسی نقاطی است که مجموع فاصله‌شان از دو نقطه ثابت به یک اندازه باشد.
می‌توان از روش‌های دیگری نیز به دایره و بیضی رسید و آن برش زدن یک مخروط است.

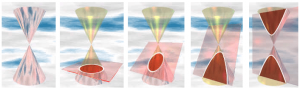
در حقیقت یک مخروط دارای چند مکان هندسی است. به‌عنوان‌مثال مقطع یا سطح پایه مخروط به شکل دایره، برش عرضی آن به شکل مثلث، برش اریب یا مایل آن بیضی شکل و هرچه زاویه برش بیشتر باشد، شکل به دست آمده، از یک بیضی به منحنی تبدیل می‌شود.

می‌توان خیلی ساده و با استفاده از دو پونز و یک تکه نخ، دایره و بیضی را رسم کرد. درواقع ابزارها‌ی رسم در هندسه بسیار ساده هستند، این ابزارها شامل پرگار، خط کش و مداد می‌شوند.

مروری کوتاه بر چند مفهوم پایه‌ای در هندسه مسطحه

موزاییک‌های هندسی

زمانی که یک سطح به‌گونه‌ای با یک الگو از اشکال هندسی پوشانده شود که بین آن‌ها هیچ همپوشانی یا شکافی وجود نداشته باشد، سطح به وجود آمده یک موزاییک هندسی نامیده می‌شود.

مختصات هندسی

دستگاه مختصات از دو محور عمود بر هم ساخته شده است. محور افقی، محور طول یا محور X است و محور عمودی، محور عرض یا محور Y نام دارد. محل برخورد این دو محور، مبدا مختصات است که آن را با صفر نشان می‌دهند.

فیثاغورس (Pythagoras)

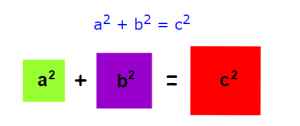
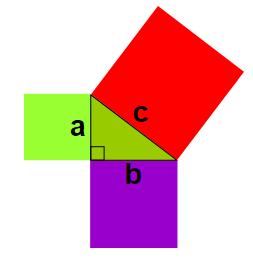
بیش از دو هزار سال پیش، ریاضی‌دانی به نام فیثاغورث به کشف شگفت‌انگیزی در مورد مثلث‌ها رسید؛ هنگامی‌که یک مثلث قائم‌الزاویه (90 درجه) وجود داشته باشد و روی هر یک از سه ضلع آن، یک مربع تشکیل شود، آنگاه بزرگ‌ترین مربع مساحتی برابر با مساحت مجموع دو مربع دیگر دارد. این کشف به‌عنوان قضیه فیثاغورث مشهور شد.

سمبل‌های هندسی

سمبل‌های خاص زیادی در هندسه مسطحه وجود دارند. استفاده از آن‌ها باعث صرفه‌جویی در زمان و فضا هنگام نوشتن روی کاغذ می‌شود. به‌عنوان‌مثال برای نمایش دو خط موازی در هندسه مسطحه از سمبل «||» استفاده می‌شود.

متجانس و مشابه

تجانس در هندسه مسطحه به معنی «تبدیل» به‌صورتی است که شکل‌ها را در تمام جهت‌ها، با یک مقیاس، بزرگ یا کوچک می‌کند. هنگامی دو شکل مشابه هستند که تمام اجزای آن‌ها جزبه‌جز باهم مساوی باشند.

زاویه در هندسه مسطحه

زاویه‌ها را با توجه به اندازه‌شان به صورت زیر طبقه‌بندی می‌کنند.

• زاویه تند: زاویه را تند یا حاده می‌گویند هرگاه اندازه‌اش کمتر از 90 درجه باشد.
• زاویه راست: زاویه را راست یا قائم می‌گویند هرگاه اندازه آن برابر 90 درجه باشد.
• زاویه باز: زاویه را باز یا منفرجه می‌گویند هرگاه بزرگ‌تر از 90 درجه و کمتر از 180 درجه باشد.
• زاویه نیم صفحه: زاویه‌ای را نیم صفحه می‌گوییم هرگاه برابر 180 درجه باشد.
• زاویه بازتاب: زاویه‌ای را بازتاب می‌گوییم هرگاه بزرگ‌تر از 180 درجه و کمتر از 360 درجه باشد.
• زاویه کامل: زاویه‌ای را کامل یا تمام صفحه می‌گوییم هرگاه برابر 360 درجه باشد.
• زاویه خارجی: یک زاویه بین یک ضلع از شکل و خطی است که از ضلع مجاور امتداد پیدا کرده است. زاویه‌ی خارجی با زاویه‌ی داخلی کنارش مکمل هم هستند یعنی با‌هم زاویه 180 درجه را تشکیل می‌دهند.
• زاویه داخلی: زاویه بین دو ضلع که داخل یک چندضلعی قرار می‌گیرد، زاویه داخلی نام دارد.

هندسه مسطحه، سخت یا آسان؟

هندسه‌ انتهایی ندارد. ما در این پست روزنه‌ای شاید به اندازه یک سر سوزن را باز کردیم و نگاهی گذرا به آن انداختیم. چه قبول داشته باشیم و چه نه، این جهان و تمام شگفتی‌های درون آن بر پایه علم ریاضی است.

شاید عده‌ای از ما دل خوشی از هندسه نداریم اما باور کنید این هندسه نیست که سخت است. بلکه این نوع نگاه و نوع تدریس است که سخت یا آسان بودن چیزی را تعیین می‌کند. برای عده‌ای فتح یک قله چند هزار متری خواب‌و‌خیالی بیش نیست اما برای کسانی که عاشقانه به انتظار لحظه‌ای هستند که طلوع خورشید را صد هزار متر بالاتر از بقیه انسان‌ها به تماشا بنشینند، فتح قله‌ای به آن عظمت، تنها یک مسیر برای رسیدن به آن لحظه است. مسیری که با برداشتن گام‌هایی آرام اما پیوسته و استوار طی می‌شود.

نوع نگاه انسان‌ها، نوع زندگی آن‌ها را در این جهان پر از شگفتی تعیین می‌کند.

اگر تمایل به مطالعه بیشتر در مورد این موضوعات را داشته باشید؛ شاید آموزش های زیر نیز برای شما مفید باشند:

• آشنایی با تبدیلات هندسی — به زبان ساده
• حرکت انتقالی در ریاضیات — به زبان ساده
• آشنایی با چند وجهی ها — به زبان ساده
• چهار ضلعی ها — به زبان ساده

#

منبع