متغیر تصادفی و توزیع چند جمله ای (Multinomial Distribution) — به زبان ساده

در نوشته‌های دیگر فرادرس با «توزیع دو جمله‌ای» (Binomial Distribution) آشنا شدید. همانجا اشاره کردیم که متغیر تصادفی دو جمله‌ای از حاصل جمع n متغیر تصادفی برنولی مستقل و هم توزیع با احتمال موفقیت یکسان بدست می‌آید. متغیر «تصادفی چند جمله‌ای» (Multinomial Random Variable) نیز حالت کلی‌تری برای متغیر تصادفی دو جمله‌ای و توزیع آن نیز به همین ترتیب حالت کلی‌تری از توزیع دو جمله‌ای است. در این نوشتار به بررسی توزیع چند جمله‌ای و خصوصیات آن می‌پردازیم. برای آگاهی بیشتر درباره متغیر تصادفی و تابع احتمال و توزیع احتمال به مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال مراجعه کنید. همچنین خواندن نوشتار اصول شمارش و فاکتوریل — به زبان ساده نیز خالی از لطف نیست.

متغیر تصادفی و توزیع چند جمله ای (Multinomial Distribution)

در نظریه آمار و احتمال، حالت کلی‌تر برای توزیع دوجمله‌ای، «توزیع چند جمله‌ای» (Multinomial Distribution) نام دارد. برای مثال اگر تعداد اعداد مشاهده شده در n بار پرتاب تاس را در نظر بگیریم، می‌توان آن را یک توزیع چند جمله‌ای در نظر گرفت. در این حالت نتایج آزمایش، دو حالتی نیستند.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

در این حالت می‌توان کل تعداد حالات برای نتایج یکبار انجام آزمایش تصادفی مستقل را k در نظر گرفت. فرض کنید چنین آزمایشی n بار تکرار شده است. احتمال موفقیت برای هر بار اجرای آزمایش را می‌توان به صورت $$p_1, p_2, \cdots, p_k$$ در نظر گرفت. همچنین تعداد موفقیت را به صورت $$x_1, x_2, \cdots, x_n$$ در نظر می‌گیریم که در آن $$x_i\in \{0,1,2,\cdots,n\}$$‌ است. پس به نظر می‌رسد که $$i=1,2,\cdots,k$$ بوده و به علت مستقل بودن هر یک از آزمایش‌ها داریم:

$$\large P(X_1=x_1,X_2=x_2,\cdots,X_k=x_k)=\dfrac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}\\ \large \sum x_i=n,\; \sum p_i=1,\; i=1,2,\cdots,k$$

مشخص است که این متغیر تصادفی kبعدی و دارای تکیه‌گاه اعداد طبیعی است. بنابراین از دسته توزیع‌های گسسته محسوب می‌شود. با توجه به رابطه بالا می‌توان تابع احتمال (pdf) یا (Probability Density Function) و تابع «توزیع احتمال تجمعی» (cdf) یا (Cumulative Distribution Function) را نوشت.

تابع احتمال و تابع توزیع احتمال

فرض کنید در یک آزمایش شرکت کرده‌ایم که در آن باید n توپ از k رنگ مختلف را با جایگذاری انجام دهیم. توپ‌های هم رنگ یکسان در نظر گرفته می‌شوند. متغیر تصادفی $$X_i$$ را تعداد توپ‌های استخراج شده از رنگ i در نظر گرفته‌ایم. همچنین $$p_i$$ نیز احتمال آن را نشان می‌دهد که توپ انتخابی از رنگ i باشد. در این صورت تابع احتمال متغیر تصادفی X به صورت زیر نوشته خواهد شد.

$$\large f(x_1,x_2,\cdots x_k)=P(X_1=x_1,X_2=x_2,\cdots,X_k=x_k)=\\ \large \dfrac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k},\;\;\;\sum x_i=n,\;\;\; \sum p_i=1 $$

در این حالت می‌نویسیم $$X=(X_1,x_2,\cdots,X_k)\sim MN(n,p_1, p_2,\cdots, p_k)$$ است و می‌خوانیم X دارای توزیع چند جمله‌ای با پارامترهای n و $$p_1,p_2,\cdots,p_k$$ است.

نکته: هر یک از $$X_i$$ در این حالت دارای توزیع دو جمله‌ای با پارامترهای n و $$p_i$$ هستند. در نتیجه می‌توان گفت $$X_i\sim Binom(n,p_i)$$.

همینطور تابع احتمال این متغیر تصادفی را می‌توان برحسب تابع گاما نیز به صورت زیر نوشت:

$$\large f(x_1,\dots, x_{k}; p_1,\ldots, p_k) = \frac{\Gamma(\sum_i x_i + 1)}{\prod_i \Gamma(x_i+1)} \prod_{i=1}^k p_i^{x_i}$$

همچنین برای تابع توزیع احتمال تجمعی نیز خواهیم داشت:

$$\large F(x)=P(X_1\leq x_1,X_2\leq x_2,\cdots,X_k\leq x_k)$$

نکته: از آنجایی بسط چند جمله‌ای $$(p_{1}x_{1}+p_{2}x_{2}+p_{3}x_{3}+\cdots +p_{k}x_{k})^{n}$$ ضرایب توزیع چند جمله‌ای را می‌سازد، این توزیع به نام چند جمله‌ای معروف است.

خصوصیات توزیع چند جمله‌ای

مشخص است که هر کدام از $$X_i$$ دارای توزیع دو جمله‌ای هستند. در نتیجه امید ریاضی به صورت برداری از $$E(X_i)=np_i$$ ها ساخته می‌شود.

همینطور برای محاسبه واریانس $$X_i$$ و کوواریانس متغیر $$X_i,X_j$$ داریم:

$$\large Var(X_i)=np_i(1-p_i)$$

$$\large Cov(X_i,X_j)=-np_ip_j ,\;\;(i\neq j)$$

نکته: همانطور که دیده می‌شود کوواریانس متغیر تصادفی چند جمله‌ای منفی است که البته منطقی به نظر می‌رسد زیرا با افزایش مقدار مثلا $$x_i$$ باید $$x_j$$ کاهش یابد زیرا مجموع همه آن‌ها برابر با n است.

همچنین براساس محاسبات می‌توان نشان داد که ضریب همبستگی بین $$X_i$$ و $$X_j$$ منفی است و به صورت زیر قابل محاسبه است:

$$\large \rho(X_i,X_j)=\dfrac{cov(X_i,X_j)}{\sqrt{Var(X_i)Var(X_j)}}=-\sqrt{\dfrac{p_ip_j}{(1-p_i)(1-p_j)}}$$

جالب است که پارامتر n در مقدار ضریب همبستگی نقشی ندارد.

مثال

فرض کنید در یک انتخابات، سه کاندید با اسامی A, B, C شرکت کرده‌اند. احتمال موفقیت کاندید A برابر با ۲۰٪ و کاندید B برابر با ۳۰٪ و کاندید C نیز برابر با ۵۰٪ است. اگر شش رای‌دهنده به تصادف انتخاب شوند، احتمال اینکه دقیقا یک نفر به کاندید A، دو نفر به B و سه نفر به C رای دهند، به صورتی که در ادامه آمده است محاسبه می‌شود.

در اینجا فرض بر این است که اندازه جامعه بزرگ است و انتخاب این ۶ نفر تغییری در احتمال انتخاب شدن هر یک از کاندیدها ندارد. به این ترتیب خواهیم داشت:

$$\large P(A=1,B=2,C=3)=\dfrac{6!}{1!2!3!}(0.2)^1(0.3)^2(0.5)^3=0.135$$

توزیع‌های مرتبط با توزیع چند جمله‌ای

با توجه به حالت کلی که توزیع چند جمله‌ای نسبت به توزیع دو جمله‌ای دارد، می‌توان گفت:

• به ازای k=2 توزیع متغیر تصادفی X به دو جمله‌ای تبدیل خواهد شد.
• اگر n=1 و k=2 باشد، توزیع برنولی و در حالتی که n=1 و k>2 باشد «توزیع طبقه‌ای» (Categorical Distribution) نامیده می‌شود.

نکته: اگر در نتایج یک آزمایش گسسته بیش از ۲ حالت در نظر گرفته شود، تابع توزیع احتمال آن را با نام طبقه‌ای می‌شناسند. در این حالت، نتیجه آزمایش یکی از k‌ حالت مختلف خواهد بود که احتمال رخداد آن نیز به صورت $$p_k$$‌ نوشته می‌شود.

شبیه‌سازی توزیع چند جمله‌ای

روش‌های مختلفی برای ایجاد داده‌های شبیه‌سازی شده از توزیع چند جمله‌ای وجود دارد. در اینجا به بررسی یک روش ساده به کمک اکسل می‌پردازیم.

فیلم آموزش متغیرهای تصادفی (الف) در آمار و احتمال مهندسی (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

کافی است که یک عدد تصادفی تولید کنید و به کمک روابطی که در جدول‌های زیر می‌بینید، بردار تصادفی مورد نظر را ایجاد کنید.

مثال

فرض کنید که جدول از طبقات و احتمالات مربوط به هر طبقه در اختیارمان قرار گرفته است.

نکته: کران بالا برای احتمال رده، همان احتمالات تجمعی رده‌ها است.

حال به کمک رابطه‌های زیر، داده‌هایی (بردار) از توزیع چند جمله‌ای را ایجاد می‌کنیم.

حال این فرمول‌ها را در اکسل وارد می‌کنیم. مشخص است که مقدار سلول Ai با استفاده از تابع Rand یک عدد تصادفی است.

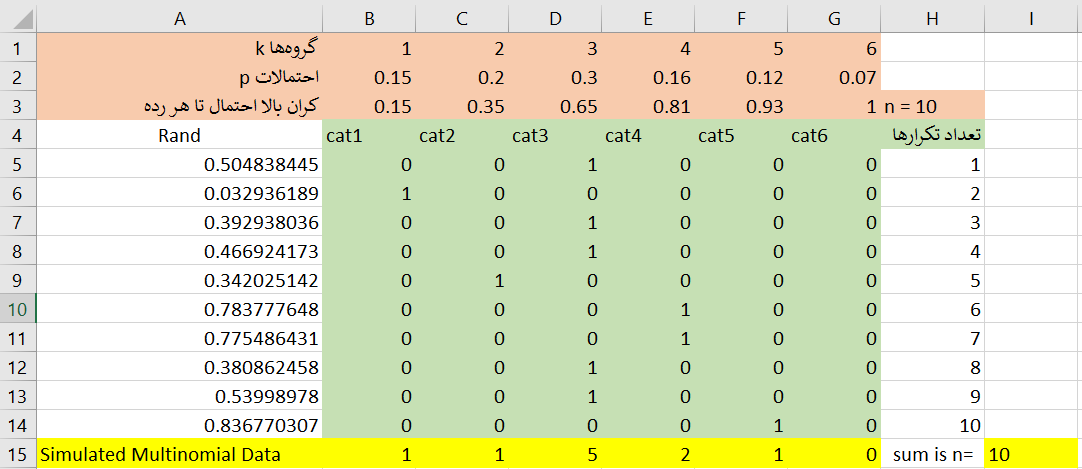
همانطور که مشخص است این آزمایش ۱۰ بار از سطر ۵ تا ۱۴ تکرار و در هر بار یک عدد تصادفی متعلق به یک بازه ایجاد شده است. مجموع مشاهدات حاصل از این ۱۰ بار تکرار، اعداد تصادفی مربوط به توزیع چند جمله‌ای با پارامترهای n=10 و $$p_1=0.15,\;\; p_2=0.2,\;\; p_3=0.3,\;\; p_4=0.16,\;\; p_5=0.12,\;\; p_6=0.07$$ را ایجاد می‌کند. همانطور که انتظار داشتیم، گروه یا دسته‌ای که شانس بیشتری برای مشاهده داشت (یعنی گروه ۳) تعداد بیشتری دارد. فایل مربوط به این محاسبات را می‌توانید از اینجا دریافت کنید.

نکته: اگر فایل اکسل را دریافت و مشاهده کنید، ممکن است نتایج با تصویر این مطلب متفاوت باشد زیرا با هر بار تغییر یا بازکردن فایل اکسل، اعداد تصادفی جدید تولید شده و در نتیجه شبیه‌سازی توزیع چند جمله‌ای نتایج متفاوتی خواهد داشت.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساد
• آموزش قضیه بسط دو جمله ای و مثلث خیام

^^