رسم دایره مور برای حالت تنش صفحه ای — آموزش جامع

در مبحث تنش صفحه‌ای، به معرفی این نوع تنش و معادلات تبدیل مرتبط با آن پرداختیم. رسم «دایره مور» (Mohr’s Circle)، یک روش ساده برای نمایش گرافیکی معادلات تبدیل تنش صفحه‌ای است. این نمایش گرافیکی، امکان درک روابط بین تنش‌های نرمال و برشی اعمال شده بر روی صفحات دوران‌یافته در یک نقطه خاص از ماده را فراهم می‌کند. دایره مور به منظور محاسبه تنش‌های اصلی، تنش‌های برشی ماکسیمم و تنش‌های موجود بر روی صفحات دوران‌یافته نیز مورد استفاده قرار می‌گیرد. این دایره برای کمیت‌های مشابه تنش مانند کرنش و ممان اینرسی نیز به کار می‌رود. در این مقاله، کاربرد دایره مور دایره در محاسبه مؤلفه‌های تنش صفحه‌ای را مورد ارزیابی قرار می‌دهیم. در انتها نیز به منظور آشنایی بیشتر شما با نحوه استفاده از این ابزار گرافیکی در مسائل مهندسی، به تشریح چند مثال کاربردی می‌پردازیم.

معادلات دایره مور

معادلات مربوط به دایره مور را می‌توان از طریق معادلات تبدیل تنش صفحه‌ای به دست آورد. در بخش زیر، معادلات تبدیل تنش صفحه‌ای را به همراه یک تغییر جزئی در معادله اول مشاهده می‌کنید:

 

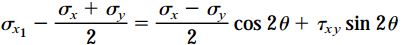
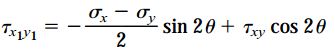
با اجرای تحلیل‌های هندسی متوجه خواهید شد که این دو معادله مشابه معادله دایره هستند. زاویه 2θ به عنوان پارامتر و تنش‌های σ_x1 و τ_x1y1 به عنوان مختصات دایره در نظر گرفته می‌شوند.

درک ماهیت این معادلات و شباهت آن‌ها به معادله دایره برای انجام تحلیل‌های تنش-کرنش بسیار ضروری است. به این منظور، در ابتدا پارامتر 2θ را از معادلات بالا حذف می‌کنیم. این کار با به توان 2 رساندن طرفین معادلات و جمع آن‌ها با یکدیگر انجام می‌شود. به این ترتیب داریم:

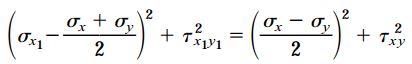
با استفاده از روابط زیر می‌توان معادله بالا را به فرم ساده‌تری تبدیل کرد:

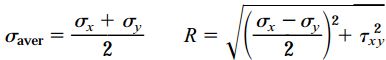
به این ترتیب:

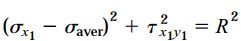
این رابطه، فرم استاندارد معادله یک دایره را نمایش می‌دهد. مختصات نقاط روی این دایره با مقادیر (σ_x1,τ_x1y1)، شعاع دایره با مقدار R و مرکز آن با مختصات (σ_aver,τ_x1y1) نمایش داده می‌شوند.

حالت‌های رسم دایره مور

با استفاده از معادلات ارائه شده در بخش قبلی می‌توان دایره مور را به دو حالت مختلف رسم کرد.

در حالت اول، مقادیر مثبت تنش نرمال σ_x1 در سمت راست و مقادیر مثبت تنش برشی τ_x1y1 در قسمت پایینی محورهای مختصات دایره مور رسم می‌شوند (شکل زیر).

مزیت استفاده از این روش، مثبت بودن زاویه 2θ در جهت پادساعتگرد و مطابقت آن با راستای مثبت 2θ در معادلات تبدیل به دست آمده از شکل‌های زیر است.

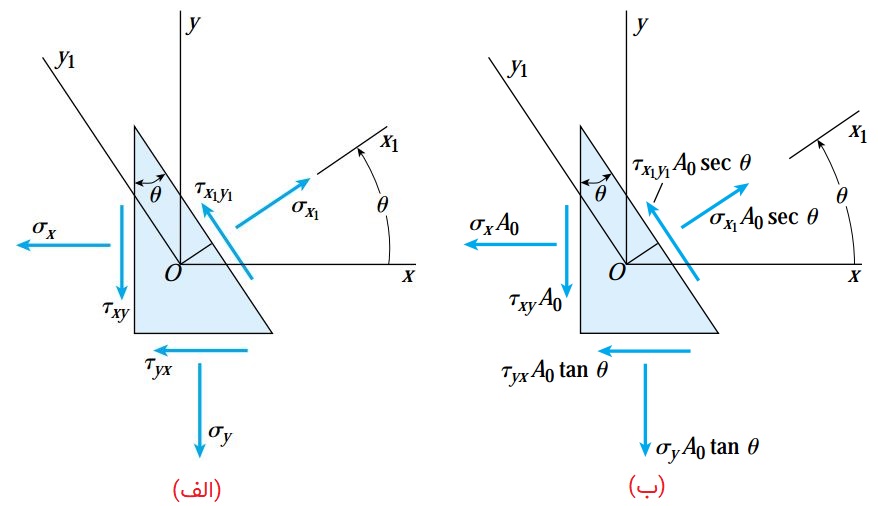
در حالت دوم، مقادیر مثبت تنش برشی τ_x1y1 در قسمت بالایی محورهای مختصات دایره مور رسم می‌شوند و زاویه 2θ در جهت ساعتگرد مثبت است (شکل زیر).

هر دو روش بالا از نظر مبانی ریاضی صحیح هستند و استفاده از هیچ‌کدام از آن‌ها مانعی ندارد. با این وجود، اگر جهت مثبت زاویه 2θ و جهت مثبت المان با هم مطابقت داشته باشند، به تصویر کشیدن جهت‌گیری مؤلفه‌های تنش آسان‌تر خواهد بود. علاوه بر این، چرخش پادساعتگرد با قاعده دست راست نیز مطابقت دارد. به همین دلیل، در این مقاله از روش اول رسم دایره استفاده خواهیم کرد.

مراحل رسم دایره مور

دایره مور را می‌توان با استفاده از روش‌های مختلفی رسم کرد. انتخاب هر یک از این روش‌ها به معلوم یا مجهول بودن مولفه‌های تنش بستگی دارد.

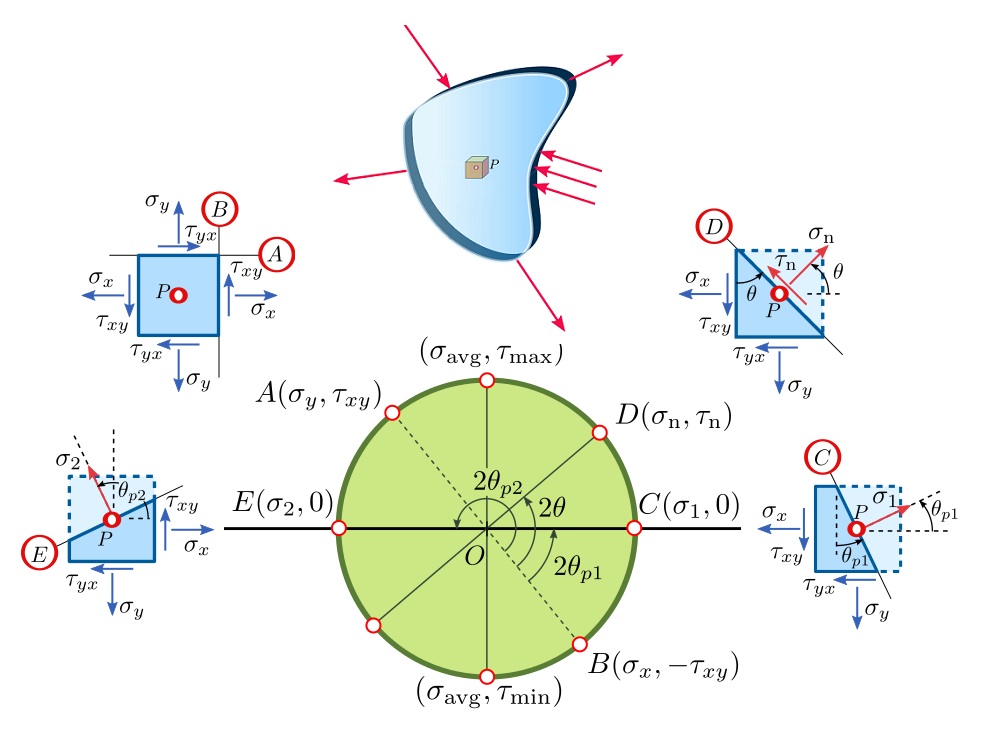
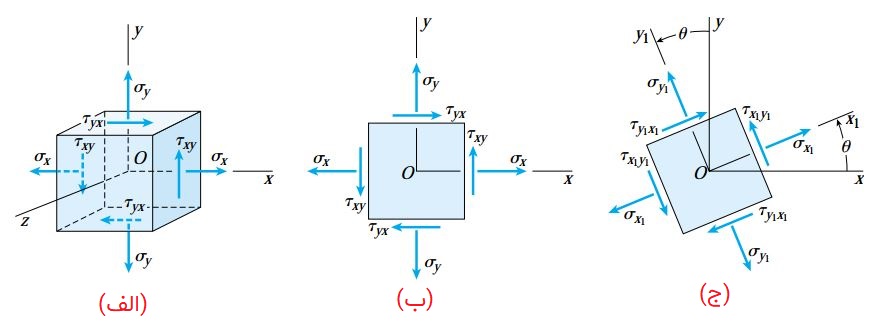
به منظور نمایش ویژگی‌های اصلی دایره مور، فرض می‌کنیم که مقادیر تنش‌های σ_y ، σ_x و τ_xy بر روی صفحات x و y در یک المان تنش صفحه‌ای مشخص هستند (شکل زیر).

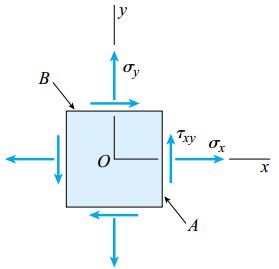
مشخص بودن این مقادیر برای رسم دایره مور کفایت می‌کند. با رسم دایره می‌توانیم مقادیر تنش‌های σ_y1 ، σ_x1 و τ_x1y1 بر روی یک المان دوران‌یافته مانند شکل زیر را محاسبه کنیم. علاوه بر این، تنش‌های اصلی و تنش‌های برشی ماکسیمم نیز قابل تعیین خواهند بود.

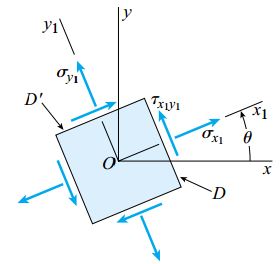
دایره مور نمایش داده شده در شکل زیر را در نظر بگیرید.

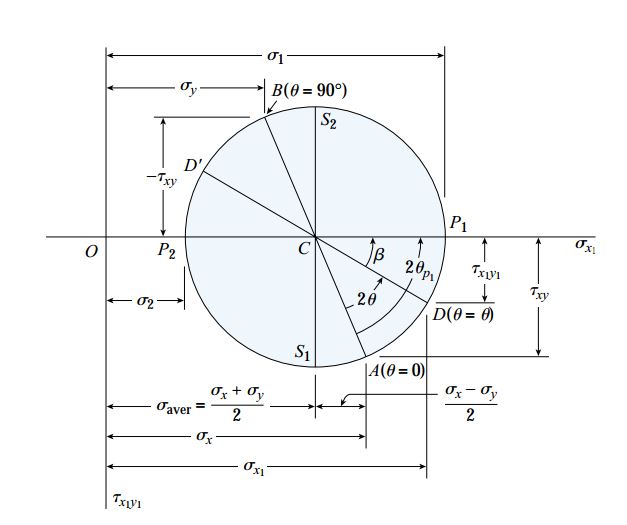
به منظور رسم این دایره باید مراحل زیر را انجام دهید:

• در ابتدا یک دستگاه محورهای مختصات با محور افقی σ_x1 (مقادیر مثبت در سمت راست) و محور عمودی τ_x1y1 (مقادیر مثبت در بخش پایین) را رسم کنید.
• محل قرارگیری مرکز دایره (نقطه C) را در مختصات σ_x1=σ_aver و τ_x1y1=0 مشخص کنید.
• محل قرارگیری نقطه A (معرف شرایط تنش بر روی صفحه x المان) را در مختصات σ_x1=σ_x و τ_x1y1=τ_xy مشخص کنید. توجه داشته باشید که زاویه مربوط به نقطه A بر روی دایره مور برابر با θ=0 در نظر گرفته می‌شود.
• محل قرارگیری نقطه B (معرف شرایط تنش بر روی صفحه y المان) را در مختصات σ_x1=σ_y و τ_x1y1=τ_xy مشخص کنید. توجه داشته باشید که زاویه مربوط به نقطه B بر روی دایره مور برابر با θ=90 در نظر گرفته می‌شود. نقاط معرف A و B بر روی المان تنش در شکل زیر نمایش داده شده‌اند.

• یک خط راست از نقطه A تا B رسم کنید. این خط همان قطر دایره است که از مرکز C عبور می‌کند. نقاط A و B، تنش‌های موجود بر روی صفحاتی با اختلاف 90 درجه را نمایش می‌دهند (شکل بالا). این نقاط بر روی دو انتهای قطر دایره قرار دارند. از این‌رو، اختلاف زاویه آن‌ها بر روی دایره 180 درجه است.
• با انتخاب نقطه C به عنوان مرکز، دایره مور را به گونه‌ای رسم می‌کنیم که از روی نقاط A و B عبور کند. شعاع دایره رسم شده با این روش R خواهد بود.

پس از رسم دایره و استفاده از روابط هندسی می‌توان نشان داد که خطوط CA و CB، شعاع‌های دایره هستند و طول آن‌ها برابر با R است. طول مختصات نقاط C و A به ترتیب با مقادیر σ_x+σ_y)/2) و σ_x برابری می‌کند. از این‌رو، اختلاف بین طول این نقاط بر روی محور افقی برابر با σ_x-σ_y)/2) خواهد بود (شکل بالا). به علاوه، نقطه A ارتفاعی برابر با τ_xy دارد. به این ترتیب، خط CA را می‌توان به عنوان وتر یک مثلث در نظر گرفت که طول یکی از اضلاع آن σ_x-σ_y)/2) و طول ضلع دیگر آن τ_xy است. با گرفتن جذر از مجموع مربعات این دو ضلع، رابطه شعاع دایره مور (R) به فرم زیر درمی‌آید:

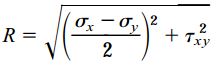
رابطه بالا مشابه رابطه معرفی شده در بخش معادلات دایره مور است. با یک روش مشابه می‌توانیم ثابت کنیم که طول خط CB با شعاع دایره (R) برابری می‌کند.

تنش‌های موجود بر روی یک المان دوران یافته

اکنون تنش‌های اعمال شده بر روی صفحات المان دوران یافته تحت زاویه θ نسبت به محور x یعنی تنش‌های σ_y1 ،σ_x1 و τ_x1y1 را در نظر می‌گیریم. اگر زاویه θ مشخص باشد، تنش‌های مذکور با استفاده از دایره مور قابل تعیین خواهند بود.

به این منظور، ابتدا به اندازه 2θ از شعاع CA در جهت پادساعتگرد حرکت می‌کنیم و نقطه D با مختصات σ_x1 و τ_x1y1 را بر روی دایره علامت می‌زنیم. نقطه D، تنش‌های موجود بر روی صفحه x₁ در المان نمایش داده شده در شکل بالا را نمایش می‌دهد.

توجه داشته باشید که زاویه 2θ بر روی دایره مور با زاویه θ بر روی المان تنش برابر است. به عنوان مثال، نقطه D بر روی دایره مور به اندازه 2θ با نقطه A اختلاف دارد اما اختلاف زاویه صفحه x₁ با صفحه x بر روی المان به اندازه θ است (شکل بالا و پایین را با هم مقایسه کنید).

به منظور نمایش تطابق بین مختصات نقطه D بر روی دایره مور (σ_x1,τ_x1y1) و معادلات تبدیل تنش صفحه‌ای از هندسه دایره کمک می‌گیریم. به این منظور، ابتدا زاویه بین خط CD و محور σ_x1 با حرف β نمایش می‌دهیم. سپس، با توجه به هندسه دایره روابط زیر را برای تعیین مختصات نقطه D به دست می‌آوریم:

توجه داشته باشید که زاویه بین شعاع CA و محور افقی مختصات برابر با 2θ+β است. بنابراین:

با بسط سینوس و کسینوس به روابط زیر می‌رسیم:

با ضرب cos2θ در رابطه اول، ضرب sin2θ در رابطه دوم و جمع این دو رابطه با هم خواهیم داشت:

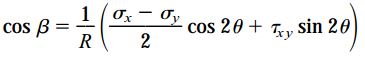
با ضرب sin2θ در رابطه اول، ضرب cos2θ در رابطه دوم و تفریق این دو رابطه از هم نیز خواهیم داشت:

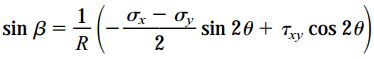
اگر روابط cosβ و sinβ را در روابط اول و دوم جایگذاری کنیم، به معادلات تبدیل σ_x1 و τ_x1y1 می‌رسیم. بنابراین، نقطه D با زاویه 2θ بر روی دایره مور، وضعیت تنش بر روی صفحه x₁ با زاویه θ بر روی المان را نمایش می‌دهد.

نقطه 'D در مقابل نقطه D قرار دارد. اختلاف زاویه بین نقاط 180 درجه است. بنابراین، نقطه 'D بر روی دایره، تنش‌های موجود بر روی صفحه‌ای با اختلاف 90 نسبت به نقطه D بر روی المان تنش را نمایش می‌دهد. به این ترتیب، مختصات نقطه 'D بر روی دایره مور، بیانگر مقادیر تنش‌های σ_y1 و τ_x1y1 بر روی صفحه y در المان تنش است (شکل‌های بالا و پایین را با هم مقایسه کنید).

در این بخش، به معرفی نحوه نمایش مؤلفه‌های تنش بر روی نقاط دایره مور و ارتباط آن‌ها با تنش‌های اعمال شده بر روی یک المان پرداختیم. تنش‌های موجود بر روی یک المان دوران یافته تحت زاویه θ توسط مختصات نقطه‌ای با اختلاف زاویه 2θ نسبت به نقطه مرجع (A) بر روی دایره مور مشخص می‌شوند.

بنابراین، با دوران محورهای x₁y₁ تحت زاویه θ در جهت پادساعتگرد، نقطه مربوط به صفحه x₁ به اندازه 2θ در جهت پادساعتگرد بر روی دایره مور حرکت می‌کند. به همین ترتیب، در صورت دوران محورهای مختصات به اندازه یک زاویه مشخص در جهت ساعتگرد، نقطه مورد بررسی بر روی دایره مور به اندازه دو برابر آن زاویه در جهت ساعتگرد حرکت خواهد کرد.

تنش‌های اصلی

تعیین تنش‌های اصلی به عنوان مهم‌ترین کاربرد دایره مور محسوب می‌شود. توجه داشته باشید که در نقطه P₁ بر روی دایره مور، تنش نرمال به بیشترین مقدار خود و تنش برشی به کمترین مقدار خود (صفر) می‌رسد. از این‌رو، نقطه P₁ یکی از تنش‌های اصلی و یکی از صفحات اصلی را نمایش می‌دهد.

طول نقطه P₁، به عنوان مقدار تنش اصلی بزرگ (σ₁) و زاویه آن نسبت به نقطه مرجع (2θ_p1)، به عنوان جهت‌گیری صفحه اصلی در نظر گرفته می‌شود. صفحه اصلی مربوط به تنش اصلی کوچک نیز با نقطه P₂ و در مقابل نقطه P₁ بر روی دایره مشخص می‌شود.

بر اساس هندسه دایره مور، تنش اصلی بزرگ برابر است با:

با جایگذاری رابطه R در رابطه بالا، معادله زیر به دست می‌آید:

به همین ترتیب می‌توان مطابقت بین معادله σ₂ با روابط هندسی موجود بر روی دایره مور را تأیید کرد. زاویه اصلی بین محور x و صفحه تنش اصلی بزرگ در المان تنش (θ_p1)، نصفِ زاویه بین خطوط CA و CP₁ بر روی دایره مور (2θ_p1) است. با بررسی دایره می‌توان روابط زیر را بین کسینوس و سینوس زاویه 2θ_p1 با پارامترهای تنش مشاهده کرد:

این روابط با روابط به دست آمده از معادلات تعادل تنش صفحه‌ای یکسان هستند. بنابراین، روابط هندسی به دست آمده از دایره مور در این مورد نیز با معادلات تعادل مطابقت دارند. توجه داشته باشید که اختلاف بین زاویه اصلی 2θ_p2 با 2θ_p1 بر روی دایره مور 180 درجه است. بنابراین، رابطه θ_p2=θ_p1+90 در اینجا نیز برقرار خواهد بود.

تنش‌های برشی ماکسیمم

نقاط S₁ و S₂ بر روی دایره موهر، صفحات دربرگیرنده تنش‌های برشی ماکسیمم مثبت و منفی را نمایش می‌دهند. همان‌گونه در شکل زیر مشاهده می‌کنید، این S₁ و S₂ بر روی بالاترین و پایین‌ترین نقاط دایره قرار دارند.

اختلاف زاویه بین محل قرارگیری این نقاط با نقاط P₁  و P₂ به اندازه 2θ=90 است. این موضوع، اختلاف 45 درجه‌ای صفحات دربرگیرنده تنش‌های برشی ماکسیمم نسبت به صفحات اصلی را تأیید می‌کند.

مقدار عددی تنش‌های برشی ماکسیمم با شعاع دایره مور برابر است. به علاوه، تنش‌های نرمال موجود بر روی صفحات دربرگیرنده تنش‌های برشی ماکسیمم با طول نقطه C بر روی محور افقی دستگاه مختصات، یعنی تنش نرمال میانگین (σ_aver) برابری می‌کند.

قاعده علامت‌گذاری تنش‌های برشی

در برخی مواقع از یک قاعده علامت‌گذاری متفاوت برای نمایش تنش‌های برشی بر روی دایره مور استفاده قرار می‌گیرد. در این قاعده، جهت‌گیری یک تنش برشی اعمال شده بر روی المان توسط تعیین جهت دوران آن مشخص می‌شود (شکل زیر).

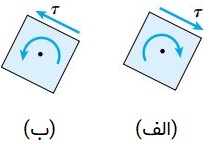
در صورتی که تنش برشی τ باعث چرخش ساعتگرد المان تنش شود، به آن «تنش برشی ساعتگرد» (Clockwise Shear Stress) و اگر تنش برشی منجر به چرخش پادساعتگرد المان تنش شود، به آن «تنش برشی پادساعتگرد» (Counterclockwise Shear Stress) گفته می‌شود. در هنگام رسم دایره مور، تنش‌های برشی ساعتگرد در بخش بالایی و تنش‌های برشی پادساعتگرد در بخش پایینی محورهای مختصات قرار می‌گیرند.

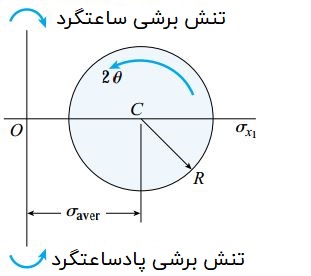
به عنوان یک نکته مهم به خاطر داشته باشید که دایره به دست آمده در این روش با دایره مورد بررسی در بخش‌های قبلی یکسان است؛ چراکه تنش برشی مثبت به عنوان یک تنش برشی پادساعتگرد (در بخش بالایی محورهای مختصات) و تنش برشی منفی به عنوان یک تنش برشی ساعتگرد (در بخش پایینی محورهای مختصات) در نظر گرفته می‌شود.

استفاده از این روش جایگزین صرفاً یک نقطه نظر متفاوت از نحوه عملکرد مؤلفه‌های تنش برشی بر روی محورهای مختصات دایره مور را فراهم می‌کند. در این نقطه نظر متفاوت، به جای در نظر گرفتن بخش بالایی محور عمودی به عنوان محل قرارگیری تنش‌های برشی منفی و بخش پایینی آن به عنوان محل قرارگیری تنش‌های برشی مثبت، بخش بالایی محور عمودی به عنوان محل قرارگیری تنش‌های برشی ساعتگرد و بخش پایینی آن به عنوان محل قرارگیری تنش‌های برشی پادساعتگرد در نظر گرفته می‌شود. این رویکرد ملموس‌تر از رویکرد قبلی است.

نکات تکمیلی راجع به دایره مور

• در بخش‌های قبلی مشاهده کردیم که با استفاده از دایره می‌توان مقادیر تنش‌های اعمال شده بر روی یک صفحه دوران یافته، تنش‌های اصلی و تنش‌های برشی ماکسیمم را مور محاسبه کرد. در این مقاله، تنها دوران اعمال شده در صفحه xy را مد نظر قرار دادیم. بنابراین، تمام مؤلفه‌های موجود بر روی دایره مور، تنش‌های درون صفحه‌ای بودند.
• به منظور راحتی کار، دایره مور با فرض مثبت بودن تنش‌های σ_y ،σ_x و τ_xy رسم شد. با این وجود در صورت منفی بودن یک یا چند تنش نیز از یک فرآیند یکسان برای رسم دایره استفاده می‌شود. اگر یکی از تنش‌های نرمال منفی باشد، یک بخش یا تمام دایره بر روی بخش سمت چپ مبدأ مختصات قرار می‌گیرد.

• در شکل بالا، نقطه A تنش‌های موجود بر روی صفحه‌ای با زاویه θ=0 را نمایش می‌دهد. این نقطه می‌تواند در هر محلی از دایره قرار داشته باشد. به این ترتیب، بدون در نظر گرفتن محل قرارگیری نقطه A، زاویه 2θ همیشه به صورت پادساعتگرد اندازه‌گیری می‌شود.
• رسم دایره مور در حالت‌های خاص نظیر تنش تک‌محوری، تنش دومحوری و برش خالص ساده‌تر از رسم این دایره در حالت کلی تنش صفحه‌ای است.
• علاوه بر استفاده از دایره مور برای تعیین تنش‌های موجود بر روی صفحات دوران یافته در هنگام مشخص بودن تنش‌های موجود بر روی صفحات x و y، امکان بهره‌گیری از این به صورت معکوس نیز وجود دارد. به این ترتیب، در صورت مشخص بودن تنش‌های σ_y1 ،σ_x1 و τ_x1y1 بر روی یک المان دوران یافته تحت زاویه θ می‌توان با رسم یک دایره مور، مقادیر تنش‌های σ_y1 ،σ_x1 و τ_x1y1 برای زاویه θ=0 را به راحتی محاسبه کرد. به ابن منظور، ابتدا محل قرارگیری نقاط D و 'D بر روی دستگاه مختصات را با استفاده از تنش‌های معلوم مشخص کرده و با به کارگیری خط D'D به عنوان قطر، دایره مور را به مرکزیت این خط (نقطه C) رسم می‌کنیم. با حرکت منفی بر روی دایره به اندازه 2θ نسبت شعاع CD، محل قرارگیری نقطه A مشخص می‌شود. این نقطه، شرایط تنش بر روی صفحه x المان را نمایش می‌دهد. با رسم قطر دایره از نقطه A، موقعیت نقطه B نیز مشخص خواهد شد. در نهایت می‌توانیم با تعیین مختصات نقاط A و B، تنش‌های اعمال شده بر روی المان در زاویه θ=0 را محاسبه کنیم.
• رسم دایره مور با مقیاس برابر، امکان اندازه‌گیری مستقیم مقادیر تنش از روی مختصات دایره را فراهم می‌کند. با این وجود، استفاده از محاسبات عددی (معادلات تبدیل یا روابط مثلثاتی و هندسه دایره) به روش‌های دیگر ترجیح داده می‌شود.
• دایره مور امکان تصور رابطه بین تنش‌های اعمال شده بر روی صفحات المان در زوایای مختلف را فراهم می‌کند. به این علاوه، این دایره به عنوان یک دستگاه ذخیره‌سازی ساده برای انجام محاسبات تنش در نظر گرفته می‌شود. با وجود منسوخ شدن استفاده از روش‌های گرافیکی مختلف، سادگی و قابل فهم بودن دایره مور باعث تداوم آن به عنوان یک ابزار ارزشمند در مسائل مهندسی شده است.
• معادلات تبدیل کرنش صفحه‌ای و ممان اینرسی نواحی مسطح با معادلات تبدیل تنش صفحه‌ای مشابه هستند. از این‌رو، دایره مور برای تبدیل پارامترهای این موارد نیز کاربرد دارد.

مثال‌های کاربردی

در این بخش، به منظور آشنایی بیشتر با کاربرد دایره مور و نحوه استفاده از آن برای تعیین تنش‌های مختلف به تشریح کامل سه مثال کاربردی می‌پردازیم. در مثال اول، حالت تنش ساده دومحوری را بررسی می‌کنیم. در مثال دوم، تنش‌های برشی را نیز در نظر می‌گیریم. در مثال سوم، یک المان را با فرض وجود تنش‌های منفی مورد تحلیل قرار می‌دهیم.

مثال 1

نقطه‌ای بر روی سطح یک استوانه تحت فشار را در نظر بگیرید که در معرض تنش‌های دومحوری σ_x=90MPa و σ_y=20MPa قرار گرفته است. شکل زیر، المان مرتبط با نقطه مورد بررسی را نمایش می‌دهد.

با استفاده از دایره مور، مقادیر تنش‌های اعمال شده بر روی المان دوران یافته تحت زاویه θ=30 را تعیین کنید. (تنها حالت تنش صفحه‌ای را در نظر بگیرید و در انتها، نتایج به دست آمده را بر روی شکل المان دوران یافته نمایش دهید.)

رسم دایره مور

برای شروع کار، محورهای مختصات مربوط به تنش‌های نرمال و برشی را به گونه‌ای رسم می‌کنیم که مقادیر مثبت σ_x1 در سمت راست و مقادیر مثبت τ_x1y1 در بخش پایینی دستگاه مختصات قرار داشته باشند. شکل زیر، دایره نهایی مربوط به این مسئله را نمایش می‌دهد. در ادامه، با انجام محاسبات مورد نیاز به مقادیر نمایش داد شده بر روی این دایره خواهیم رسید.

در مرحله بعد، با محاسبه تنش نرمال میانگین σ_aver، محل قرارگیری مرکز دایره بر روی محور σ_x1 را مشخص می‌کنیم:

نقطه A، تنش‌های موجود بر روی صفحه x المان در زاویه θ=0 را نمایش می‌دهد. مختصات این نقطه برابر است با:

نقطه B، تنش‌های موجود بر روی صفحه y در زاویه θ=90 را نمایش می‌دهد. مختصات این نقطه نیز برابر است با:

اکنون می‌توانیم دایره گذرنده از نقاط A و B را به مرکزیت C رسم کنیم. شعاع دایره را برابر با R در نظر می‌گیریم:

تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=30

مقادیر تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=30 توسط مختصات نقطه D بر روی دایره مشخص می‌شوند. این نقطه به اندازه 2θ=60 با نقطه A اختلاف زاویه دارد. با بررسی دایره مور مشاهده می‌شود که مختصات نقطه D به صورت زیر است:

به همین ترتیب، مختصات نقطه 'D در زاویه 2θ=240 تعیین می‌شود:

شکل زیر، نتایج به دست آمده برای المان دوران یافته تحت زاویه θ=30 را نمایش می‌دهد. توجه داشته باشید که جمع تنش‌های نرمال بر روی المان دوران یافته (σ_x1+σ_y1) با جمع تنش‌های نرمال بر روی المان اولیه (σ_x+σ_y) برابر است.

مثال 2

یک المان کوچک بر روی یک دستگاه بزرگ را در نظر بگیرید که تحت تنش صفحه‌ای با مقادیر σ_y=5000psi ،σ_x=15000psi و τ_xy=400psi قرار دارد (شکل زیر).

با استفاده از دایره مور، مقادیر مربوط به کمیت‌های زیر را تعیین کنید:

• الف) تنش‌های اعمال شده بر روی المان دوران یافته تحت زاویه θ=40
• ب) تنش‌های اصلی
• ج) تنش‌های برشی ماکسیمم

رسم دایره مور

برای رسم دایره مور مانند مثال قبل عمل می‌کنیم. به این ترتیب، مقادیر مثبت σ_x1 در سمت راست و مقادیر مثبت τ_x1y1 در بخش پایینی دستگاه مختصات قرار می‌گیرند. شکل زیر، دایره نهایی مربوط به این مسئله را نمایش می‌دهد. در ادامه، با انجام محاسبات مورد نیاز به مقادیر نمایش داد شده بر روی این دایره خواهیم رسید.

محل قرارگیری مرکز دایره بر روی محور σ_x1 با محاسبه تنش نرمال میانگین σ_aver مشخص می‌شود:

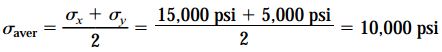
نقطه A، تنش‌های موجود بر روی صفحه x المان در زاویه θ=0 را نمایش می‌دهد. مختصات این نقطه برابر است با:

نقطه B، تنش‌های موجود بر روی صفحه y در زاویه θ=90 را نمایش می‌دهد. مختصات این نقطه نیز برابر است با:

اکنون می‌توانیم دایره گذرنده از نقاط A و B را به مرکزیت C رسم کنیم. شعاع دایره را برابر با R در نظر می‌گیریم:

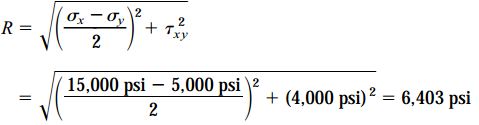
تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=40

مقادیر تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=40 با مشخص کردن مختصات نقطه D بر روی دایره تعیین می‌شوند. این نقطه به اندازه 2θ=80 با نقطه A اختلاف زاویه دارد. به منظور ارزیابی مختصات این نقطه باید زاویه بین خط CD با محور σ_x1 (زاویه DCP₁) و همچنین زاویه بین خط CA با محور σ_x1 (زاویه ACP₁) را تعیین کنیم. با توجه به هندسه دایره داریم:

با داشتن مقادیر این زوایا، مختصات نقطه D در زاویه 2θ=80 بر روی دایره به صورت زیر مشخص می‌شود:

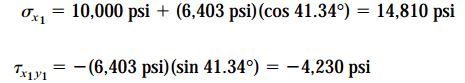
به همین ترتیب، مختصات نقطه 'D در زاویه در زاویه 2θ=260 نیز به صورت زیر تعیین خواهد شد:

شکل زیر، تنش‌های موجود بر روی المان دوران یافته تحت زاویه در زاویه θ=40 را نمایش می‌دهد. همان طور که مشاهده می‌شود، قاعده ثابت بودن جمع تنش‌های نرمال برای این مثال نیز صادق است.

تنش‌های اصلی

تنش‌های اصلی بر روی دایره مور با نقاط P₁ و P₂ نمایش داده می‌شوند.

بنابراین، تنش اصلی بزرگ برابر است با:

زاویه 2θ_p1 از نقطه A تا نقطه P₁ با زاویه ACP₁ بر روی دایره برابر است:

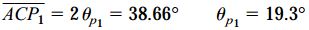
به این ترتیب، صفحه دربرگیرنده تنش اصلی بزرگ در المان تنش به اندازه θ_p1=19.3 نسبت به محور x دوران یافته است.

مختصات تنش اصلی کوچک (P₂) بر روی دایره نیز مشابه تنش اصلی بزرگ محاسبه می‌شود:

زاویه 2θ_p2 از نقطه A تا نقطه P₂ بر روی دایره با 38.66+180=218.66 برابر است. بنابراین، صفحه اصلی دوم در المان تنش به اندازه θ_p2=109.3 با محور x اختلاف زاویه دارد. شکل زیر، وضعیت تنش‌های اصلی بر روی المان تنش را نمایش می‌دهد.

تنش‌های برشی ماکسیمم

تنش‌های برشی ماکسیمم بر روی دایره مور با نقاط S₁ و S₂ نمایش داده می‌شوند. بنابراین، مقدار تنش برشی ماکسیمم درون صفحه‌ای با شعاع دایره برابر است:

مقدار زاویه ACS₁ از نقطه A تا نقطه S₁ از رابطه 2θ_s1=90-2θ_p1 به دست می‌آید:

بنابراین، صفحه دربرگیرنده تنش‌های برشی ماکسیمم در المان تنش به اندازه θ_s1=-25.7 با محور x اختلاف زاویه دارد. به دلیل تعیین این زاویه در جهت ساعتگرد بر روی دایره، علامت آن منفی است. شکل زیر، وضعیت تنش‌های برشی ماکسیمم بر روی المان تنش را نمایش می‌دهد.

توجه داشته باشید که مقدار تنش‌های نرمال اعمال شده بر روی صفحه دربرگیرنده تنش‌های برشی ماکسیمم با مقدار تنش نرمال میانگین (σ_aver) برابر است. σ_aver نیز با طول مرکز دایره بر روی محور افقی برابری می‌کند.

مثال 3

وضعیت تنش نقطه‌ای بر روی سطح میله یک ژنراتور را در نظر بگیرید که تحت تنش σy=10MPa ،σ_x=-50MPa و τ_xy=-40MPa قرار دارد (شکل زیر).

با استفاده از دایره مور، مقادیر مربوط به هر یک از کمیت‌های زیر را تعیین کنید:

• الف) تنش‌های اعمال شده بر روی المان دوران یافته تحت زاویه θ=45
• ب) تنش‌های اصلی
• ج) تنش‌های برشی ماکسیمم

رسم دایره مور

برای رسم دایره مور مانند مثال قبل عمل می‌کنیم. به این ترتیب، مقادیر مثبت σ_x1 در سمت راست و مقادیر مثبت τ_x1y1 در بخش پایینی دستگاه مختصات قرار می‌گیرند.

شکل زیر، دایره نهایی و مؤلفه‌های تنش مربوط به این مسئله را نمایش می‌دهد (محل قرارگیری دایره در این مثال را با مثال‌های قبلی مقایسه کنید).

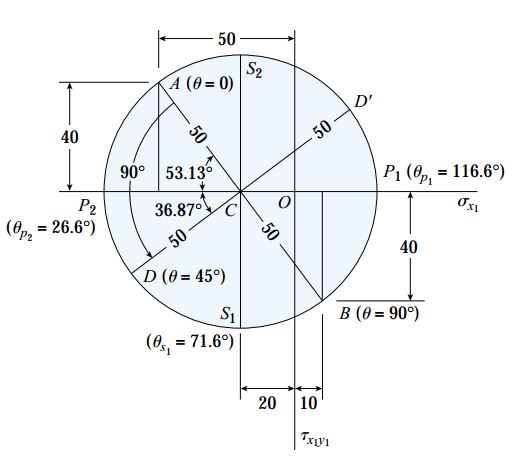
مرکز دایره (C) بر روی محور σ_x1 برابر است با:

مقادیر تنش‌های موجود بر روی صفحه x در المان تنش با مختصات نقطه A در زاویه θ=0 بر روی دایره مور مشخص می‌شوند:

مقادیر تنش‌های موجود بر روی صفحه y در المان تنش با مختصات نقطه B در زاویه θ=90 بر روی دایره مور مشخص می‌شوند:

با توجه به مقادیر به دست آمده، دایره گذرنده از نقاط A و B به مرکزیت C و شعاع R رسم می‌شود. مقدار شعاع دایره برابر است با:

تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=45

با مشخص کردن مختصات نقطه D که به اندازه 2θ=90 بر روی دایره مور با نقطه A اختلاف دارد، مقادیر تنش‌های موجود بر روی المان دوران یافته تحت زاویه θ=45 تعیین می‌شوند. به منظور مشخص کردن این مختصات، در ابتدا باید زاویه بین خط CD با بخش منفی محور σ_x1 (زاویه DCP₂) و زاویه بین خط CA با بخش منفی محور σ_x1 (زاویه ACP₂) را تعیین کنیم. با در نظر گرفتن هندسه دایره داریم:

بنابراین، مختصات نقطه D در زاویه 2θ=90 بر روی دایره برابر است با:

به همین ترتیب، مختصات نقطه 'D در زاویه 2θ=270 بر روی دایره نیز به صورت زیر خواهد بود:

شکل زیر، وضعیت تنش‌های المان دوران یافته تحت زاویه θ=45 را نمایش می‌دهد.

تنش‌های اصلی

با توجه به دایره مور، تنش اصلی بزرگ (نقطه P₁) برابر است با:

با اندازه‌گیری زاویه 2θ_p1 از نقطه A تا نقطه P₂ در جهت پادساعتگرد (زاویه ACP₁) داریم:

بنابراین، صفحه دربرگیرنده تنش اصلی بزرگ در المان تنش به اندازه θ_p1=116.6 نسبت به محور x اختلاف زاویه دارد. مقدار تنش اصلی کوچک (P₂) نیز با همین روش محاسبه می‌شود:

زاویه بین نقطه P₂ و نقطه A بر روی دایره (2θ_p2) برابر با 53.13 درجه است. به این ترتیب، صفحه اصلی دوم به اندازه زاویه θ_p2=26.6 درجه نسبت به محور x اختلاف دارد. شکل زیر، وضعیت تنش‌های اصلی بر روی المان تنش را نمایش می‌دهد.

تنش‌های برشی ماکسیمم

تنش‌های برشی ماکسیمم بر روی دایره مور با نقاط S₁ و S₂ نمایش داده می‌شوند. مقدار این تنش‌ها با شعاع دایره برابر است:

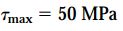
زاویه بین نقطه A تا نقطه S₁ (زاویه ACS₁)، جهت‌گیری نقطه S₁ را نمایش می‌دهد:

زاویه θ_s1=71.6، معرف جهت‌گیری صفحه دربرگیرنده تنش برشی ماکسیمم مثبت در المان تنش خواهد بود. مقدار تنش برشی ماکسیمم منفی (S₂) با مقدار S₁ برابر است. شکل زیر، وضعیت تنش‌های برشی ماکسیمم بر روی المان تنش را نمایش می‌دهد.

^^