آزمون یو من ویتنی (Mann–Whitney U) در SPSS – راهنمای کاربردی
یکی از روشهای «آزمون فرض آماری» (Statistical Hypothesis Testing) در بین دو جامعه یا گروه مستقل، «آزمون یو من ویتنی» (Mann-Whitney U) است که توسط دانشمندان آمار به نامهای «هنری مَن» (Henry Mann) و «دونالد ویتنی» (Donald Ransom Whitney) در سال ۱۹۴۷ طی مقالهای ارائه شده. این آزمون از گروه روشهای ناپارامتری است و بنابراین نسبت به مشابه پارامتری خود زمانی که دادهها دارای توزیع نرمال باشند، از توان کمتری برخوردار است. ولی زمانی که اندازه نمونه کوچک یا چولگی توزیع دادهها زیاد باشد بهتر است از آزمونهای ناپارامتری مانند این آزمون برای مطابقت بین دو توزیع استفاده شود. در این نوشتار به بررسی این آزمون و خصوصیات آن پرداخته و برای اجرای آن از نرمافزار محاسبات آماری SPSS استفاده خواهیم کرد. پیشفرضها و شرایط استفاده از این آزمون نیز در این متن مرور و مورد بررسی قرار داده خواهند شد.




از آنجایی که برای درک بهتر این نوشتار باید از قبل اطلاعاتی در مورد استنباط و آزمون فرض آماری داشته باشید، بهتر است به عنوان پیشنیاز مطالب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری را مطالعه کنید. همچنین خواندن نوشتار آزمون علامت (Sign Test) — به زبان ساده و آزمون دو جمله ای (Binomial Test) در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.
آزمون یو من ویتنی
فرض کنید که دو گروه یا دو جامعه آماری مستقل در اختیار دارید. به کمک آزمون من ویتنی میتوانید جدایی یا وابستگی بین این دو گروه یا جامعه را مورد بررسی قرار دهید. برای مثال با استفاده از این آزمون میتوانید نشان دهید که میزان درآمد در بین زنان و مردان یکسان است یا خیر! واضح است که در اینجا درآمد به عنوان متغیر وابسته یا ویژگی است که قرار است بین دو جامعه مستقل (زنان و مردان) مورد سنجش قرار بگیرد. به این ترتیب میتوان آزمون من ویتنی را مشابه آزمون T دو نمونهای مستقل در نظر گرفت. با این تفاوت که معیار سنجش در اینجا میانگین دو جامعه نخواهد بود بلکه از رتبهها و مجموع آنها استفاده خواهد شد.
از آنجایی که باید توزیع احتمالی در بین دو گروه مستقل مورد بررسی قرار گیرند، میتوان دادهها را به شکلی در نظر گرفت که یک متغیر وابسته (مانند درآمد) و یک متغیر مستقل (مانند جنسیت) که به صورت متغیر طبقهای است، در آزمون نقش داشته باشند. به کمک متغیر مستقل، جامعه به دو گروه تقسیم شده و یکسان بودن توزیع احتمالی برای متغیر وابسته در هر دو گروه مورد سنجش قرار میگیرد.
شرایط آزمون من ویتنی
قبل از انجام این آزمون باید از شرایط و نحوه بررسی آنها مطمئن شویم در غیر اینصورت نتایج حاصل از آزمون من ویتنی صحت نخواهد داشت. در ادامه با چهار شرطی اصلی برای انجام این آزمون آشنا خواهید شد.
- متغیر وابسته (Dependent Variable) باید به صورت ترتیبی یا سطوحی از متغیر عددی باشد. برای مثال میتوان متغیرهایی با مقیاس طیف لیکرت را (مثلا با ۵ سطح) به عنوان متغیر وابسته در نظر گرفت. البته در این آزمون میتوانید از متغیرهای عددی مانند درآمد، وزن، بهره هوشی و ... نیز استفاده کنید.
- متغیر مستقل باید بیانگر دو طبقه یا دو وضعیت باشد. در نتیجه متغیرهای طبقهای (ترتیبی یا اسمی) که به صورت دو وضعیتی باشند، میتوانند به عنوان متغیر مستقل معرفی شوند. برای مثال جنسیت (زن- مرد)، وضعیت اشتغال (شاغل- بیکار) از گروه متغیرهای طبقهای یا دو وضعیتی هستند که قابلیت استفاده در آزمون من ویتنی را دارند.
- نمونهها از هر دو جامعه باید به صورت تصادفی باشد. به این ترتیب نمونهگیری باید به شکل تصادفی در هر گروه انجام شود. بنابراین نباید یک مشاهده بیش از یک بار و یا در بیش از یک گروه به کار گرفته شود. از طرفی استقلال یا عدم وابستگی بین گروه یا جامعهها نیز از فرضیه اصلی این آزمون محسوب میشود.
- از آنجایی که این آزمون یک روش ناپارامتری است، فرض بر این است که دادهها دارای توزیع نرمال نیستند یا حداقل در مورد توزیع آنها اطلاعاتی در دست نیست. زیرا اگر دادهها دارای توزیع نرمال یا تقریبا نرمال باشند، روشهای پارامتری بهتر از آزمون من ویتنی پاسخ داده و توان آزمون بزرگتری دارند. بنابراین بهتر است از آزمونها پارامتری برای انجام مقایسه توزیع دو جامعه استفاده کرد.
بهتر است قبل از انجام هر کاری، ابتدا در مورد توزیع دادهها یک بررسی انجام داده و نمودار فراوانی متغیر وابسته را به تفکیک گروهها (متغیر مستقل) ترسیم کنیم.
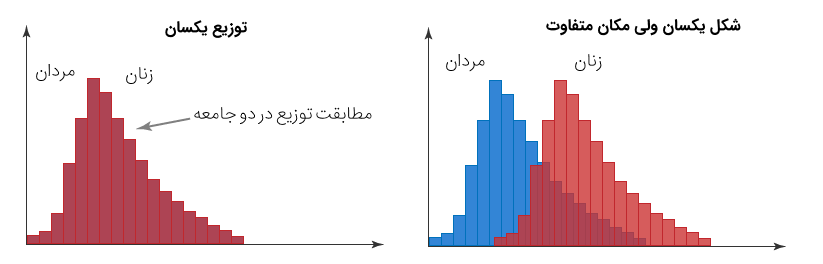
در نمودارهای بالا، نمودار فراوانی دو جامعه ترسیم شدهاند. در سمت چپ، دو جامعه دارای توزیع یکسانی هستند ولی در تصویر سمت راست، شکل توزیع یکسان ولی در یک یا چند پارامتر، متفاوت هستند. به نظر میرسد که «پارامتر مکان» (Location Parameter) در این دو توزیع یکسان نیست و برای مثال ممکن است سطح درآمدی زنان نسبت به مردان از میانگین یا میانه بزرگتری برخودار باشد.
زمانی که توزیع دادهها را در بین دو گروه بررسی میکنید، بسیار بعید است که توزیع احتمالی برای آنها به مانند یکدیگر باشد ولی ممکن است که اختلاف در بین توزیع احتمالی دو گروه ناشی از اختلاف در معیار مرکزی باشد. به این ترتیب به نظر میرسد که دو گروه در شکل توزیع یکسان ولی در پارامتر مکان اختلاف داشته باشند. فرض یکسان بودن توزیع در استنباط آماری به عنوان فرض صفر در نظر گرفته میشود. در آزمون من ویتنی، با استفاده از مقایسه میانگین رتبهها، میتوان همتوزیع بودن و یکسان بودن پارامتر مکان را مشخص کرد.
بنابراین اگر مقادیر مربوط به گروه اول و مقادیر گروه دوم باشند، تحت فرض صفر (برابری توزیع هر دو گروه) خواهیم داشت:
و تحت فرض مقابل نیز رابطه زیر برقرار است.
به این ترتیب به کمک آزمون من ویتنی قادر خواهیم بود که یکسان بودن دو توزیع احتمالی را از لحاظ شکل و مکان مورد بررسی قرار دهیم. در ادامه این مطلب برای انجام این امر از نرمافزار محاسبات آماری SPSS کمک خواهیم گرفت.

نحوه انجام آزمون من ویتنی و آماره آزمون
فرض کنید اندازه نمونه از جامعه اول برابر با و برای جامعه دوم نیز باشد. همچنین در نظر بگیرید که مقادیر این دو گروه در یک مجموعه قرار گرفته و رتبههای مربوط به مقدارها، از کم به زیاد تعیین شده باشد. در این صورت اگر مجموع رتبههای گروه اول و مجموعه رتبههای گروه دوم باشد آماره آزمون را به صورت زیر تعریف میکنیم.
نکته: مشخص است که اگر گروه اول دارای مقدارهای کوچکتر از گروه دوم باشد همه رتبههای کوچکتر به آن گروه تعلق خواهد داشت و به این ترتیب مجموع رتبههای مربوط به گروه اول براساس تصاعد حسابی به صورت زیر خواهد شود.
در نتیجه هر چقدر مقدار کوچک باشد رای به یکسان نبودن توزیع دو گروه خواهیم داد. از طرفی میتوانیم ملاک را گروه ۲ در نظر بگیریم. در نتیجه میتوانیم مجموع رتبهها را برحسب این گروه محاسبه کنیم.
با توجه به کوچک بودن مقدار نیز رای عدم یکسان بدون توزیعها در بین دو گروه خواهیم داد. اگر فرض صفر را به صورت یکسان بودن توزیع دو گروه در نظر بگیریم، به این ترتیب میتوان گفت که کوچک بودن یا دلیلی بر رد صفر خواهد بود. باید توجه داشت که مجموع و ثابت و برابر با خواهد بود، زیرا:
بنابراین اگر باشد، واضح است که است. با اندکی محاسبات جبری خواهیم داشت:
به این ترتیب میتوان مقدار را برحسب یا برعکس محاسبه کرد. از طرفی برای آماره آزمون میتوان هم از و هم از استفاده کرد.
مثال ۱
فرض کنید گروهی از خانمها (F) و آقایان (M) را که به دیابت مبتلا هستند به عنوان نمونه تصادفی در نظر گرفتهایم. از هر یک از آنها طول سالهای ابتلا به دیابت را پرسیدهایم. میخواهیم تصمیم بگیریم که سن دیابت در بین خانمها و آقایان یکسان است یا خیر؟ مقدار آماره را بر اساس این مشاهدات محاسبه میکنیم. مشخص است که دو جامعه خانم و آقا (متغیر مستقل) وجود دارد که مشاهداتی از آنها را براساس نمونه، اندازهگیری کردهایم.
| سن | جنسیت | رتبه M | رتبه F |
| 11 | F | 1 | |
| 12 | F | 2 | |
| 16 | M | 3 | |
| 17 | F | 4 | |
| 19 | M | 5 | |
| 20 | F | 6 | |
| 22 | M | 7 | |
| 24 | M | 8 | |
| 29 | M | 9 | |
| تعداد | 5 | 4 | |
| مجموع رتبهها (R) | 32 | 13 | |
| U |
البته برای محاسبه احتمال جدولهای مختلفی برحسب توزیع این آماره وجود دارد ولی میتوان از توزیع مجانبی که به صورت نرمال با میانگین و انحراف معیار نیز استفاده کرد. بنابراین آماره آزمون را به صورت زیر خواهیم نوشت. این آماره دارای توزیع نرمال با میانگین صفر و واریانس ۱ است.
در ادامه به بررسی محاسبات و اجرای این آزمون در محیط SPSS خواهیم پرداخت.
آزمون یو من ویتنی در SPSS
در بخش شرایط آزمون من ویتنی خواندید که باید از دو متغیر برای اجرای این آزمون استفاده کرد. متغیر وابسته که براساس آن، توزیع و رتبهها محاسبه میشود و متغیر مستقل که وظیفه تفکیک و تشخیص دو جامعه را به عهده دارد. به این ترتیب باید هنگام به کار گیری SPSS برای انجام این آزمون، این متغیرها تعریف و مقدار دهی شوند. در ادامه براساس دو مثال کار تحلیل و انجام این آزمون را در محیط SPSS دنبال میکنیم.
مثال ۲
براساس دادههای مربوط به مثال ۱ قرار است توزیع سن ابتلا به دیابت را در بین خانمها و آقایان مورد بررسی قرار دهیم. ابتدا دادهها را مطابق با شرایط اجرای آزمون (متغیر مستقل و وابسته) به مانند تصویر زیر ثبت میکنیم.
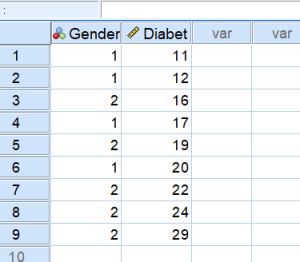
همانطور که مشخص است در متغیر Gender برای خانمها از کد ۱ و برای آقایان از کد ۲ استفاده شده است. حال به منظور دسترسی به آزمون ناپارامتری من ویتنی مسیر زیر را طی کنید. البته این مسیر دستیابی به دستور اجرای این آزمون در نسخههای قدیمی SPSS وجود داشته که برای هماهنگی با آنها در نسخههای جدید در قسمت «پنجرههای قدیمی» (Legacy Dialog) قرار گرفته است.
Analyze -> Nonparameteric Test -> legacy Dialogs -> 2 Independent Samples...
پس از طی کردن این مسیر، پنجرهای به مانند تصویر زیر ظاهر میشود که کافی است برای اجرای آزمون من ویتنی، تنظیمات را مطابق با تصویر زیر انجام دهید. مشخص است که متغیر Diabet باید به عنوان متغیر وابسته در قسمت Test Variable List قرار بگیرد. از طرفی متغیر مستقل که جنسیت (Gender) است در کادر Grouping Variable قرار گرفته تا گروهها یا دو جامعه آماری را مشخص کند. با انتخاب دکمه Define Groups قادر هستید که سطوح یا مقدارهایی را مشخص کنید که قرار است تفکیک طبقات را تعیین کنند. همانطور که میبینید، مقدار 1 و 2 برای مشخص کردن دو جامعه خانمها و آقایان به کار رفته است.
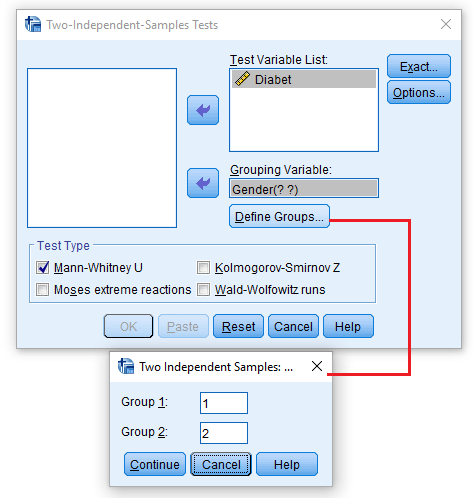
با توجه به توزیع دقیق یا توزیع مجانبی آماره U میتوانید آزمون من ویتنی را انجام دهید. این کار به کمک دکمه Exact صورت خواهد گرفت. همچنین تنظیمات دیگر مانند نمایش آمار توصیفی و چگونگی برخورد با «دادههای گمشده» (Missing Values) نیز از امکانات دیگری است که در پنجره اصلی این آزمون قرار گرفته است و به کمک دکمه Options قابل دستیابی است. تصویر مربوط به تنظیمات هر یک از این پنجرهها در ادامه قابل مشاهده است.
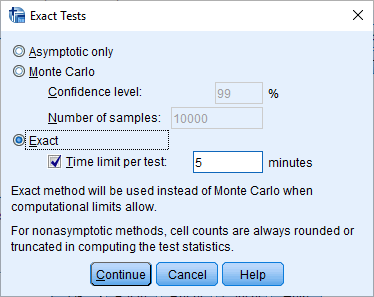
مشخص است که با توجه به اندازه نمونه کوچک در این مثال، از توزیع دقیق آماره آزمون (U) استفاده شده است. اگر اندازه نمونه بزرگ باشد ممکن است آزمون دقیق زمان زیادی بگیرد. به همین دلیل حداکثر زمان برای اجرای آزمون در کادر Time limit per test را ۵ دقیقه به عنوان پیشفرض در نظر گرفتهاند. البته میتوانید به دلخواه این زمان را تغییر دهید. اگر اندازه نمونه بزرگ باشد و بخواهید در زمان کوتاهتری نتایج را بدست آورید از گزینه Asymptotic only استفاده کنید، در این صورت توزیع مجانبی آماره برای انجام آزمون به کار خواهد رفت. همچنین برای تعیین واریانس برآورد نیز میتوان از روش مونتکارلو استفاده کرد تا اگر اندازه نمونه کوچک است بتوان برآورد مناسبتر و با دقت بیشتری را بوسیله شبیهسازی مونتکارلو بدست آورد.
همانطور که در تصویر بالا مشاهده میکنید، با انتخاب گزینه Descriptive، آمار توصیفی نظیر تعداد (N)، میانگین (Mean)، انحراف استاندارد (Standard Deviation)، حداقل (Minimum) و حداکثر (Maximum) متغیر وابسته (Diabet) ظاهر میشود. گزینه Quantiles نیز باعث ظاهر شدن چارکها خواهد شد. همچنین در قسمت Missing Values مشخص میکنید که اگر چند متغیر وابسته در آزمون به کار روند، با وجود یک یا چند مشاهده با مقدار گمشده چه وضعیتی برای حذف آنها رخ دهد. اگر گزینه Exclude cases test-by-test را انتخاب کنید، مشاهدات مربوط به هر متغیر آزمون که دارای مقدار گمشده هستند، حذف میشوند ولی اگر گزینه Exclude cases listwise را فعال کنید، آزمون برای مشاهداتی اجرا خواهد شد که در هیچ یک از متغیرها مقدار گمشده نداشته باشند. با فشردن دکمه Continue در این پنجرههای فرعی به صفحه اصلی آزمون بازگشته و با انتخاب دکمه OK، نتایج اجرای آزمون من ویتنی در پنجره Output مطابق با تصویر زیر ظاهر میشود.
برای اجرای این آزمون در محیط Syntax نیز کافی است که کدهای زیر را به کار ببرید.
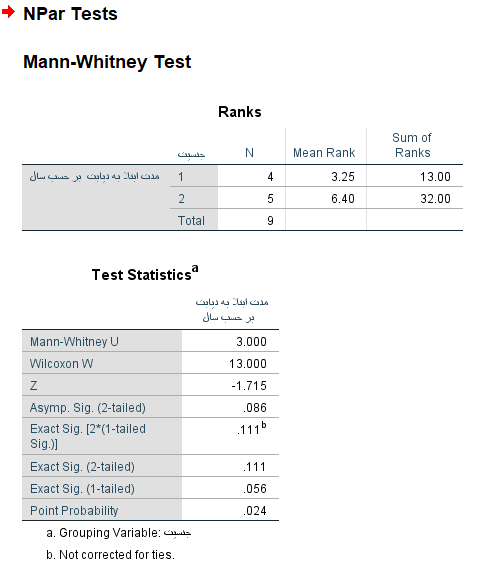
اینک به تفسیر خروجی میپردازیم. همانطور که در پنجره Output میبینید، براساس مقدار احتمال (p-Value) که در SPSS به نام Sig نمایش داده میشود، در آزمون دو طرفه () داریم که در سطح معنیداری دلیلی بر رد فرض صفر وجود ندارد که نشانگر یکسان بودن توزیع دادهها است. همچنین در آزمون یک طرفه () نیز باز هم فرض صفر رد نمیشود. این نتایج در مقدار Sig مربوط به آماره مجانبی (Asymp. Sig) نیز مورد تایید است زیرا مقدار Asymp. Sig=0.086 از 0.05 که سطح آزمون یا احتمال خطای نوع اول است بزرگتر است. از طرفی مشخص است که مقدار آماره آزمون برابر است با ۳ نشان دهنده محاسبه آماره براساس رتبههای آقایان است.
مثال ۳
در این مثال به کمک روش جدیدی که برای اجرای آزمونها در SPSS ایجاد شده است، آزمون من ویتنی را اجرا خواهیم کرد. البته با توجه به تعریف صحیحی که برای متغیرها انجام دادهایم، میتوانیم انتخاب نوع آزمون را به طور خودکار به SPSS بسپاریم. به این منظور مراحل زیر را برای دسترسی به این آزمون به کار میبریم.
Analyze -> Nonparameteric Test -> Independent Samples...
با طی کردن این مسیر پنجره مربوط به اجرای آزمون دو نمونهای ظاهر میشود. به این ترتیب با تنظیماتی که مطابق با تصویرهای زیر خواهید دید، میتوانید آزمون من ویتنی را اجرا کنید.
در برگه دوم به نام Fields نیز با انتخاب Diabet در قسمت Test Fields و Gender در Groups، متغیرهای مستقل و وابسته را مشخص کردهایم. به این ترتیب مشخص میشود که قرار است آزمون یکسان بودن توزیع جامعه خانمها و آقایان از لحاظ طول دوره ابتلا به دیابت مورد بررسی قرار گیرد.
همچنین در بخش انتهایی یعنی برگه Settings نیز با انتخاب گزینه Customize tests و Mann-Whitney U، نوع آزمون را مشخص میکنید.
با انجام این کارها میتوانید خروجی را با فشردن دکمه Run ظاهر کنید. البته اگر قصد دارید کد دستوری برای انجام این عملیات را در یک فایل دستوری Syntax ثبت و اجرا کنید کافی است با فشردن دکمه Paste کدها را ایجاد کنید.
با ذخیره کردن این کدها، میتوانید هر زمان براساس این متغیرها مجدد آزمون را با توجه به تنظمیات صورت گرفته، اجرا کنید. خروجی آزمون من ویتنی در این حالت به صورت زیر خواهد بود.

اگر بر روی این خروجی دوبار کلیک کنید، وارد پنجره Model Viewer خواهید شد که اطلاعات بسیار بیشتری نسبت به خروجی قدیمی SPSS ارائه میکند. همانطور که در کادر سمت راست میبینید فراوانی مربوط به دو جامعه به همراه میانگین رتبهها (Mean Rank) ظاهر شده است. همچنین مقدار U نیز با نام Test Statistics و مقدار 17.000 دیده میشود. پس مشخص است که مقدار U برحسب رتبه آقایان محاسبه شده است. با توجه به مقدار Sig= 0.111 مشخص میشود که دلیلی برای رد فرض صفر وجود ندارد در نتیجه به نظر میرسد جنسیت عامل تعیین کنندهای در طول دوره بیماری دیابت نخواهد بود.

نکته: همانطور که مشخص است روش قدیمی انجام آزمون من ویتنی، ملاک محاسبه آماره U را براساس رتبههای اولین گروه (خانمها) بدون توجه به مقدار گروه، انجام داده است در حالیکه در روش جدید این آماره برحسب رتبه گروه آقایان محاسبه شده که دارای برچسب یا مقدار بزرگتری هستند. مشخص است که مقدار کد برای خانمها برابر با 1 و برای آقایان نیز 2 در نظر گرفته شده بود.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش آزمون آماری و پی مقدار (p-value)
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
- آزمون دو جمله ای (Binomial Test) در SPSS — راهنمای کاربردی
- آزمون علامت (Sign Test) — به زبان ساده
^^













تمامی نتایج sigدر داده های من ک از آزمون بومن ویتنی بدست اومد بالای0/05بود.حالا هر گروهی که عدد بالاتری داشت. ینی برتری نسبت به گروه دیگر دارد؟
عالی بوددست شمادرد نکنه .پیشنهاد می کنم تمرین ویا مثال تاانتها حل شود سپس به بحث جدید وارذ شویم .سپاس
با سلام
در بخش تفسیر نتایج بهتر توضیح داده شود و نتایج تفسیر شود بهتر خواهد بود. باتشکر از زحمات شما
با سلام خیلی ممنون از توضیحات مفیدتون
یک سوال داشتم، از این آزمون برای بررسی نقطه تغییر یا جهش در سری های زمانی هم میتونیم استفاده بکنیم؟؟
ممنون میشم راهنمایی بفرمایید.
سلام و سپاس از مطلب خوبتون
۱_ببخشید ازین آزمون میشه برای بررسی اثرگذاری وضعیت اقتصادی (سه سطح) بر روی رفتار صرفه جویی (۱۲ سوال لیکرت ۵ طیفی) یک گروه مثلا زنان استفاده کرد؟
۲- اگه بخواییم سطح تحصیلات و وضعیت اقتصادی و سن رو هم اضافه کنیم ببینم چه اثری بر رفتار دارد چه آزمونی برای همه اینا مناسب است؟