تابع درست نمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

یکی از مهمترین مسائل در تحقیقات آماری، برآورد پارامترهای مدل است. این امر، ممکن است به کمک تابع درستنمایی صورت گیرد. از منظر «تحلیلگران فراوانی» (Frequentist Inference)، تابع درستنمایی، صحیح‌ترین راه برای رسیدن به هدف محسوب می‌شود. بسیاری از برآوردها، در تجزیه و تحلیل‌های آماری به کمک تابع درستنمایی صورت می‌پذیرد زیرا درک و شهود بیشتری در به کارگیری این روش وجود دارد.

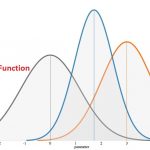
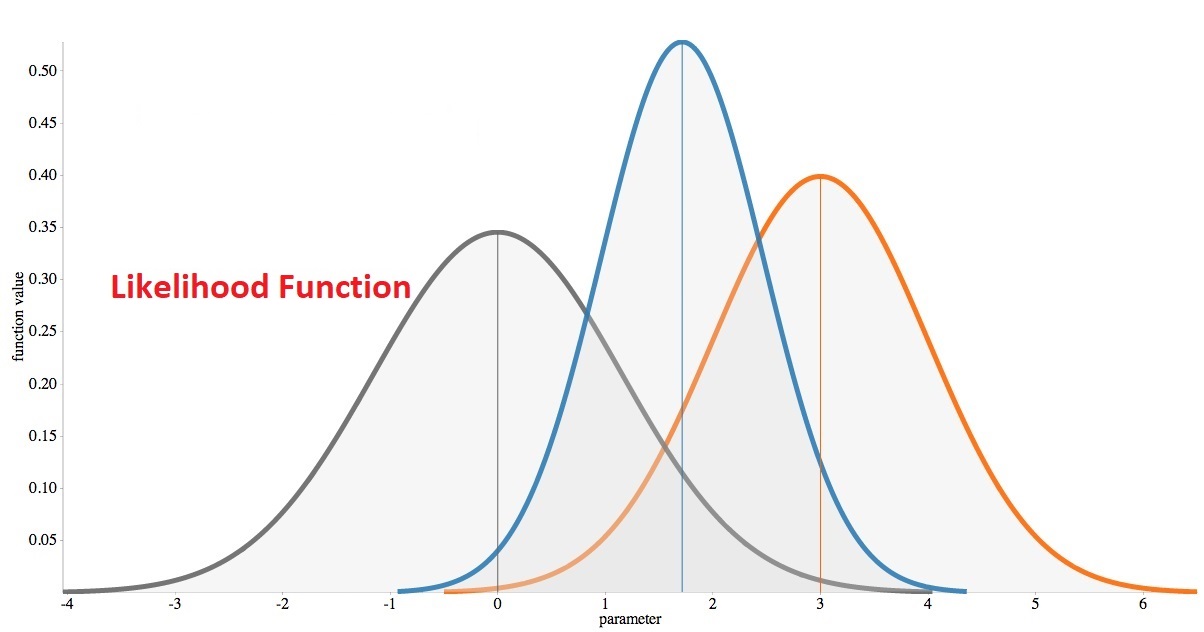
گاهی به تابع درستنمایی همان تابع احتمال نیز می‌گویند ولی باید توجه داشت زمانی که در مورد احتمال رویدادی (بدون هیچ مشاهده‌ای) با توجه به معلوم بودن مدل و پارامترهای آن صحبت می‌کنیم، واژه تابع احتمال را به کار می‌گیریم و زمانی که در مورد مقدارهای محتمل برای پارامتر مدل با توجه به مشاهدات انجام شده تصمیم‌گیری می‌کنیم، از تابع درستنمایی بهره می‌بریم. البته در مباحت مربوط به «استنباط بیزی» (Bayesian Inference) با توجه به احتمال شرطی، تابع درستنمایی تعریف شده و به منظور برآورد پارامترهای مدل‌های آماری به کار گرفته می‌شود.

در این مطلب ابتدا در مورد تابع درستنمایی صحبت می‌کنیم و برای چند توزیع معروف، تابع درستنمایی را با استفاده از محاسبات انجام می‌دهیم. در انتها با استفاده از مثال‌هایی، پارامترهای چند توزیع را به کمک روش بیشینه‌سازی تابع درستنمایی برآورد می‌کنیم. بدیهی است که این کار بدون مقدارهای مشاهده شده از یک نمونه تصادفی امکان‌پذیر نیست.

پیشنهاد می‌شود، برای درک بهتر این نوشتار، با مفاهیم تابع چگالی و متغیر تصادفی که در مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و آزمایش تصادفی، پیشامد و تابع احتمال آمده است، آشنا باشید. در مثال‌هایی که در ادامه خواهید دید، از متغیرهای تصادفی با توزیع دو جمله‌ای و پواسن استفاده شده است، به همین دلیل، مطالعه مطلب‌های متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده و متغیر تصادفی و توزیع پواسن — به زبان ساده خالی از لطف نیست.

تابع درستنمایی

اولین بار «رونالد فیشر» (Ronald Fisher)، آمارشناس و دانشمند برجسته انگلیسی، واژه درستنمایی (Likelihood) را استفاده کرد. این واژه در مقاله معروف وی به نام «مبانی ریاضیات در آمار نظری» (On the mathematical foundations of theoretical statistics) که در سال 1922 میلادی منتشر شد برای اولین بار به کار رفت. روشی که او در این مقاله به کار برد، امروزه هم توسط بسیاری از آمارشناسان به منظور برآورد پارامترهای مدل مورد استفاده قرار می‌گیرد.

فیلم آموزش آمار ریاضی ۱ – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

آنان در این گونه مسائل، براساس یک نمونه تصادفی محاسبات را انجام می‌دهند و در بسیاری از موارد از یک نمونه تصادفی هم‌توزیع و مستقل کمک می‌گیرند. بنابراین بهتر است ابتدا با اصطلاحات نمونه تصادفی هم‌توزیع و مستقل بیشتر آشنا شویم.

معمولا در نمونه‌گیری تصادفی، فرض بر این است که هر یک از اعضای نمونه از یک جامعه انتخاب می‌شوند و همچنین شانس انتخاب در نمونه نیز برای همه اعضای جامعه وجود دارد. از طرفی انتخاب یک عضو بر روی احتمال انتخاب اعضای دیگر نیز تاثیر گذار نخواهد بود. این شرایط نمونه‌گیری کمک می‌کند که برآوردها و تحلیل‌های آماری حاصل از آن، بدون اریب باشند. به این ترتیب در بحث برآوردیابی به کمک تابع درست نمایی نیز از چنین نمونه‌ای بیشترین بهره را می‌بریم. حال با توجه به این توضیح، جملات و اصطلاحاتی که در ادامه خواهند آمد، ملموس‌تر خواهند بود.

تابع چگالی توام (Joint Density Function)

زمانی که متغیر تصادفی Z، «چند بعدی» (Multi-Dimensional) باشد، تابع توزیع احتمال آن براساس تابع توزیع احتمال مولفه و ارتباطی که بین آن‌ها برقرار است، نوشته می‌شود. برای مثال اگر $$Z=(X,Y)$$ یک متغیر تصادفی دو بعدی از توزیع نرمال دو متغیره باشد، تابع توزیع احتمال آن، که گاهی تابع چگالی توام نیز خوانده می‌شود، به صورت زیر خواهد بود. (X مولفه اول یا بعد اول و Y مولفه دوم یا بعد دوم است.)

$$f_{Z}(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}+{\frac {(y-\mu _{Y})^{2}}{\sigma _{Y}^{2}}}-{\frac {2\rho (x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right]\right)}$$

در رابطه بالا، $$\sigma_{X}$$ و $$\sigma_{Y}$$ انحراف استاندارد در بعد اول و دوم هستند. همچنین $$\rho$$ نیز ضریب همبستگی بین بعد اول و دوم را نشان می‌دهد. واضح است که $$\mu_x$$ و $$\mu_y$$ نیز میانگین در بعد اول و دوم هستند.

نکته: تابع احتمال برای هر یک از مولفه‌های متغیر تصادفی چند بعدی را «توزیع احتمال حاشیه‌ای» (Marginal Probability Distribution) نیز می‌نامند.

در صورتی که مولفه‌های هر بعد از متغیر تصادفی، از یکدیگر مستقل باشند تابع چگالی توام را می‌توان به صورت حاصلضرب تابع احتمال‌های حاشیه‌ای نوشت. در این صورت برای n متغیر تصادفی مستقل، تابع توزیع احتمال توام براساس تابع احتمال‌های حاشیه‌ای به صورت زیر در خواهد آمد:

$$\large f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)=f_{X_1}(x_1)f_{X_2}(x_2)\ldots f_{X_n}(x_n)$$

برای متغیر تصادفی نرمال دو متغیره (دو بعدی) در صورت استقلال هر بعد (مولفه) آن، رابطه زیر بین توزیع‌های حاشیه‌ای و توزیع توام وجود دارد. در اینجا توزیع توام X و Y را به صورت $$f_{X,Y}(x,y)$$ و توزیع حاشیه‌های را با $$f_X(x)$$ و $$f_{y}(y)$$ نشان داده‌ایم.

$$\large f_{X,Y}(x,y)=f_X(x)f_Y(y)$$

که با جایگذاری تابع چگالی احتمال در هر بعد، تابع توزیع احتمال توام برحسب تابع احتمال حاشیه‌ای، به صورت زیر در خواهد آمد:

 $$\large {\displaystyle f_{X,Y}(x,y)={\dfrac {1}{2\pi\sigma _{X}\sigma _{Y}}}}\exp \left((-{\dfrac {1}{2}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}\right])+(-{\frac {1}{2}}\left[{\frac {(y-\mu _{Y})^{2}}{\sigma _{Y}^{2}}}\right])\right)$$

نمونه تصادفی مستقل و هم‌توزیع (iid)

نمونه‌های $$X_1,X_2,\ldots,X_n$$ را مستقل و هم‌توزیع می‌نامند، اگر تابع احتمال توام این نمونه‌های تصادفی با حاصلضرب تابع احتمال آن‌ها برابر باشد. به این ترتیب برطبق تابع چگالی توام و استقلال متغیرهای تصادفی که در بالا گفته شد، می‌توان تابع احتمال (چگالی) توام $$X_1,X_2,\ldots,X_n$$ را به صورت زیر نوشت.

فیلم آموزش آمار ریاضی ۲ – آزمون فرض در فرادرس

کلیک کنید

توجه داشته باشید که در اینجا $$f_{X_i}(x)$$ تابع احتمال مربوط به متغیر تصادفی iام است.

$$\large f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)=\prod_{i=1}^n f_{X_i}(x_i)$$

از طرفی اگر این نمونه‌ها، هم‌توزیع باشند به این معنی خواهد بود که تابع احتمال همه یکسان است. در نتیجه می‌توان گفت $$f_{X_i}(x)=f_{X}(x)$$. در این فرضیات، تابع احتمال توام این نمونه تصادفی به صورت ساده‌تری که در زیر نوشته شده‌ است درخواهد آمد.

$$\large f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)=\prod_{i=1}^n f_{X}(x_i)$$

در چنین حالتی، نمونه تصادفی را «مستقل و هم‌توزیع» (Independent and Identically Distribution) می‌نامند.

نکته: گاهی به جای استفاده از عبارت طولانی مستقل و هم‌توزیع از حروف اختصاری iid‌ کمک گرفته می‌شود که سرکلمه‌های مربوط به عبارت لاتین آن است.

محاسبه تابع درست نمایی

فرض کنید $$X_1,X_2,\ldots,X_n$$ نمونه تصادفی nتایی هم‌توزیع و مستقل (iid) از یک متغیر تصادفی با تابع احتمال $$f_X(x)$$ باشند. آنگاه $$L(\theta)$$ را تابع درست نمایی این نمونه تصادفی برحسب پارامتر مجهول جامعه یعنی $$\theta$$ می‌نامند و می‌نویسند:

$$\large L(\theta)=f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)=\prod_{i=1}^n f_{X}(x_i)$$

البته اگر نمونه‌های تصادفی مستقل و هم توزیع نباشند، تابع درستنمای همان تابع توزیع توام نمونه تصادفی خواهد بود. یعنی می‌توان آن را به صورت زیر نمایش داد:

$$\large L(\theta)=f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)$$

نکته: به نظر می‌رسد که تابع توزیع توام همان تابع درست نمایی باشد، ولی باید توجه داشت که تابع توزیع توام، تابعی از نمونه تصادفی با فرض ثابت بودن پارامترهای توزیع است، در حالی‌که تابع درست نمایی، همان تابع توزیع توام است اگر به پارامترها به دید متغیر تابع نگاه شود و نمونه تصادفی در آن ثابت باشد.

مثال ۱

فرض کنید $$X_1,X_2,\ldots,X_n$$ یک نمونه تصادفی از توزیع دو جمله‌ای با پارامترهای ۱۰ و p باشند. یعنی می‌توانیم بنویسیم $$X_i \sim B(10,p)$$ است. در این حالت مثلا $$X_i$$ شاید تعداد شیرهای مشاهده شده در ۱۰ بار پرتاب یک سکه باشد که شانس مشاهده شیر در آن برابر با p‌ است. در نتیجه تابع درست نمایی باید به صورت تابعی از پارامتر توزیع که همان p است، نوشته شود. بوسیله مقدار مشاهده شده از نمونه تصادفی، تابع درست نمایی برای این توزیع را به صورت زیر محاسبه می‌کنیم.

$$\large L(p)=f_{X_1,X_2,\ldots,X_n}(x_1,x_2,\ldots,x_n)=\prod_{i=1}^n f_{X}(x_i)=\prod_{i=1}^n {10 \choose x_i}p^{x_i}(1-p)^{10-x_i}$$

که می‌تواند به صورت ساده‌تر نوشته شود:

$$\large L(p)=p^{\sum x_i}(1-p)^{10\times n- \sum x_i}\prod_{i=1}^n {10 \choose x_i}$$

همچنین اگر فرض کنیم که تعداد شیرهای مشاهده شده در این n نمونه تصادفی همگی یکسان و برابر با 5 باشند، باز هم فرم ساده‌تری برای نمایش تابع درست نمایی توریع دو جمله‌ای ایجاد خواهد شد:

$$\large L(p)=p^{n\times 5}(1-p)^{50-n\times 5}{10 \choose 5}^n$$

در ضمن اگر تعداد نمونه تصادفی (n) از قبل مشخص شده باشد (مثلا n=5)، تابع درست نمایی به فرم زیر در خواهد آمد. مشخص است که با این کار تنها p به عنوان پارامتر تابع درست نمایی خواهد بود.

$$\large L(p)=p^{25}(1-p)^{25}{252}^{5}=p^{25}(1-p)^{25}\times 252^5$$

به این ترتیب، نمودار تابع درست نمایی به ازاء مقدارهای مختلف p‌ به صورت زیر درخواهد آمد.

برآورد پارامتر توسط تابع درست نمایی

معمولا با توجه به نمونه تصادفی، مقداری از فضای پارامتر که تابع درست نمایی را بیشینه کند، به عنوان برآورد درست نمایی پارامتر توزیع در نظر گرفته می‌شود. همانطور که در نمودار قبل دیده شد، با توجه به منحنی، حداکثر تابع در نقطه 0.5 بدست آمده است، پس با این روش، می‌توان برآورد درست نمایی توزیع دو جمله‌ای مثال قبل را با توجه به نمونه تصادفی بدست آمده، p=0.5 در نظر گرفت.

فیلم آموزش مقدماتی نظریه قابلیت اعتماد در فرادرس

کلیک کنید

مثال ۲

فرض کنید یک نمونه ۵ تایی از توزیع پواسن با پارامتر $$\lambda$$ گرفته‌ایم. پس داریم $$X_i\sim P(\lambda)$$. مقدار مشاهده شده برای این نمونه برابر است با $$x_1=2,x_2=3,x_3=4,x_4=2,x_5=4$$. شکل تابع درست نمایی و برآورد پارامتر $$\lambda$$ به صورت زیر خواهد بود:

$$\large L(\lambda)=\prod_{i=1}^5 P(X_i=x_i)=\prod_{i=1}^5\dfrac{\lambda^{x_i}e^{-\lambda}}{x_i!}=\dfrac{\lambda^{\sum x_i}e^{-n\lambda}}{x_1!x_2!\ldots x_5!}$$

با توجه به مقدارهای مشاهده شده از نمونه تصادفی ($$x_1=2,x_2=3,x_3=4,x_4=2,x_5=4$$) رابطه بالا را به صورت ساده‌تر زیر می‌نویسیم.

$$\large L(\lambda)=\dfrac{\lambda^{2+3+4+2+3}e^{-5\lambda}}{21!3!4!2!3!}= \dfrac{\lambda^{15}e^{-5\lambda}}{x_1!x_2!\ldots x_5!}$$

نمودار تابع درست نمایی برای این توزیع به شکل زیر درخواهد آمد.

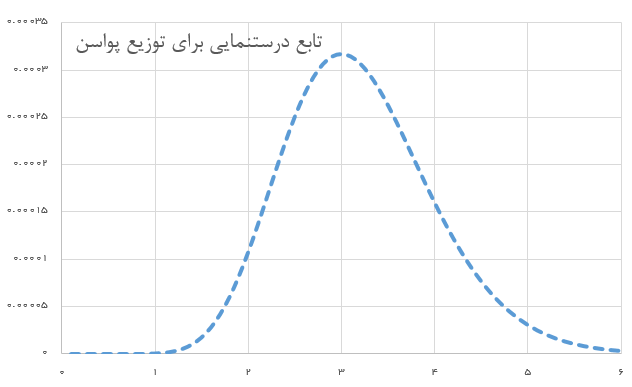
در نمودار ترسیم شده، مشخص است که به ازای $$\lambda=3$$، تابع درست نمایی حداکثر خود را خواهد داشت. همانطور که دیده می‌شود، میانگین مقدارهای نمونه تصادفی نیز برابر با ۳ است. در نتیجه به نظر می‌رسد که برآورد درست نمایی برای پارامتر چنین توزیعی همان میانگین مقدار مشاهده شده از نمونه‌ها باشد. ولی به کمک مشتق‌گیری و محاسبه مقدار بیشینه تابع درست نمایی نیز می‌توان به همین جواب رسید.

نکته: از آنجایی که هدف پیدا کردن بیشینه تابع درست نمایی است، گاهی می‌توان از لگاریتم تابع درست نمایی جهت بیشینه‌سازی استفاده کرد زیرا لگاریتم یک تابع یکنوا است. مشخص است که لگاریتم تابع درست نمایی درست در همان نقطه‌ای بیشینه می‌شود که تابع درست نمایی بیشینه خود را بدست می‌آورد.

با توجه به این موضوع، در مثال ۲ برآورد پارامتر توزیع پواسن را با طی کردن مراحل زیر انجام می‌دهیم. در اینجا فرض بر این است که تعداد نمونه تصادفی برابر با n و مقدارهایشان (مقدارهای حاصل از مشاهده) نیز برابر با $$x_1,x_2,\ldots,x_n$$ باشد.

1. محاسبه لگاریتم تابع درست نمایی
2. مشتق‌گیری از حاصل مرحله ۱ برحسب پارامتر ($$\lambda$$)
3. پیدا کردن ریشه حاصل از معادله مرحله ۲ (نقطه اکستریمم)
4. مشخص کردن نقطه بیشینه برای تابع درست نمایی

این مراحل در ادامه انجام شده است. همانطور که دیده می‌شود، حداکثر تابع درست نمایی (لگاریتم تابع درست نمایی) در نقطه‌ای که برابر با میانگین نمونه تصادفی است بدست می‌آید.

$$\large L(\lambda)=\prod_{i=1}^n P(X_i=x_i)=\prod_{i=1}^n\dfrac{\lambda^{x_i}e^{-\lambda}}{x_i!}=\dfrac{\lambda^{\sum x_i}e^{-n\lambda}}{x_1!x_2!\ldots x_n!}$$

$$\large ln(L(\lambda))=l(\lambda)=ln(\dfrac{\lambda^{\sum x_i}e^{-n\lambda}}{x_1!x_2!\ldots x_n!})= \sum_{i=1}^n x_i ln(\lambda)-n(\lambda)-ln(x_1!x_2!\ldots x_n!)$$

حال از مشتق لگاریتم تابع درست نمایی نسبت به $$\lambda$$ استفاده می‌کنیم.

$$\large \dfrac{\partial ln(L(\lambda))}{\partial \lambda}=\dfrac{\sum_{i=1}^n x_i}{\lambda}-n$$

این مشتق را برابر با صفر قرار داده و ریشه معادله حاصل را می‌یابیم.

$$\large \dfrac{\partial ln(L(\lambda))}{\partial \lambda}=0 \rightarrow \dfrac{\sum_{i=1}^n x_i}{\lambda}-n=0$$

$$\large \dfrac{\sum_{i=1}^n x_i}{\lambda}=n\rightarrow \lambda =\dfrac{\sum_{i=1}^n x_i}{n}$$

به منظور مشخص کردن بیشینه یا کمینه بودن این نقطه نیز کافی است از مشتق دوم کمک بگیریم. از آنجایی که مشتق دوم یعنی $$-\frac{1}{\lambda^2}$$ نیز منفی است، بیشینه بودن جواب تعیین می‌شود.

نکته: برآورد حاصل از بیشینه‌سازی تابع درست نمایی (لگاریتم تابع درست نمایی) را «برآوردگر حداکثر درست نمایی» (Maximum Likelihood Estimator) می‌نامند که بیشتر به برآوردگر MLE شهرت دارد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها
• توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی و توزیع پواسن — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^