تحلیل داده ها با استفاده از مقدار میانگین – به زبان ساده
مقدار میانگین یا میانگین عبارت سادهای با معانی مختلف است. نوع میانگینی که ما استفاده میکنیم به این بستگی دارد که مشغول جمع، ضرب، گروهبندی یا تقسیم آیتمهای یک مجموعه باشیم.


برای مثال اگر با سرعت 30 کیلومتر بر ساعت به سمت محل کار خود رانندگی کرده و با سرعت 60 کیلومتر بر ساعت از آنجا بازگردید، میانگین سرعت شما چه قدر بوده است؟
اگر فکر میکنید میانگین سرعت 45 کیلومتر بر ساعت بوده است، اشتباه میکنید و این مقدار به مسافتی به طی شده است نیز ارتباطی ندارد. در این مورد در ادامه بیشتر توصیه خواهیم داد فعلاً به این فکر کنید که چرا 45 پاسخ نادرستی محسوب میشود. در جدول زیر کاربردهای مختلف این ابزار آماری را مشاهده میکنید.
| نام و معنا | فرمول/ مثال | کاربرد |
|---|---|---|
| میانگین حسابی (معدل) | در اغلب موقعیتها به عنوان میانگین استفاده میشود. | |
| میانه (مقدار میانی) | عنصر میانه یک فهرست مرتب (اگر دو عنصر باشند میانگین آنها محاسبه میشود). | در مورد نمونههای با تغییرات زیاد مانند بهای خانهها یا درآمدها استفاده میشود. |
| مد (فراوانترین) | فراوانترین مقدار در مجموعه | هیچ سازشی در کار نیست و برنده همه عناصر را برمیدارد. |
| میانگین هندسی (عامل میانگین) | سرمایهگذاریها، رشد، مساحت، حجم | |
| میانگین هارمونیک (نرخ میانگین) | سرعت، تولید، هزینه |
معنی میانگین چیست؟
برای اغلب ما میانگین به معنی عدد وسط یا عدد متعادل است. اگر بخواهیم از منظری متفاوت به میانگین نگاه کنیم:
میانگین مقداری است که میتواند جایگزین هر آیتم موجود شود و نتیجه مشابهی ارائه کند. اگر همه دادهها را کنار گذاشته و تنها یک مقدار میانگین داشته باشیم به چه معنا خواهد بود؟
هدف ما از میانگین درک یک مجموعه داده با داشتن یک نمونه گویا از آن است. اما این محاسبه به شیوه تعامل آیتمها با هم در گروه وابسته است. در ادامه بیشتر توضیح میدهیم.
میانگین حسابی
میانگین حسابی رایجترین نوع میانگین است که از تقسیم مجموع عناصر بر تعداد آنها به دست میآید.
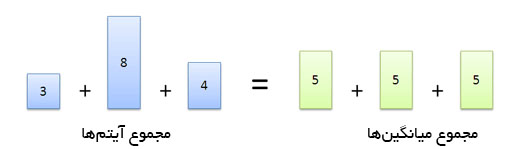
فرض کنید وزن شما 75 کیلوگرم است و در آسانسوری قرار دارید که در آن یک کودک 50 کیلویی و یک وال 175 کیلویی هستند. میانگین وزن چه قدر است؟
درواقع سؤال اصلی چنین است که اگر بخواهیم این گروه متضاد را با 3 فرد مشابه و با وزن یکسان در آسانسور قرار دهیم، وزن هر یک از این افراد چه قدر باید باشد؟
در این مورد اگر مجموع وزن اینها را بر تعداد آنها که 3 است تقسیم کنیم، به عدد 150 کیلوگرم میرسیم.
مزایا
- این نوع میانگین برای فهرستهایی مناسب است که به سادگی از طریق جمع قابل ترکیب باشند.
- محاسبه آن آسان است: کافی است جمع و تقسیم کنیم.
- درک آن آسان است زیرا عدد میانی بین مقادیر بالاتر و مقادیر کوچکتر قرار میگیرد.
معایب
- ممکن است مقدار میانگین به دلیل وجود مقادیر پرت دچار انحراف شود. در واقع این نوع میانگین در نمونههای با تغییرات شدید مناسب نیست. میانگین 75، 175 و -250 برابر با صفر است که گمراهکننده محسوب میشود.
- میانگین حسابی در 80 درصد موارد به خوبی عمل میکند. بسیاری از کمیتها با هم قابل جمع هستند. متأسفانه همواره 20 درصد از موارد هستند که میانگین چندان معنیدار نیست.
میانه
میانه به معنی عنصر میانی یک مجموعه است. اما از طرفی نباید آن را با میانگین (میانگین حسابی) اشتباه گرفت. برای مثال به نظر شما میانه اعداد زیر کدام است؟
1، 2، 3، 4، 100
بر اساس تعریف میدانیم که میانه فهرست فوق 3 است و با این که مقدار میانگین 22 در حقیقت در میانه فهرست فوق قرار دارد؛ اما در عمل نشاندهنده توزیع اعداد نیست. ما انتظار داریم که عددی بسیار نزدیک به 3 به دست بیاوریم تا این که عددی مانند 22 داشته باشیم. در واقع میانگین بر اساس 100 که یک مقدار پرت است، دچار انحراف شده است.
میانه این مشکل را با انتخاب عددی که در میانه یک فهرست مرتب قرار دارد حل میکند. اگر دو عدد در میانه فهرست مرتب وجود داشته باشد، یعنی تعداد کل اعداد زوج باشد، میتوانیم از این دو عدد میانگین گرفته و میانه را تعیین کنیم. اعداد پرتی مانند 100 نمیتوانند تأثیر زیادی روی میانه داشته باشند، زیرا میانه را تنها یک عدد به سمت چپ یا راست میبرند و تغییر قابل توجهی در میانه ایجاد نمیشود. به عنوان نمونه، میانه فهرست 1، 2، 3، 4 برابر با 2.5 است.

مزایا
- موارد پرت را به خوبی مدیریت میکند و در اغلب موارد بازنمایی دقیقی از گروه ارائه میدهد.
- دادهها را به دو گرو افراز میکند که هر یک تعداد یکسانی از اعضا دارند.
معایب
- محاسبه آن میتواند دشوارتر باشد، چون ابتدا باید فهرست مرتبسازی شود.
- چندان مشهور نیست و وقتی از میانه صحبت میکنیم، اغلب افراد فکر میکنند منظورمان میانگین است.
جوکهایی وجود دارند که برای مثال عنوان میکنند «نیمی از رانندگان وضعیت رانندگی زیر میانگین دارند»، که میخواهند کسانی که آمار نمیدانند را دست بیندازند؛ در حالی که خود این جوک، شامل یک اشتباه است، چون باید گفته شود «نیمی از رانندگان وضعیت رانندگی زیر میانه دارند»!
اعداد و ارقام قیمت مسکن و درآمدها عموماً بر حسب میانه بیان میشود، چون میخواهیم ایدهای از عنصر میانی یک دسته داشته باشیم. برای مثال چند میلیارد دلار درآمد اضافی که بیل گیتس در طی یک سال کسب میکند، میتواند میانگین درآمد کشور را به مقدار قابل توجهی بالا ببرد؛ ولی شاید این میانگین نتواند میزان تغییرات دستمزد یک کارگر معمولی را در طی آن سال به خوبی نشان دهد. به همین دلیل ایده جمع کردن قیمت مسکن یا درآمد افراد ایده خوبی محسوب نمیشود و در این موارد بهتر است صرفاً عنصر میانی یعنی میانه گروه را یافت.
در این مورد نیز نوع میانه به شیوه استفاده از دادهها وابسته است.
مُد
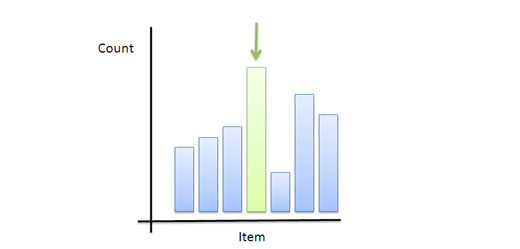
مفهوم مد تا حدودی عجیب است، اما شبیه به مفهوم رأیگیری است و در برخی موارد نیز واقعاً یک رأیگیری و نه محاسبه، بهترین روش برای دریافت نمونه گویایی از یک جمعیت است.
فرض کنید میخواهید جشنی برگزار کنید و به دنبال انتخاب یک روز هستید، روزهای هفته را از شنبه با عدد 1 تا جمعه با عدد 7 شمارهگذاری میکنید. بهترین روز آن روزی است که بیشترین افراد از آن راضی هستند. به طور مشابه ترجیحهای رنگ، فیلم و موارد دیگر میتوانند به وسیله اعداد اندازهگیری شوند. اما در این مورد نیز گزینه ایدهآل میتواند مد باشد؛ و نه میانگین، چون رنگِ میانگین یا میانگینِ فیلم ممکن است معنای چندانی نداشته باشد.
مزایا
- در مورد همه موقعیتهای رأیدهی انحصاری عمل میکند (انتخاب این یا آن؛ عدم مصالحه).
- گزینهای ارائه میکند که اغلب افراد میخواهند (در حالی که میانگین ممکن است گزینهای باشد که هیچ کس نمیخواهد).
- درک آن آسان است.
معایب
- محاسبه آن به تلاش بیشتری نیاز دارد.
- برنده همه چیز را میبرد و مسیر میانی وجود ندارد.
اصطلاح مد چندان رایج نیست؛ اما اینک دست کم زمانی که مشغول کار با برنامه آماری محبوب خود هستید، میدانید که باید از کدام دکمه برای محاسبه مد استفاده کنید.
میانگین هندسی
آیتم میانگین به چگونگی استفاده از عناصر موجودمان بستگی دارد. در اغلب موارد آیتمها با هم جمع میشوند و میانگین حسابی به خوبی کار میکند. اما در برخی موارد به کار بیشتری نیاز داریم. زمانی که با سرمایهگذاریها، و یا محیط و مساحت سر و کار داریم، عوامل مختلف را با هم جمع نمیکنیم؛ بلکه در هم ضرب میکنیم.
برای مثال به سودهای سالانهای که یک پورتفولیوی سهام ارائه کرده است توجه کنید. بررسی کنید که کدام پورتفولیوی زیر را ترجیح میدهید، یعنی کدام یک سود سالانه بهتری ارائه میکند؟
پورتفولیوی اول:
+10%, -10%, +10%, -10%
پورتفولیوی دوم:
+30%, -30%, +30%, -30%
این دو کاملاً شبیه به هم به نظر میرسند. میانگین هر روزه ما (میانگین حسابی) به ما میگوید که هر دو نوسان مختلفی دارند؛ اما میانگین سود یا زیان هر دوی آنها برابر با صفر است. احتمالاً B بهتر است، زیرا به نظر میرسد در سالهای خوب،، سود بالایی وجود داشته است؛ اما این گزاره نادرستی است. چنین تفکراتی در بازار سرمایه مانند سم است چون بازدهیهای سرمایه در هم ضرب میشود و جمع نمیشود! معنی این حرف آن است که نمیتوان به سادگی برج-خرج کرد و باید نرخ واقعی بازدهی را محاسبه نمود:
پورتفولیوی اول:
- بازدهی: (2% ضرر)
- میانگین سال به سال: ضرر در هر سال (این مقدار معادل است چون مقادیر کوچک هستند)
پورتفولیوی دوم:
- بازدهی: ضرر
- میانگین سال به سال: ضرر در هر سال
تفاوت بین ضرر 2 درصدی و 17 درصدی بسیار بزرگ است! در واقع از هر دو پورتفولیو باید اجتناب کرد؛ اما در صورت مجبور بودن، پورتفولیوی A بسیار بهتر است. بازدهیها را نمیتوان به سادگی جمع و تفریق کرد، چون رشد نمایی به این ترتیب عمل نمیکند.
برخی نمونههای دیگر:
- نرخهای تورم: اگر سه نرخ تورم 1، 2 و 10 درصد را در طی یک سال داشته باشیم، میانگین نرخ تورم در طی آن سال به صورت است.
- کوپنها: فرض کنید کوپنهای تخفیف به میزان 50%، 25% و 35% درصد دارید. با فرض این که بتوانید از همه آنها استفاده کنید، میانگین تخفیف چقدر خواهد بود؟ یعنی کدام کوپن است که 3 بار استفاده از آن معادل این کوپنها خواهد بود؟ . البته ما کوپنها را صورت منفی (از دید فروشگاه) در نظر گرفتیم.
- مساحت: فرض کنید نموداری از یک زمین به مساحت 40 در 60 متر دارید. ضلع آن به طور میانگین چقدر است؟ یعنی مربعی که متناظر این زمین باشد دارای چه اندازه ضلعی خواهد بود؟ متر.
- حجم: فرض کنید یک سبد خرید به ابعاد 48× 24 ×12 سانتیمتر دارید. اندازه میانگین آن چه قدر است؟ یعنی مکعب متناظر این ابعاد چه اندازهای خواهد داشت؟ سانتیمتر.
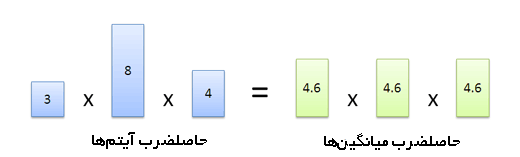
مطمئناً میتوان مثالهای بسیار زیاد دیگری را نیز یافت. میانگین هندسی «عنصر معمول» را در مواردی که آیتمها در هم ضرب میشوند مییابد. یک مجموعه از اعداد را انتخاب میکنیم و سپس آنها را در هم ضرب کرده و ریشه N-ام را محاسبه میکنیم (N تعداد آیتمهای مورد نظر است).
میانگین هارمونیک (همساز)
بصریسازی میانگین هارمونیک دشوارتر است؛ اما همچنان مفید است. در هر حال منظور از هارمونیک اعدادی مانند 2/1، 3/1 و اصولاً 1 روی هر چیزی است. میانگین هارمونیک به محاسبه نرخهای میانگین در زمانی که چند آیتم با هم کار میکنند کمک میکند. در ادامه این موضوع را بیشتر بررسی میکنیم.
اگر نرخ سرعت ما 30 کیلومتر بر ساعت باشد، به این معنی است که به ازای هر واحد از ورودی (1 ساعت رانندگی) نتیجه مشخصی (30 کیلومتر طی مسیر) به دست میآوریم. زمانی که از تأثیر نرخهای چندگانه (X و Y) میانگین میگیریم، باید در مورد خروجیها و ورودیها تأمل کنیم و نه اعداد خام.
ورودی کل / خروجی کل = نرخ میانگین

اگر هر دوی X و Y روی یک پروژه کار کنند و هر یک مقدار معینی از کار را انجام دهند، نرخ میانگین چه قدر خواهد بود؟ فرض کنید X با نرخ 30 کیلومتر بر ساعت و Y با نرخ 60 کیلومتر بر ساعت حرکت کنند. اگر از آنها بخواهیم کارهای مشابهی انجام دهند (یک کیلومتر رانندگی)، وضعیت به منوال زیر خواهد بود:
- X به مدت زمان کار میکند (هر کیلومتر = 1/30 ساعت)
- Y به مدت زمان کار میکند (هر کیلومتر = 1/30 ساعت)
با ترکیب کردن ورودیها و خروجیها وضعیت زیر به دست میآید:
- خروجی کل: 2 کیلومتر (X و Y هر کدام 1 کیلومتر مشارکت داشتهاند.)
- ورودی کل: (هر یک مقدار متفاوتی از زمان را صرف کردهاند)
نرخ میانگین، خروجی/ورودی به صورت زیر است:
اگر 3 آیتم به صورت X، Y و Z داشتیم، نرخ میانگین به صورت زیر میبود:
داشتن چنین میانبری به جای محاسبههای جبری همواره باعث صرفهجویی در زمان میشود و حتی در مورد یافتن 5 نرخ میانگین نیز عملکرد مناسبی دارد. در مثالی که در ابتدای نوشته مطرح کردیم، میخواهیم بدانیم که اگر با سرعت 30 کیلومتر بر ساعت به سمت محل کار رانندگی کنیم و با سرعت 60 کیلومتر بر ساعت از آنجا باز کردیم، میانگین سرعت چقدر بوده است. بدین منظور از فرمول فوق استفاده میکنیم.
اما آیا لازم نیست بدانیم مسافت منزل تا محل کار چه مقدار بوده است؟ پاسخ منفی است، چون مهم نیست که چه مسافتی طی شده است؛ X و Y خروجی یکسانی دارند، یعنی مسافتی که با سرعت X طی میکنیم، برابر با مسافتی است که با سرعت Y طی شده است. سرعت میانگین مانند این است که 1 کیلومتر را با سرعت X و 1 کیلومتر را با سرعت Y طی کرده باشیم:
مشخص است که میانگین سرعت باید به سمت سرعت پایینتر منحرف شود (یعنی به 30 نزدیکتر از 60 باشد) زیرا ما مدت زمانی که با سرعت 30 طی کردهایم، دو برابر زمانی است که با سرعت 60 طی کردهایم. یعنی اولی 2 ساعت و دومی 1 ساعت طول کشیده است.
ایده مهم
میانگین هارمونیک زمانی استفاده میشود که دو نرخ مختلف در یک «بارِ کاری» (workload) مشترک مداخله داشته باشند. هر نرخ، میزان مشارکت یکسانی در کار انجام شده نهایی داشته است. برای نمونه در مثال فوق ما یک سفر به محل کار رفته و همان مسیر را بازگشتهایم. نیمی از نتیجه (مسافت پیموده شده) با نرخ اولیه (30 کیلومتر بر ساعت) و نیمی دیگر با نرخ دوم (60 کیلومتر بر ساعت) بوده است.
نکته مهم
به خاطر داشته باشید که میانگین عنصر منفردی است که جایگزین همه عناصر میشود. در مثال فوق ما با سرعت 40 کیلومتر بر ساعت کل مسیر را پیمودهایم و میتوانیم آن را جایگزین سرعتهای 30 (از منزل تا محل کار) و 60 کیلومتر بر ساعت (از محل کار تا منزل) بکنیم. باید به خاطر بسپارید که همه مراحل را میتوان با نرخ میانگین جایگزین کرد.
چند مثال دیگر
در این بخش برای درک بهتر مفهوم میانگین همساز چند مثال دیگر ارائه شده است:
مبادله داده
فرض کنید دادههایی را بین کلاینت و سرور انتقال میدهیم. کلاینت با نرخ 10 گیگابایت/هزار تومان دادهها را ارسال میکند و سرور با نرخ 20 گیگابایت/هزار تومان دادهها را دریافت میکند. میانگین هزینه این مبادله داده چه قدر است؟ میدانیم که میانگین نرخ هزینه مبادله برای هر بخش برابر با گیگابایت/هزار تومان است. از آنجا که دادهها دریافت و ارسال شدهاند (و هر بخش نیمی از کار را انجام داده است) نرخ واقعی برابر با 6.65 = 2 / 13.3 گیگابایت /هزار تومان خواهد بود.
بهرهوری دستگاه
تصور کنید دستگاهی داریم که اقدام به آمادهسازی و پرداختکاری یک قطعه خاص میکند. دستگاه در زمان آمادهسازی قطعه با نرخ 25 قطعه/ساعت کار میکند و زمان پرداختکاری، نرخ کاری آن به صورت 10 قطعه/ساعت است. نرخ کلی تولید قطعه چه قدر است؟ اگر میانگین دو بخش را محاسبه کنیم قطعه/ساعت برای هر بخش خواهد بود. یعنی زمانهای موجود را میتوان با زمان میانگین یکسان 14.28 قطعه/ساعت جایگزین کرد و نتیجه یکسان خواهد بود. از آنجا که تولید قطعه در دو فاز صورت میگیرد، دستگاه ما کار خود را با نرخ 7.14 = 2 / 14.28 قطعه / ساعت انجام میدهد.
خرید سهام
فرض کنید ماهانه سهامی به ارزش 1 میلیون تومان میخرید و برایتان مهم نیست که قیمت سهام چه قدر باشد. مثلاً در ماه فروردین 25 هزار تومان برای هر سهم پرداختهاید و در ماههای اردیبهشت و خرداد نیز به ترتیب 30 هزار تومان و 35 هزار تومان برای هر سهم پرداخته کردهاید. اینک سؤال این است که چه مقدار سهام دارید و میانگین قیمت هر سهم چه در بوده است؟ با استفاده از فرمول محاسبه میانگین هارمونیک میانگین قیمت سهمها برابر با بود i است. دلیل آن این است که سهم بیشتری را با قیمت پایینتر و مقدار کمتری را با قیمت بالاتر خریدهاید و اینک 101.94 = 29430/ 30000000 سهم دارید. در اینجا مفهوم بار کاری تا حدی پیچیدهتر است، چون مبالغ به صورت سهام درمیآیند. برخی ماهها مبالغ پایینتری برای خرید سهام صرف شده و برخی دیگر ماهها بالاتر بوده و در این مورد نرخ بالاتر معنی منفی دارد.
در این مورد نیز باید گفت که میانگین هارمونیک به اندازهگیری نرخهایی کمک میکند که با همکاری هم نتیجه یکسانی تولید میکنند.
معما چو حل گشت آسان شود
میانگین هارمونیک پیچیده است، چون اگر دستگاههای مجزایی باشند که با نرخ تولید 10 قطعه/ساعت و 20 قطعه/ساعت کار کنند، در این صورت نرخ واقعی میانگین تولید آن دو دستگاه مجزا برابر با 15 قطعه/ساعت خواهد بود، چرا که دستگاهها مستقل از هم کار میکنند و ظرفیتها با هم جمع میشوند. در این حالت میانگین حسابی به خوبی جواب میدهد.
برخی اوقات بهتر است موارد مختلف را مجدداً بررسی کنیم تا مطمئن شویم که فرمولهای صحیحی را استفاده میکنیم. در مثال دستگاه تولید قطعه ادعا کردیم که 7.14 قطعه بر ساعت تولید میکنیم. این درست است؛ اما چه زمانی طول میکشد تا بتوانیم 7.14 قطعه تولید کنیم؟
- آمادهسازی: 0.29 = 25/7.14 ساعت
- پرداخت: 0.71 = 10 / 7.14 ساعت
اینک میبینیم که با جمع زدن اعداد 0.29 و 0.71 به عدد 1 میرسیم که همان 1 ساعت مورد نظر است. یعنی 1 ساعت برای تولید 7.14 قطعه مورد نیاز است و این محاسبه صحیح است. با بررسی چند مثال سعی کنید مطمئن شوید که نرخ میانگینی که محاسبه کردهاید صحیح بوده است.
سخن پایانی
حتی ایده سادهای مانند میانگین نیز کاربردهای زیادی دارد. موارد زیادی وجود دارند که در این نوشته بررسی نکردیم و از آن جمله نقطه ثقل، میانگینهای وزندار، امید ریاضی و غیره. نکته کلیدی چنین است:
- آیتم میانگین را میتوان به عنوان آیتمی در نظر گرفت که میتواند جایگزین همه آیتمهای دیگر شود.
- نوع میانگین به شیوه استفاده از آیتمهای موجود بستگی دارد (جمع میشوند، ضرب میشوند، به عنوان نرخ استفاده میشوند، یا گزینههای انحصاری هستند.)
انواع مختلف میانگین برای تحلیل دادههای مختلف بسیار مفید هستند.
اگر این نوشته برای شما مفید بوده است، پیشنهاد ما استفاده از آموزشهای زیر است:
- مجموعه آموزشهای ریاضیات
- مقایسه معیارهای تمرکز (میانگین، میانه، نما)
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- رابطه بین میانگین حسابی، هندسی و همساز
- انحراف میانگین — به زبان ساده
- میانگین وزنی — به زبان ساده
- میانگین همساز — به زبان ساده
- روش یافتن میانگین – به زبان ساده
==













با سلام و احترام
اگر 31 داده داشته باشیم که از کم به زیاد ردیف کرده و یک خط منحنی با شیب ملایم رو به بالا داشته باشد. حال بخواهیم به تمام اون 31 داده ضریب رشدی بدهیم که داده های کوچکتر ضریب بیشتر و داده های بزرگتر ضریب کمتری بگیرند و کلا به طور میانگین کل 31 داده 30 درصد رشد داشته باشد از چه منطقی باید استفاده کرد؟
خیییلی ممنونم استاد
شما انسان بسیار شریف و لایقی هستید?
سلام
توضیحات عالی هست ولی یه سوال دارم
اگه مقداری از جنسی رو در یه قیمت و بعد مقداری کمتر در یه قیمت دیگه و بعد مقداری دیگه در یه قیمت دیگه خریده باشیم
چطوری میتونیم محاسبه کنیم اون جنس در کل چند آب خورده برامون؟
سلام و وقت بخیر؛
مقدار جنسی که در قیمت اول خریدید را در این قیمت ضرب کنید، مقدار دوم را در قیمت دوم و همین طور تا آخر و در انتها همه این موارد را با هم جمع کرده و تقسیم بر تعداد کل بکنید. برای مثال اگر ده کیلوگرم با قیمت 900 تومان، دو کیلوگرم با قیمت 3500 تومان و پنج کیلوگرم با قیمت 7000 تومان خریداری شده باشد، میانگین همه این مقادیر برابر با 3000 تومان است که به صورت زیر محاسبه میشود:
17(10×900)+(2×3500)+(5×7000)=1751000=3000
از توجه شما متشکریم.