نسبت طلایی – به زبان ساده


نسبت طلایی عددی ثابت، برابر با ....۱.۶۱۸ است. این عدد در بسیاری از فعالیتهای هنری و مهندسی مورد استفاده قرار میگیرد.
ایده شکلگیری این نسبت
جهت بدست آوردن نسبت طلایی، خطی به طول L را در نظر بگیرید.
خط مفروض را مطابق با شکل زیر به دو بخش a و b تقسیم کنید.
a و b را به صورتی انتخاب میکنیم که رابطه زیر بین آنها برقرار باشد.
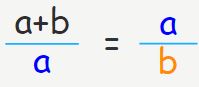
در این صورت حاصل این نسبتها برابر با عدد طلایی است. به شکلی ریاضیاتی میتوان گفت:
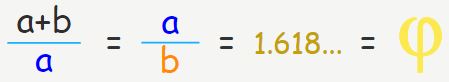
زیبایی
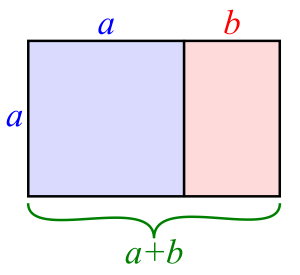
نکتهای بسیار جالب در مورد نسبت طلایی این است که زیبایی و چشم نوازی بسیاری از طراحیهای فیگور انسان و اشیای دیگر با این عدد در ارتباط است. در شکل زیر مستطیل طلایی نشان داده شده است. در حقیقت نسبت طول به عرض این مستطیل برابر با نسبت طلایی است.
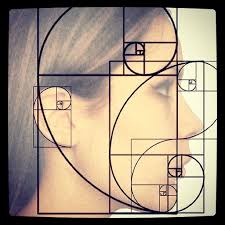
جالب است بدانید اگر مطابق با شکل زیر قطرهای مستطیلهای طلایی تشکیل شدهی درون مستطیل اصلی را با استفاده از قوسی به هم وصل کنیم منحنی حلزونی شکل بدست میآید.

معمولا در ساخت ال سی دیها، مانیتورها، طراحی خودرو و در جاهایی که با اشکال هندسی در ارتباط هستند در حد امکان از نسبت طلایی استفاده میشود. برای نمونه در پرستشگاه باستانی «پارتنون» (Parthenon) در یونان از نسبت طلایی استفاده شده است. در آن زمان، سازندگان اطلاعی از این نسبت نداشتهاند و به نظر میرسد این نسبت به صورت غریزی و با توجه به زیبایی بصری انتخاب شده است.

توجه داشته باشید که مقدار واقعی این نسبت برابر است با:

روش محاسبه
شما میتوانید این عدد را با استفاده از قدمهای زیر بدست آورید.
- عددی را در نظر بگیرید.
- ۱ را به عدد فرض شده تقسیم کنید. (عدد فرض شده/۱)
- کل عدد بدست آمده در مرحله قبل را با ۱ جمع کنید.
- عدد بدست آمده در مرحله ۳ را به عنوان عددی جدید در نظر بگیرید و دوباره همین مراحل را چندین بار تکرار کنید.
با انجام قدمهای شرح داده شده در بالا برای چندین بار، به عدد طلایی خواهید رسید. در جدول زیر با فرض اینکه عدد اولیه برابر با ۲ باشد، این مراحل انجام شده است.
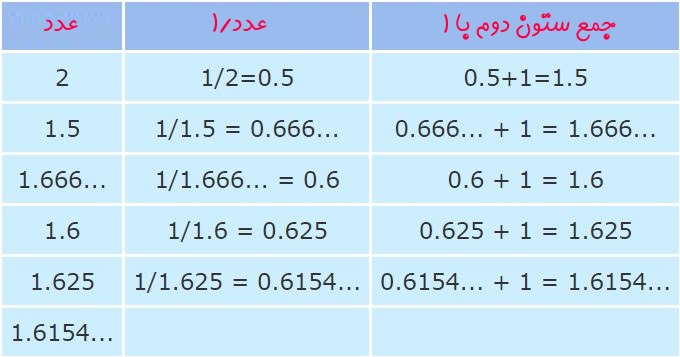
البته این عدد را میتوان به روشهای دیگری نیز یافت؛ از این رو در ادامه مقدار دقیق آن را در قالب یک فرمول مشخص ارائه خواهیم کرد. جهت بدست آوردن مقدار دقیق نسبت طلایی بهتر است در ابتدا همانند طراحان یونان باستان، مستطیلی را با این نسبت رسم کنیم و پس از آن با استفاده از طول اضلاع آن، نسبت طلایی را بدست آوریم.
رسم مستطیل طلایی
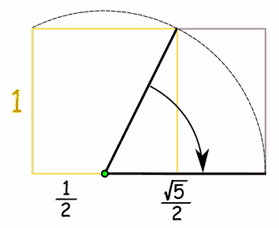
جهت رسم مستطیل طلایی در ابتدا مربعی با اضلاع واحد رسم کنید. سپس مطابق با شکل زیر وسط یکی از اضلاع آن را با استفاده از یک نقطه مشخص کنید و از آن خطی به سمت گوشه سمت راست بکشید. نهایتا با دوران خط مفروض به روی ضلع مربع اولیه، به گوشه مستطیل میرسیم. با رسم مستطیل حاصل از دو نقطه سمت چپ (گوشههای مربع اولیه) و نقطه بدست آمده، مستطیل طلایی بدست میآید.
به دست آوردن فرمول
با استفاده از قانون فیثاغورس طول خط دوران برابر با بدست میآید. در نتیجه طول مستطیل برابر با خواهد بود. عرض مستطیل نیز برابر با ۱ است. در نتیجه نسبت طول به عرض (یا همان نسبت طلایی) برابر است با:
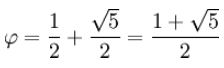
از نظر هندسی نیز میتوان ثابت کرد که حاصل (2sin(54۰ برابر با نسبت طلایی است.
ارتباط نسبت طلایی و سری فیبوناتچی
رابطه ویژهای میان سری فیبوناتچی (یا فیبوناچی) و نسبت طلایی وجود دارد. سری فیبوناتچی عبارت است از زنجیرهای از اعداد که هر عدد برابر با حاصل جمع دو عدد قبل از آن است. چند جمله اول این سری به صورت زیر است.
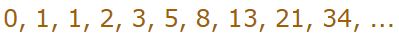
نکته جالب در سری فیبوناتچی این است که با تقسیم دو جمله متوالی از آن، عدد بدست آمده نزدیک به نسبت طلایی است. در پایین این عمل را برای چند جمله از این سری انجام دادهایم.
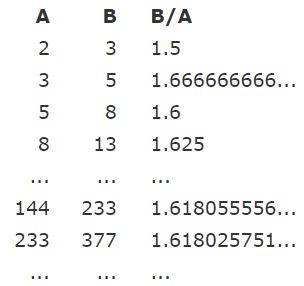
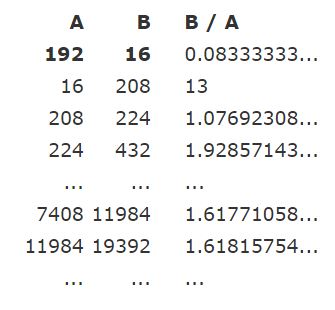
جالب است بدانید که حتی نیاز نیست اعداد اولیه انتخابی ما ۲ و ۳ باشند. برای نمونه در ادامه با فرض ۱۶ و ۱۹۲ به عنوان اعداد اولیه این نسبت محاسبه شده است.
گنگترین عدد
نسبت طلایی را میتوان یکی از گنگترین اعداد ثابتِ شناخته شده دانست. جهت بررسی گنگ و یا گویا بودن یک عدد بایستی آن را به شکل کسری نوشت. از طرفی نسبت طلایی را وابسته به خودش و به صورت زیر بیان کرد:
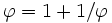
با جایگذاری φ در رابطه بالا، نسبت طلایی به شکل زیر قابل بیان میشود:
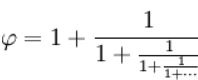
پنج ضلعی
پنج ضلعی را به عنوان نمادی اسرار آمیز میشناسند چراکه نسبت اضلاع موجود در آن برابر با نسبت طلایی است. پنج ضلعی زیر را در نظر بگیرید.
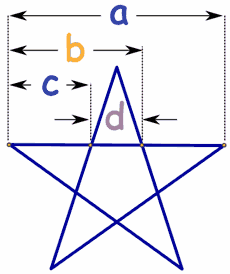
با توجه به بخشهای نشان داده شده در بالا، روابط زیر در آن برقرار است.














عالی است
زیبا بود لذت بردم
خوب بود ولی من در مورد تحقیق میخوام هرجا میرم فرمولو ایناشو داره
خوب بود ممنون
سلام
ببخشید ، شما با چه نرم افزاری فیلم های تان را ضبط می کنید؟
عالی
سلام من فکر میکنم که عددفی یاشکل به ریاضی ربت نداشته باشد شایدیک کلمه باشد .مثال برای کسی x مگوینداما فرد است.ببخشید خدا نگهدارشما
Such a wow!