برنامه محاسبه نقاط (x, y) با فاصله منهتن N – راهنمای کاربردی

در این مطلب، روش نوشتن برنامه محاسبه نقاط (x, y) با فاصله منهتن N بیان شده و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) ارائه شده است.

برنامه محاسبه نقاط (x, y) با فاصله منهتن N

عدد N داده شده است. هدف، پیدا کردن نقاط صحیح (x, y) به گونه‌ای است که $$0 <= x$$، $$y <= N$$ و فاصله منهتن بین دو نقطه، حداقل N باشد. مثال زیر در این رابطه، قابل توجه است.

Input: N = 3
Output: (0, 0) (0, 3) (3, 0) (3, 3)

Input: N = 4
Output: (0, 0) (0, 4) (4, 0) (4, 4) (2, 2)

در ادامه، رویکرد مورد استفاده برای پیدا کردن نقاط (x, y) با فاصله منهتن N بیان شده است.

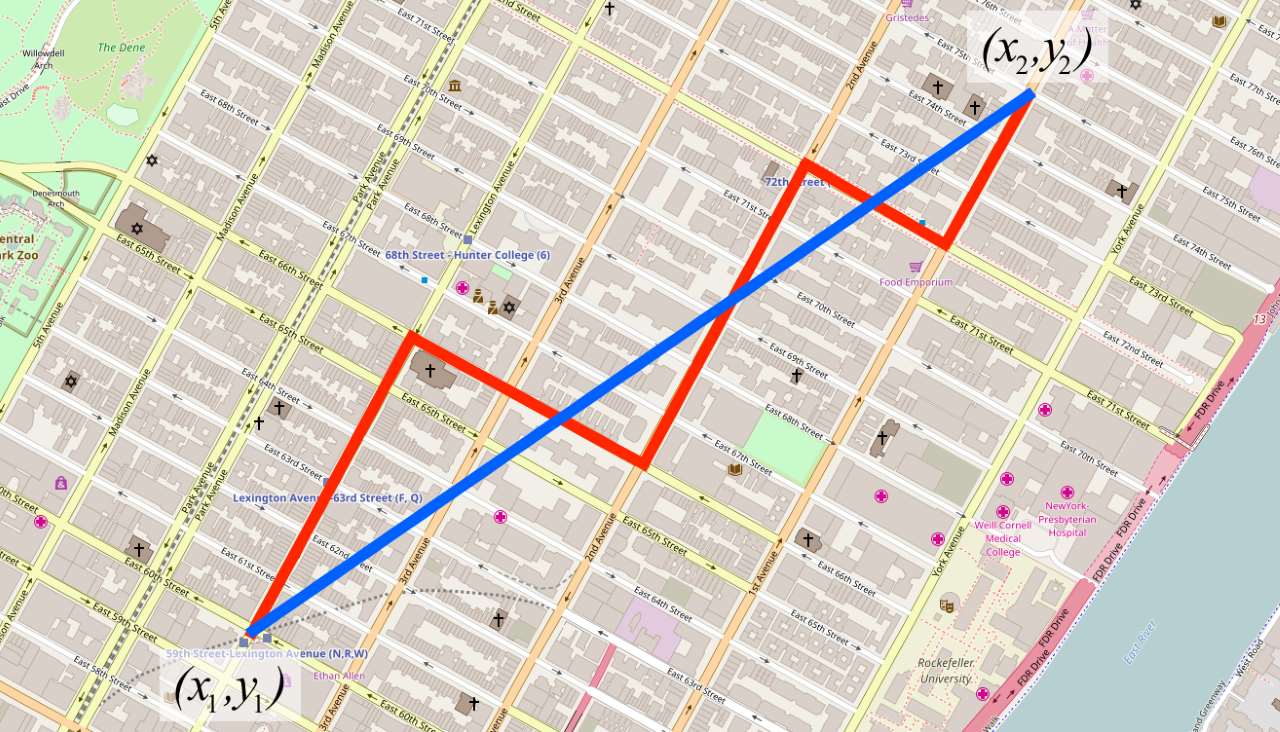
• فاصله منهتن بین دو نقطه (x₁, y₁) و (x₂, y₂) برابر است با $$|x_{1} – x_{2}| + |y_{1} – y_{2}|$$
• در اینجا، برای همه جفت نقاط، فاصله حداقل N است.
• با توجه به اینکه $$0 <= x <= N$$ و $$0 <= y <= N$$، می‌توان مربعی با طول N را تصور کرد که گوشه پایین و سمت چپ آن (0 ,0)‎ و گوشه بالا و سمت راست آن (N, N) است.
• اگر ۴ نقطه در این گوشه قرار بگیرد، فاصله منهتن حداقل N خواهد بود.
• اکنون، باید تعداد نقاطی که باید آن‌ها را بررسی کرد تا مشخص شود آیا نقطه‌ای درون مربع وجود دارد یا خیر، بیشینه شود.
• اگر N فرد باشد، نقطه میانی مربع که (N/2, N/2) است، یک نقطه صحیح است؛ در غیر این صورت، یک مقدار شناور همچون N/2 است که هنگامی که N فرد باشد، صحیح نیست.
• بنابراین، تنها موقعیت موجود، نقطه میانی است و می‌توان یک نقطه را در صورتی که N زوج باشد، در آنجا قرار داد.
• بنابراین، تعداد نقاط در صورتی ۴ است که N فرد باشد و اگر N زوج باشد، تعداد نقاط ۵ تا خواهد بود.

در ادامه، پیاده‌سازی روش بالا ارائه شده است.

برنامه محاسبه نقاط (x, y) با فاصله منهتن N در ++C

برنامه محاسبه نقاط (x, y) با فاصله منهتن N در جاوا

برنامه محاسبه نقاط (x, y) با فاصله منهتن N در پایتون

برنامه محاسبه نقاط (x, y) با فاصله منهتن N در #C

خروجی قطعه کدهای بالا برای N = 8، به صورت زیر است.

(0, 0) (0, 8) (8, 0) (8, 8) (4, 4)

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

^^