عدد اویلر یا نپر – به زبان ساده
فرمول اویلر، معرفی شده بعنوان زیباترین فرمول ریاضیات. چرا که شامل سه عمل اصلی جبر و سه نوع عدد غیر جبری در دنیاهای متفاوت بطور همزمان است. سه عمل اصلی شامل جمع، ضرب و توان و سه عدد غیر جبری شامل عدد اویلر، عدد پی و عدد موهومی (جذر عدد 1-). در این آموزش قصد داریم تا با عدد اویلر آشنا شویم.

عدد e (عدد اویلر) (عدد نپر) (Euler's Number) عدد گنگ معروفی است، و یکی از مهمترین اعداد در ریاضیات است.
این عدد تا چندین رقم اعشار در زیر نوشته شده است:
2.7182818284590452353602874713527...
|
بیشتر با نام عدد اویلر (Euler's Number) به افتخار لئونهارد اویلر شناخته می شود. دقت کنید که کلمه Euler "اویلر" خوانده می شود. |
e پایه لگاریتم طبیعی است (که توسط جان نپر اختراع شده)
e در بیشتر موضوعات ریاضی یافت می شود، پس یادگیری مفهوم آن ارزشش را دارد.
محاسبه مقدار عدد اویلر
روش های بسیاری برای محاسبه مقدار e وجود دارد، اما هیچکدام از این روش ها، عددی دقیق در اختیار نمی گذارند، چرا که عدد e عددی گنگ است (نسبتی از دو عدد صحیح نیست)
اما این عدد تا دقت 1 تریلیون شناخته شده است!
برای مثال، به عبارت زیر نگاهی بکنید:
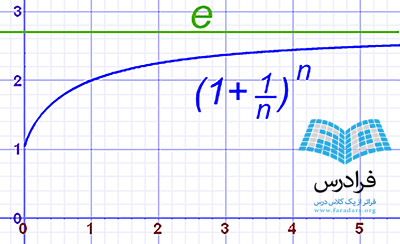
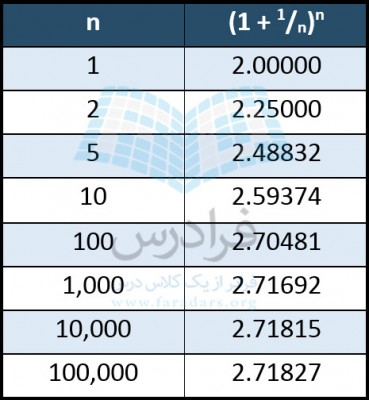
(1 + 1/n)n
مقدار این عبارت با افزایش n به عدد e نزدیک و نزدیک تر می شود:
روش محاسبه دیگر
مقدار e همچنین برابر جمع فاکتوریل ها به ترتیب زیر است:
1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + 1/7! + ...
جمع چند جمله اول به شکل زیر می شود:
1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 = 2.718055556
روشی برای حفظ کردن این عدد
اگر دقت کنید، بعد از رقم اول اعشار این عدد (بعد از 2.7)، چهار رقم 1828 دو بار تکرار می شود:
2.7 1828 1828
و بعد از آن سه عدد 45، 90 و 45 می آیند که زاویه ها را به خاطر می آورند (زاویه های یک مثلث قائم الزاویه متساوی الساقین):
2.7 1828 1828 45 90 45
(روشی فوری برای واقعا نابغه بنظر رسیدن!)
یک ویژگی جالب
بعنوان تفریح از روش "تقسیم و سپس ضرب" استفاده می کنیم
بهتر است بگوییم عددی را به تعدادی تقسیم می کنیم و سپس تمامی قسمت ها را به هم ضرب می کنیم.
مثال: عدد 20 را به 4 قسمت تقسیم کنید و سپس آنها را به هم ضرب کنید:
اندازه هر "قسمت" برابر 20/4 یا 5 است
5 × 5 × 5 × 5 = 54 = 625
اکنون،... چگونه می توانیم پاسخ را به بزرگترین اندازه ممکن بگیریم؟ اندازه هر قسمت باید چه مقدار باشد؟
مثال: این بار 5 قسمت را امتحان کنید
اندازه هر "قسمت" برابر 20/5 یا 4 است.
4 × 4 × 4 × 4 × 4 = 45 = 1024
بله! این جواب بزرگتر است! اما آیا بهترین اندازه ای داریم که از همه اندازه ها بزرگتر باشد؟
مثال: عدد 10
این بار عدد 10 را امتحان می کنیم:
عدد 10 در 3 قسمت می شود ...3.3
3.3... × 3.3... × 3.3... = (3.3...)3 = 37.037...
عدد 10 در 4 قسمت می شود 2.5
2.5 × 2.5 × 2.5 × 2.5 = 2.54 = 39.0625
عدد 10 در 5 قسمت می شود 2
2 × 2 × 2 × 2 × 2 = 25 = 32
برنده مقداریست که به عدد "e" نزدیک تر باشد، که در این مثال 2.5 از همه بیشتر به این عدد نزدیک بود.
این قضیه را با عددی دیگر امتحان کنید، مثلا 100... کدام عدد بیشتر از همه است؟
پیشرفته: استفاده از عدد اویلر در سود ترکیبی
عدد e اغلب در جاهایی ظاهر می شود که انتظار آن را نداریم.
برای مثال، e در ترکیب مستمر (برای وام ها و سرمایه گذاری ها) استفاده می شود:
![]()
فرمول برای ترکیب مستمر
چگونه عدد اویلر از این جا سر در آورده؟
خب... فرمول ترکیب دوره ای به شرح زیر است:
|
FV = PV (1 + r/n)n FV = مقدار آینده PV = مقدار کنونی r = میزان سود سالانه (به شکل عدد اعشاری) n = تعداد دوره ها |
اما اگر تعداد دوره ها به سمت بی نهایت برود چه اتفاقی می افتد؟
پاسخ در شباهت بین فرمول های زیر است:
(1 + r/n)n
فرمول ترکیب و
(1 + 1/n)n
فرمول عدد اویلر (با میل n به بی نهایت)
با تغییر متغیر x = n/r:
- r/n برابر معکوس x است.
- n برابر xr می شود.
و در نتیجه:
(1 + r/n)n
می شود
(1 + (1/x))xr
که دقیقا شبیه فرمول برای e (با رفتن n به سمت بی نهایت) است، اما با r بعنوان توان.
پس همین که x به سمت بی نهایت میل کند،
(1 + (1/x))xr
به سمت er میل می کند.
و این دلیل ظاهر شدن e در محاسبات است! عدد e همچنین عددی غیر جبری است.
آزمون عدد اویلر
۱. در مقایسه با فرمول تقریب ، کدام روش همگرایی سریعتری به سوی عدد اویلر (e) دارد و چرا؟
هر دو روش دقیقا همزمان به مقدار e نزدیک میشوند و تفاوتی ندارند.
فرمول سریعتر همگرا میشود زیرا افزایش n تاثیر زیادی دارد.
جمع سری معکوس فاکتوریلها سریعتر همگرا میشود چون با چند جمله ابتدایی عدد e تقریبا بهدست میآید.
هیچکدام بدون استفاده از کامپیوتر قابل تقریب نیستند و تفاوتی ندارند.
جمع سری معکوس فاکتوریلها به این دلیل سریعتر به عدد "e" نزدیک میشود که حتی با جمع کردن چند جمله اول آن، مقدار حاصل تقریب خوبی از عدد اویلر را نشان میدهد. در مقابل، فرمول نیاز به افزایش خیلی زیاد n دارد تا مقدارش به عدد e نزدیک شود و تجمع تقریب کندتر رخ میدهد.
۲. اگر عددی را به چند قسمت مساوی تقسیم کنیم تا حاصلضرب این قسمتها بیشینه شود، مقدار هر قسمت به چه عددی نزدیک خواهد شد؟
عدد پی
عدد اویلر
عدد طلایی
عدد نپرین طبیعی
مقدار هر قسمت زمانی که تقسیم بهینه انجام شود، به عدد اویلر که با نماد e هم شناخته میشود نزدیک خواهد بود. در تقسیم یک عدد به بخشهای مساوی جهت بیشینه کردن ضرب، بهترین نتیجه زمانی به دست میآید که هر قسمت ارزشی نزدیک به «عدد اویلر (e)» داشته باشد.












جالب نبود و مانند عدد نپر گنگ بود
سلام و سپاس
در آخر متن، در جمله “به سمت er میل می کند.” فکر میکنم r باید توان e باشد
فکنم جواب یک ویژگی جالب k/e هست نه عدد نزدیک نپر
سلام.
فرمول اصلاح شد.
سپاس از همراهی و بازخورد دقیقتان.
جایی از متن نوشتید عدد اویلر بیمعنیست! قاعدتاً باید ترجمهی irrational باشه.
در فارسی به این اعداد میگیم اصم، گنگ یا غیرگویا.
فقط میتونم بگم این زبان خداست
حتی برای اینکه بیشترین سود رو ببریم
سلام. متن اصلاح شد.
از همراهی و بازخوردتان سپاسگزاریم.
استفاده کردیم…تشکر
با سلام وتشکر-دررابطه:1+1/x^xr وقتی x بسمت بی نهایت میل کند جواب کسر 1برx=صفر می شود.ولذا 1 بتوان بی نهایت می شود همان 1 پس چگونه بسمت er میل کرده؟.ممنون
سلام.
آنچه در این مطلب نوشته شده صحیح است. در محاسبه حد، عبارت 1∞ مبهم است و برای محاسبه مقدار صحیح آن باید از روشهای دیگر کمک گرفت. برای آشنایی با این موضوع پیشنهاد میکنیم به آموزش «رفع ابهام حد — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
از همراهیتان با مجله فرادرس خوشحالیم.
سلام و سپاس. در اکسل اما با افزایش مقدار n به 1000000000000000 در فرمول، مقدار e به 3.035035207 می رسد. علتش چیست؟
اشتباه محاسباتی
سلام عدد اویلر به توان بی نهایت مساوی به چه می باشه؟
سلام خدمت شما دوست گرامی من نویسنده مطلب نیستم اما میدونم این عدد رو نمیشه نوشت ، فقط میشه به همان شکل خواند. چون بینهایت فقط یه مفهومه دوست عزیزhttps://blog.faradars.org/what-is-infinity/
سلام.بینهایت. چون بزرگتر از یک هست