تحلیل الاستو پلاستیک در سازه های معین و نامعین استاتیکی – به زبان ساده
در مبحث «رفتار غیر خطی مواد»، به بررسی رفتار سازهها پس از ناحیه الاستیک خطی پرداختیم. در این مقاله، با در نظر گرفتن منحنی تنش-کرنش یک ماده الاستو پلاستیک نظیر فولاد سازهای، شما را با مبانی تحلیل الاستو پلاستیک در سازههای معین و نامعین استاتیکی آشنا خواهیم کرد. از آنجایی که فولاد سازهای یا فولاد نرم، یکی از مواد پرکاربرد در ساخت سازههای فلزی به شمار میرود، تمرکز اصلی ما در این مقاله بر روی بررسی منحنی تنش-کرنش این ماده خواهد بود. در انتها نیز به منظور آشنایی با نحوه تحلیل سازههای الاستو پلاستیک، به تشریح یک مثال ساده خواهیم پرداخت.
منحنی تنش-کرنش الاستو پلاستیک
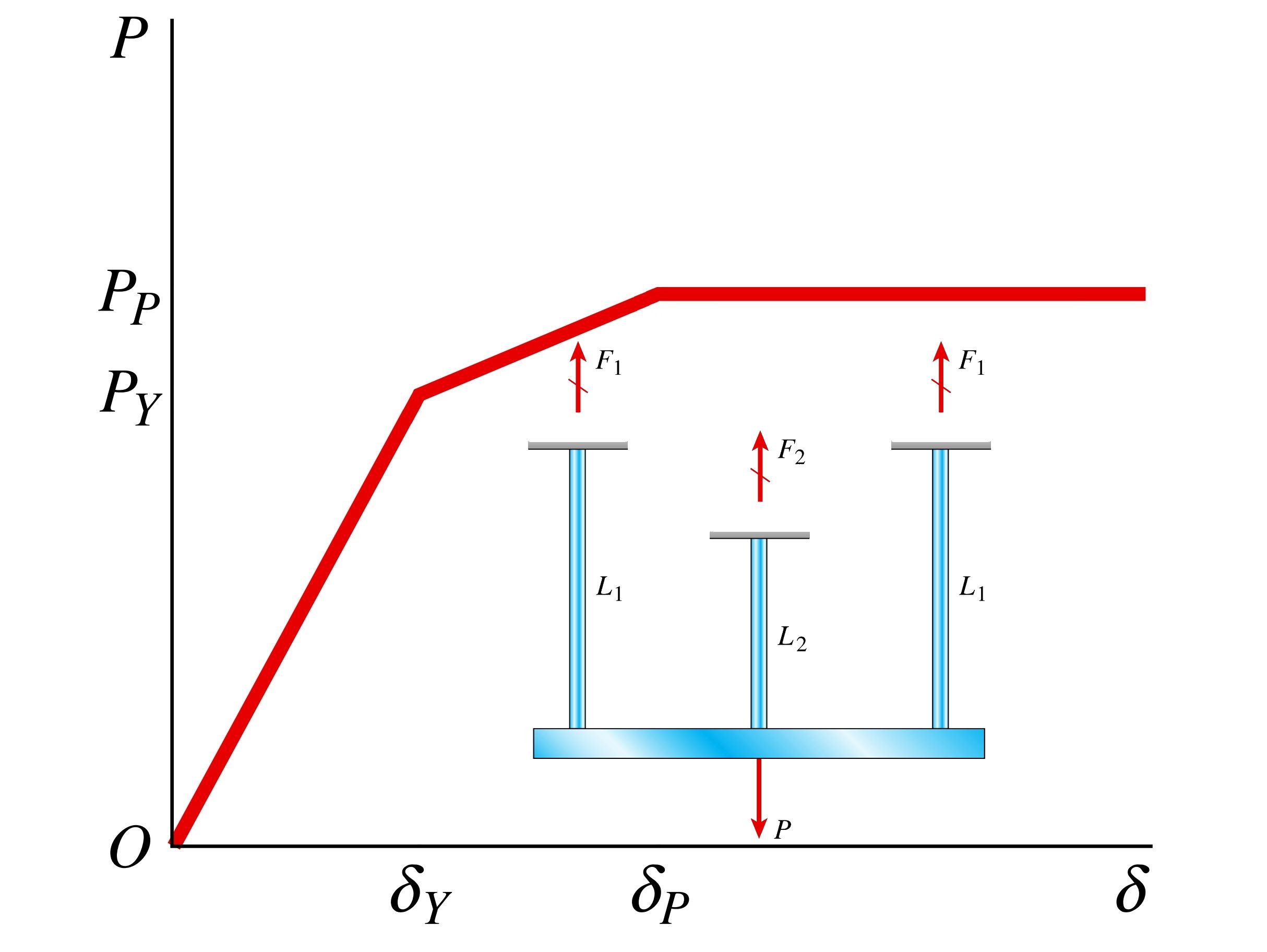
در شکل زیر، منحنی تنش-کرنش ایدهآل برای یک نوع فولاد سازهای نمایش داده شده است. همانگونه که مشاهده میشود، این فولاد در ابتدا به صورت الاستیک خطی رفتار میکند. پس از شروع تسلیم پلاستیک و در محدودهای با تنش تقریباً ثابت، میزان کرنش افزایش مییابد.
این تنش با عنوان «تنش تسلیم» (Yield Stress) شناخته میشود (σY). کرنش ایجاد شده در شروع تسلیم، «کرنش تسلیم» (Yield Strain) نام دارد (εY).
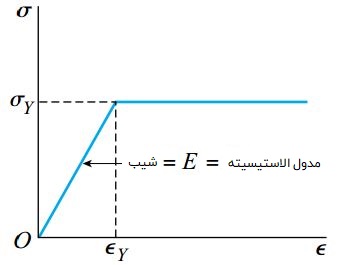
در هنگام اعمال بار کششی بر روی یک میله منشوری از جنس ماده الاستو پلاستیک، شکل منحنی بار-جابجایی شبیه به منحنی تنش-کرنش میشود (شکل زیر). در ابتدای این منحنی، طول میله به صورت الاستیک خطی و طبق قانون هوک تغییر میکند. از اینرو، تغییرات طول در ناحیه مذکور از طریق رابطه δ=PL/EA به دست میآید. هنگامی که ماده به تنش تسلیم میرسد، طول میله بیشتر میشود؛ بدون اینکه افزایشی در میزان بار رخ دهد.
در این شرایط، تغییر طول میله هیچ مقدار مشخصی ندارد. میزان بار در لحظه شروع تسلیم، «بار تسلیم» (Yield Load) و تغییر طول حاصل از آن، «جابجایی تسلیم» (Yield Displacement) نام دارد. توجه داشته باشید که بار تسلیم (PY) برای یک میله منشوری برابر با σYA و جابجایی تسلیم (δY) برای این میله برابر با σYL/E یا PYL/EA است. این روابط در شرایط بارگذاری فشاری نیز قابل استفاده هستند.
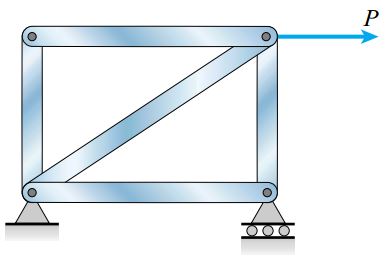
در یک سازه معین استاتیکی که عضوهای آن تحت بارهای محوری قرار دارند، رفتار کلی سازه از الگویی مشابه با منحنی بالا تبعیت میکند. رفتار این نوع سازه تا پیش از رخ دادن تسلیم در یکی از عضوها، به صورت الاستیک خطی است. با رخ دادن تسلیم در یک عضو، طول آن بدون تغییر در میزان بار محوری افزایش مییابد. به این ترتیب، کل سازه در معرض تسلیم قرار میگیرد و شکل منحنی بار-جابجایی آن شبیه به منحنی یک میله میشود.
سازههای نامعین استاتیکی
در یک سازه نامعین استاتیکی که از مواد الاستو پلاستیک ساخته شده است، تحلیل رفتار سازه پیچیدهتر میشود. هنگام رخ دادن تسلیم در یکی از عضوهای این نوع سازه، عضوهای دیگر در برابر هرگونه افزایش بار مقاومت میکنند. با ادامه افزایش میزان بار و تسلیم عضوهای بیشتر، کل سازه در معرض تسلیم قرار میگیرد.
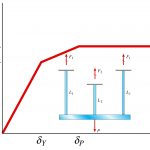
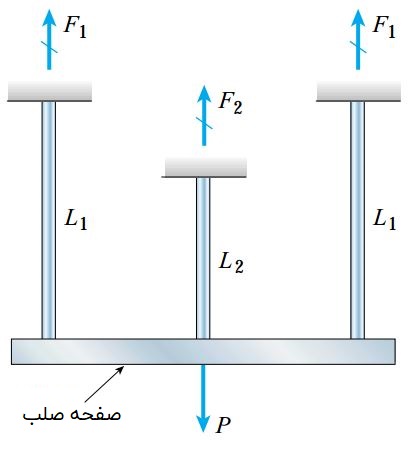
برای آشنایی با رفتار یک سازه نامعین استاتیکی، تصویر زیر را در نظر بگیرید. این سازه از سه میله فولادی متصل به یک صفحه صلب تشکیل شده است. بار P به صفحه صلب اعمال میشود. طول دو میله کناری L1 و طول میله میانی L2 است. هر سه میله دارای سطح مقطع یکسان هستند.
شکل زیر، منحنی تنش-کرنش ایدهآل برای فولاد تشکیلدهنده میلههای سازه بالا را نمایش میدهد. مدول الاستیسیته در ناحیه الاستیک خطی برابر با E=σY/εY است.

تحلیل سازههای نامعین استاتیکی، با تعیین معادلات تعادل و سازگاری شروع میشود. با توجه به تعادل صفحه صلب در راستای عمودی داریم:

F1: نیروی محوری در میلههای کناری؛ F2: نیروی محوری در میله میانی
با شروع بارگذاری، صفحه صلب به سمت پایین حرکت میکند. به این ترتیب، معادله سازگاری به صورت زیر خواهد بود:

δ1: تغییر طول میلههای کناری؛ δ2: تغییر طول میله میانی
روابط بالا تنها به تعادل و هندسه سازه بستگی دارند. به همین دلیل، این روابط برای تمامی مقادیر P معتبر هستند و به قرارگیری کرنش در ناحیه الاستیک خطی یا ناحیه پلاستیک وابسته نیستند. در صورت کوچک بودن بار P، میزان تنشهای موجود در میلهها کمتر از تنش تسلیم σY خواهد بود و ماده در محدوده الاستیک خطی قرار خواهد گرفت. بنابراین، رابطه نیرو-جابجایی (رابطه بین نیروها و تغییر شکلهای به وجود آمده) به صورت زیر بیان میشود:

با جایگذاری روابط بالا در معادلات سازگاری، داریم:

با حل همزمان روابط بالا و معادلات تعادل، به روابط زیر میرسیم:

به این ترتیب، نیروهای درون میلهها در محدوده الاستیک خطی تعیین میشوند. مقادیر تنشهای حاصل از این نیروها نیز با استفاده از روابط زیر به دست میآیند:

معادلات به دست آمده برای نیروها و تنشها در صورتی قابل استفاده هستند که تنشهای درون هر سه میله زیر حد تسلیم قرار داشته باشند. با افزایش تدریجی بار P تا لحظه رخ دادن تسلیم در یکی از میلهها (میلههای کناری یا میله داخلی)، تنشهای درون میلهها افزایش مییابند.
فرض کنید که مطابق شکل زیر میلههای کناری از میله میانی بلندتر باشند. در این وضعیت، تنشهای ایجاد شده در میله میانی نسبت به میلههای کناری بیشتر است. به این ترتیب، میله میانی زودتر از دو میله دیگر به تنش تسلیم میرسد. با رسیدن به نقطه تسلیم، نیروی درون میله میانی F2=σYA خواهد بود. مقدار بار P در هنگام رسیدن هر یک از میلهها به تنش تسلیم با عنوان بار تسلیم (PY) شناخته میشود.


با قرار دادن σYA در روابط مربوط به محاسبه نیروها، مقدار PY از طریق رابطه زیر تعیین میشود:
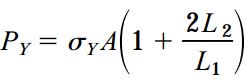
تا زمانی که بار P کمتر از PY باشد، سازه به صورت الاستیک خطی رفتار میکند و روابط ارائه شده برای محاسبه نیروها قابل استفاده هستند. جابجایی رو به پایین میله در بار تسلیم با عنوان جابجایی تسلیم (δY) شناخته میشود. این جابجایی با تغییر طول میله میانی در هنگام رسیدن به تنش تسلیم برابر است:

شکل زیر، رابطه بین بار اعمال شده P و جابجایی δ در منحنی بار-جابجایی سازه بالا را نمایش میدهد. خط OA، بیانگر رفتار سازه تا لحظه رسیدن به تنش تسلیم PY است. با افزایش بار پس از نقطه A، نیروهای F1 در میلههای کناری افزایش مییابند اما نیروی F2 در میله میانی در مقدار σYA ثابت باقی میماند؛ چراکه این میله اکنون به صورت پلاستیک کامل رفتار میکند.

هنگامی که نیروهای F1 به مقدار σYA میرسند، میلههای کناری نیز تسلیم میشوند و در نتیجه، مقاومت سازه در برابر تحمل بارهای اضافی از بین میرود. در این بارگذاری ثابت، طول هر سه میله به صورت پلاستیک تغییر میکند. به میزان بار در این حالت، «بار پلاستیک» (Plastic Load) گفته میشود.
در منحنی بار-جابجایی بالا، مختصات بار پلاستیک (PP) توسط نقطه B نمایش داده شده است. خط افقی BC نیز ناحیه تغییر شکل پلاستیک پیوسته در شرایط بارگذاری ثابت را نشان میدهد. بار پلاستیک PP را میتوان با استفاده از معادلات تعادل استاتیکی محاسبه کرد. برای این منظور در ابتدا معادلات زیر را در نظر میگیریم:

بر اساس معادلات تعادل داریم:

در نتیجه:

جابجایی پلاستیک δP در لحظه رسیدن به بار پلاستیک PP، با تغییر طول میلههای کناری در لحظه رسیدن به تنش تسلیم برابر است. در نتیجه:

با مقایسه δP و δY مشاهده میشود که در این مثال، نسبت جابجایی پلاستیک به جابجایی تسلیم به صورت زیر است:

به علاوه، نسبت بار پلاستیک به بار تسلیم نیز به صورت زیر است:

به طور کلی، نسبت جابجاییها همیشه بزرگتر از نسبت بارهای به وجود آورنده آنها و شیب خط AB در ناحیه نیمه پلاستیک منحنی بار-جابجایی همیشه کوچکتر از شیب خط OA است. علاوه بر این، کوچکترین شیب منحنی نیز به بخش BC در ناحیه پلاستیک کامل تعلق دارد (شیب صفر).

نکات تکمیلی راجع به تحلیل الاستو پلاستیک
برای درک دلایل خطی بودن منحنی بار-جابجایی در ناحیه نیمه پلاستیک (خط AB) و کمتر بودن شیب آن نسبت به ناحیه الاستیک، توضیحات مختلفی وجود دارد. در ناحیه نیمه پلاستیک، میلههای کناری به صورت الاستیک خطی رفتار میکنند. از اینرو، میزان تغییر طول، یک تابع خطی از تغییرات بار است.
به دلیل یکسان بودن جابجایی رو به پایین در صفحه صلب و میلهها، جابجایی صفحه صلب نیز باید یک تابع خطی از تغییرات بار باشد. با توجه به این نکات، بین نقاط A و B یک خط راست ایجاد میشود. اگرچه، شیب منحنی بار-جابجایی در این محدوده کمتر از شیب محدوده اولیه منحنی است. در این محدوده، میله میانی با تسلیم پلاستیک مواجه میشود و تنها میلههای کناری در برابر افزایش بار مقاومت میکنند. در واقع، رفتار سازه در این محدوده به دلیل کاهش سختی آن است.
در مبحث تعیین بار پلاستیک PP مشاهده کردیم که برای محاسبه این پارامتر تنها به استفاده از قواعد استاتیک نیاز خواهیم داشت؛ چراکه در محدوده پلاستیک، تمام عضوها با تسلیم مواجه خواهند شد و نیروهای محوری هر یک از آنها نیز مقادیر مشخصی خواهند داشت. بر خلاف فرآیند تعیین بار پلاستیک PP، محاسبه بار تسلیم PY نیازمند اجرای یک تحلیل نامعین استاتیکی و استفاده از معادلات تعادل، سازگاری و نیرو-جابجایی است.
پس از رسیدن به بار پلاستیک PP، تغییر شکل سازه مطابق خط BC بر روی منحنی بار-جابجایی ادامه پیدا میکند. سپس، پدیده سختشوندگی کرنش در آن رخ میدهد. در این محدوده، قابلیت تحمل بارهای اضافی در سازه افزایش مییابد. با این وجود در اکثر مواقع، تشکیل جابجاییهای بزرگ به معنای از بین رفتن کاربری سازه است. به همین دلیل در تحلیل و طراحی سازهها، بار پلاستیک PP معمولاً به عنوان بار شکست در نظر گرفته میشود.
در مطالب ارائه شده، رفتار یک سازه در هنگام بارگذاری اولیه را مورد بررسی قرار دادیم. در صورت اجرای باربرداری پیش از رسیدن به حد تسلیم، رفتار سازه به صورت الاستیک خطی خواهد بود. در این حالت، سازه به وضعیت اولیه خود بازمیگردد. اگرچه، در صورت اجرای باربرداری پس از حد تسلیم، مقداری تغییر شکل دائمی در برخی از عضوهای سازه باقی میماند و یک وضعیت پیشتنیده در سازه ایجاد میشود. در این حالت، به دلیل وجود تنشهای پسماند، رفتار سازه پس از بارگذاری مجدد تغییر میکند.
مثال
سازه نمایش داده شده در شکل زیر را در نظر بگیرید. این سازه از یک تیر افقی صلب (AB) و دو میله عمودی از جنس ماده الاستوپلاستیک تشکیل شده است. با توجه به اطلاعات نمایش داده شده در این شکل، موارد الف تا ج را تعیین کنید.
- الف) بار تسلیم PY و جابجایی تسلیم δY در نقطه B
- ب) بار پلاستیک PP و جابجایی پلاستیک δP در نقطه B
- ج) منحنی بار-جابجایی (جابجایی δB در نقطه B نسبت به تغییرات بارِ P)

معادلات تعادل
سازه نمایش داده شده در شکل بالا از نظر استاتیکی نامعین است. از اینرو، باید حل مسئله را با نوشتن معادلات تعادل و سازگاری شروع کنیم. با در نظر گرفتن تعادل در تیر AB، گشتاورهای حول نقطه A به صورت زیر خواهد بود:

F1: نیروی محوری در میله 1؛ F2: نیروی محوری در میله 2
رابطه بالا را به صورت زیر ساده میکنیم:

معادلات سازگاری
معادله سازگاری بر اساس هندسه سازه نوشته میشود. با اعمال بارِ P، تیر حول نقطه A دوران میکند. به علاوه، جابجایی رو به پایین در تمام نقاط تیر نسبت به فاصلهشان تا نقطه A متناسب است. به این ترتیب، معادله سازگاری به صورت زیر خواهد بود:

δ1: تغییر طول در میله 1؛ δ2: تغییر طول در میله 2
الف) محاسبه بار و جابجایی تسلیم
در هنگام کوچک بودن بارِ P و قرار داشتن ماده در محدوده الاستیک خطی، رابطه بین نیرو و جابجایی در دو میله به صورت زیر است:

با ترکیب این روابط با معادلات سازگاری داریم:

اکنون روابط بالا را در معادلات تعادل جایگذاری میکنیم:

با توجه به روابط بالا، به دلیل بزرگتر بودن نیروی درون میله دوم (F2)، این میله قبل از میله اول به تنش تسلیم میرسد. در لحظه رخ دادن تسلیم، نیروی درون میله دوم برابر با F=σYA خواهد بود. با جایگذاری این مقدار در روابط بالا، بار تسلیم به صورت زیر تعیین خواهد شد:

تغییر طول حاصل از اعمال بار تسلیم در میله دوم برابر با δ2=σYL/E است. به این ترتیب، جابجایی تسلیم در نقطه B از رابطه زیر به دست خواهد آمد:

ب) محاسبه بار و جابجایی پلاستیک
با رسیدن به بار پلاستیک PP، هر دو میله به تنش تسلیم میرسند. در این وضعیت، مقدار F1 و F2 با σYA برابر است. با توجه معادلات تعادل، بار پلاستیک به صورت زیر تعیین میشود:

در لحظه رسیدن به بار پلاستیک، میله اول به تنش تسلیم میرسد. به این ترتیب، تغییر طول آن با δ1=σYL/E برابر خواهد بود. جابجایی پلاستیک در نقطه B نیز از رابطه زیر محاسبه خواهد شد:

در این مثال، نسبت بار پلاستیک به بار تسلیم، 1.2 و نسبت جابجایی پلاستیک به جابجایی تسلیم 2 است.
ج) رسم منحنی بار-جابجایی
با توجه به مقادیر به دست آمده در بخشهای الف و ب مسئله، منحنی بار-جابجایی به صورت زیر رسم میشود. رفتار سازه از نقطه O تا A به صورت الاستیک خطی، از A تا B به صورت نیمه پلاستیک و از B تا C به صورت کاملاً پلاستیک است.

^^












