روش المان مجزا (Discrete Element Method) – آشنایی با ویژگی های DEM

«روش المان مجزا» (Discrete Element Method) یا اصطلاحاً «DEM»، یکی از روش‌های عددی برای محاسبه فعل و انفعالات تعداد زیادی از ذرات کوچک است. با وجود رابطه بسیار نزدیک DEM با روش شبیه‌سازی «دینامیک مولکولی» (Molecular Dynamics)، ویژگی‌هایی نظیر در نظر گرفتن درجه آزادی دورانی (چرخشی)، وضعیت تماس بین ذرات و هندسه پیچیده، این رویکرد را به طور کلی با گزینه‌های دیگر متمایز می‌کنند.

با پیشرفت قدرت محاسباتی کامپیوترها و توسعه الگوریتم‌های عددی برای مرتب‌سازی به روش نزدیک‌ترین همسایگی، امکان شبیه‌سازی میلیون‌ها ذره با به کارگیری تنها یک پردازنده فراهم شد. امروزه، مقبولیت روش المان مجزا به عنوان یک رویکرد کارآمد برای حل مسائل مهندسی در محیط‌های ناپیوسته و مواد دانه‌ای (مانند مکانیک سنگ، مکانیک مواد پودری، جریان مواد دانه‌ای و غیره) در حال افزایش است. با در نظر گرفتن اصول ترمودینامیکی در DEM و ترکیب آن با دینامیک سیالات محاسباتی (CFD) و روش المان محدود (FEM)، «روش المان مجزای تعمیم یافته» (Extended Discrete Element Method) یا اصطلاحاً «XDEM» در سال‌های اخیر توسعه یافت.

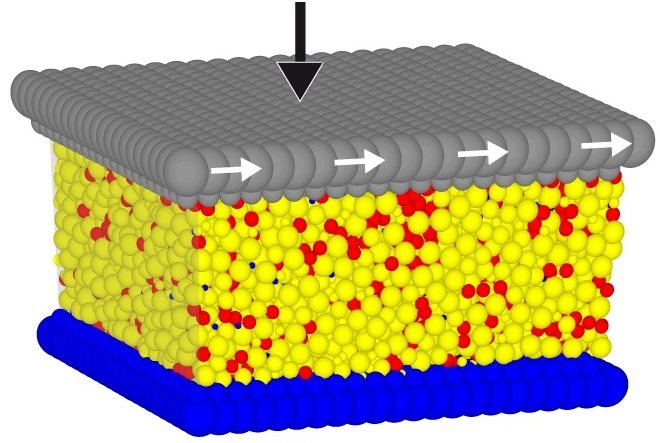
روش‌های المان مجزا از نظر محاسباتی بسیار زمان‌بر هستند. این مسئله، مدت زمان شبیه‌سازی و یا تعداد ذرات مدل را با محدودیت مواجه می‌کند. برخی از کدهای DEM همانند کدهای دینامیک مولکولی از قابلیت پردازش موازی بهره می‌برند. این ویژگی، مدت زمان شبیه‌سازی و تعداد ذرات مدل را بهبود می‌بخشد. در روش‌های دیگر، به جای بررسی رفتار هر ذره، میانگین رفتار فیزیکی تعداد زیادی از ذرات به صورت یک محیط پیوسته ارزیابی می‌شود.

در رویکرد پیوسته برای مواد دانه‌ای با رفتاری مشابه مواد جامد (مکانیک جامدات)، معمولاً ماده به صورت الاستیک یا الاستو پلاستیک در نظر گرفته می‌شود. مدل‌سازی در این حالت با استفاده از یک روش المان محدود یا «روش بدون مش» (Mesh Free Method) صورت می‌گیرد. در رویکرد پیوسته برای جریان‌های دانه‌ای مایع یا گازی شکل، ماده به عنوان یک سیال در نظر گرفته شده و از CFD برای تحلیل رفتار آن استفاده می‌شود. اگرچه، اشکالات مختلفی برای همگن‌سازی مواد در مقیاس دانه‌ای وجود دارد که باید پیش از استفاده از رویکردهای پیوسته مورد بررسی قرار گیرند.

تاریخچه انواع روش‌های المان مجزا

روش المان مجزا، روش المان مجزای تعمیم یافته، «تحلیل تغییر شکل ناپیوسته» (Discontinuous Deformation Analysis) و «روش المان محدود-مجزا» (Finite-Discrete Element Method)، اعضای خانواده DEM را تشکیل می‌دهند. روش عمومی المان مجزا در سال 1971 توسط «کاندال» (Cundall) و برای حل مسائل مکانیک سنگ توسعه یافت. مبنای تئوری این روش در سال 1697 توسط نیوتن پایه ریزی شده بود. در سال 1985، «ویلیامز» (Williams)، «هاکینگ» (Hocking) و «ماستو» (Mustoe) نشان دادند که می‌توان DEM را به عنوان یک روش المان محدود تعمیم یافته در نظر گرفت.

کاربردهای این رویکرد برای مسائل ژئومکانیکی در کتاب «Numerical Methods in Rock Mechanics» تشریح شده است. به علاوه، کتاب «The Combined Finite-Discrete Element Method» نیز اطلاعات جامعی را در مورد روش المان محدود-مجزای ترکیبی ارائه می‌کند.

کاربردهای روش المان مجزا

یکی از فرضیات اصلی روش المان مجزا، وجود ذرات مجزا درون ماده مورد بررسی است. این ذرات می‌توانند شکل و خواص متفاوتی داشته باشند؛ به عنوان مثال:

• مایعات و محلول‌ها مانند شکر یا پروتئین‌ها
• مواد فله‌ای در مخازن ذخیره‌سازی مانند غلات
• مواد دانه‌ای مانند شن
• پودرها مانند تونر
• توده سنگ‌های بلوکی یا درزه‌دار

صنایع مختلفی از روش المان مجزا برای حل مسائل پیش روی خود استفاده می‌کنند. برخی از این صنایع عبارت‌اند از:

• کشاورزی و حمل مواد غذایی
• صنایع شیمیایی
• مهندسی عمران
• صنایع نفتی و گازی
• معدنکاری
• فرآوری مواد معدنی
• داروسازی
• متالورژی پودر

فرآیند کلی روش المان مجزا

شبیه‌سازی DEM با ایجاد یک مدل، تعیین موقعیت مکانی تمام ذرات و اختصاص سرعت اولیه به هر یک از آن‌ها شروع می‌شود. محاسبه نیروهای اعمال شده به هر یک از ذرات با کمک داده‌های اولیه، قوانین فیزیک و مدل‌های مرتبط با سطح تماس صورت می‌گیرد. به طور کلی، یک شبیه‌سازی DEM دارای سه مرحله زیر است:

فیلم آموزش مقدماتی نرم افزار FLAC2D و برنامه نویسی FISH برای تحلیل های عددی در فرادرس

کلیک کنید

1. «مقداردهی اولیه» (Initialization)
2. «تعیین گام زمانی» (Explicit Time-Stepping)
3. «پس پردازش» (Post Processing)

معمولاً به منظور کاهش تعداد سطوح تماس مشترک و توان محاسباتی مورد نیاز، از یک فرآیند مرتب‌سازی به روش نزدیک‌ترین همسایگی در مرحله تعیین گام زمانی استفاده می‌شود. این فرآیند اغلب در بازه‌های زمانی مشخص صورت می‌گیرد. امکان در نظر گرفتن نیروهای زیر در شبیه‌سازی‌های ماکروسکوپی وجود دارد:

• اصطکاک: هنگامی که دو ذره با هم تماس پیدا می‌کنند.
• پلاستیسیته سطح تماس یا «پس‌زنی» (Recoil): هنگامی که دو ذره با هم برخورد می‌کنند.
• جاذبه: نیروی جاذبه بین دو ذره با توجه به جرم آن‌ها در نظر گرفته می‌شود. این نیرو تنها برای شبیه‌سازی در مقیاس‌های بزرگ (مقیاس سیارات) به کار می‌رود.
• پتانسیل کششی: چسبندگی داخلی، اتصال ذرات مایع، جاذبه الکترواستاتیکی و غیره، نمونه‌هایی از نیروی پتانسیل محسوب می‌شوند. توجه داشته باشید که به دلیل سربار محاسباتی ناشی از تعیین نزدیک‌ترین همسایگی جفت ذرات، به دست آوردن نتایج دقیق نیروهای بلند برد (در مقایسه با اندازه ذرات) امکان افزایش زمان محاسبات و الگوریتم‌های مورد نیاز برای حل مسئله وجود دارد.

نیروهای زیر نیز معمولاً که در مقیاس مولکولی در نظر گرفته می‌شوند:

• «نیروی کولن» (Coulomb Force): جاذبه الکترواستاتیکی یا دافعه ذرات حامل بار الکتریکی را نشان می‌دهد.
• «دافعه پاولی» (Pauli Repulsion): در هنگام نزدیک شدن دواتم به یکدیگر ایجاد می‌شود.
• «نیروی واندروالسی» (Van der Waals Force): اتم‌ها را در مولکول‌ها کنار یکدیگر نگه می‌دارد.

تمام نیروهای بالا برای تعیین نیروی اعمال شده بر هر یک از ذرات با هم جمع می‌شوند. به منظور محاسبه تغییرات مکانی و سرعت هر ذره در طول یک گام زمانی، یک روش انتگرال‌گیری مبتنی بر قوانین حرکتی نیوتن مورد استفاده قرار می‌گیرد. سپس، موقعیت‌های مکانی جدید برای محاسبه نیروهای گام بعدی به کار می‌روند. این فرآیند به صورت یک حلقه ادامه می‌یابد تا نتیجه نهایی شبیه‌سازی به دست آید.

برخی از روش‌های انتگرالی مورد استفاده در روش المان مجزا عبارت‌اند از:

• «الگوریتم ورلت» (Verlet Algorithm)
• «الگوریتم سرعت ورلت» (Verlet Velocity Algorithm)
• «انتگرال‌گیری سیمپلکتیک» (Symplectic Integration)
• «انتگرال‌گیری لیپفراگ» (Leapfrog Integration)

نیروهای بلند برد

هنگامی که نیروهای بلند برد (عموماً نیروی جاذبه یا نیروی کولن) در نظر گرفته شوند، فعل و انفعالات بین هر جفت ذره باید مورد محاسبه قرار گیرد. در این حالت، تعداد فعل و انفعالات و هزینه محاسبه نسبت به تعداد ذرات موجود در مدل با مرتبه دو افزایش می‌یابد. این شرایط برای شبیه‌سازی مدل‌هایی با ذرات زیاد مناسب نیست. یکی از روش‌های موجود برای اجتناب از این مشکل، ادغام برخی از ذرات (ذراتی با فاصله زیاد از ذره مورد نظر) به درون یک شبه ذره است. به عنوان مثال واکنش بین یک ستاره و یک کهکشان دور را در نظر بگیرید.

فیلم مجموعه آموزش مهندسی معدن و ژئوتکنیک – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

در این وضعیت، خطای ناشی از ترکیب تمام ستاره‌های موجود در کهکشان دور به درون یک جرم نقطه‌ای بسیار ناچیز خواهد بود. به منظور انتخاب ذرات مستعد برای ادغام درون یک شبه ذره از الگوریتم‌هایی موسوم به الگوریتم‌های درختی استفاده قرار می‌شود. این الگوریتم‌ها تمام ذرات را در یک ساختار درختی قرار می‌دهند. «چاردرخت» (Quadtree) مسائل دوبعدی و «درخت هشت‌تایی» (Octree) در مسائل سه‌بعدی مورد استفاده قرار می‌گیرند.

در شبیه‌سازی به روش دینامیک مولکولی، فضای شبیه‌سازی به سلول‌های کوچک تقسیم‌بندی می‌شود. ذراتی که خارج از محدوده یک طرف قرار داشته باشند، به طرف دیگر منتقل خواهند شد (شرایط مرزی تناوبی). این مسئله برای نیروها نیز صادق است. اگر نیرو در فاصله‌ای دورتر از فاصله حدی (نصف طول یک سلول) قرار گیرد، اثر آن در محاسبات در نظر گرفته نخواهد شد. بنابراین، ذرات تحت تأثیر انعکاس خود در طرف دیگر سلول قرار نمی‌گیرد. به این ترتیب می‌توان تنها با کپی کردن سلول‌ها تعداد ذرات را افزایش داد. الگوریتم‌هایی زیر در نیروی بلند مورد استفاده قرار می‌گیرند:

• «شبیه‌سازی بارنز-هات» (Barnes–Hut Simulation)
• «روش چندقطبی سریع» (Fast Multipole Method)

مزایا و معایب روش المان مجزا

در این بخش، برخی مزایا و محدودیت‌های روش المان مجزا می‌پردازیم. مزایای DEM عبارت هستند از:

• DEM برای شبیه‌سازی طیف گسترده‌ای از جریان‌های دانه‌ای و مسائل مکانیک سنگ قابل استفاده است. گروه‌های تحقیقاتی مختلفی به طور مستقل نرم‌افزارهای شبیه‌سازی متنوعی را توسعه داده‌اند. این نرم‌افزارها با یافته‌های آزمایشگاهی موجود در تعداد زیادی از مسائل مهندسی نظیر پودرهای چسبنده، جریان دانه‌ای و توده سنگ‌های درزه‌دار مطابقت دارند.
• DEM امکان مطالعات جزئی بیشتری بر روی میکرو دینامیک جریان‌های پودری فراهم می‌کند؛ در صورتی که این مطالعات معمولاً با آزمایش‌های فیزیکی صورت می‌گیرد. برای مثال شبکه‌های نیروی شکل گرفته در یک محیط دانه‌ای را می‌توان به وسیله DEM نمایش داد. باید توجه داشت که این‌گونه اندازه‌گیری‌ها در آزمایش‌هایی با ذرات کوچک و زیاد، تقریباً غیرممکن است.

از محدودیت‌های DEM نیز می‌توان به موارد زیر اشاره کرد:

• حداکثر تعداد ذرات و مدت زمان شبیه‌سازی به توان محاسباتی تجهیزات موجود بستگی دارد. جریان‌های معمولی شامل میلیاردها ذره هستند. با این وجود، حل مسائلی با این مقیاس بزرگ با استفاده از شبیه‌سازهای DEM بر روی تجهیزات بزرگ رایانش خوشه‌ای در سال‌های اخیر و با صرف مدت زمان مناسب (زمان شبیه‌سازی نه زمان واقعی اجرای برنامه) امکان‌پذیر شده است.
• روش المان مجزا از نظر محاسباتی وقت‌گیر است. به همین دلیل، این رویکرد در مسائل مهندسی و صنعتی مرتبط با محیط‌های پیوسته به طور گسترده مورد استفاده قرار نمی‌گیرد. با این وجود، در صورت استفاده از واحدهای پردازش گرافیکی (GPU) برای اجرای شبیه‌سازی‌های DEM، به دلیل وجود هسته‌های محاسباتی متعدد بر روی این واحدها، امکان کاهش زمان واقعی اجرای برنامه وجود خواهد داشت. علاوه بر این، در هنگام اجرای روش المان مجزا، کارایی و بهره‌وری واحدهای پردازش گرافیکی از نظر صرف انرژی نسبت به خوشه‌های محاسباتی بیشتر است (انرژی کمتری مصرف می‌شود).

نرم‌افزارهای مبتنی بر DEM

در این بخش فهرستی از نرم‌افزارهای متن‌باز و تجاری مبتنی بر روش المان مجزا را برای شما ارائه می‌کنیم.

نرم‌افزارهای متن‌باز DEM

• BALL & TRUBAL
• Mercury-DPM
• YADE
• LIGGGHTS
• MFIX-DEM
• MechSys

نرم‌افزارهای تجاری DEM

• UDEC & 3DEC
• Chute Maven
• PFC2D & PFC3D
• EDEM
• GROMOS 96
• ELFEN
• PASSAGE
• Bulk Flow Analyst
• Rocky DEM

^^