استوانه و مفاهیم آن در هندسه — به زبان ساده

استوانه یک شیء است که در هندسه کاربردهای بسیاری دارد. در این مقاله با ویژگی‌های این شیء بیشتر آشنا می‌شویم.

هر استوانه دارای خصوصیات زیر است:

• هر دو سر آن صاف هستند.
• هر دو سر آن دقیقا یک شکل هستند.
• از پایین تا بالا، کاملا دارای یک شکل ثابت است.
• یکی از وجه‌های آن منحنی است.
• از آنجایی که یک وجه آن منحنی است، شکل چند وجهی به حساب نمی‌آید.

مساحت استوانه

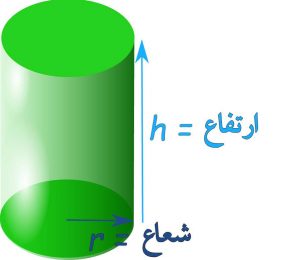
برای به دست آوردن مساحت یک استوانه، به مساحت دو سر، و مساحت بخش میانه نیاز داریم.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

برای به دست آوردن محیط، از فرمول زیر استفاده می‌کنیم:

مساحت دو سر = 2 × π × r²

مساحت بخش میانه = 2 × π × r × h

که مجموع دو فرمول بالا، فرمول زیر را تشکیل می‌دهد:

مساحت استوانه = 2 × (π × r × (r+h

فرض کنید استوانه‌ای داریم که شعاع آن برابر 2 و ارتفاع آن برابر 7 باشد. در این حالت محاسبه‌ی مساحت استوانه به صورت زیر انجام می‌شود:

2 × (π × r × (r+h = مساحت استوانه

2 × (π × 2 × (2+7 =

2 × π × 2 × 9 =

36 π =

113.097 ≈

حجم استوانه

برای محاسبه‌ی حجم استوانه، مساحت یک سر آن را به دست آورده، و در ارتفاع استوانه ضرب می‌کنیم.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

مساحت یک سر = π × r²

ارتفاع = h

که با ضرب این دو داریم:

حجم استوانه = π × r² × h

مثال قبل را در نظر بگیرید. یک استوانه که شعاع آن 2، و ارتفاع آن برابر 7 است. در این حالت محاسبه‌ی حجم استوانه به صورت زیر انجام می‌شود:

π × r² × h = حجم استوانه

π × 2² × 7 =

28 π =

87.96 ≈

برای اینکه بتوانیم راحت‌تر این فرمول را بخاطر بسپاریم، از یک راه حل ساده استفاده می‌کنیم.

یک پیتزا را فرض کنید (که به انگلیسی pizza نوشته می‌شود). حالا شعاع پیتزا را «z» و ضخامت آن‌ را «a» در نظر بگیرید. پس فرمول حجم به صورت زیر در می‌آید:

pi × z × z × a = حجم

که عدد pi را معمولا با نماد «π»، و z × z را با نماد «z²» نشان می‌دهیم، ولی به طور کلی، این فرمول گویای فرمول اصلی است.

مقایسه حجم مخروط و استوانه

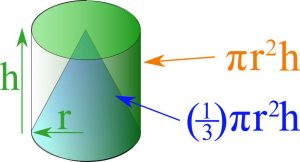
فرمول محاسبه حجم استوانه و مخروط بسیار شبیه‌به‌هم هستند.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

به فرمول‌های زیر توجه کنید:

حجم استوانه = π × r² × h

حجم مخروط = 1/3 × π × r² × h

پس نتیجه می‌گیریم که حجم یک مخروط دقیقا یک سوم (1/3) حجم یک استوانه است.

توجه داشته باشید که یک استوانه حتما قرار نیست دایره‌ای شکل باشد. معمولا وقتی حرف از استوانه می‌زنیم، منظورمان یک استوانه‌ی دایره‌ای شکل است، ولی استوانه‌های بیضی شکل هم داریم.

حتی شکل‌های عجیب‌تری از استوانه‌ها هم وجود دارند. تا زمانی که سطح مقطع شکل ما از یک سر تا سر دیگر یک شکل ثابت باشد، شکل ما یک استوانه است. ولی محاسبات محیط و حجم برای هر شکل متفاوت است. تصاویر زیر، انواع مختلف استوانه را نشان می‌دهند.