گراف قویا همبند و برنامه تشخیص آن – راهنمای کاربردی

در این مطلب، روش نوشتن برنامه‌ای که تشخیص می‌دهد یک گراف قویا همبند است یا خیر، مورد بررسی قرار گرفته است. همچنین، پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C، «جاوا» (Java) و «پایتون» (Python) انجام شده است. فرض می‌شود یک گراف جهت‌دار به عنوان ورودی به برنامه داده شده است. هدف آن است که برنامه بررسی و مشخص کند که آیا گراف قویا هم‌بند است یا خیر. یک گراف جهت‌دار، قویا هم‌بند است اگر مسیری بین هر دو جفت از راس‌های آن وجود داشته باشد. برای مثال، گرافی که در تصویر زیر آمده، قویا هم‌بند محسوب می‌شود.

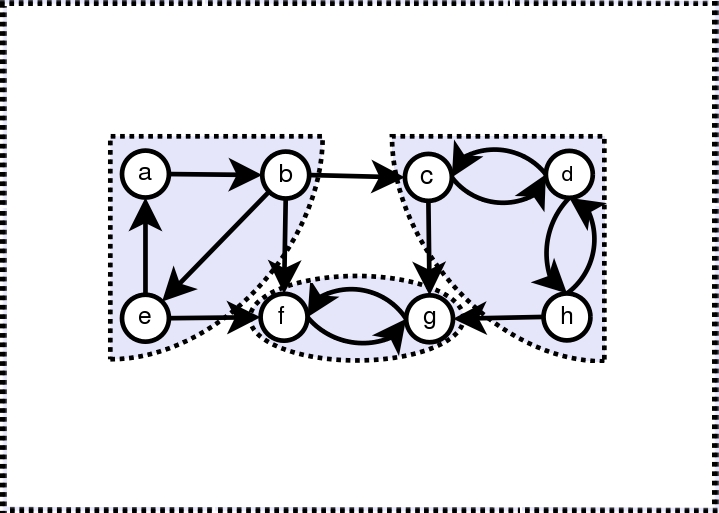
انجام چنین کاری در گراف غیرجهت‌دار آسان است. در این راستا، کافی است که پیمایش «جستجوی اول سطح» (Breadth-First Search | BFS) و «جستجوی اول عمق» (Depth-First Search | DFS) با آغاز از هر راسی انجام شود. اگر در پیمایش BFS یا DFS، همه راس‌ها مشاهده شدند، گراف غیر جهت‌دار همبند است.

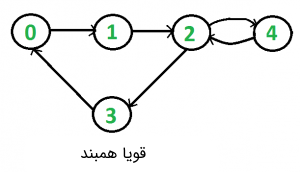
این رویکرد برای گراف‌های جهت‌دار پاسخگو نیست. برای مثال، گراف زیر قویا همبند نیست. اگر پیمایش DFS یا BFS با شروع از راس صفر انجام شود، می‌توان به همه راس‌ها رسید، اما اگر از هر راس دیگری آغاز شود، نمی‌توان به همه راس‌ها رسید.

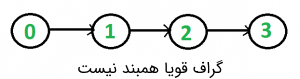
یک ایده ساده آن است که از همه الگوریتم‌های کوتاه‌ترین مسیرها مانند پیدا کردن «بستار تعدی» (Transitive Closure) گراف یا «الگوریتم فلوید-وارشال» (Floyd Warshall) استفاده شود. پیچیدگی زمانی این روش، از درجه (O(v³ است. همچنین، می‌توان DFS را به تعداد V مرتبه با آغاز از هر راسی انجام داد. اگر DFS همه راس‌ها را ملاقات نکرد، گراف قویا همبند نیست. این الگوریتم، ((O(V*(V+E زمان می‌برد که مشابه با بستار تعدی برای گراف چگال است.

یک ایده بهتر، استفاده از الگوریتم «اجزای قویاً هم‌بند» (Strongly Connected Components | SCC) است. می‌توان همه SCC‌ها را در زمان (O(V+E پیدا کرد. اگر تعداد SCC‌ها برابر با یک باشد، گراف قویا هم‌بند است. الگوریتم SCC پس از پیدا کردن همه SCC‌ها، دیگر کاری انجام نمی‌دهد. در ادامه، الگوریتم ساده و مبتنی بر DFS «کساراجو» (Kosaraju) ارائه شده است که دو پیمایش در گراف انجام و تشخیص می‌دهد که گراف قویا همبند است یا خیر. روش کار این الگوریتم، در ادامه بیان شده است.

فیلم آموزش برنامه نویسی C++‎ سی پلاس پلاس + گواهینامه در فرادرس

کلیک کنید

1. همه راس‌ها را با «ملاقات نشده» مقداردهی اولیه کن.
2. پیمایش DFS گراف را با شروع از هر راس دلخواه v آغاز کن. اگر در پیمایش DFS همه راس‌ها ملاقات نشدند، false را بازگردان.
3. همه یال‌ها را معکوس کن (یا ترانهاده یا معکوس گراف را پیدا کن)
4. همه راس‌ها را در گراف معکوس شده با عنوان «ملاقات نشده» علامت‌گذاری کن.
5. پیمایش DFS گراف معکوس را از همان راس v (که در گام ۲ از آن استفاده شد) آغاز کن. اگر پیمایش DFS همه راس‌ها را ملاقات نکرد، مقدار false را بازگردان. در غیر این صورت، مقدار true را بازگردان.

ایده آن است که اگر همه گره‌ها از راس v دسترسی‌پذیر باشند، و هر گره‌ای بتواند به v برسد، گراف قویا هم‌بند است. در گام ۲، بررسی می‌شود که همه راس‌ها از راس v دسترسی‌پذیر هستند. در گام ۴، بررسی می‌شود که آیا می‌توان از همه راس‌ها به راس v رسید (در گراف معکوس، اگر همه راس‌ها از راس v دسترسی‌پذیر باشند، همه راس‌ها می‌توانند در گراف اصلی به راس v برسند). پیاده‌سازی الگوریتم بالا، در ادامه در زبان‌های برنامه‌نویسی گوناگون ارائه شده است.

برنامه تشخیص گراف قویا همبند در ++C

برنامه تشخیص گراف قویا همبند در جاوا

برنامه تشخیص گراف قویا همبند در پایتون

خروجی قطعه کد بالا، به صورت زیر است.

Yes
No

پیچیدگی زمانی روش ارائه شده در بالا، برابر با «جستجوی اول عمق» است و اگر گراف با استفاده از ماتریس مجاورت ارائه شده باشد، از درجه (O(V+E خواهد بود.

این رویکرد نیازمند دو بار پیمایش گراف است. می‌توان با استفاده از «الگوریتم تارژان مؤلفه‌های قویا هم‌بند» (Tarjan's Strongly Connected Components Algorithm)، با یک بار پیمایش گراف این کار را انجام داد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده

^^