الگوریتم بروکا (Boruvka’s Algorithm) – راهنمای کاربردی

در این مطلب، «الگوریتم بروکا» (Boruvka’s Algorithm) مورد بررسی قرار گرفته و پیاده‌سازی آن در زبان‌های برنامه‌نویسی C++/C و پایتون انجام شده است. الگوریتم بروکا نیز مانند «الگوریتم پریم» (Prim's Algorithm) و «الگوریتم کراسکال» (Kruskal Algorithm)، یک «الگوریتم حریصانه» (Greedy Algorithm) است.

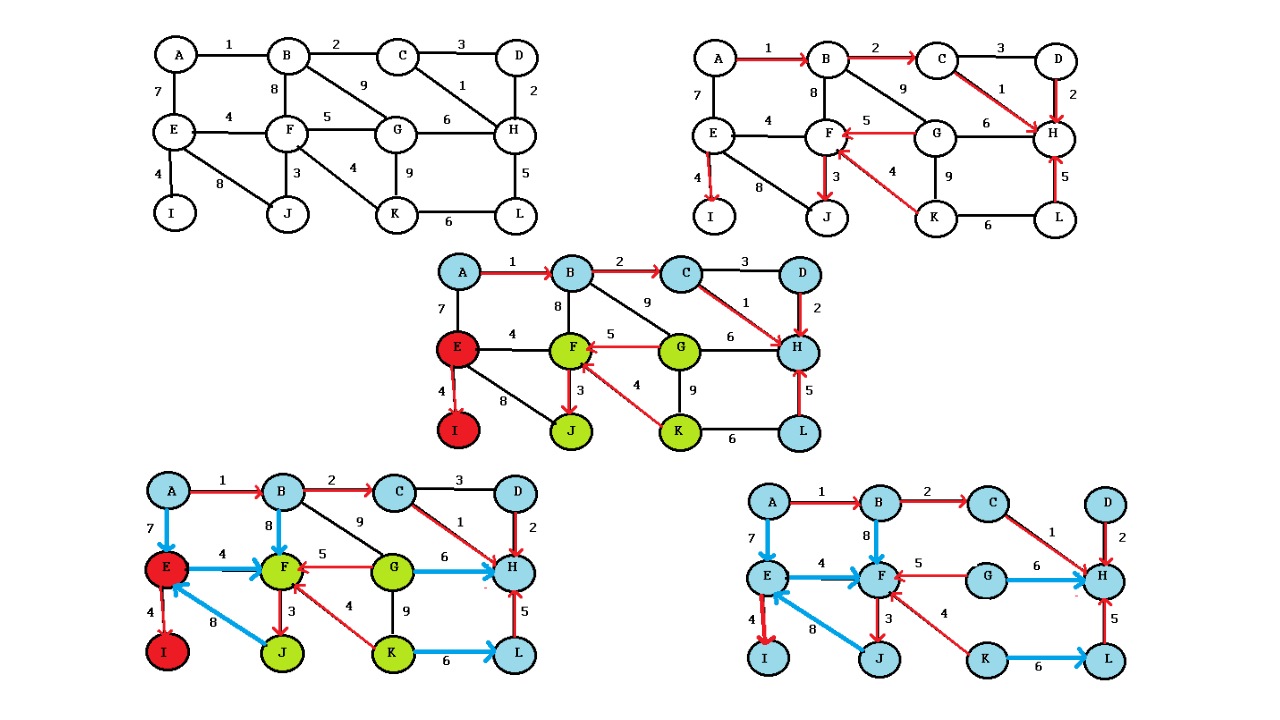
الگوریتم بروکا

در زیر، الگوریتم بروکا به طور کامل ارائه شده است.

1. ورودی، یک گراف متصل، وزن‌دار و غیر جهت‌دار است.
2. همه راس‌ها را به عنوان عنصر‌های مجزا مقداردهی کن.
3. درخت پوشای کمینه را به عنوان empty مقداردهی اولیه کن.
4. در حالیکه بیش از یک عنصر وجود دارد، برای هر عنصر، اقدامات زیر را انجام بده:
   1. یالی با نزدیک‌ترین وزن که این عنصر را به سایر عناصر متصل می‌کند، پیدا کن.
   2. این نزدیک یال را در صورتی که تاکنون به درخت پوشای کمینه اضافه نشده، اضافه کن.
5. درخت پوشای کمینه را بازگردان.

در ادامه، ایده نهفته در پس الگوریتم بروکا، همراه با مثال نمایش داده شده است. شایان ذکر است که ایده این الگوریتم، مانند الگوریتم «درخت پوشای کمینه» (Minimum Spanning Tree) پریم است. منظور از درخت پوشای کمینه آن است که همه راس‌ها متصل باشند. بنابراین، دور زیرمجموعه غیرمتصل (که در بالا تشریح شده است) از راس‌ها باید متصل باشند تا یک درخت پوشا ساخته شود. همچنین، آن‌ها باید با یال دارای حداقل وزن متصل شوند تا از آن یک درخت پوشای کمینه بسازند. در ادامه، مفهوم این الگوریتم با استفاده از مثالی، بیان می‌شود.

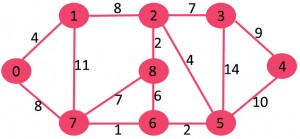
به طور اولیه، MST خالی است. هر راسی یک عنصر مجرد است که با خط آبی در تصویر زیر مشخص شده است.

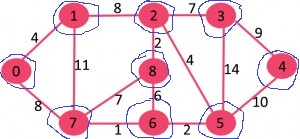
برای هر عنصر، کم‌وزن‌ترین یالی که آن را به دیگر عنصر‌ها متصل می‌کند، یافت می‌شود.

فیلم آموزش روش حریصانه در طراحی الگوریتم (رایگان) در فرادرس

کلیک کنید

Component                Cheapest Edge that connects 
                         it to some other component
  {0}                           0-1
  {1}                           0-1
  {2}                           2-8
  {3}                           2-3
  {4}                           3-4
  {5}                           5-6
  {6}                           6-7
  {7}                           6-7
  {8}                           2-8

سبک‌ترین یال‌ها با رنگ سبز مشخص شده‌اند. اکنون، درخت پوشای کمینه به صورت $${0-1, 2-8, 2-3, 3-4, 5-6, 6-7}$$‎ است.

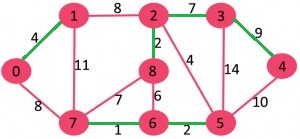
پس از مراحل بالا، عنصر‌ها $${{0,1}, {2,3,4,8}, {5,6,7}}$$ هستند. این عنصر‌ها با دوایر آبی رنگ مشخص شده‌اند.

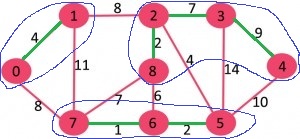
اکنون، مجددا مراحل تکرار می‌شوند. برای هر عنصر، سبک‌ترین یالی که آن را به دیگر عنصر‌ها متصل می‌کند، پیدا می‌شود.

Component                Cheapest Edge that connects 
                         it to some other component
  {0,1}                        1-2 (or 0-7)
  {2,3,4,8}                    2-5
  {5,6,7}                      2-5

سبک‌ترین یال‌ها با رنگ سبز مشخص شده‌اند. اکنون، درخت پوشای کمینه به صورت $${0-1, 2-8, 2-3, 3-4, 5-6, 6-7, 1-2, 2-5}$$‎ است.

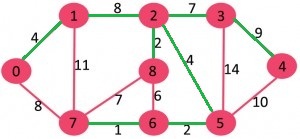
در این گام، تنها یک عنصر {0, 1, 2, 3, 4, 5, 6, 7, 8}‎ وجود دارد که همه یال‌ها را دربر می‌گیرد. با توجه به اینکه تنها یک عنصر باقی مانده است، کار متوقف و درخت پوشای کمینه بازگردانده می‌شود. در ادامه، پیاده‌سازی الگوریتم بروکا در زبان‌های برنامه‌نویسی C++/C و پایتون انجام شده است.

پیاده‌سازی الگوریتم بروکا در C++/C

پیاده‌سازی الگوریتم بروکا در پایتون

فیلم آموزش نکات برنامه نویسی پایتون و حل مسائل الگوریتمی در فرادرس

کلیک کنید

خروجی قطعه کد بالا، به صورت زیر است.

Edge 0-3 included in MST
Edge 0-1 included in MST
Edge 2-3 included in MST
Weight of MST is 19

پیچیدگی زمانی الگوریتم بروکا از درجه O(E log V)‎ و در واقع، مشابه با پیچیدگی الگوریتم کراسکال و پریم است. الگوریتم بروکا یکی از قدیمی‌ترین الگوریتم‌های «درخت پوشای کمینه» (Minimum Spanning Tree) است که در سال ۱۹۲۶ میلادی، مدت‌ها پیش از اینکه کامپیوترها حتی وجود داشته باشند، توسط بورکا کشف شده است. این الگوریتم به عنوان روشی برای ساخت شبکه الکتریسیته موثر، معرفی شده بود.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

^^