پارادوکس چرخ ارسطو – ویدیوی علمی

اگر دو دیسک (چرخ) هم‌‌مرکز متصل به هم که دارای شعاع‌‌های متفاوتی هستند را روی یک سطح صاف بغلتانیم، خواهید دید که هر دوی آن‌‌ها یک چرخش کامل انجام داده و مسافت یکسانی را طی می‌‌کنند. اما اگر دیسک کوچک‌‌تر به تنهایی غلتانده شود، مسافت کوتاه‌‌تری نسبت به حالت قبل طی خواهد کرد. این تناقض که ترکیبی از هندسه و حرکت است، ۲۰۰۰ سال است که ذهن ریاضی‌‌دانان را متوجه خود ساخته است. از آنجایی که محیط دایره از رابطه C=2πr بدست می‌‌آید، واضح است که محیط دیسک بزرگ از محیط دیسک کوچک بزرگ‌‌تر است. پس چگونه ممکن است دیسک کوچک (متصل به دیسک بزرگ)، فقط یک بار بچرخد و مسافتی به اندازه دیسک بزرگ‌‌تر طی کند؟

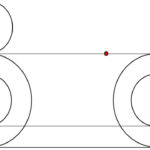
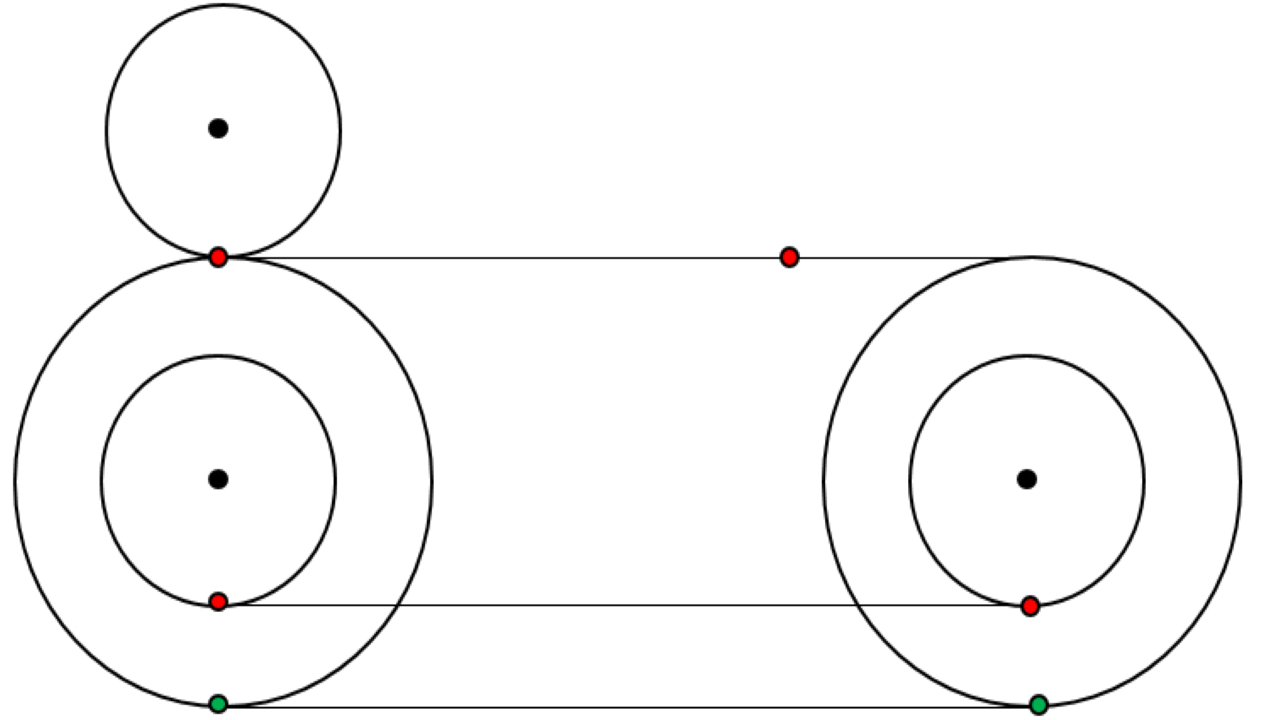
گالیله در کتاب «دو علم جدید» خود راه‌‌حلی برای این مسئله ارائه داد. او این حالت را به صورت شش‌‌ضلعی‌‌های هم‌‌مرکز تقریب زد و حد را برای تعداد اضلاع بیشتر بررسی کرد. برای درک این پارادوکس و یافتن پاسخ آن، شاید بهتر باشد فیزیک غلتش بدون لغزش را نسبت به این حالت که در آن غلتش و لغزش با هم رخ می‌‌دهند، بررسی کنید.