فرادرسنمونه سوال تقسیم چکشی — به زبان ساده با جواب تشریحی
در آموزش‌های قبلی مجله فرادرس، با تقسیم چکشی آشنا شدیم. در این آموزش، ضمن یادآوری روش گام به گام تقسیم چکشی، چند نمونه سوال را از تقسیم چکشی حل می‌کنیم.
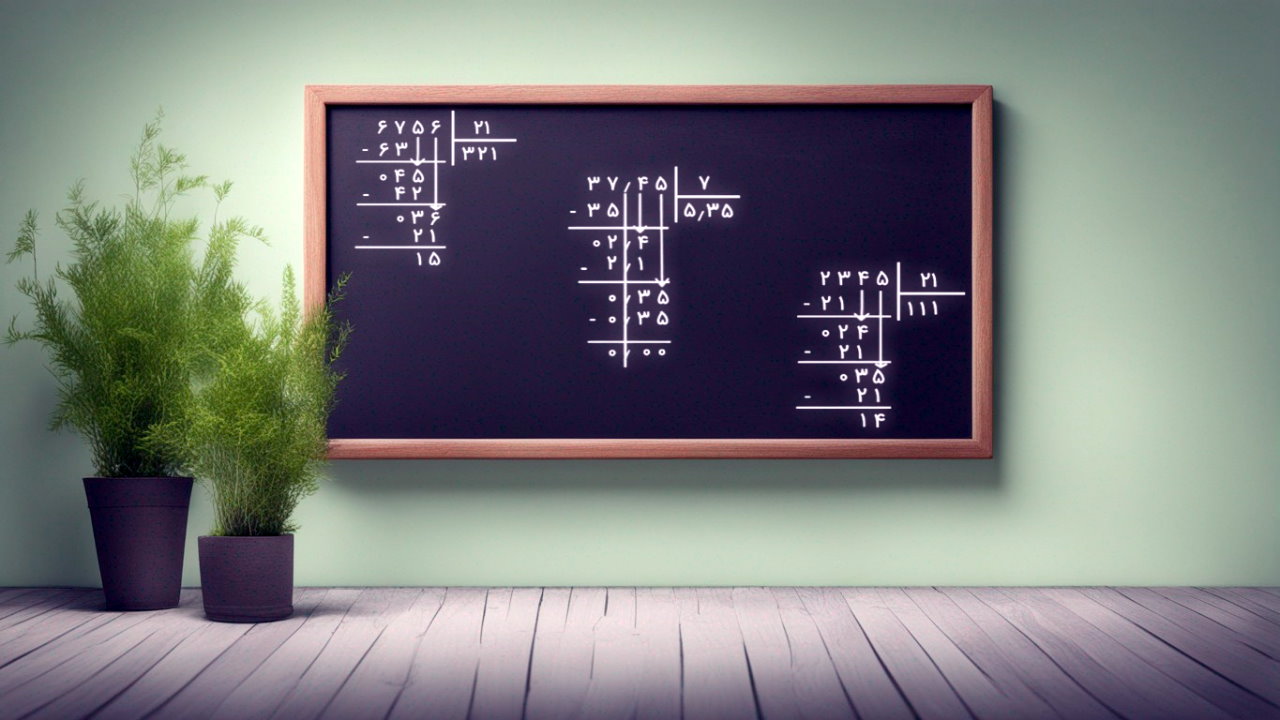
تقسیم چکشی چیست؟
در این بخش، تقسیم چکشی را مرور می‌کنیم. این کار را با یک مثال انجام خواهیم داد. فرض کنید می‌خواهیم عدد ۷۲۰ را بر ۴۰ تقسیم کنیم. ابتدا باید بدانیم که به ۷۲۰ مقسوم می‌گوییم و به ۴۰ مقسوم‌علیه. برای آشنایی بیشتر با این اصطلاحات، به آموزش «مقسوم ، مقسوم علیه و باقیمانده چیست؟ — به زبان ساده» مراجعه کنید. برای اینکه تقسیم را انجام دهیم، ابتدا آن را به‌شکل مناسب می‌نویسیم که تصویر زیر آن را نشان می‌دهد.
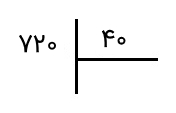
اکنون، گام به گام این تقسیم را حل می‌کنیم. قبل از هر چیزی، تعداد ارقام مقسوم‌علیه را می‌بینیم. در اینجا، عدد ۴۰ دو رقم دارد. پس، به‌اندازه تعداد ارقام آن از سمت چپ از مقسوم جدا می‌کنیم و بررسی می‌کنیم که عددی را که جدا کرده‌ایم، بزرگ‌تر از ۴۰ باشد. در اینجا عدد ۷۲ از ۴۰ بزرگ‌تر است و نیازی نیست رقم بیشتری را جدا کنیم. پس به‌شکل زیر دو رقم جداشده را مشخص می‌کنیم.
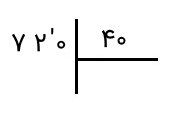
اکنون این پرسش را از خودمان مطرح می‌کنیم که حاصل تقسیم ۷۲ بر ۴۰ چند می‌شود. می‌بینیم که جواب ۱ است، زیرا یک ۴۰ تایی را می‌توانیم از ۷۲ جدا کنیم. اما جواب ۲ نمی‌تواند باشد، چون دو تا ۴۰ تایی ۸۰ می‌شود و بزرگ‌تر از ۷۲ است. اکنون که به رقم ۱ رسیدیم، آن را در خارج قسمت می‌نویسیم.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
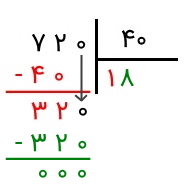
پس از نوشتن رقم مورد نظر در خارج قسمت، آن را در مقسوم‌علیه ضرب می‌کنیم و حاصل را زیر عددی که جدا کرده بودیم، یعنی زیر عدد ۷۲، می‌نویسیم و از آن کم می‌کنیم.
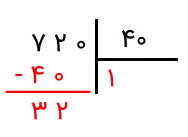
همان‌طور که انتظار داریم، عدد ۳۲ از ۴۰ کوچک‌تر است و نمی‌توان آن را بر ۴۰ تقسیم کرد. پس، یک رقم از مقسوم را که از آن در تقسیم استفاده نکرده بودیم، پایین میآوریم و در کنار ۳۲ قرار می‌دهیم. این یعنی اکنون عدد ۳۲۰ را داریم و باید ۳۲۰ را بر ۴۰ تقسیم کنیم. این پرسش را مطرح می‌کنیم که چند تا ۴۰ تایی در ۳۲۰ قرار دارد. به عدد ۸ می‌رسیم، زیرا ضرب ۴۰ در ۸ برابر با ۳۲۰ می‌شود. بنابراین، رقم ۸ را در کنار رقم ۱ در خارج قسمت می‌نویسیم. پس از نوشتن آن، این رقم را در مقسوم‌علیه ضرب می‌کنیم و حاصل را زیر ۳۲۰ می‌نویسیم و آن را از این عدد کم می‌کنیم. می‌بینیم که حاصل برابر با صفر است. این یعنی اینکه حاصل تقسیم ۷۲۰ بر ۴۰ برابر با ۱۸ بوده و باقیمانده نیز برابر با ۰ است. اینجاست که تقسیم پایان می‌یابد.
نمونه سوال تقسیم چکشی
در این بخش، به نمونه سوال‌های تقسیم چکشی می‌پردازیم.
مثال اول نمونه سوال تقسیم چکشی
حاصل تقسیم ۴۵۲ بر ۷ را محاسبه کنید.
جواب: ابتدا یک رقم از سمت چپ جدا می‌کنیم. می‌بینیم که ۴ از ۷ کوچک‌تر است و به همین دلیل باید یک رقم دیگر را نیز جدا کنیم. بنابراین، رقم ۵ را نیز جدا می‌کنیم. اکنون باید ببینیم چند تا ۷ تایی در ۴۵ وجود دارد. می‌بینیم که پاسخ ۶ است (می‌دانیم که شش هفت تا می‌شود ۴۲ تا). پس عدد ۷ را در خارج‌قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم که حاصلش ۴۲ می‌شود. آن را زیر مقسوم می‌نویسیم و از آن کم می‌کنیم.
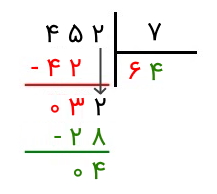
حاصل تفریق ۳ است. با توجه به کوچک‌تر بودن ۳ نسبت به ۷، رقم ۲ را نیز پایین میآوریم و به عدد ۳۲ می‌رسیم. اکنون، حاصل تقسیم ۳۲ بر ۷ برابر با ۴ خواهد بود. ۴ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم. حاصل‌ضرب را که ۲۸ است. عدد ۲۸ را از ۳۲ کم می‌کنیم. جواب ۴ است. چون ۴ از ۷ کوچک‌تر است و رقمی باقی نمانده که پایین بیاوریم، پس تقسیم پایان می‌یابد. در نهایت، خارج قسمت ۶۴ و باقیمانده ۴ است.
مثال دوم نمونه سوال تقسیم چکشی
تقسیم ۳۷٫۴۵ را بر ۷ را انجام دهید.
جواب: بدین منظور، از اعشار یک خط عمودی به پایین رسم می‌کنیم تا مرز اعشار را بشناسیم و تقسیم را به‌درستی انجام دهیم.
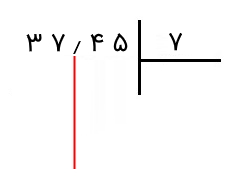
اکنون از سمت چپ شروع می‌کنیم. بخش صحیح عدد را می‌بینیم. مانند دو عدد صحیح، یک رقم از چپ جدا می‌کنیم و می‌بینیم که ۳ کوچک‌تر از ۷ است. پس یک رقم دیگر نیز جدا می‌کنیم. اکنون عدد ۳۷ را داریم.
می‌خواهیم ببینیم چند ۷ در ۳۷ وجود دارد. عدد ۵ جوابی است که به آن می‌رسیم. آن را در خارج قسمت می‌نویسیم. اکنون عدد را در مقسوم‌علیه ضرب می‌کنیم و حاصل آن را زیر بخش صحیح عدد مقسوم‌علیه، یعنی ۳۷، می‌نویسیم. سپس آن را از ۳۷ کم می‌کنیم. حاصل را که ۲ است، زیر آن می‌نویسیم.
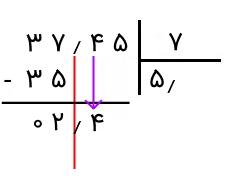
اکنون، مشابه آنچه برای اعداد صحیح انجام می‌دادیم، اعشار و یک رقم از بالا را به پایین میآوریم و کنار رقم ۲ قرار می‌دهیم. همان‌طور که مشخص است، به عدد ۲٫۴ می‌رسیم. نکته‌ای که در اینجا باید به آن دقت کنیم و بسیار مهم است، این است که وقتی اعشار را پایین میآوریم، باید یک اعشار بعد از رقم خارج‌قسمت قرار دهیم.
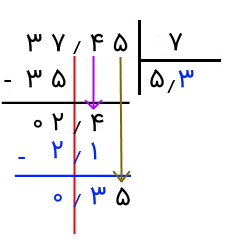
اکنون که بعد از رقم ۵ اعشار گذاشته‌ایم، رقمی که بعد از اعشار قرار گیرد، در واقع ارزش مکانی آن دهم است. در واقع، اکنون ۲٫۴ را بر ۷ تقسیم می‌کنیم و خارج‌قسمت ارزش دهم دارد. برای راحتی می‌توانیم در ذهنمان دو اعشار را به‌طور فرضی حذف کنیم و تقسیم ۲۴ بر ۷ را انجام دهیم و محاسبه نیز درست خواهد بود.
بنابراین، از خودمان می‌پرسیم که چند تا ۷ در ۲۴ قرار دارد و جوابمان رقم ۳ است. دقت کنید که معادل اعشاری این پرسش این‌گونه است: چند تا یک‌دهمِ رقم ۷ در ۲٫۴ قرار دارد که جواب باز هم ۳ است. یک‌دهم ۷ که می‌شود ۰٫۷ و ۳ تا از آن در ۲٫۴ قرار دارد.
پس، ۳ را بعد از اعشار خارج‌قسمت قرار می‌دهیم و آن را در ۷ ضرب می‌کنیم. دقت کنید که داریم ۰٫۳ را در ۷ ضرب می‌کنیم، چون ۳ بعد از اعشار است و ارزش مکانی آن دهم است. در واقع، اکنون باید ۲۷ را بر ۷ تقسیم کنیم. عدد ۳ برای جواب آن مناسب است. بنابراین، گویی همان ۲٫۴ را بر ۷ تقسیم کرده‌ایم و چون اعشار قرار داده‌ایم، عدد خارج قسمت ۰٫۳ است. حال آن ۳ را در ۷ ضرب می‌کنیم که حاصلش می‌شود ۲٫۱. آن را زیر ۲٫۴ می‌نویسیم و از آن کم می‌کنیم.
حاصل برابر با ۰٫۳ خواهد بود. اکنون ۵ را پایین میآوریم و باید ۰٫۳۵ را بر ۷ تقسیم کنیم.
تا حالا خارج قسمت ۵٫۳ است. اکنون، ارزش رقم بعد از ۳ صدم است. یعنی باید از خودمان بپرسیم که چند تا صدم را باید در ۷ ضرب کنیم که حاصلش بشود ۰٫۳۵. جایگاه صدم یعنی دو رقم اعشار و ۰٫۳۵ هم دو رقم اعشار دارد. بنابراین، با توجه به اینکه خارج قسمت در این مرحله دو رقم اعشار دارد و مقسوم جدید، یعنی ۰٫۳۵، نیز دو رقم اعشار دارد، می‌توانیم برای راحتی و به‌دست آوردن رقم خارج قسمت، اعشار را در نظر نگیریم و از خودمان بپرسیم که چند تا ۷ می‌شود ۳۵. جواب ۵ است.
بنابراین، کافی است رقم ۵ را در کنار رقم ۳ در خارج‌قسمت قرار دهیم. در واقع، ۰٫۳۵ را اگر بر ۷ تقسیم کنیم، به عدد ۰٫۰۵ می‌رسیم. به عبارت دیگر، ۰٫۰۵ را اگر در ۷ ضرب کنیم، به عدد ۰٫۳۵ می‌رسیم. با نوشتن این عدد زیر مقسوم جدید، به باقیمانده صفر می‌رسیم.
مثال سوم نمونه سوال تقسیم چکشی
عدد ۱۲٫۷۵ را بر ۰٫۱۱ تقسیم کنید.
جواب: می‌بینیم که دو عدد اعشاری هستند. ساده‌ترین کار این است که این دو عدد را به اعدادی صحیح تبدیل کنیم، سپس تقسیم چکشی را انجام دهیم. برای تبدیل مقسوم به یک عدد صحیح، کافی است اعشار را دو رقم به سمت راست جابه‌جا کنیم. در واقع، با ضرب عدد ۱۰۰ در آن، این کار را انجام می‌دهیم. عدد مقسوم‌علیه را نیز با همین کار به یک عدد صحیح تبدیل می‌کنیم. با توجه به اینکه هم اعشار مقسوم و هم اعشار مقسوم‌علیه را دو رقم به سمت راست جابه‌جا کرده‌ایم، در پایان نیازی به تغییر جواب نیست. دلیل واضح‌تر این امر آن است که یک تقسیم داریم که هم مقسوم و هم مقسوم‌علیه را در عدد ۱۰۰ ضرب کرده‌ایم و به همین دلیل، اصل تقسیم تغییری نمی‌کند.
اکنون به سراغ تقسیم چکشی می‌رویم و 1275 را بر 11 تقسیم می‌کنیم. در این مثال، باید عدد چهار رقمی را بر عددی دو رقمی تقسیم کنیم. می‌خواهیم تقسیم 1275 بر 11 را انجام دهیم. ابتدا تقسیم را به‌شکل مناسب چکشی می‌نویسیم. برای شروع، ابتدا از چپ دو رقم را جدا می‌کنیم و بررسی می‌کنیم که این عدد دورقمی بزرگ‌تر از مقسوم‌علیه (عدد 11) باشد. می‌بینیم که 12 بزرگ‌تر از 11 است. در نتیجه، جدا کردن این دو رقم کافی است. حال این سؤال را از خودمان می‌پرسیم که «چند تا 11 در 12 وجود دارد؟» واضح است که ۱ تا 11 تایی در 12 قرار دارد. پس عدد ۱ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم.
حاصل‌ضرب ۱ در ۱۱ برابر با ۱۱ است. این عدد را از ۱۲ کم می‌کنیم و حاصل را که ۱ است، می‌نویسیم.
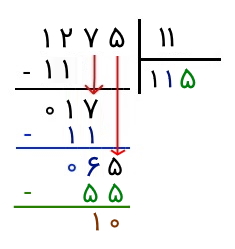
در مرحله بعد، می‌بینیم که نمی‌توان ۱ را بر ۱۱ تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین میآوریم و به عدد ۱۷ می‌رسیم که از ۱۱ بزرگ‌تر است و می‌توانیم آن را بر ۱۱ تقسیم کنیم. اکنون از خودمان می‌پرسیم که چند تا ۱۱ در ۱۷ می‌تواند قرار داشته باشد. جواب باز هم ۱ است. پس ۱ را در کنار ۱ قبلی در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در ۱۱ ضرب می‌کنیم و عدد حاصل (یعنی ۱۱) را زیر ۱۷ می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد ۶ است.
کار را مشابه مراحل قبل ادامه می‌دهیم. می‌بینیم که ۶ از ۱۱ کوچک‌تر است. پس یک رقم دیگر را پایین میآوریم و به عدد ۶۵ می‌رسیم. اکنون می‌توانیم ۶۵ را بر ۱۱ تقسیم کنیم. می‌بینیم که پنج ۱۱ تایی در ۶۵ می‌تواند وجود داشته باشد. پس رقم ۵ را در کنار دو رقم دیگر در خارج قسمت می‌نویسیم. پس از آنکه رقم ۵ را نوشتیم، آن را در ۱۱ ضرب می‌کنیم و حاصل را که برابر با ۵۵ است، زیر عدد ۶۵ یادداشت می‌کنیم. حال باید ۵۵ را از ۶۵ کم کنیم که حاصل آن می‌شود ۱۰. مشاهده می‌کنیم که ۱۰ از ۱۱ کوچک‌تر است و نمی‌توان آن را بر ۱۱ تقسیم کرد. رقمی هم از مقسوم اصلی باقی نمانده که آن را پایین بیاوریم. پس اینجا تقسیم خاتمه پیدا می‌کند.
مراحل انجام تقسیم در بالا نشان داده شده است.
بنابراین، برای تقسیم ۱۲۷۵ بر ۱۱، خارج‌قسمت ۱۱۵ و باقیمانده ۱۰ به‌دست آمد. اما نکته مهم در اینجا، باقیمانده است. دو رقم اعشار را باید بر باقیمانده اعمال کنیم. دقت کنید که باقیمانده باید حتماً از مقسوم‌علیه کوچک‌تر باشد.
پس، در نهایت، می‌توان گفت برای تقسیم ۱۲٫۷۵ بر ۰٫۱۱، خارج‌قسمت برابر با ۱۱۵ و باقیمانده ۰٫۱ است.
مثال چهارم نمونه سوال تقسیم چکشی
عدد ۲۳۸ را بر ۸ تقسیم کنید.
جواب: همان‌طور که می‌بینیم، مقسوم سه رقم دارد و مقسوم‌علیه داری یک رقم است. مشاهده می‌کنیم که با انتخاب یک رقم از سمت چپ از عدد ۲۳۸، عمل تقسیم بر ۸ امکان‌پذیر نیست. بنابراین دو رقم را جدا می‌کنیم که عدد ۲۳ است. می‌دانیم که ۲۳ تقسیم بر ۸، خارج‌قسمتی برابر با ۲ و باقیمانده‌ای برابر با ۷ خواهد داشت.
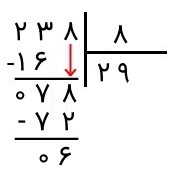
عدد ۷ کوچک‌تر از ۸ است و باید رقم ۸ بالا را پایین بیاوریم. پس به عدد ۷۸ می‌رسیم. اکنون ۷۸ را بر ۸ تقسیم می‌کنیم که حاصلش عدد ۹ است. ضرب این عدد در مقسوم‌علیه برابر با ۷۲ است. آن را زیر ۷۸ می‌نویسیم و از آن کم می‌کنیم. پس، باقیمانده برابر با ۶ است.
مثال پنجم نمونه سوال تقسیم چکشی
حاصل تقسیم عدد ۶۰۹۰ بر ۸۸ را به‌دست آورید.
جواب: ابتد دو رقم از چپ جدا می‌کنیم که چون 60 از 88 کوچک‌تر است، کافی نیست. پس یک رقم دیگر نیز جدا می‌کنیم. اکنون 609 از 88 بزرگ‌تر است. اکنون این سؤال را از خودمان می‌پرسیم که «چند تا 88 در 609 وجود دارد؟» می‌بینیم که 6 تا 88 تایی در 609 قرار دارد. بنابراین، عدد 6 را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم. حاصل‌ضرب 6 در 88 برابر با 528 است. این عدد را از 609 کم می‌کنیم و حاصل را می‌نویسیم.
در مرحله بعد، می‌بینیم که نمی‌توان 81 را بر 88 تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین میآوریم و به عدد 810 می‌رسیم که از 88 بزرگ‌تر است و می‌توانیم آن را بر 88 تقسیم کنیم. اکنون از خودمان می‌پرسیم که چند تا 88 در 810 می‌تواند قرار داشته باشد. جواب 9 است. پس 9 را در کنار 6 در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در 88 ضرب می‌کنیم و عدد حاصل (یعنی 792) را زیر 810 می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد 18 است.
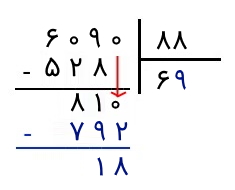
مشاهده می‌کنیم که 18 از 88 کوچک‌تر است و نمی‌توان آن را بر 88 تقسیم کرد. رقمی هم از مقسوم اصلی باقی نمانده که آن را پایین بیاوریم. پس اینجا تقسیم خاتمه پیدا می‌کند.
مثال ششم نمونه سوال تقسیم چکشی
عدد ۳۵٫۲۴ را بر ۰٫۳۲ تقسیم کنید.
جواب: می‌بینیم که دو عدد اعشاری هستند. ساده‌ترین کار این است که این دو عدد را به اعدادی صحیح تبدیل کنیم، سپس تقسیم چکشی را انجام دهیم. برای تبدیل مقسوم به یک عدد صحیح، کافی است اعشار را دو رقم به سمت راست جابه‌جا کنیم. در واقع، با ضرب عدد ۱۰۰ در آن، این کار را انجام می‌دهیم. عدد مقسوم‌علیه را نیز با همین کار به یک عدد صحیح تبدیل می‌کنیم. با توجه به اینکه هم اعشار مقسوم و هم اعشار مقسوم‌علیه را دو رقم به سمت راست جابه‌جا کرده‌ایم، در پایان نیازی به تغییر جواب نیست. دلیل واضح‌تر این امر آن است که یک تقسیم داریم که هم مقسوم و هم مقسوم‌علیه را در عدد ۱۰۰ ضرب کرده‌ایم و به همین دلیل، اصل تقسیم تغییری نمی‌کند.
اکنون به سراغ تقسیم چکشی می‌رویم و ۳۵۲۴ را بر ۳۲ تقسیم می‌کنیم. در این مثال، باید عدد چهار رقمی را بر عددی دو رقمی تقسیم کنیم. می‌خواهیم تقسیم ۳۵۲۴ بر ۳۲ را انجام دهیم. ابتدا تقسیم را به‌شکل مناسب چکشی می‌نویسیم. برای شروع، ابتدا از چپ دو رقم را جدا می‌کنیم و بررسی می‌کنیم که این عدد دورقمی بزرگ‌تر از مقسوم‌علیه (عدد ۳۲) باشد. می‌بینیم که ۳۵ بزرگ‌تر از ۳۲ است. در نتیجه، جدا کردن این دو رقم کافی است. حال این سؤال را از خودمان می‌پرسیم که «چند تا ۳۲ در ۳۵ وجود دارد؟» می‌بینیم که ۱ تا ۳۲ تایی در ۳۵ قرار دارد. پس عدد ۱ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم.
حاصل‌ضرب ۱ در ۳۲ برابر با ۳۲ است. این عدد را از ۳۵ کم می‌کنیم و حاصل را که ۳ است، می‌نویسیم.
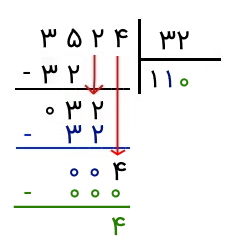
در مرحله بعد، می‌بینیم که نمی‌توان ۳ را بر ۳۲ تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین میآوریم و به عدد ۳۲ می‌رسیم که برابر با ۳۲ است. و می‌توانیم آن را بر ۳۲ تقسیم کنیم. اکنون از خودمان می‌پرسیم که چند تا ۳۲ در ۳۲ می‌تواند قرار داشته باشد. جواب باز هم ۱ است. پس ۱ را در کنار ۱ قبلی در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در ۳۲ ضرب می‌کنیم و عدد حاصل (یعنی ۳۲) را زیر ۳۲ می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد ۰ است.
اکنون ۴ را پایین میآوریم. می‌بینیم که ۴ کوچک‌تر از ۳۲ است. پس هیچ ۳۲ تایی در آن جای نمی‌گیرد. در نتیجه، کافی است رقم ۰ را در خارج قسمت بنویسیم. حاصل‌ضرب آن در ۳۲ نیز برابر با صفر است و زیر ۴ آن را می‌نویسیم و از آن کم می‌کنیم. پس خارج قسمت برابر با ۱۱۰ و باقیمانده برابر با ۴ است.
بنابراین، برای تقسیم ۳۵۲۴ بر ۳۲، خارج‌قسمت ۱۱۰ و باقیمانده ۴ به‌دست آمد. اما نکته مهم در اینجا، باقیمانده است. دو رقم اعشار را باید بر باقیمانده اعمال کنیم. دقت کنید که باقیمانده باید حتماً از مقسوم‌علیه کوچک‌تر باشد.
پس، در نهایت، می‌توان گفت برای تقسیم ۳۵٫۲۴ بر ۰٫۳۲، خارج‌قسمت برابر با ۱۱۰ و باقیمانده ۰٫۰۴ است.
