نفوذپذیری مغناطیسی – به زبان ساده
در آموزشهای قبلی مجله فرادرس درباره گذردهی الکتریکی صحبت کردیم. در این آموزش قصد داریم «نفوذپذیری مغناطیسی» (Permeability) را بررسی کنیم. مواد مغناطیسی موادی هستند که وقتی در معرض یک میدان مغناطیسی قرار میگیرند، از خود «قطبیت مغناطیسی» (Magnetic Polarization) نشان میدهند.

ممان مغناطیسی
همانطور که گفتیم اعمال میدان مغناطیسی به مواد مغناطیسی، باعث ایجاد «قطبیت مغناطیسی» (Magnetic Polarization) در این مواد میشود. قطبیت مغناطیسی منجر به همجهت شدن دوقطبیهای مغناطیسی ماده با میدان مغناطیسی اعمالی میشود. به این پدیده، «مغناطش» (Magnetization) گویند. این پدیده همانند آرایش دوقطبیهای الکتریکی در میدان الکتریکی خارجی است.
پیشبینی رفتار مواد مغناطیسی هنگامی که در معرض میدان مغناطیسی خارجی قرار میگیرند، تنها توسط «نظریه کوانتم» (Quantum Theory) قابل توضیح است. این نظریه برای کاربردهای مهندسی، معمولا بسیار پیچیده و غیرعملی است. هرچند با استفاده از مدلهای ساده اتمی که ساختار شبکه اتمی ماده را نشان میدهند، نتایج کمّی مناسبی حاصل میشود. مطابق این مدلهای اتمی، الکترونها که حامل بار منفی هستند به دور هسته حامل بار مثبت میچرخند. در مبحث حل مسائل مغناطیس ساکن، درباره جریان ساکن و دو قطبی مغناطیسی صحبت کردیم. حرکت دایرهای الکترون به دور هسته یک جریان الکتریکی ساکن ایجاد میکند. بنابراین میتوان این جریان را با یک دوقطبی مغناطیسی مدل کرد شکل زیر مدل اتمی یک ماده و معادلهای آن را که نمایانگر ساختار شبکه اتمی ماده مغناطیسی است، نشان میدهد:
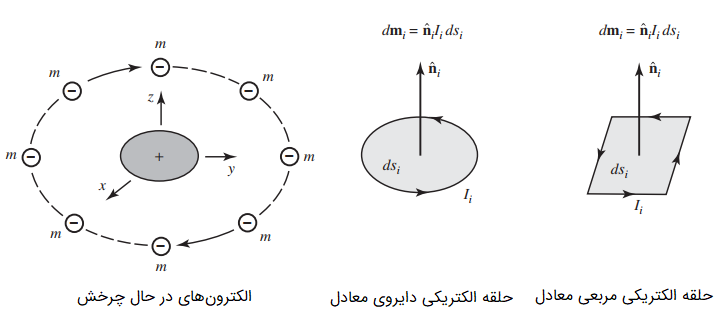
هر الکترون در حال چرخش را میتوان به صورت یک حلقه کوچک جریان الکتریکی با مساحت مدل کرد. جریان در این حالتِ معادل، خلاف جهت چرخش الکترون است. مادامی که حلقه بسیار کوچک است، میتواند به شکل دایره، مربع یا هر چیز دیگری باشد. همانطور که در شکل (۱) مشاهده میشود، میتوان حلقه را به صورت مربعی نیز در نظر گرفت. میدان ایجاد شده در فاصله دور به وسیله حلقه کوچک حامل جریان الکتریکی با میدان ایجاد شده توسط یک آهنربای میلهای خطی (دوقطبی مغناطیسی) با طول برابر است.
مطابق شکل (۱)، «تکانه زاویهای» (Angular Momentum) مربوط به یک الکترون در حال چرخش را میتوان به وسیله ممان دوقطبی مغناطیسی نشان داد. این ممان به صورت زیر تعریف میشود:
معادله (۱)
برای اتمهایی که الکترونهای در حال چرخش بسیاری دارند، ممان دوقطبی مغناطیسی کل برابر با جمع برداری همه ممانهای دوقطبی مغناطیسی است. هر کدام از این ممانهای دوقطبی به وسیله معادله (۱) داده میشود. بنابراین میتوان نوشت:
معادله (۲)
در این معادله، با تعداد کل الکترونهای در حال چرخش (حلقههای معادل) بر حسب واحد حجم برابر است. بردار قطبیت مغناطیسی یا «مغناطش» (Magnetization) با نماد نشان داده میشود و تعریف آن به صورت زیر است:
معادله (۳)
فرض کنید ممان مغناطیسی متوسط برای هر حلقه به صورت زیر است:
معادله (۴)
حال اگر فرض کنیم همه حلقهها موازی هم هستند، بردار قطبیت مغناطیسی در معادله (۳) را میتوان به صورت زیر بازنویسی کرد:
معادله (۵)
یک ماده مغناطیسی به وسیله تعداد دوقطبیها و ممانهای مغناطیسی آن شناخته میشود. در غیاب میدان مغناطیسی خارجی، دوقطبیهای مغناطیسی و حلقههای الکتریکی معادل، جهات تصادفی دارند. بنابراین در مقیاس ماکروسکوپی، جمع برداری ممانهای مغناطیسی در معادله (۳) و قطبیت مغناطیسی در معادله (۴) برابر صفر هستند. جهتگیری تصادفی دوقطبیهای مغناطیسی و حلقهها در شکل زیر نشان داده شده است:
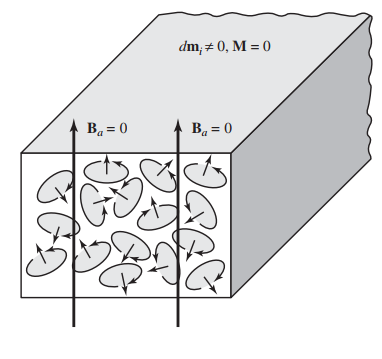
هنگامی که یک میدان با چگالی شار مغناطیسی به ماده مغناطیسی اعمال میشود، بیشتر دوقطبیهای مغناطیسی ماده با میدان مغناطیسی همجهت میشوند. شکل زیر این مسئله را نشان میدهد:
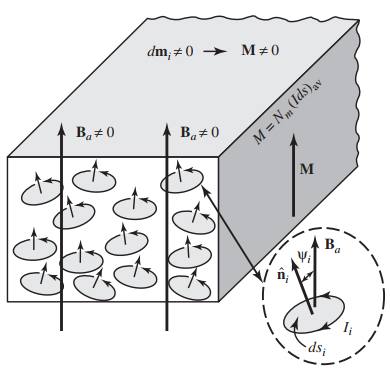
بنابراین «گشتاور مغناطیسی» (Magnetic Torque) به صورت زیر نوشته میشود:
معادله (6)
این گشتاور بر حسب همه ممانهای دوقطبی مغناطیسی نوشته شده است. شکل (۳) این گشتاور را نشان میدهد. به طور ایدهآل، اگر هیچ ممان مغناطیسی دیگری وجود نداشته باشد، میتوان از رابطه (۶) برای محاسبه گشتاور استفاده کرد. این گشتاور تا زمانی وجود دارد که هر یک از الکترونهای چرخان به گونهای جابجا شود که میدان مغناطیسی ایجاد شده به وسیله حلقه الکتریکی (یا ممان مغناطیسی) معادل آن با میدان اعمالی همجهت شود. بنابراین میدان مغناطیسی منتجه در هر نقطه داخل ماده از حالتی که ماده مغناطیسی وجود ندارد، بزرگتر است.
نفوذپذیری مغناطیسی
حال یک ماده مغناطیسی را در نظر بگیرید. فرض کنید که یک میدان مغناطیسی با چگالی شار به این ماده اعمال شود.
بردار مغناطش ناشی از جهتگیری مجدد دوقطبیهای مغناطیسی داخل ماده مغناطیسی، در شکل زیر نشان داده شده است:
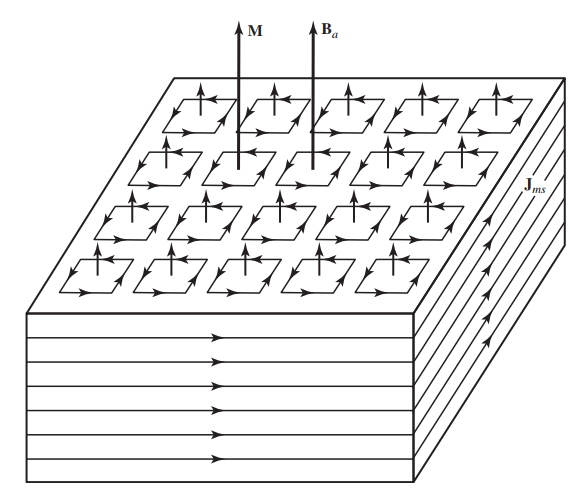
به طور ایدهآل، در مقیاس میکروسکوپی برای بیشتر مواد مغناطیسی همه دوقطبیهای مغناطیسی همجهت میشوند و به این ترتیب، ممان مغناطیسی همه دوقطبیها با میدان مغناطیسی اعمالی همجهت میشوند. این مسئله در شکل (۴) نشان داده شده است. در حد که تعداد دوقطبیهای مغناطیسی و حلقههای الکتریکی معادل بسیار بزرگ میشوند، جریان حلقهها در قسمتهای داخلی تیغه مغناطیسی به وسیلههای حلقههای مجاور خنثی میشود. در مقیاس ماکروسکوپی، جریان مغناطیسی معادل خالص غیر صفر میشود. این مسئله منجر به ایجاد چگالی جریان سطحی مغناطیسی معادل با واحد آمپر بر متر میشود. این جریان روی سطحی خارجی تیغه یافت میشود. چگالی جریان مغناطیسی معادل با نماد نشان داده میشود و مسئول همجهت شدن بردار مغناطش با جهت میدان مغناطیسی است.
چگالی شار مغناطیسی در طول تیغه به دلیل حضور افزایش مییابد. بنابراین چگالی شار مغناطیسی در هر نقطه داخل تیغه مغناطیسی با رابطه زیر داده میشود:
معادله (7)
ذکر این نکته ضروری است که واحد در معادله (۳) آمپر بر متر است و به شدت میدان مغناطیسی وابسته است. در حالت کلی، میتوان چگالی شار مغناطیسی را به میدان مغناطیسی به وسیله پارامتر طراحی شده مرتبط دانست. واحد این پارامتر هانری بر متر است. پس میتوان نوشت:
معادله (۸)
مقایسه معادلههای (۷) و (۸)، نشان میدهد که نیز با با رابطه زیر مرتبط است:
معادله (۹)
در این معادله، «حساسیت مغناطیسی» (Magnetic Susciptibility) نام دارد و بدون واحد است. با جایگزینی معادله (۹) در معادله (۷) و استفاده از آن در معادله (۸) خواهیم داشت:
معادله (۱۰)
پس میتوان معادله زیر را نوشت:
معادله (۱۱)
در معادله (۱۱)، ، «نفوذپذیری مغناطیسی استاتیک» (Static Permeability) برای محیط است. مقدار نسبی نسبت به فضای آزاد () به صورت زیر تعریف میشود:
معادله (۱۲)
جریان مغناطیسی معادل
در داخل ماده، چگالی جریان مغناطیسی محدود القا میشود و با بردار قطبیت مغناطیسی به صورت زیر مرتبط است:
معادله (۱۳)
برای محاسبه این چگالی جریان، قانون آمپری ماکسول را به صورت زیر بازنویسی میکنیم:
معادله (14)
روی سطح ماده، چگالی جریان سطحی مغناطش محدود با بردار قطبیت مغناطیسی در سطح به صورت زیر رابطه دارد:
$$\Large J_{ms} = M \times \hat n\Bigr{|}_{surface} (\mathrm{A/m})$$
در معادله (15)، بردار نرمال واحد در سطح ماده است. جریان مغناطش محدود از سطح مقطع ماده عبور میکند و میتوان آن را بر حسب معادله زیر پیدا کرد:
معادله (۱۶)
الکترونها علاوه بر چرخش به دور هسته اتم، حول محور خود نیز چرخش میکنند که «اسپین» (Spin) نام دارد. بنابراین یک ممان مغناطیسی به اندازه وجود دارد که مربوط به حرکت اسپینی الکترونهاست. این ممان با میدان مغناطیسی اعمالی، مخالفت میکند یا آن را تقویت میکند. علامت مثبت نشاندهنده تقویت میدان و علامت منفی نشاندهنده مخالفت با آن است. برای اتمهایی که در لایههای خود الکترونهای متعددی دارند، تنها اسپین مربوط به الکترونها در لایههایی که کاملا پر نشدهاند، در ممان مغناطیسی اتمها نقش دارند. سومین عامل ایجاد ممان مغناطیسی کلی در یک اتم، حرکت اسپینی هسته اتم است. که «اسپین هستهای» (Nuclear Spin) نام دارد. هرچند، ممان مغناطیسی اسپین هستهای (که مقداری در حدود دارد) نسبت به ممان اسپین الکترون و ممان چرخش الکترون به دور هسته بسیار کوچکتر است. در ادامه با بیان یک مثال، به بررسی بیشتر نفوذپذیری مغناطیسی میپردازیم.
مثال
یک شمش از جنس ماده مغناطیسی با طول محدود و در جهت را در نظر بگیرید. شکل زیر این شمش را نشان میدهد:
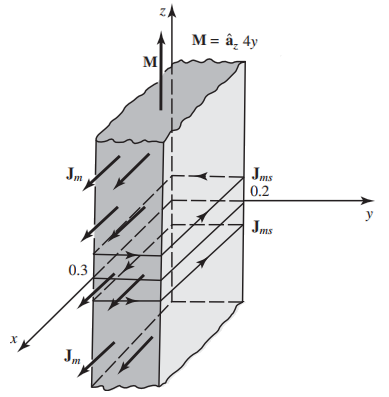
یک میدان مغناطیسی به این شمش مغناطیسی اعمال میشود، به طوری که بردار مغناطش در هر نقطه داخل شمش به صورت زیر است:
چگالی جریان حجمی و چگالی جریان سطحی روی هر چهار سطح و همچنین جریان کلی گذرنده از شمش به موازات محور و روی صفحه بیابید.
حل: با استفاده از معادله (۱۳) داریم:
با استفاده از معادله (۱۴) داریم:
بنابراین:
در صفحه داریم:
در صفحه داریم:
در صفحه داریم:
و در صفحه :
جریان گذرنده از سطح به صورت زیر محاسبه میشود:
انواع مختلف مواد از نظر مغناطیسی
همانند گذردهی الکتریکی نسبی، نفوذپذیری مغناطیسی () و نفوذپذیری مغناطیسی نسبی () توابعی از فرکانس هستند. مقادیر نفوذپذیری مغناطیسی که در جدول نشان داده شدند، مربوط به فرکانسهایی هستند که میدانهای ساکن یا شبهساکن دارند.
مطابق جدول، واضح است که به غیر از مواد فرومغناطیس، مقدار ضریب نفوذپذیری مغناطیسی برای بیشتر مواد در حدود واحد است. بنابراین برای مسائل مهندسی، معمولا مقدار واحد در نظر گرفته میشود. مقادیر استاتیک برای چند ماده در جدول زیر آورده شده است:
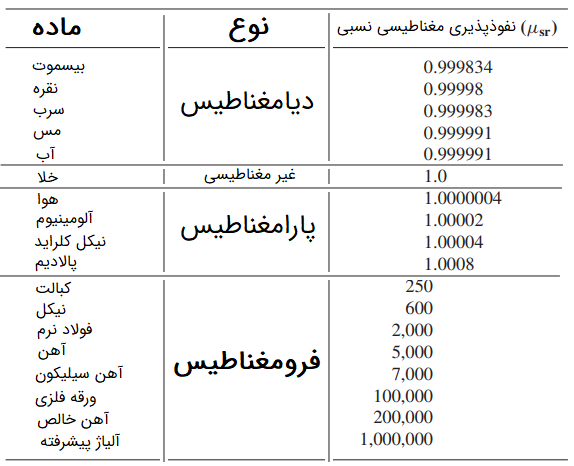
بردار مغناطش کلی برای مواد گروه دوم، میدان مغناطیسی اعمالی را بهبود میدهد و همجهت با آن است. بنابراین در این گروه، نفوذپذیری مغناطیسی نسبی، مقداری بزرگتر از یک دارد. برای بعضی از این مواد، (پارامغناطیس و ضد فرومغناطیس)، مقدار نفوذپذیری مغناطیسی کمی بزرگتر از واحد است (). در حالی که نفوذپذیری مغناطیسی برای بقیه مواد (فرّومغناطیس و فرّی مغناطیس)، مقداری بسیار بزرگتر از یک دارد ().
در غیاب میدان مغناطیسی خارجی، ممان ناشی از حرکت اسپینی الکترونها در مواد دیامغناطیس با یکدیگر و با ممان مربوط به چرخش الکترونها به دور هسته مخالفت میکند. به این ترتیب، در مقایس ماکروسکوپی ممان مغناطیسی کلی () برابر صفر خواهد بود.
در حضور میدان مغناطیسی خارجی، ممان مغناطیسی هر اتم غیر صفر خواهد بود. در مقیاس ماکروسکوپی، ممان مغناطیسی همه اتمها به بردار مغناطش کلی منجر میشود. برای ماده دیامغناطیس، بردار اندازهای بسیار کوچک دارد و با میدان مغناطیسی اعمالی مخالفت میکند. به این ترتیب، حساسیت مغناطیسی منفی میشود و مقدار نفوذپذیری مغناطیسی نسبی، کمی کوچکتر از یک خواهد بود. برای مثال، فلز مس یک ماده دیامغناطیس با حساسیت مغناطیسی و نفوذپذیری مغناطیسی نسبی تقریبی است.
برای مواد پارامغناطیس در غیاب میدان مغناطیسی خارجی، ممان مغناطیسی مربوط به چرخش الکترونها به دور هسته و ممان ناشی از حرکت اسپینی الکترون در اتم، اثرات یکدیگر را خنثی نمیکنند. بنابراین اتمهای مواد پارامغناطیس، مقدار کوچکی ممان یا گشتاور مغناطیسی خواهد داشت. هرچند، به دلیل جهتگیری تصادفی ممان مغناطیسی هر اتم در غیاب میدان مغناطیسی خارجی، ممان مغناطیسی کل دوقطبیها برای یک نمونه بزرگ (از نظر ماکروسکوپی) از ماده و بردار مغناطش برابر صفر خواهد بود.
هنگامی که یک میدان مغناطیسی به ماده پارامغناطیس اعمال میشود، تعداد کمی از دوقطبیهای مغناطیسی با میدان اعمالی همجهت میشوند. به این ترتیب، یک بردار کوچک غیر صفر همجهت با میدان مغناطیسی اعمالی ایجاد میشود. به این ترتیب، چگالی شار مغناطیسی داخل ماده افزایش مییابد. بنابراین حساسیت مغناطیسی مقدار مثبت کوچکی خواهد داشت و مقدار نفوذپذیری مغناطیسی نسبی کمی بزرگتر از یک خواهد شد. برای مثال، حساسیت مغناطیسی فلز آلومینیوم معادل و نفوذپذیری مغناطیسی نسبی آن در حدود است.

اتمهای مواد فرّومغناطیس در غیاب میدان مغناطیسی خارجی، ممانهای مغناطیسی بسیار قوی دارد. این ممانها معمولا از حرکت اسپینی الکترونها ناشی میشوند. در مواد فرومغناطیس، ممان مغناطیسی تعدادی اتم (مثلا پنج یا شش اتم) یکدیگر را تقویت میکنند و نواحی مختلفی به نام «حوزه مغناطیسی» (Magnetic Domains) را ایجاد میکنند. این حوزهها میتوانند شکل و اندازههای مختلفی داشته باشند. ابعاد حوزه به حالت و تاریخچه مغناطیسی قبلی ماده بستگی دارد و میتواند از تا چند میلیمتر باشد. در مقیاس ماکروسکوپی، بردار مغناطش خالص در غیاب میدان مغناطیسی خارجی صفر است، زیرا حوزهها جهتگیری تصادفی دارند و ممانهای مغناطیسی اتمهای مختلف، اثر یکدیگر را خنثی میکنند.
با اعمال یک میدان مغناطیسی به ماده فرّومغناطیسی، علاوه بر ممان مغناطیسی بسیار بزرگ مربوط به خود اتمها، بردار مغناطش نیز اندازه بزرگی خواهد داشت. به این ترتیب، جمع برداری این دو ممان، مقدار بسیار بزرگی خواهد داشت. این مسئله باعث میشود حساسیت مغناطیسی و نفوذپذیری مغناطیسی ماده اعداد بسیار بزرگی شوند. در جدول، اعداد معمول برای نفوذپذیری مغناطیسی () چند ماده فرومغناطیس آورده شده است.
هنگامی که میدان مغناطیسی خارجی از بین میرود، آرایش ممان مغناطیسی اتمهای مختلف مجددا تصادفی نمیشود و یک ممان مغناطیسی یا پسماند مغناطیسی غیر صفر باقی میماند. از آنجا که ممان مغناطیسی ماده فرومغناطیس در مقیاس ماکروسکوپی بعد از حذف میدان مغناطیسی با قبل از حذف متفاوت است، حالت مغناطیسی ماده به تاریخچه آن بستگی دارد. به همین دلیل، رسم منحنی چگالی شار مغناطیسی نسبت به میدان مغناطیسی منجر به ایجاد حلقه هیسترزیس میشود. مواد با این خاصیت برای طراحی ترانسفورماتورها، هستههای القایی و ضبط مغناطیسی بسیار مناسب هستند.
در گروه دیگری از مواد، شدت ممان مغناطیسی هر اتم بالاست. اما از دید ماکروسکوپی، بردار ممان اتمها اندازهای مشابه دارند و جهت آنها مخالف یکدیگر است. به این ترتیب، ممان مغناطیسی کلی در غیاب میدان مغناطیسی خارجی صفر میشود. این مواد، «ضد فرومغناطیس» (AntiFerromagnetic) نام دارند. حضور میدان مغناطیسی خارجی، اثر کمی روی این مواد دارد. به این ترتیب، نفوذپذیری مغناطیسی این مواد کمی بزرگتر از یک است.
در گروه دیگری از مواد، شدت ممان مغناطیسی اتمهای مجاور هم در یک ماده اندازه خیلی بزرگی دارند اما در غیاب میدان مغناطیسی خارجی، این ممانها اندازههای مختلفی خواهند داشت. این مواد، «فرّی مغناطیس» (Ferrimagnetic) نامیده میشود. حضور میدان مغناطیسی خارجی، بر این مواد بسیار تاثیرگذار است و به نفوذپذیری مغناطیسی بسیار بزرگی منجر میشود. البته این نفوذپذیری به اندازه مواد فرّومغناطیس بزرگ نیست.
«فریتها» (Ferrite) گروهی از مواد فرومغناطیسی هستند که هدایت بسیار کمی دارند (خیلی خیلی کمتر از نیمههادیها). هنگامی که این مواد در معرض میدانهای متناوب قرار میگیرند، به دلیل مقاومت بسیار بزرگ در این مواد، جریانهای کوچکتری در آنها القا میشود که منجر به تلفات اهمی کمتر میشود. این نوع مواد در طراحی دستگاههای مایکروویو غیر همپاسخ از قبیل ایزولاتورها، هایبریدها، ژیراتورها و تغییردهندههای فاز و غیره کاربردهای بسیاری دارند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- امواج الکترومغناطیسی — از صفر تا صد
- میدان مغناطیسی جریان — از صفر تا صد
- مغناطیس چیست؟ — به زبان ساده
^^












بسیار عالی بود..
آیا نمیشود که از مطالب نسخه ای داشته اشیم؟