مقیاس دمای ترمودینامیکی – به زبان ساده

هنگامی که مقیاس دما به ویژگی‌های ماده‌ای که برای اندازه‌گیری دما مورد استفاده قرار می‌گیرد، وابسته نباشد، مقیاس دمای ترمودینامیکی (Thermodynamic Temperature Scale)‌ نامیده می‌شود. مقیاس دمای ترمودینامیکی برای محاسبات ترمودینامیکی مناسب است و برای استخراج آن می‌توانیم از چند موتور گرمایی برگشت‌پذیر کمک بگیریم.

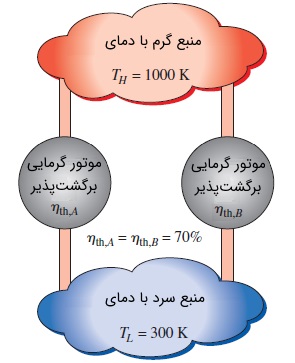
قبلاً در مجله فرادرس و به عنوان دومین قضیه کارنو گفته بودیم تمام موتورهای گرمایی برگشت‌پذیر که بین دو منبع دمای یکسان کار می‌کنند،‌ دارای راندمان حرارتی برابری هستند. به عبارت دیگر، راندمان یک موتور حرارتی برگشت‌پذیر، به سیال کاری و ویژگی‌های آن، نحوه کامل شدن چرخه و حتی نوع ماشین برگشت‌پذیر وابسته نیست. از آنجایی که مشخصه منابع حرارتی، دمای آنهاست و با توجه به رابطه $$\large \eta_ {\text {th}} =1 -Q_L /Q_H$$،‌ راندمان حرارتی موتورهای گرمایی را می‌توان به عنوان تابعی از دمای منابع حرارتی مرتبط با آنها نوشت. رابطه زیر را در نظر بگیرید.

$$\large \eta_ {\text {th, rev}} \:=\: g(T_H,\: T_L) \\~\\ \large \frac {Q_H} {Q_L} \:=\: f(T_H, \:T_L)$$

(رابطه ۱)

در رابطه‌های بالا، پارامترهای $$\large T_H$$ و $$\large T_L$$، به ترتیب دمای مربوط به منبع حرارتی گرم و سرد را نشان می‌دهند. شکل تابع $$\large f(T_H, \:T_L)$$ را می‌توانیم با کمک سه موتور گرمایی برگشت‌پذیر نشان داده شده در شکل زیر توسعه دهیم. مقدار گرمای یکسان $$\large Q_1$$ از طریق منبع حرارتی گرم با دمای $$\large T_1$$، به هر دو موتور $$\large \text {A}$$ و $$\large \text {C}$$ وارد شده است. موتور $$\large \text {C}$$، گرمای $$\large Q_3$$ را به منبع حرارتی سرد با دمای $$\large T_3$$ می‌دهد. اما موتور $$\large \text {A}$$، گرمای $$\large Q_2$$ را در دمای $$\large T_2$$ به موتور $$\large \text {B}$$ داده و موتور $$\large \text {B}$$ نیز گرمای $$\large Q_3$$ را به منبع حرارتی سرد با دمای $$\large T_3$$ منتقل می‌کند.

فیلم آموزش ترمودینامیک ۲ – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

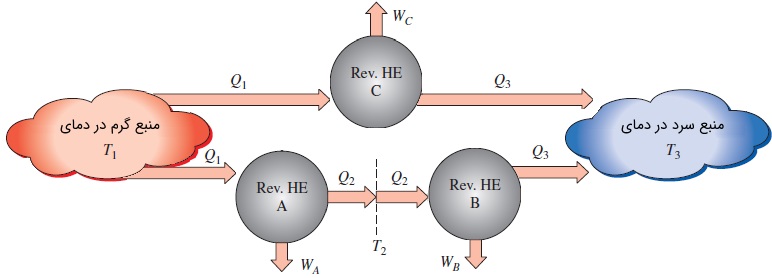
مقدار گرمای دفع شده توسط موتورهای $$\large \text {B}$$ و $$\large \text {C}$$ باید یکسان باشد. زیرا می‌توانیم موتورهای گرمایی $$\large \text {A}$$ و $$\large \text {B}$$ را در قالب یک موتور گرمایی واحد، با یکدیگر ادغام کنیم تا مانند موتور گرمایی $$\large \text {C}$$ بین دو منبع گرمایی گرم و سرد کار کند. در نتیجه، راندمان موتور گرمایی ادغام شده با موتور $$\large \text {C}$$ برابر خواهد بود. از آنجایی که مقدار انرژی گرمایی دریافتی توسط هر دو موتور (موتور $$\large \text {C}$$ و موتور ادغام شده $$\large \text {A}$$ و $$\large \text {B}$$) یکسان است، مقدار گرمای دفع شده توسط آنها نیز برابر خواهد بود. رابطه ۱ را برای هر سه موتور می‌نویسیم.

$$\large \frac {Q_1} {Q_2} \:=\: f(T_1, \:T_2) \\~\\ \large \frac {Q_2} {Q_3} \:=\: f(T_2, \:T_3) \\~\\ \large \frac {Q_1} {Q_3} \:=\: f(T_1, \:T_3)$$

(رابطه ۲)

استفاده از تناسب $$\large \frac {Q_1} {Q_3}= \frac {Q_1} {Q_2} \times \frac {Q_2} {Q_3}$$، رابطه ۲ را به شکل زیر تبدیل می‌کند.

$$\large f(T_1,\: T_3) \:=\: f(T_1,\: T_2) \times f(T_2,\: T_3)$$

با دقت در رابطه بالا در می‌یابیم که چون قسمت سمت چپ رابطه، تابعی از $$\large T_1$$ و $$\large T_3$$ است، قسمت سمت راست هم باید تابعی از $$\large T_1$$ و $$\large T_3$$ و مستقل از $$\large T_2$$‌ باشد. این وضعیت فقط در صورتی برآورده خواهد شد که تابع $$\large f$$ به شکل کلی زیر باشد.

$$\large f(T_1,\: T_2) \:=\: \frac {\phi (T_1)} {\phi (T_2)} \\~\\ \large f(T_2,\: T_3) \:=\: \frac {\phi (T_2)} {\phi (T_3)}$$

از این رو، در حاصل‌ضرب دو تابع $$\large f(T_1,\: T_2)$$ و $$\large f(T_2,\: T_3)$$، عبارت $$\large \phi (T_2)$$ از طرفین ساده شده و رابطه زیر برقرار خواهد بود.

$$\large \frac {Q_1} {Q_3} \:=\: f(T_1, \:T_3) \:=\: \frac {\phi (T_1)} {\phi (T_3)}$$

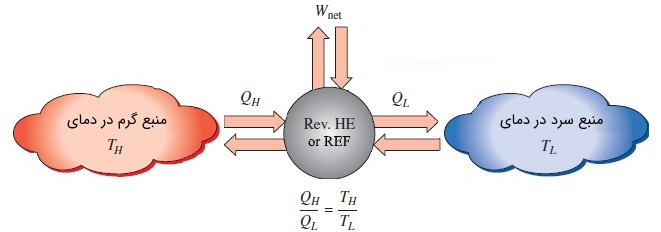
رابطه بالا،‌ برای نشان دادن اینکه $$\large \frac {Q_1} {Q_3}$$ تابعی از $$\large T_1$$ و $$\large T_3$$ است، جزئیات بیشتری نسبت به رابطه ۱ ارائه می‌کند. اکنون می‌توانیم برای یک موتور گرمایی برگشت‌پذیر که بین دو منبع با دماهای $$\large T_H$$ و $$\large T_L$$ کار می‌کند، رابطه زیر را بنویسیم.

$$\large \frac {Q_H} {Q_L} \:=\: \frac {\phi (T_H)} {\phi (T_L)}$$

(رابطه ۳)

براساس قانون دوم ترمودینامیک،‌ تنها شرط لازم برای نسبت انتقال حرارت بین موتورهای گرمایی برگشت‌پذیر و منبع حرارتی، به صورت رابطه بالا است. توابع مختلفی وجود دارند که در رابطه ۳ صدق می‌کنند. اولین بار «لرد کلوین» (Lord Kelvin) پیشنهاد کرد که با تعریف $$\large \phi (T) =T$$، مقیاس دمای ترمودینامیکی به صورت زیر نوشته شود.

$$\large \left( \frac {Q_H} {Q_L} \right) _{\text {rev}} \:=\: \frac {T_H} {T_L}$$

(رابطه ۴)

این مقیاس دمای ترمودینامیکی به عنوان مقیاس کلوین شناخته می‌شود و دما در این مقیاس، دمای مطلق (Absolute Temperature) نامیده می‌شود. در مقیاس کلوین، نسبت‌های دما به نسبت انتقال حرارت بین موتورهای گرمایی برگشت‌پذیر و منابع حرارتی بستگی دارد و از ویژگی‌های فیزیکی هر ماده مستقل است. بازه تغییرات دما در این مقیاس دمای ترمودینامیکی از صفر تا بی‌نهایت است.

رابطه ۴ نمی‌تواند مقیاس دمای ترمودینامیکی را به طور کامل تعریف کند؛ زیرا فقط نسبتی از دماهای مطلق ارائه می‌کند. از سوی دیگر، باید بدانیم هر یک کلوین چقدر است. در کنفرانس بین‌المللی اوزان و مقیاس‌ها که در سال ۱۹۵۴ میلادی برگزار شد، نقطه سه‌گانه آب (حالتی که هر سه فاز آب با هم در تعادل هستند)، به آب در دمای $$\large 273.16\: \text {K}$$ اختصاص داده شد. مقدار هر کلوین به صورت $$\large \frac {1} {273.16}$$ از بازه دمایی بین صفر مطلق و دمای نقطه سه‌گانه آب تعریف می‌شود. مقدار واحد دما در مقیاس‌های کلوین و درجه سلسیوس، مشابه یکدیگر هستند ($$\large 1\: \text {K} \equiv 1\: ^\circ \text {C}$$

$$\large T (^\circ \text {C}) \:=\: T (\text {K}) \:-\: 273.15$$

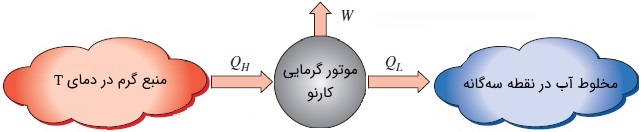
با وجود اینکه مقیاس دمای ترمودینامیکی با کمک موتورهای گرمایی برگشت‌پذیر تعریف شد، نه ممکن و نه حتی عملی است که چنین موتوری را راه‌اندازی کنیم تا مقادیر عددی مقیاس دمای ترمودینامیکی تعیین شود. برای اندازه‌گیری دماهای مطلق با دقت بالا، می‌توان از روش‌های دیگری هم استفاده کرد. استفاده از یک دماسنج گاز ایده‌آل در حجم ثابت به همراه بهره‌گیری از روش برون‌یابی، یکی از این روش‌هاست. در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• آموزش ترمودینامیک 2
• ترمودینامیک — از صفر تا صد
• قضیه کارنو - به زبان ساده
• فرآیند احتراق یا سوختن — از صفر تا صد
• تعریف گرما و دما در ترمودینامیک — به زبان ساده