محاسبه میدان الکتریکی — به زبان ساده

در مقاله «میدان الکتریکی (Electric Field) چیست؟ — از صفر تا صد» با مفهوم میدان الکتریکی آشنا شدیم. در این مقاله قصد داریم به طور خاص با زبانی ساده، به محاسبه میدان الکتریکی حاصل از توزیع‌های مختلفی از بارهای الکتریکی بپردازیم. با ما در ادامه این مقاله همراه باشید.

قبل از پرداختن به محاسبه میدان الکتریکی ناشی از توزیع‌های مختلف بار الکتریکی، نیاز است تا با تعاریفی مقدماتی آشنا شوید.

نیروی الکتریکی

نیروی الکتریکی که غالباً با نام قانون کولن (Coulomb's law) از آن یاد می‌کنند، نیرویی است که دو بار الکتریکی به یکدیگر وارد می‌کنند. این نیرو بسته به نوع بار ذرات، می‌تواند بر دو نوع ربایشی و دافعه باشد. در واقع اگر بار دو ذره هم‌نام باشد (هر دو مثبت یا هر دو منفی) نیرو از جنس دافعه و اگر ناهم‌نام باشد از نوع جاذبه (ربایشی) است. مطابق با قانون کولن، این نیرو با مقدار بار ذرات نسبت مستقیم و با مربع فاصله آن‌ها، نسبت عکس دارد.

$$\large F = \frac{1}{4\pi \epsilon_{0}} \frac{q_{1}q_{2}}{r^{2}}$$
(1)

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

در رابطه فوق $$q_{1}$$ و $$q_{2}$$ مقدار بار ذرات است که به صورت $$q=ne$$ محاسبه می‌شود. $$e$$ نیز مقدار بار الکتریکی (بار الکترون و بار پروتون) است که به صورت یک ثابت جهانی $$1.60217662 \times 10^{-19}\ (C)$$ در نظر گرفته می‌شود. $$n$$ نیز عددی صحیح است که تعداد بار را مشخص می‌کند. به عبارت دیگر، علامت‌های مثبت $$n$$ برای بار الکتریکی مثبت و علامت‌های منفی $$n$$ برای بار الکتریکی منفی استفاده می‌شوند. اگر با توزیع‌های مختلفی از بار الکتریکی مواجه بودیم، قانون کولن قابل تعمیم بوده و شکل انتگرالی به خود می‌گیرد.

توزیع‌های مختلف بار الکتریکی

جهت محاسبه مقدار بار الکتریکی ساختارهای مختلفی از اجسام (خطی، سطحی و حجمی)، نیاز به تعریف پارامتر‌های جدیدی داریم که مقدار بار الکتریکی را به ساختار جسم (خطی، سطحی و حجمی) مرتبط سازد. به عبارت دیگر، پارامتر مذکور از جنس چگالی بوده که به شکل زیر برای ۳ حالت خطی، سطحی و حجمی تعریف می‌شود.

$$\large \lambda = \frac{q}{l}\ (\frac{C}{m})$$
(2)

$$\large \sigma = \frac{q}{A}\ (\frac{C}{m^{2}})$$
(3)

$$\large \rho = \frac{q}{V}\ (\frac{C}{m^{3}})$$
(4)

برخی مراجع نماد طول را با $$s$$ نشان می‌دهند. دقت داشته باشید تا این نماد را با نماد مساحت که غالباً با $$S$$ نمایش داده می‌شود اشتباه نگیرید.

میدان الکتریکی

در مبحث قانون کولن دیدیم که دو ذره باردار به یکدیگر نیرو وارد می‌کنند. سوالی که ممکن است مطرح شود، این است که این دو ذره باردار چگونه به یکدیگر نیرو وارد می‌کنند؟ یا یک بار الکتریکی چگونه حضور بار دیگری را در نزدیکی خود احساس می‌کند؟

پاسخ این سوال در خاصیتی است که یک بار الکتریکی در فضای پیرامون خود ایجاد می‌کند. چنین خاصیت‌هایی در فیزیک با نام میدان بیان می‌شوند. در اینجا یک بار الکتریکی (مثلاً $$q_{1}$$) در فضای اطراف خود میدان الکتریکی ایجاد می‌کند. حال اگر ذره باردار دیگری ($$q_{2}$$) در نزدیکی بار مذکور قرار گیرد، یعنی داخل میدان الکتریکی ناشی از آن (بار $$q_{1}$$) قرار گیرد، از طرف میدان الکتریکی، به آن نیرو وارد می‌شود. این نیرو، همان نیرویی است که از قانون کولن محاسبه می‌شود.

$$\large \overrightarrow{E} = \frac{\overrightarrow{F}}{q_{2}}\ (\frac{N}{C}) \ \Rightarrow \ E = \frac{1}{4\pi\epsilon_{0}}\frac{q_{1}}{r^{2}}$$
(5)

در رابطه فوق، $$r$$ فاصله بار تا نقطه‌ای است که در آن میدان الکتریکی محاسبه می‌شود. از آنجایی که نیرو کمیتی برداری است، میدان الکتریکی نیز کمیتی برداری با واحد سنجش $$\frac{N}{C}$$ است. البته در علوم مهندسی بر اساس رابطه‌ میدان الکتریکی و ولتاژ، واحد سنجش ($$\frac{V}{m}$$) برای میدان الکتریکی مرسوم‌تر است.

$$\large V_{f}-V{i}=\int_{i}^{f}E.dx$$
(6)

به صورت کیفی، مقدار میدان الکتریکی را با خطوطی همانند شکل‌ زیر نشان می‌دهند. مطابق با رابطه (۵)، هرچه به بار الکتریکی نزدیک‌تر شویم مقدار میدان الکتریکی افزایش یافته و به صورت کیفی تعداد یا چگالی خطوط بیشتر می‌شود.

مفهوم میدان

بیان دقیق مفهوم میدان خارج از سطح این مقاله است. اما بد نیست تا اطلاعاتی کلی در این خصوص داشته باشید. در فیزیک و علوم مهندسی مرتبط، منظور از میدان، کمیت‌هایی فیزیکی هستند که آن‌ها را به هر یک از نقاط مکان (به طور دقیق‌تر فضا - زمان) نسبت می‌دهیم. یک میدان می‌تواند اسکالر، بردار، اسپینور یا در حالت عمومی‌تر یک تانسور باشد.

به عنوان مثال تابع چگالی (جرم، بار الکتریکی و ...) یک میدان اسکالر و میدان گرانشی، میدان الکتریکی و میدان مغناطیسی یک میدان برداری به حساب می‌آیند. جهت مشخص کردن میدان‌های برداری در هر نقطه از فضا، به یک عدد جهت بیان اندازه (مقدار) و سه عدد برای بیان جهت در فضا ۳ بعدی نیاز است. میدان‌ها نیز می‌توانند بر دو نوع کلاسیک یا کوانتومی باشند. که میدان‌های کلاسیک با اعداد و میدان‌های کوانتومی با عملگرهای کوانتومی مشخص می‌شوند.

میدان‌ها می‌توانند حالتی را در فضا ایجاد کنند که قابل آشکارسازی است. به طور مثال اگر یک ذره باردار را در آن فضایی قرار دهیم که در آن میدان الکتریکی وجود داشته باشد، از سمت میدان موجود در آن فضا، به آن نیرو وارد می‌شود. در فیزیک مدرن و کوانتومی بیان می‌شود که میدان‌ها دارای تکانه نیز هستند که این مسئله مفهوم میدان‌ را حقیقی‌تر یا ملموس‌تر می‌کند.

محاسبه میدان الکتریکی

در بخش قبل دیدیم که میدان الکتریکی حاصل از یک ذره باردار به شکل زیر است.

$$\large E = \frac{1}{4\pi\epsilon_{0}}\frac{q}{r^{2}}$$
(7)

مطابق با اصل برهمنهی میدان‌های الکتریکی، میدان الکتریکی ناشی از چندین بار الکتریکی در فضا برابر است با مجموع میدان‌هایی که هر یک از بارهای الکتریکی در غیاب سایر بارها در فضا ایجاد می‌کنند، یعنی:

$$\large \overrightarrow{E_{T}} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}} + ...$$
(8)

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

حال اگر تعداد بارها آنقدر زیاد باشد که بتوان توزیع پیوسته‌ای از ذرات باردار را در فضا در نظر گرفت، می‌توانیم رابطه فوق را به صورت انتگرالی به کار ببریم. در واقع محاسبه میدان الکتریکی برآیند حاصل از مجموعه‌ای از ذرات باردار به صورت زیر است:

$$\large \overrightarrow{E_{T}} = \int dE$$
(9)

با جایگذاری $$E$$ از رابطه (7) داریم:

$$\large \overrightarrow{E_{T}} = \int dE = \int \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^{2}}$$
(10)

در اینجا تعیین جز دیفرانسیلی $$dq$$ اهمیت بسیار زیادی دارد. متناسب با ساختار جسم (خطی، سطحی و حجمی) مقدار $$dq$$ می‌تواند به ۳ شکل زیر در آید.

$$\large dq = \lambda dl$$
(11)

$$\large dq = \sigma dA$$
(12)

$$\large dq = \rho dV$$
(13)

در ادامه این مطلب، در قالب مثال‌هایی آموزشی، نحوه محاسبه میدان الکتریکی با استفاده از روابط فوق را آموزش می‌دهیم.

محاسبه میدان الکتریکی ناشی از میله یک طرف نامحدود

در این قسمت می‌خواهیم به محاسبه میدان الکتریکی ناشی از یک میله یک طرف نامحدود با چگالی بار خطی λ، در نقطه P مطابق با شکل زیر بپردازیم. نقطه P به اندازه R از میله فاصله دارد.

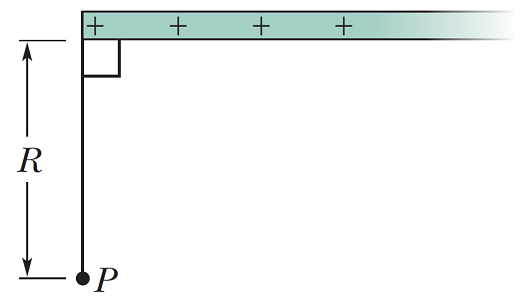
جهت استفاده از رابطه $$\overrightarrow{E_{T}} = \int dE = \int \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^{2}}$$، بدیهی است که ابتدا باید جزء دیفرانسیلی بار $$dq$$ را مشخص کرد. از آنجایی که توزیع چگالی بار به صورت خطی است، $$dq$$ را می‌توانیم به صورت $$dq = \lambda dl$$ در رابطه جایگذاری کنیم. هر جزء دیفرانسیلی بار $$dq$$ میدان $$dE$$ را ایجاد می‌کند که هدف ما به دست آوردن برآیند (مجموع) تمامی $$dE$$‌های ایجاد شده است. بر اساس فیزیک شکل (۳)، هر $$dE$$ ایجاد شده قابل تجزیه در دو راستای $$x$$ و $$y$$ است (همانند شکل ۵).

مطابق با شکل فوق، به علت عدم وجود تقارن، هیچ کدام از مولفه‌های میدان یکدیگر را خنثی نکرده و باید هر کدام را به صورت جداگانه حساب کنیم. اگر میله از دو طرف نامحدود بود، آنگاه مولفه‌های $$dE_{x}$$ یکدیگر را خنثی می‌کردند. با توجه به شکل داریم:

$$\large E_{x} = - \int dE\sin\alpha$$
(14)

$$\large E_{y} = \int dE\cos\alpha$$
(15)

علامت منفی برای $$E_{x}$$ به این علت است که در قسمت منفی محور $$x$$ قرار دارد. با رسم خط فرضی میدان از یک جزء دیفرانسیلی بار $$dq$$، در واقع یک مثلث تشکیل شده که از زاویه راس آن (α) برای تجزیه میدان به مولفه‌های $$E_{x}$$ و $$E_{y}$$ استفاده می‌کنیم. با توجه به مطلب گفته شده داریم:

$$\large \sin \alpha = \frac{x}{(x^{2}+R^{2})^{\frac{1}{2}}}$$
(16)

$$\large \cos \alpha = \frac{R}{(x^{2}+R^{2})^{\frac{1}{2}}}$$
(17)

با جایگذاری دو رابطه فوق در دو رابطه (14) و (15) و استفاده از رابطه (10) نتیجه می‌شود (در اینجا $$dl$$ همان جز $$dx$$ است):

$$\large E_{x} = - \int_{0}^{\infty} dE\sin\alpha = - \int_{0}^{\infty} \frac{1}{4\pi\epsilon_{0}}\frac{\lambda dx}{(x^{2}+R^{2})}\frac{x}{(x^{2}+R^{2})^{\frac{1}{2}}}$$

$$\Rightarrow \large E_{x} = - \int_{0}^{\infty} dE\sin\alpha = \int_{0}^{\infty} \frac{1}{4\pi\epsilon_{0}}\frac{-\lambda xdx}{(x^{2}+R^{2})^{\frac{3}{2}}}$$
(18)

به طور مشابه برای $$E_{y}$$ نیز داریم:

$$\large E_{y} = \int_{0}^{\infty} dE\sin\alpha = \int_{0}^{\infty} \frac{1}{4\pi\epsilon_{0}}\frac{\lambda Rdx}{(x^{2}+R^{2})^{\frac{3}{2}}}$$
(19)

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

دو انتگرال رابطه (18) و (19) با تغییر متغیر $$x = R \tan \alpha$$ قابل حل هستند. همچنین با استفاده از دو رابطه انتگرالی زیر، دو رابطه فوق سریع‌تر حل می‌شوند:

$$\large \int \frac{dx}{(x^{2}+a^{2})^{\frac{3}{2}}} = \frac{x}{a^{2}\sqrt{x^{2}+a^{2}}}$$
(20)

$$\large \int \frac{xdx}{(x^{2}+a^{2})^{\frac{3}{2}}} = \frac{-1}{\sqrt{x^{2}+a^{2}}}$$
(21)

در نتیجه میدان نهایی (کل) به صورت زیر محاسبه می‌شود.

$$\large E = \frac{\lambda}{4 \pi \epsilon_{0}}(- \widehat{x} + \widehat{y})$$
(22)

از رابطه فوق مشخص است که میدان کل $$E$$ با امتداد محور $$y$$ زاویه ۴۵ درجه می‌سازد.

محاسبه میدان الکتریکی ناشی از حلقه باردار

در این قسمت در نظر داریم تا میدان الکتریکی ناشی از یک حلقه باردار را روی محور حلقه مطابق با شکل زیر محاسبه کنیم. به عبارت دیگر، قصد در محاسبه میدان الکتریکی برآیند، ناشی از جز‌ءهای دیفرانسیلی $$ds$$ (دیفرانسیل طول) در حلقه‌ای به شعاع $$R$$ داریم.

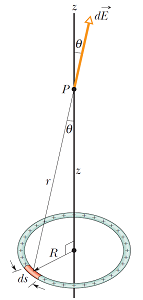
در این مثال، از آنجایی که ساختار حلقه‌ را می‌توانیم طولی در نظر بگیریم، چگالی بار الکتریکی آن خطی است. در نتیجه با استفاده از دو رابطه (10) و (11) داریم:

$$\large dE = \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^{2}} = \frac{1}{4\pi\epsilon_{0}}\frac{\lambda ds}{r^{2}}$$
(23)

همان‌طور که پیش‌تر اشاره کردیم، $$r$$ فاصله بار (در اینجا جز دیفرانسیلی $$dq$$) تا نقطه‌ای است که قصد محاسبه میدان الکتریکی در آن نقطه را داریم. مطابق با شکل (۴) این فاصله از رابطه فیثاغورث به راحتی به دست می‌آید. در نتیجه داریم:

$$\large dE = \frac{1}{4\pi\epsilon_{0}}\frac{\lambda ds}{r^{2}} = \frac{1}{4\pi\epsilon_{0}}\frac{\lambda ds}{(R^{2}+z^2)}$$
(24)

همان‌طور که در شکل (4) مشاهده کردید، بردار میدان الکتریکی با راستای محور حلقه زاویه‌ دارد. در نتیجه جهت محاسبه میدان الکتریکی برآیند باید بردار میدان الکتریکی را تجزیه کنیم. جهت مرور بردار‌ها، به مقاله «بردار — به زبان ساده» مراجعه کنید. با استفاده از روابط مثلثاتی در مثلت قائم‌الزاویه داریم:

$$\large \cos\theta = \frac{z}{r} = \frac{z}{(R^{2}+z^{2})^{\frac{1}{2}}}$$
(25)

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

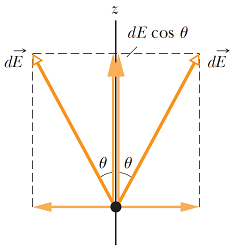
در اینجا تنها مولفه‌های $$dE\cos\theta$$ در یک راستا هستند که باید مجموع (انتگرال) آن‌ها را محاسبه کنیم. مطابق با شکل فوق، مجموع مولفه‌های $$dE\sin\theta$$ یکدیگر را خنثی می‌کنند. با استفاده از رابطه (25) نتیجه می‌شود:

$$\large dE\cos\theta = \frac{1}{4\pi\epsilon_{0}}\frac{\lambda ds}{r^{2}}\cos\theta = \frac{1}{4\pi\epsilon_{0}}\frac{z\lambda ds}{(R^{2}+z^2)^{\frac{3}{2}}}$$
(26)

بدیهی است که جهت محاسبه میدان الکتریکی برآیند، باید از رابطه فوق انتگرال بگیریم. پارامتر‌هایی که در جزء دیفرانسیلی $$ds$$ در رابطه فوق ضرب شده‌اند، هیچ وابستگی به $$ds$$ نداشته و به راحتی از انتگرال بیرون می‌آیند. حدود انتگرال نیز باید کل حلقه را پوشش دهد. در واقع مجموع جزءهای دیفرانسیلی $$ds$$ همان محیط حلقه ($$2\pi R$$) است. در نتیجه:

$$\large E = \int dE\cos\theta = \int\frac{1}{4\pi\epsilon_{0}}\frac{z\lambda ds}{(R^{2}+z^2)^{\frac{3}{2}}} = \frac{1}{4\pi\epsilon_{0}}\frac{z\lambda}{(R^{2}+z^2)^{\frac{3}{2}}}\int_{0}^{2\pi R}ds$$
(27)

$$\large \Rightarrow E = \frac{1}{4\pi\epsilon_{0}}\frac{z\lambda 2\pi R}{(R^{2}+z^2)^{\frac{3}{2}}} \ \Rightarrow \ E = \frac{1}{4\pi\epsilon_{0}}\frac{qz}{(R^{2}+z^2)^{\frac{3}{2}}}$$
(28)

در عبارت فوق، حاصل ضرب چگالی بار خطی λ در محیط حلقه ($$2\pi R$$) مقدار بار کل $$q$$ است.

محاسبه میدان الکتریکی ناشی از صفحه دیسک

در این بخش به محاسبه میدان الکتریکی (روی محور) ناشی از یک دیسک باردار با چگالی بار صفحه‌ای σ می‌پردازیم.

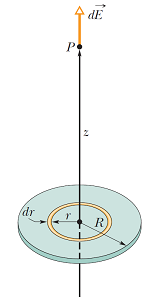
مطابق با شکل فوق، جز دیفرانسیلی $$dq$$ را به صورت زیر تعریف می‌کنیم. ($$A=\pi R^{2}$$: مساحت دیسک (دایره))

$$\large dq = \sigma dA=\sigma(2\pi rdr)$$
(29)

یک راه آسان جهت ادامه محاسبات استفاده از میدان الکتریکی حلقه باردار است که در بخش قبل آن را محاسبه کردیم. به عبارت دیگر تعداد بسیار زیادی حلقه که کنار یکدیگر قرار گرفته‌اند (با افزایش شعاع) یک دیسک را می‌سازند. پس با محاسبه میدان الکتریکی برآیند این حلقه‌ها می‌توان میدان الکتریکی دیسک را روی محور آن محاسبه کرد. نکته‌ مهمی که در اینجا باید به آن توجه کرد در نظر گرفتن $$dq$$ به صورت چگالی بار صفحه‌ای است. با استفاده از رابطه (10) و (12) داریم (در اینجا $$r$$ شعاع حلقه است - شکل 6):

$$\large \int dE = \frac{1}{4\pi\epsilon_{0}}\frac{zdq}{(r^{2}+z^2)^{\frac{3}{2}}}$$
(30)

$$\large \Rightarrow \int dE = \frac{1}{4\pi\epsilon_{0}}\frac{z\sigma dA}{(r^{2}+z^2)^{\frac{3}{2}}}$$
(31)

$$\large \Rightarrow E = \int dE = \frac{\sigma z}{4\epsilon_{0}}\int (r^{2}+z^2)^{-\frac{3}{2}}2rdr$$
(32)

روش‌های مختلفی جهت حل انتگرال فوق وجود دارد. یکی از راه‌های ساده استفاده از رابطه ریاضی زیر است:

$$\large \int X^{m}dX = \frac{X^{m+1}}{m+1}$$
(33)

با در نظر گرفتن $$X=\left(r^{2}+z^{2}\right)$$ و $$m=-\frac{3}{2}$$ داریم:

$$\large E = \frac{\sigma z}{4 \varepsilon_{0}}\left[\frac{\left(z^{2}+r^{2}\right)^{-\frac{1}{2}}}{-\frac{1}{2}}\right]_{0}^{R}$$
(34)

$$\large \Rightarrow E = \frac{\sigma}{2 \varepsilon_{0}}\left(1-\frac{z}{\sqrt{z^{2}+R^{2}}}\right)$$
(35)

یکی از نتایج مهمی که از رابطه فوق می‌توان به آن رسید، میدان الکتریکی صفحه بی‌نهایت بزرگ است. در واقع با میل کردن $$R$$ به سمت بی‌نهایت، ساختار مذکور را می‌توانیم یک صفحه بی‌نهایت در نظر بگیریم. با محاسبه حد رابطه (35) با شرط $$R\rightarrow\infty$$، میدان الکتریکی ناشی از یک صفحه باردار بی‌نهایت بزرگ برابر با مقدار زیر می‌شود:

$$\large E = \frac{\sigma}{2 \varepsilon_{0}}$$
(36)

محاسبه میدان الکتریکی دو قطبی

در این بخش قصد داریم به محاسبه میدان الکتریکی حاصل از یک دوقطبی (یک بار مثبت و یک بار منفی) در نقطه‌ای در راستای محور دو قطبی، مطابق با شکل زیر بپردازیم.

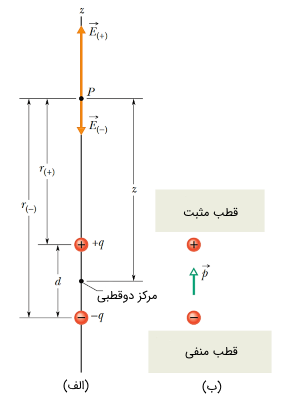
مطابق با شکل (۷) فاصله بین قطب (بار) مثبت و قطب (بار) منفی به اندازه $$d$$ و فاصله نقطه‌ای که در آن قصد محاسبه میدان الکتریکی را داریم، تا مرکز دوقطبی $$z$$ است. میدان الکتریکی در نقطه $$P$$ عبارت است از:

$$\large E_{P}=E_{+}-E_{-}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r_+^2}-\frac{1}{4\pi\epsilon_{0}}\frac{q}{r_-^2}$$
(37)

طبق شکل (۷)، فواصل $$r_{+}$$ و $$r_{-}$$ را می‌توانیم به صورت زیر تعریف کنیم.

$$\large r_{+}=z-\frac{d}{2}$$
(38)

$$\large r_{-}=z+\frac{d}{2}$$
(39)

با جایگذاری در معادله (37) و فاکتورگیری از $$z^{2}$$ نتیجه می‌شود:

$$\large E_{P}=\frac{q}{4\pi\epsilon_{0}z^{2}}(\frac{1}{(1-\frac{d}{2z})^{2}}-\frac{1}{(1+\frac{d}{2z})^{2}})$$
(40)

با استفاده از اتحاد $$(a+b)(a-b)=a^{2}-b^{2}$$ قسمت پرانتزی رابطه فوق را می‌توانیم به شکل زیر بنویسیم:

$$\large E_{P}=\frac{q}{4\pi\epsilon_{0}z^{2}}\frac{\frac{2d}{z}}{(1-(\frac{d}{2z})^{2})^{2}}$$
(41)

از آنجایی که معمولاً میدان الکتریکی را در نقطه‌ای دور از دوقطبی به دست می‌آوریم ($$z>>d$$)، حاصل $$\frac{d}{2z}<<1$$ شده و لذا از آن صرف‌نظر می‌کنیم. در نتیجه:

$$\large E_{P}=\frac{1}{2\pi\epsilon_{0}}\frac{qd}{z^{3}}$$
(42)

در رابطه فوق به عبارت $$qd$$ بردار قطبش گفته شده که آن را با $$p$$ نمایش می‌دهند. جهت $$p$$ در یک دوقطبی همیشه از بار منفی به سمت بار مثبت است (شکل 7). در شکل (8) خطوط میدان یک دوقطبی الکتریکی نشان داده شده است.

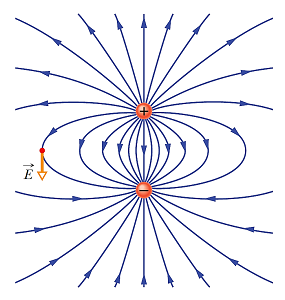
محاسبه میدان الکتریکی با استفاده از قانون گاوس

در مقاله «قانون گاوس (Gauss Law) و شار الکتریکی — یادگیری با مثال» با مفاهیم قانون گاوس و استفاده از آن به طور کامل آشنا شدید. همان‌طور که در بخش‌های قبل ملاحظه کردید، استفاده از رابطه $$\overrightarrow{E_{T}} = \int dE = \int \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^{2}}$$ ، جهت محاسبه میدان الکتریکی روشی با محاسبات نسبتاً طولانی است.

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

به عبارت دیگر روش مذکور یک روش کلی جهت محاسبه میدان الکتریکی برآیند ناشی از تمامی جزء‌های دیفرانسیلی $$dq$$ است. استفاده از این روش برای ساختارهای پیچیده نیازمند کامپیوتر است.

اما روشی ساده‌تر جهت محاسبه میدان الکتریکی برای ساختارهایی که دارای تقارن هستند نیز وجود دارد. این روش که به قانون گاوس موسوم است، معادله‌ای به شکل زیر دارد:

$$\large \begin{equation} \Phi = \oint \vec{E} \cdot d \vec{S} \end{equation} = \frac{q_{enc}}{\varepsilon_{0}}$$
(43)

در رابطه فوق، $$\oint$$ به معنی انتگرال سطح بسته است. این سطح بسته به سطح گاوسی نیز معروف بوده و بیانگر سطحی است که بار خالص $$q_{enc}$$ را شامل می‌شود. همچنین مساحت سطح گاوسی مذکور برابر با $$S$$ است. در واقع قانون گاوس بیان می‌کند که شار الکتریکی ($$\Phi$$) گذرنده از سطح بسته‌ای که بار $$q_{enc}$$ شامل می‌شود برابر با مقدار $$\frac{q_{enc}}{\varepsilon_{0}}$$ است. در اکثر مسائل، ساختارهای مورد بررسی دارای تقارن بوده و حاصل ضرب نقطه‌ای $$\vec{E} \cdot d \vec{S}$$ به شکل ساده‌تر $$ES$$ در می‌آید. در واقع زاویه بین بردار میدان الکتریکی و جزء دیفرانسیلی سطح، صفر درجه است (شکل 9). همچنین غالباً $$E$$ وابستگی به جزء دیفرانسیلی $$dS$$ نداشته و به راحتی از انتگرال بیرون می‌آید.

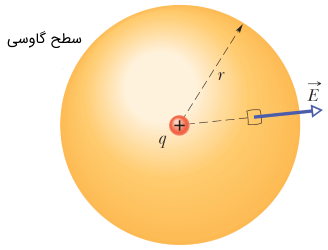
حاصل انتگرال $$dS$$ که معنی جمع تمامی جزء‌های دیفرانسیلی سطح است، برابر با مساحت سطح گاوسی در نظر گرفته شده است. جهت آشنایی بیشتر با چگونگی استفاده از قانون گاوس برای محاسبه میدان الکتریکی یک توزیع بار متقارن به مثال‌های زیر توجه کنید.

محاسبه میدان الکتریکی ناشی از خط پیوسته بار بی‌نهایت با استفاده از قانون گاوس

در اینجا قصد داریم تا با استفاده از قانون گاوس به محاسبه میدان الکتریکی توزیع بار مذکور بپردازیم. مطابق با شکل زیر، بهترین و متناسب‌ترین سطح گاوسی که می‌توان در نظر گرفت، سطحی استوانه‌ای شکل است.

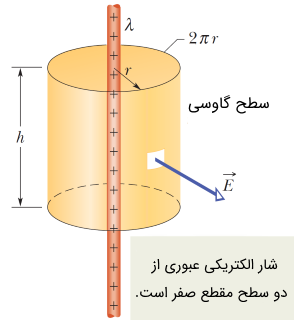
مطابق با شکل فوق، از آنجایی که زاویه بین خطوط میدان الکتریکی (شار الکتریکی) و جز‌ءهای دیفرانسیلی $$dS$$ صفر درجه است، میدان الکتریکی $$E$$ به راحتی از انتگرال بیرون می‌آید. در نتیجه:

$$\large \oint E.dS=\frac{q_{in}}{\varepsilon_{0}} \Rightarrow \ E\oint dA = \frac{q_{in}}{\varepsilon_{0}} \Rightarrow E = \frac{q_{in}}{\varepsilon_{0}2\pi rh}$$
(44)

پیش‌تر اشاره کردیم که $$q_{in}$$ مقدار بار خالص احاطه شده توسط سطح گاوسی است. از آنجایی که توزیع بار خطی است، مقدار $$q_{in}$$ را می‌توان بر حسب چگالی بار به صورت $$q_{in} = \lambda l$$ نوشت. در اینجا پارامتر $$l$$ که بیانگر طول توزیع بار خطی است، برابر با ارتفاع استوانه (سطح گاوسی) است ($$l=h$$). در نتیجه حاصل عبارت فوق به شکل زیر در می‌آید:

$$\large E = \frac{\lambda}{2 \pi \varepsilon_{0} r}$$
(45)

همان‌طور که مشاهده کردید با استفاده از قانون گاوس، محاسبه میدان الکتریکی ساختارهای متقارن بسیار راحت بوده و محاسبات ساده و کوتاهی دارد.

محاسبه میدان الکتریکی ناشی از کره باردار با استفاده از قانون گاوس

جهت محاسبه میدان الکتریکی ساختارهای کروی، به دلیل وجود تقارن به راحتی می‌توان از قانون گاوس استفاده کرد. برای یک توزیع بار کروی، بهترین سطح گاوسی که می‌توان در نظر گرفت، سطحی کروی (مساحت کره : $$4\pi r^{2}$$) است. جهت محاسبه میدان الکتریکی خارج از توزیع کروی بار با شعاع $$R$$، سطح گاوسی کروی با شعاع $$r>R$$ را در نظر می‌گیریم.

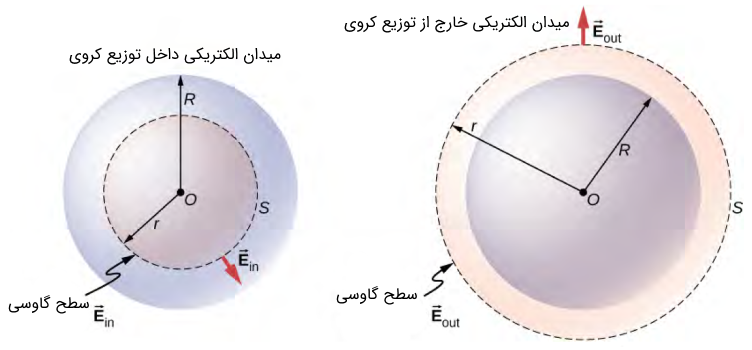
در اینجا نیز به دلیل تقارن و عدم وابستگی میدان الکتریکی $$E$$ به جزء دیفرانسیلی $$dS$$، محاسبات ساده و کوتاه خواهند بود. مطابق با قانون گاوس داریم:

$$\large \begin{equation} \oint \vec{E} \cdot d \vec{S} \end{equation} = \frac{q_{enc}}{\varepsilon_{0}} \Rightarrow ES = \frac{q_{enc}}{\varepsilon_{0}}$$

$$\large \Rightarrow E = \frac{q_{enc}}{\varepsilon_{0}S} = \frac{q}{4 \pi \varepsilon_{0} r^{2}}$$
(46)

همان‌طور که مشاهده می‌کنید، میدان الکتریکی یک توزیع بار کروی، برابر با میدان الکتریکی یک بار نقطه‌ای است که از قانون کولن به دست آمد. در واقع در اکثر مسائل و کاربرد‌های الکترومغناطیسی، بار الکتریکی توزیع‌های کروی را، به صورت متمرکز در مرکز آن فرض می‌کنند.

جهت محاسبه میدان الکتریکی درون توزیع کروی بار نیز به راحتی می‌توان از قانون گاوس استفاده نمود. مطابق با شکل (۱۱)، سطحی کروی با شعاع $$r$$ را درون توزیع کروی بار در نظر می‌گیرم. نکته‌ای که در اینجا باید به آن دقت کرد، مقدار بار محصور شده در سطح گاوسی است. مطابق با شکل واضح است که مقدار بار محصور شده توسط سطح گاوسی، کمتر از بار کل $$q$$ است. از آنجایی که توزیع بار متقارن و یکنواخت است، مقدار چگالی بار حجمی محصور شده را می‌توان کسری از چگالی بار کل در نظر گرفت. یعنی:

$$\large q = \rho V \Rightarrow \rho_{1} = \rho_{2} \rightarrow \frac{q_{enc}}{\frac{4}{3} \pi r^{3}} = \frac{q}{\frac{4}{3} \pi R^{3}}$$

$$\large \Rightarrow q_{enc} = q \frac{r^{3}}{R^{3}}$$
(47)

با قرار دادن $$q_{enc}$$ در معادله قانون گاوس داریم:

$$\large \begin{equation} \oint \vec{E} \cdot d \vec{S} \end{equation} = \frac{q_{enc}}{\varepsilon_{0}} \Rightarrow ES = \frac{q_{enc}}{\varepsilon_{0}}$$

$$\large \Rightarrow E = \frac{q_{enc}}{\varepsilon_{0}S} = \frac{q \frac{r^{3}}{R^{3}}}{4 \pi \varepsilon_{0} r^{2}}$$

$$\Rightarrow \begin{equation} E = \left(\frac{q}{4 \pi \varepsilon_{0} R^{3}}\right) r \end{equation}$$
(48)

مطابق با محاسبات فوق، می‌توان تغییرات میدان الکتریکی حاصل از یک توزیع کروی بار را بر حسب تغییرات مسافت (شعاع) به صورت زیر رسم کرد:

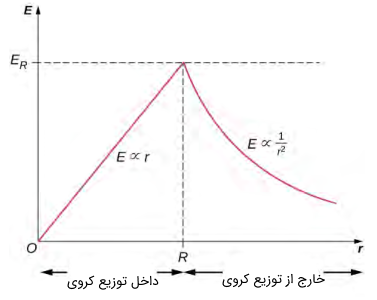
همان‌طور که مشاهده می‌کنید، مقدار میدان الکتریکی در نقطه‌ای روی سطح توزیع بار بیشینه است.

محاسبه میدان الکتریکی صفحه (ورق) باردار بی‌نهایت

با استفاده از قانون گاوس به راحتی می‌توان میدان الکتریکی را در نزدیکی یک صفحه باردار به دست آورد. شکل زیر را در نظر بگیرید.

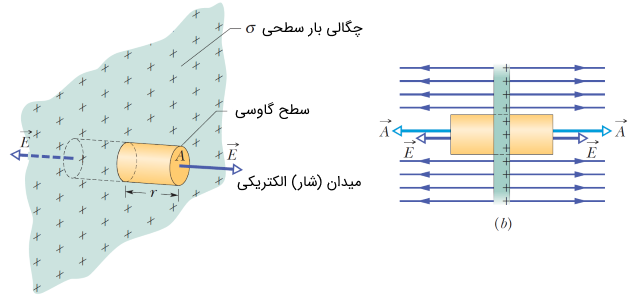
در شکل فوق یک سطح گاوسی استوانه‌ای در نظر گرفته شده است. البته الزامی به در نظر گرفتن سطح استوانه‌ای نیست. به طور مثال سطحی مستطیل شکل را نیز می‌توانید در نظر بگیرید. نکته‌ای که در اینجا باید به آن توجه کرد در مفهوم قانون گاوس، یعنی شار الکتریکی گذرنده از سطح گاوسی است. با توجه به شکل فوق، متناسب با سطح گاوسی، تنها شار گذرنده از دو سطح مقطع غیر صفر است (شکل 13 - b). پس مطابق با قانون گاوس داریم:

$$\large \begin{equation} \Phi = \oint \vec{E} \cdot d \vec{S} \end{equation} = \frac{q_{enc}}{\varepsilon_{0}} \Rightarrow \varepsilon{0}(ES+EA) = \sigma S \Rightarrow E = \frac{\sigma}{2\varepsilon_{0}}$$
(49)

محاسبه میدان الکتریکی بین دو صفحه رسانا باردار موازی (خازن)

مطابق با مطلب بخش قبل و شکل زیر، محاسبه میدان الکتریکی بین دو صفحه باردار با استفاده از قانون گاوس به راحتی امکان‌پذیر است. می‌دانیم که میدان الکتریکی در دو شکل (۱۴ - a) و (۱۵ - b) مطابق با مطالب قسمت قبل به صورت $$E = \frac{\sigma_{1}}{2\varepsilon_{0}}$$ است. حال اگر این دو صفحه را در نزدیکی یکدیگر قرار دهیم، با توجه به اینکه بارهای اضافی روی سطح رسانا قرار می‌گیرند و همچنین، به دلیل ناهم‌نام بودن بارهای دو صفحه، مطابق با شکل (۱۴ - پایین) دو صفحه تمایل به جذب یکدیگر دارند.

در واقع با نزدیک کردن دو صفحه به یکدیگر، تمامی بارها به سمت یک لبه از صفحه می‌آیند. اگر توزیع چگالی بار را یکنواخت فرض کنیم، می‌توانیم بگوییم که مقدار بار روی وجه داخلی صفحات دو برابر شده است. پس چگالی بار سطحی جدید روی هر وجه $$2\sigma_{1}$$ است. در نتیجه میدان الکتریکی بین دو صفحه مذکور به صورت زیر محاسبه می‌شود.

$$\large \begin{equation} \Phi = \oint \vec{E} \cdot d \vec{S} \end{equation} = \frac{q_{enc}}{\varepsilon_{0}} \Rightarrow \varepsilon{0}(ES) = 2\sigma_{1} S \Rightarrow E = \frac{2\sigma_{1}}{\varepsilon_{0}} = \frac{\sigma}{\varepsilon_{0}}$$
(50)

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

در عبارت فوق، $$2\sigma_{1}$$ را برابر با چگالی بار سطحی جدید $$\sigma$$ در نظر گرفتیم ($$2\sigma_{1} = \sigma$$).

توجه داشته باشید که رابطه فوق را می‌توان میدان الکتریکی بین دو صفحه خازن در نظر گرفت. با توجه به رابطه میدان و ولتاژ  ($$V = Ed$$) و رابطه ظرفیت خازن ($$C = \frac{q}{V}$$) داریم:

$$\large C = \frac{q}{Ed} = \frac{q}{\frac{\sigma}{\varepsilon_{0}}d} = \varepsilon_{0} \frac{A}{d}$$
(51)

یکی دیگر از کاربرد‌های مهم قانون گاوس، استفاده از آن جهت محاسبه ظرفیت خازن‌ است که در مقاله «ظرفیت خازن — یادگیری با مثال» به تفضیل در مورد آن بحث کردیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۲
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش الکترومغناطیس ۱
• امواج رادیویی -- به زبان ساده
• امپدانس و محاسبه آن -- به زبان ساده
• خازن در جریان متناوب -- به زبان ساده

^^