محاسبه انتگرال در پایتون — راهنمای گام به گام

اغلب در حسابان به انتگرال‌هایی بر می‌خوریم که ممکن است از طریق تحلیلی نتوان پاسخی برای آن‌ها یافت. حتی احتمال دارد برای محاسبه انتگرال به روش تحلیلی زمان طولانی لازم باشد. در این میان می‌توان از روش‌های عددی و به کمک زبان‌های برنامه‌نویسی، محاسبات را انجام داده و به پاسخ نسبتا دقیقی برسیم. در این نوشتار محاسبه انتگرال به شیوه عددی را مرور کرده و ده گام برای محاسبه انتگرال در پایتون را معرفی می‌کنیم.

به منظور آشنایی با انتگرال و نحوه محاسبه آن بهتر است مطلب انتگرال و روش های محاسبه — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال‌ به روش عددی نیز خالی از لطف نیست.

محاسبه انتگرال در پایتون

در این نوشتار، محاسبه انتگرال در پایتون را به سه بخش و ده گام تقسیم کرده‌ایم. در بخش اول با محاسبه عددی انتگرال و الگوریتم‌ یا روش محاسبه انتگرال بوسیله قسمت‌های مستطیلی آشنا می‌شویم. هر چند در بخش اول احتیاج به مفاهیمی از حسابان داریم ولی سعی می‌کنیم که در مواردی که پیچیدگی در درک مطالب وجود دارد، اصطلاحات و مباحث را به شکل ساده مرور کنیم.

فیلم آموزش محاسبات عددی در پایتون Python در فرادرس

کلیک کنید

برنامه‌نویسی به زبان پایتون برای پیاده‌سازی این الگوریتم را در بخش دوم خواهیم دید. به این ترتیب در هنگام کد نویسی هر جا نیاز باشد، از نحوه عملکرد دستورات نیز اطلاعاتی در اختیار خواننده قرار خواهیم داد. در بخش سوم و انتهایی نیز برنامه ایجاد شده را به منظور محاسبه عددی انتگرال‌های مختلف به کار خواهیم گرفت.

هدف از این کار ایجاد بستری است که بواسطه آن بتوانیم انتگرال توابع دلخواه را با سرعت و دقت مناسب محاسبه کنیم. بنابراین می‌توان از نتیجه این نوشتار به عنوان ابزاری محاسباتی برای دانشجویان و محققین استفاده کرد. گام‌های پیاده‌سازی محاسبه انتگرال در پایتون در زیر فهرست شده‌اند.

1. مفهوم انتگرال و انتگرال معین
2. محاسبه تقریبی انتگرال معین به کمک محاسبات عددی
3. تفکیک بازه و استفاده از مقدار میانی هر فاصله
4. دریافت کامپایلر پایتون و ویرایشگر کد Canopy
5. فراخوانی کتابخانه‌های مورد نیاز در پایتون و تعریف متغیرها
6. نوشتن یک تابع در پایتون به عنوان انتگرال‌ده
7. نمایش نتیجه محاسبه انتگرال
8. اجرای برنامه
9. محاسبه انتگرال تابع سینوس
10. توسعه برنامه

گام اول: مفهوم انتگرال و انتگرال معین

انتگرال یکی از مفاهیم مهم و اصلی در حسابان محسوب می‌شود. از انتگرال در بسیاری از علوم مانند محاسبات مالی، نظریه اعداد، فیزیک، شیمی و ... استفاده می‌شود. اگر به تاریخچه محاسبه انتگرال علاقمند هستید بهتر است مطلب نماد انتگرال — با سرگذشت جالب این علامت ریاضی آشنا شوید را مطالعه کنید. همانطور که در تصویر می‌بینید اگر بخواهیم سطح زیر منحنی $$f(x)$$ در بازه $$[a,b]$$ را بدست آوریم، ناگزیر به محاسبه انتگرال هستیم. بنابراین برنامه‌ای که با پایتون خواهیم نوشت، برای محاسبه سطح زیر منحنی توابعی است که روی بازه مورد نظر پیوستگی داشته باشند.

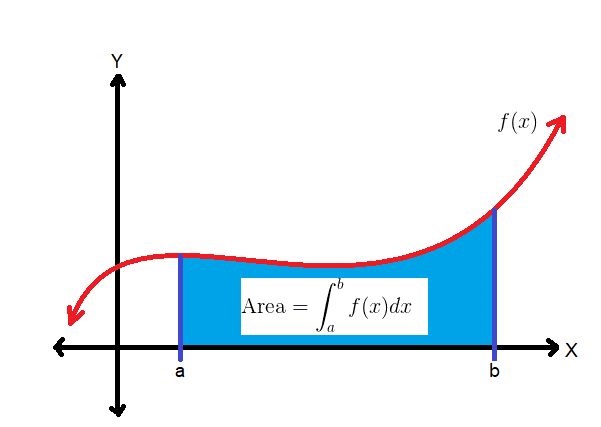
این گونه انتگرال‌ها را «انتگرال معین» (Definite Integral) می‌نامند. در این حالت $$f(x)$$ را انتگرال‌ده و $$dx$$ را دیفرانسیل $$x$$ می‌نامیم. در اینجا Area همان سطح زیر منحنی است.

گام دوم: محاسبه تقریبی انتگرال معین به کمک محاسبات عددی (روش مستطیلی)

رایانه‌ها برای انجام عملیات، احتیاج به دستورالعمل‌هایی دارند که به صورت مرحله‌ به مرحله و یا حلقه‌های تکرار بیان شوند. از این خاصیت برای محاسبه انتگرال معین به صورت عددی استفاده می‌کنیم.

فیلم آموزش ریاضی برای یادگیری ماشین + پیاده سازی در پایتون در فرادرس

کلیک کنید

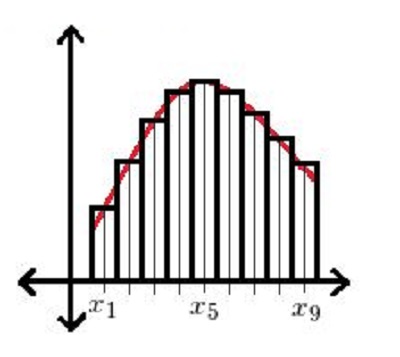
تصور کنید که سطح زیر منحنی تابع $$f(x)$$ به مستطیل‌هایی تقسیم شده باشد. اگر فاصله نقطه $$a$$ تا $$b$$ در بازه مورد نظر را به $$n$$ بخش تقسیم کنیم، عرض هر یک از این مستطیل‌ها بدست می‌آید. از طرفی طول مستطیل‌ها نیز با توجه به مقدار تابع در هر نقطه تعیین می‌شود. به این ترتیب مساحت هر یک از مستطیل‌ها را می‌توان به صورت مقدار عرض مستطیل در طول بدست آورد. هر چه تعداد این مستطیل‌ها بیشتر باشد، دقت محاسبه انتگرال نیز بیشتر خواهد بود. به این منظور لازم است که بازه $$[a,b]$$ به بخش‌های بیشتری تفکیک شود. درست به همین علت است که مقدار انتگرال محاسبه شده را تقریبی در نظر می‌گیرند.

در الگوریتمی که به کار خواهیم برد، بازه $$[a,b]$$ به $$n$$ بخش مساوی تقسیم شده که عرض مستطیل‌ها را می‌سازند و برای طول هر مستطیل نیز مقدار تابع در هر یک از این بخش‌ها در نظر گرفته خواهد شد. از آنجایی که با افزایش تعداد این مستطیل‌ها، میزان محاسبات افزایش می‌یابد، استفاده از یک رایانه و برنامه رایانه‌ای به منظور اجرای چنین کارهای تکراری مناسب است. به علت اینکه برای محاسبه انتگرال، سطح زیر منحنی، به مستطیل‌هایی تفکیک شده، این شیوه را «انتگرال‌گیری به روش مستطیلی» (Rectangular Integral Approximation) می‌نامند. البته روش‌های دیگری نیز در این میان وجود دارد که ممکن است به جای استفاده از مستطیل از مساحت ذوزنقه‌ها کمک گرفته شود. چنین روشی به محاسبه انتگرال به شیوه ذوزنقه‌ای نیز می‌گویند.

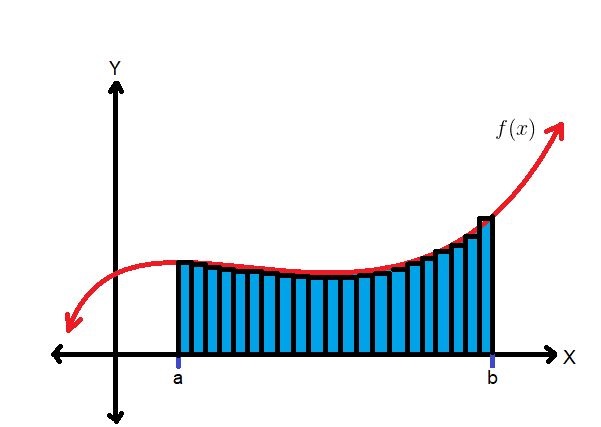
گام سوم: تفکیک بازه و استفاده از مقدار میانی هر فاصله

از آنجایی که باید برای طول هر مستطیل از تابع $$f(x)$$‌ استفاده کنیم، برایمان مهم است که کدام نقطه را به عنوان مقدار تقریبی برای تابع در نظر بگیریم. یک روش برای انجام این کار استفاده از نقطه میانی است. به این ترتیب فاصله $$[a,b]$$ را به صورت زیر افراز می‌کنیم. این بخش همان دیفرانسیل در انتگرال معین را مشخص می‌کند.

$$\large \Delta x=\dfrac{b-a}{n}$$

حال زمان محاسبه طول هر یک از مستطیل‌ها است. برای این کار از نقاط میانی هر یک از بخش‌ها که با $$\overline{x}_i$$ مشخص می‌شود، استفاده می‌کنیم واضح است که محل هر یک از این نقاط را باید به صورت زیر محاسبه کنیم.

$$\large \overline{x}_i=\dfrac{1}{2}(x_{i-1}+x_i)=a+\dfrac{2i-1}{2n}(b-a)$$

به این ترتیب می‌توانیم مطابق رابطه زیر، انتگرال را محاسبه کنیم.

$$\large \int_a^bf(x)dx\approx[f(\overline{x}_1)+f(\overline{x}_2)+\cdots+f(\overline{x}_n)] \Delta x$$

بنابراین محاسبه تقریب سطح زیر منحنی که همان انتگرال معین تابع $$f(x)$$‌ در بازه $$[a,b]$$ است به شکل زیر در خواهد آمد.

$$\large \int_a^bf(x)dx\approx )\dfrac{(b-a)}{n}\sum_{i=1}^n f(\overline{x}_i)$$

این وضعیت در تصویری که در ادامه قابل مشاهده است به خوبی بیان شده.

گام چهارم: دریافت کامپایلر پایتون و ویرایشگر کد Canopy

در گام‌های اول تا سوم با شیوه محاسبه انتگرال و الگوریتم محاسباتی آشنا شدیم. در گام چهارم به بعد هم سعی داریم این الگوریتم را در پایتون پیاده‌سازی کنیم. البته برای شروع باید لوازم و ابزارهای مناسب در اختیارمان قرار گیرد. به عنوان ابزار کاری، احتیاج به یک کامپایلر پایتون به همراه یک ویرایشگر کد داریم تا دستورات مربوط به پیاده‌سازی الگوریتم را در ویرایشگر کد وارد کرده سپس با کامپایل کردن آن برنامه قابل استفاده شود. برای تهیه یک بسته مناسب از ویرایشگر و کامپایلر پایتون مراحل زیر را طی کنید.

• وارد این سایت (+) شوید.
• برنامه Canopy را بر روی رایانه خود بارگذاری (Download) کنید. البته برای این کار باید از نوع سیستم عامل خود مطالع باشید تا گزینه مناسب را برای بارگذاری Canopy انتخاب کنید.
• پس از بارگذاری و نصب برنامه، آن را اجرا کرده و گزینه Editor را از فهرست اصلی انتخاب کنید.
• با انتخاب گزینه create a new file یک پنجره کد در ویرایشگر Canopy باز خواهد شد.

از این نقطه به بعد می‌توانید کدهایی که در ادامه و گام‌های بعدی مشاهده خواهید کرد را در این پنجره وارد کنید.

گام پنجم: فراخوانی کتابخانه‌های مورد نیاز در پایتون و تعریف متغیرها

حال وقت و زمان کد نویسی فرا رسیده است. در بیشتر زمان‌هایی که برنامه‌ای با یک زبان برنامه‌نویسی ایجاد می‌کنید از متغیرها استفاده خواهید کرد. متغیر اسمی است که به یک یا مجموعه‌ای از مقدارها، نسبت داده می‌شود. ممکن است که این مقدارها توسط کاربر درون متغیرها قرار گیرند یا اینکه محاسبات درون برنامه مقادیر متغیرها را تعیین کند.

فیلم آموزش بهینه سازی با پایتون – بررسی و حل مسائل تحقیق در عملیات در فرادرس

کلیک کنید

در برنامه محاسبه انتگرال ما نیز از متغیرهایی با نام‌های a و b‌ و n استفاده خواهیم کرد. به این ترتیب، متغیرهای a و b کران‌های پایین و بالای انتگرال را به ترتیب بیان می‌کنند. همچنین n نیز تعداد تقسیمات برای فاصله بین a و b‌ را مشخص کرده است. البته انتخاب اسامی متغیرها می‌تواند به دلخواه برنامه‌نویس تغییر کند ولی در اینجا به علت هماهنگی با توضیحات گفته شده در گام‌های قبلی این نوع نام‌گذاری روی متغیرها صورت گرفته است.

مقدارهای مربوط به این متغیرها در طول اجرای برنامه از کاربر پرسیده می‌شوند. به این ترتیب بازه‌ای که باید انتگرال گرفته شود تعیین شده و مقدار n‌ نیز دقت محاسبه انتگرال را مشخص می‌کند. نوع مقدارهایی که در این متغیرها جای خواهد گرفت در اصطلاح برنامه‌نویسی type یا نوع نامیده می‌شود. در اینجا از دو نوع int به معنی عدد صحیحی (Integer) و float به معنی ممیز شناور (Floating Point) یا اعداد اعشاری (Decimal) استفاده شده است. مشخص است که باید n را از نوع int و a و b را از نوع float انتخاب کنیم.

نکته: کامپایلر از اجرای خطوطی از کد که با علامت # آغاز شده باشند منصرف می‌شود. معمولا این خطوط برای توضیحات در خلال کد نوشته می‌شوند تا منظور از نحوه محاسبه یا تعریف متغیرها برای خواننده واضح‌تر شود. بنابراین نگران تفسیر این خطوط در برنامه نباشید و آن‌ها را به عنوان راهنمای کد یا برنامه در نظر بگیرید.

1# -*- coding: utf-8 -*-
2# import math package to allow for more function arguments.
3from math import *
4# Here the parameters for numerical integration are defines.
5n = int(input("Enter how many times you want for sum (more times = more accurate):"))
6a= float(input("Enter the lower integration bound:  "))
7b= float(input("Enter the upper integration bound:  "))

همانطور که در کد بالا دیده می‌شود در قسمت اولیه کد، با فراخوانی و بارگذاری همه توابع موجود در کتابخانه math دسترسی به محاسبات انتگرال در پایتون فراهم می‌شود. بقیه خطوط نیز به تعریف متغیرها پرداخته است.

گام ششم: نوشتن یک تابع در پایتون به عنوان انتگرال‌ده

در این گام به معرفی تابعی می‌پرازیم که به عنوان انتگرال‌ده می‌شناسیم. این کار توسط کدی که در ادامه مشاهده می‌کنید صورت می‌پذیرد. توجه داشته باشید که تورفتگی‌هایی که در کد وجود دارد در زبان برنامه‌نویسی پایتون ضروری هستند و باید حتما رعایت شوند. در غیر اینصورت، امکان اجرا و مشاهده نتیجه محاسبات وجود نخواهد داشت. همچنین حروف بزرگ و کوچک در کدهای نوشته شده در پایتون یکسان تلقی نخواهند شد. بنابراین اگر value‌ را به شکل Value بنویسید، هنگام اجرای کد، ممکن است دچار خطا شوید.

1# This is the integration function which perform the integration named integrand
2def Integrate(n,a,b):
3    def f(x):
4# type your function after return
5        return x**2	
6    value=0
7    value2=0
8    for i in range (1, n+1):
9        value += f(a+((i-(1/2))*((b-a)/n)))
10    value2 = ((b-a)/n)*value
11    return value2

در بخش اول کد بالا، تابعی با نام Integrate معرفی شده که نتیجه انتگرال را محاسبه می‌کند به عنوان پارامتر برای این تابع متغیرهای n,a,b معرفی شده‌اند. ولی از آنجایی که این محاسبات احتیاج به یک انتگرال‌ده دارند در درون این تابع تابع دیگری با نام (f(x نیز دیده می‌شود. تعریف هر تابع به کمک دستور def صورت می‌گیرد. در کد بالا تابع مورد نظر به صورت $$f(x)=x^2$$ معرفی شده که در کد به شکل x**2 بعد از دستور return‌ دیده می‌شود. توجه داشته باشید که در پایتون توان با نماد ** مشخص می‌شود. اگر می‌خواهید تابع دیگری را به عنوان انتگرال‌ده معرفی کنید کافی است شکل محاسباتی آن را بعد از return وارد کنید. در گام نهم محاسبه انتگرال را برای تابع سینوس انجام خواهیم داد.

از طرفی محاسبه تابع در نقاط مربوط به مقدارهای میانی در متغیر value ثبت شده که شیوه محاسبه آن در فرمول‌های گام سوم دیده می‌شود. همچنین توسط یک حلقه تکرار نتیجه محاسبه برای سطح هر یک از مستطیل‌ها در value2 قرار می‌گیرد. در نتیجه مقدار نهایی برای value2، جواب انتگرال یا سطح زیر منحنی مربوط به تابع $$f(x)$$‌ است. حال باید نتیجه را به شکلی که لازم است در خروجی برنامه نمایش بدهیم. این مرحله در گام هفتم مورد بررسی قرار می‌گیرد.

گام هفتم: نمایش نتیجه محاسبه انتگرال

تا اینجا همه مراحل تعریف مسئله و راه‌حل انتگرال‌گیری ارائه شده است. تنها قسمت باقی‌مانده نمایش نتایج حاصل از اجرای الگوریتم است. یکی از موثرترین دستورات برای نمایش خروجی‌ها در زبان‌های برنامه‌نویسی استفاده از تابع Print است. کافی است که محتویاتی که باید نمایش داده شوند به عنوان پارامتر تابع Print به کار برید. در کدی که در ادامه قابل مشاهده است این کارها صورت گرفته. مشخص است که قبلا باید پارامترهای n, a, b وارد شده باشند تا محاسبات توسط تابع Integrate صورت گیرد و خروجی نمایش داده شود.

1# outputs including the integration value
2print("........................")
3print ("Here is your answer")
4print(Integrate(n,a,b))

نکته: علامت‌های .......... در دستور print به علت جداسازی ورودی‌های برنامه و خروج‌های ایجاد شده است. در گام بعدی نتیجه اجرای برنامه را مشاهده خواهید کرد.

گام هشتم: اجرای برنامه

به منظور اجرای این برنامه در محیط Canopy لازم است که از دکمه‌ای اجرا که در نوار ابزار توسط یک فلش سبز رنگ مشخص شده، استفاده کنید. پس از کامپایل موفق این برنامه و اجرا، پارامترهای مربوط به اجرای آن خط به خط از کاربر دریافت می‌شود. کافی است مقدار مناسب را برای هر یک از آن‌ها وارد کرده و نتایج را مشاهده کنید.

برای مثال فرض کنید که در سطر اول برای ورودی‌ها مقدار ۱۰۰۰۰ را برای n و کران پایین را در سطر دوم صفر وارد کنیم. با این کار مقدار a=0 خواهد بود. در ادامه در سطر سوم نیز اگر مقدار 1 وارد شود، بازه‌ای که باید انتگرال $$f(x)=x^2$$ در آن محاسبه شود به صورت $$[0,1]$$ خواهد بود. در عمل برنامه ما، انتگرال زیر را محاسبه خواهد کرد.

$$\large \int_0^{1}x^2dx$$

نتایجی که توسط دستور print ظاهر خواهند شد به صورت زیر خواهند بود.

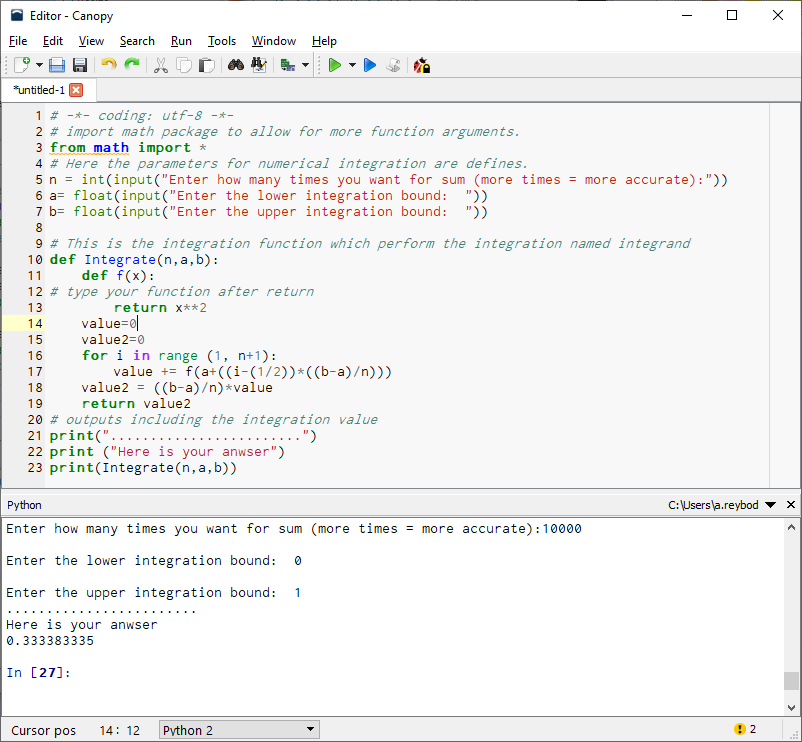
همانطور که دیده می‌شود مقدار این انتگرال در بازه $$[0,1]$$ براساس ده‌هزار نقطه برابر است با $$0.33338335$$ که به مقدار واقعی $$0.33333333$$ بسیار نزدیک است.

گام نهم: محاسبه انتگرال تابع سینوس

حال فرض کنید که قرار است مقدار انتگرال تابع سینوس را در بازه $$[0,2\pi]$$ محاسبه کنیم. ابتدا باید این تابع در بخش معرفی تابع مورد نظر در کد برنامه مشخص کنیم. همانطور که دیده می‌شود این کار باید درست بعد از اولین دستور return‌ صورت بگیرد. از طرفی هنگام اجرای برنامه نیز باید به کران‌ها اشاره کنیم. بنابراین کران پایین صفر a=0 و کران بالا با توجه به مقدار 3.1415 برای عدد $$\pi$$ برابر با 6.2832 خواهد بود. نتیجه اجرای این برنامه مطابق با تصویر زیر خواهد بود.

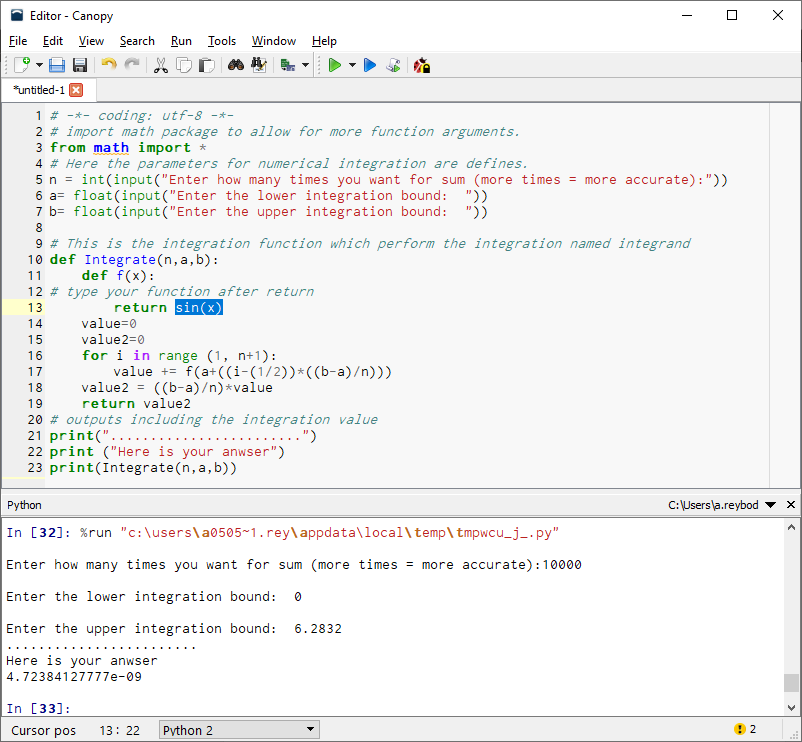
همانطور که دیده می‌شود مقدار پاسخ برابر با 4.72384127777e-09 خواهد بود که بسیار به صفر که مقدار واقعی برای این انتگرال محسوب می‌شود، نزدیک است.

گام دهم: توسعه برنامه

اینک به آخر کار برنامه محاسبه انتگرال رسیده‌ایم. فقط کافی است بیشتر با زبان برنامه‌نویسی پایتون آشنا شوید. برای مثال توابع به کار رفته در این برنامه بسیار ساده بودند و باید به صورت کاملا دستی، در برنامه نوشته شوند. می‌توان به کمک مقداری مهارت در برنامه‌نویسی شکل تابع نیز از کاربر دریافت شده و نمودار و سپس محاسبه انتگرال صورت گیرد. حتی می‌توانید با استفاده از یک «رابط تصویری» (Graphical User Interface یا GUI) برای درخواست پارامترها و نمایش خروجی‌ها استفاده کنید و برنامه کاملی داشته باشید. با انجام این کارها شاید بتوانید یک برنامه کاربردی تهیه کنید و در سایت خودتان قرار دهید تا محاسبات مربوط به انتگرال را برای کسانی که در این امر با مشکل مواجه هستند آسان کنید.

اگر به مباحث مرتبط در زمینه ریاضیات و برنامه‌نویسی علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌نویسی
• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های برنامه‌نویسی پایتون
• انتگرال به زبان ساده — بخش اول: مفاهیم
• مفاهیم، روش‌ های محاسبه و کاربردهای انتگرال — مجموعه مقالات وبلاگ فرادرس
• شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال‌ به روش عددی

^^