قضیه بین سینوس ها و کسینوس ها – فرمول ها + حل مثال
اگر در مثلثی اضلاع روبرو به سه زاویه و و را به ترتیب با و و نشان دهیم، در این صورت طبق قانون سینوسها رابطه و طبق قانون کسینوسها رابطه همیشه بین زاویهها و اضلاع این مثلث برقرار است. در این مطلب از مجله فرادرس توضیح میدهیم قضیه بین سینوس ها و کسینوس ها چیست. همچنین با حل چند نمونه سوال به شما کمک میکنیم تا به نحوه استفاده از این فرمولها کاملا مسلط شوید.
- یاد میگیرید قضیه سینوسها و کسینوسها چیست.
- با سه فرمول مختلف قانون کسینوسها آشنا میشوید.
- میآموزید که در چه شرایطی میتوان از قانون سینوسها در حل مسئله استفاده کرد.
- خواهید دانست که چگونه میتوان مجهولات یک مثلث را به کمک این قوانین بهدست آورد.
- خواهید آموخت که این دو قضیه در حل مسائل مکمل یکدیگراند.
- با حل چند نمونه سوال نحوه استفاده از فرمولهای این دو قانون را یاد میگیرید.

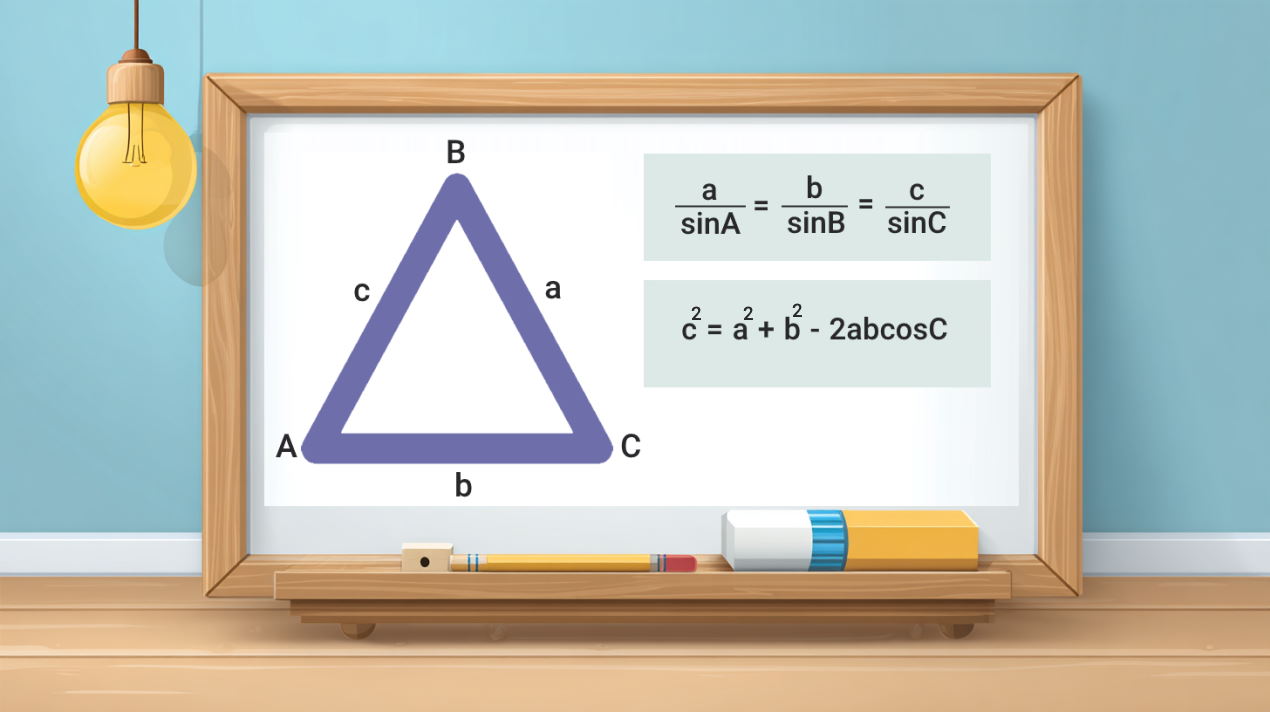
قضیه بین سینوس ها و کسینوس ها
مثلثی را به شکل زیر در نظر بگیرید که در آن ضلع روبرو به سه زاویه و و را برابر با و و در نظر گرفتهایم. طبق قانون سینوسها و کسینوسها همواره روابط و بین اضلاع و زاویههای این مثلث برقرار است. قضیه بین سینوس ها و کسینوس ها به ما کمک میکند تا بتوانیم تمام اضلاع و زاویههای یک مثلث را پیدا کنیم.
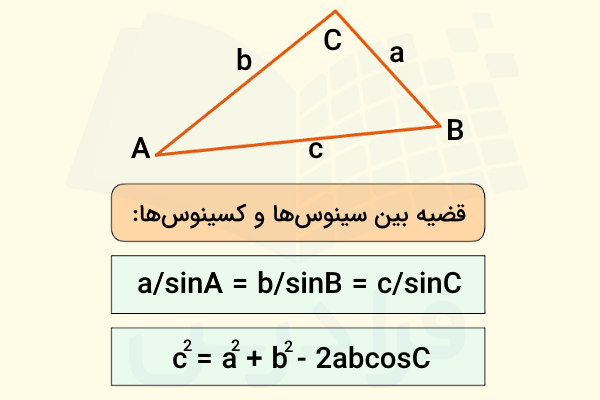
در مثلثهایی که قائمالزاویه نیستند، استفاده از قضیه فیثاغورس ابزار قدرتمندی نیست. در این شرایط قانون سینوسها با در نظر گرفتن نسبت یک ضلع به سینوس زاویه مقابل آن و قانون کسینوسها با بکارگیری شکل پیشرفتهتری از قضیه فیثاغورس به ما کمک میکنند تا با داشتن سه ضلع یک مثلث یا دو ضلع و زاویه بین آنها بتوانیم سایر اضلاع و زاویههای آن مثلث را پیدا کنیم. پس این دو قانون مکمل یکدیگراند، به این معنا که هرگاه نتوانیم از قانون سینوسها استفاده کنیم، میتوانیم قضیه کسینوسها را بنویسیم و برعکس.
برای مثال، اگر دو ضلع یک مثلث و زاویه بین آنها معلوم باشد، در این صورت نوشتن قانون سینوسها برای شروع محاسبه سایر اضلاع و زاویهها مناسب نیست، چون هیچکدام از سه نسبت کامل یعنی ضلع به سینوس زاویه مقابل آن را نداریم. پس در اینجا ابتدا قانون کسینوسها را برای پیدا کردن ضلع سوم مینویسیم و سپس برای پیدا کردن زوایای دیگر به سراغ قانون سینوسها میرویم تا محاسبات سادهتری داشته باشیم.
قانون کسینوسها مستقیما از تعریف ضرب داخلی دو بردار به دست میآید و قانون سینوسها را نیز میتوان از طریق فرمول مساحت مثلث و ضرب خارجی بردارها استخراج کرد. بنابراین ارتباط این دو فرمول در این است که هر دو بر مبنای ساختار فضای اقلیدسی و روابط حاکم بر طول و زاویه ایجاد شدهاند. همچنین با استفاده از رابطه بین سینوس و کسینوس یعنی میتوان ثابت کرد که این دو قانون کاملا با هم سازگاراند.
یادگیری سینوس و کسینوس با فرادرس
با یادگیری مفاهیمی مانند قضیه بین سینوس ها و کسینوس ها و روش به دست آوردن سینوس و کسینوس یک زاویه بر اساس جدول دایره مثلثاتی، میتوانید به راحتی مسائل پیچیدهتر را حل کنید. در همین زمینه، مشاهده فیلمهای آموزشی زیر از مجموعه فرادرس راهنمای جامعی برای یادگیری مثلثات محسوب میشود:
- فیلم آموزش رایگان سینوس، کسینوس و تانژانت + محاسبه نسبت های مثلثاتی فرادرس
- فیلم آموزش رایگان محاسبه مساحت مثلث با سینوس + مثال های مختلف فرادرس
- فیلم آموزش رایگان اثبات قضیه کسینوس ها + مثال فرادرس
- فیلم آموزش رایگان قضیه کسینوس ها و اثبات آن + مثال و کاربردها فرادرس
قضیه سینوس ها چیست؟
برای اینکه بتوانیم یک مثلث را حل کنیم و اضلاع و زاویههای مجهول آن را محاسبه کنیم، لازم است قضیه بین سینوسها و کسینوسها را بدانیم. در این بخش توضیح میدهیم قضیه بین سینوسها چیست، چگونه اثبات میشود و چه کاربردهایی دارد. مثلث را در نظر بگیرید که در آن زاویهها و ضلعهای روبروی هر کدام به شکل زیر نامگذاری شده است. قانون سینوسها برای این مثلث به شکل زیر است:
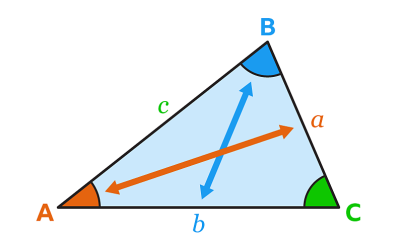
قانون سینوسها در حل چنین مثلثی زمانی به ما کمک میکند که یکی از دو حالت زیر را داشته باشیم:
- مقدار دو زاویه و اندازه یک ضلع معلوم باشد.
- اندازه دو ضلع و مقدار زاویهای که بین آن دو ضلع قرار نگرفته است، معلوم باشد.
همچنین اگر تمایل دارید با روش اثبات قانون سینوسها آشنا شوید، فرادرس یک فیلم رایگان با عنوان «فیلم آموزشی اثبات قضیه سینوس ها + مثالهای کاربردی» تهیه کرده است که لینک آن را در ادامه برای شما قرار دادهایم:
در ادامه با یک مثال عددی نشان میدهیم چگونه میتوان از این قانون در حل مسائل استفاده کرد. فرض کنید در مسئلهای حالت اول را داریم، یعنی مقدار دو زاویه و اندازه یک ضلع به شکل زیر معلوم است:
با توجه به اینکه میدانیم در تمام مثلثها مجموع زاویههای داخلی است، بنابراین زاویه سوم با کم کردن مجموع دو زاویه معلوم از به دست میآید:
از طرفی با توجه به شکل بالا میدانیم ضلع معادل است با . به این ترتیب حالا یکی از سه نسبت ما در قانون سینوسها کامل شده است:
و میتوانیم از آن برای به دست آوردن مقادیر و به شکل زیر استفاده کنیم:
قضیه کسینوس ها چیست؟
آموزش قضیه بین سینوس ها و کسینوس ها با یادگیری قانون کسینوسها کامل میشود. مجددا مثلثی که در بخش قانون سینوسها معرفی کردیم را در نظر بگیرید. قانون کسینوسها به ما کمک میکند تا بتوانیم طول یکی از سه ضلع این مثلث را با داشتن اندازه هر کدام از دو ضلع دیگر و زاویه بین آنها به شکل زیر محاسبه کنیم:

بنابراین قضیه کسینوسها سه فرمول مختلف دارد که در هر کدام میتوانیم یکی از سه ضلع هر مثلثی را پیدا کنیم. همچنین اگر طول هر سه ضلع را داشته باشیم، به کمک این فرمولها محاسبه هر سه زاویه امکانپذیر است. برای مثال، فرض کنید و و هستند. در این صورت طبق زاویه برابر میشود با:
با نوشتن سایر فرمولها سایر زاویهها به صورت و به دست میآیند. یک روش تست کردن درستی پاسخها این است که این سه زاویه را با هم جمع کنید:
همانطور که انتظار داریم این مجموع با مجموع زاویههای داخلی یک مثلث برابر شد.
حل مثال و تمرین از قضیه بین سینوس ها و کسینوس ها
در بخش آخر این مطلب از مجله فرادرس با حل چند نمونه سوال مختلف به شما کمک میکنیم تا به قضیه بین سینوس ها و کسینوس ها و نحوه استفاده از آن در حل مسائل کاملا مسلط شوید.
مثال ۱
اندازه در مثلث زیر چقدر است؟
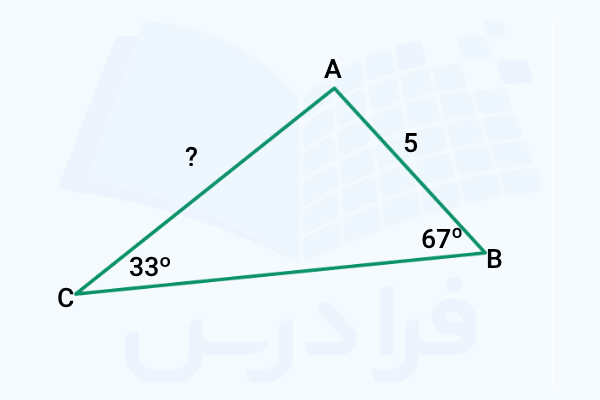
پاسخ
با توجه به اینکه اندازه یک ضلع را داریم و زاویه روبروی این ضلع و نیز داده شده است، بهترین روش برای پیدا کردن استفاده از قانون سینوسها به شکل زیر است:
مثال ۲
در مثلث زیر را محاسبه کنید:
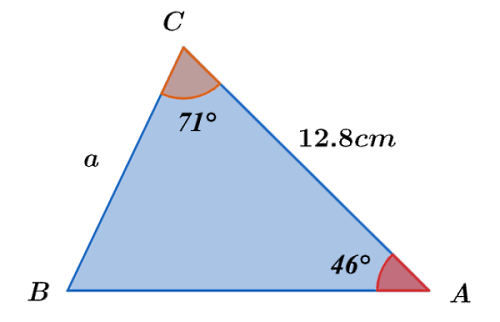
پاسخ
برای اینکه بتوانیم را پیدا کنیم، کافی است از قانون سینوسها استفاده کنیم. فقط باید توجه داشته باشیم که زاویه روبروی ضلع مشخص نیست، اما میتوان آن را با استفاده از دو زاویه دیگر به شکل زیر تعیین کرد:
مثال ۳
زاویه در یک مثلث چقدر است، اگر این زاویه بین دو ضلع و قرار گرفته باشد و ضلع سوم این مثلث نیز برابر با باشد:
پاسخ
در این سوال مقدار هیچ زاویهای را نداریم. پس نمیتوانیم از قانون سینوسها استفاده کنیم. اما با نوشتن فرمول قضیه کسینوسها به شکل زیر، پیدا کردن زاویه ممکن است. فقط باید دقت کنیم فرمولی را بنویسیم که در آن دو ضلع مجاور زاویه یعنی و در یک سمت و ضلع دیگر یعنی در سمت دیگر تساوی قرار بگیرد:
مثال ۴
در بسیاری از گوشیهای همراه مجهز به GPS پیش از اینکه سیگنال اصلی GPS دریافت شود، یک موقعیت مکانی تقریبی ارائه میشود. این کار از طریق فرآیندی به نام «تثلیث» (Triangulation) انجام میشود که با استفاده از فاصله گوشی تا دو نقطه مشخص یعنی دکلها کار میکند. فرض کنید دو دکل تلفن همراه در برد یک گوشی قرار دارند. این دو دکل در فاصله فوتی از یکدیگر و در امتداد یک بزرگراه مستقیم که مسیر آن شرق به غرب است، قرار گرفتهاند و گوشی تلفن همراه نیز در سمت شمال بزرگراه است. بر اساس تاخیر در رسیدن سیگنال، مشخص شده است که گوشی در فاصله فوتی از دکل اول و فوتی از دکل دوم قرار دارد. موقعیت تلفن همراه را در شمال و شرق دکل اول محاسبه کنید و مشخص کنید که این گوشی چقدر از بزرگراه فاصله دارد:
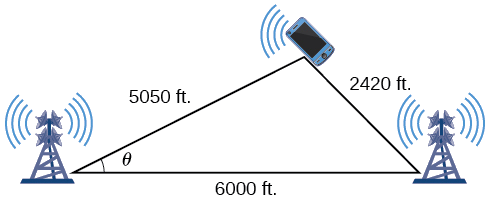
پاسخ
با استفاده از قانون کسینوسها میتوانیم مقدار زاویه را به دست آوریم. به خاطر داشته باشید که قانون کسینوسها از مربع یا توان دوم یک ضلع برای پیدا کردن کسینوس زاویه مقابل آن استفاده میکند. فرض کنید و و باشند. در نتیجه زاویه با ضلع مقابل خود یعنی متناظر است. به این ترتیب قانون کسینوسها به شکل زیر نوشته میشود:
برای پاسخ به سوال مربوط به موقعیت گوشی در شمال و شرق دکل و همچنین محاسبه فاصله آن تا بزرگراه، یک خط عمود از محل قرارگیری تلفن همراه مطابق تصویر زیر رسم میکنیم. این کار باعث ایجاد دو مثلث قائمالزاویه میشود. البته برای حل این مسئله ما فقط به آن مثلث قائمالزاویهای نیاز داریم که دکل اول در یکی از رئوس آن قرار دارد.
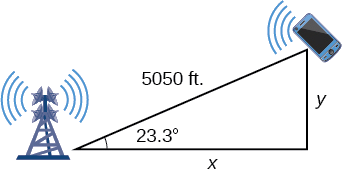
حالا با استفاده از زاویه و نسبتهای مثلثاتی پایه میتوانیم پاسخها را بیابیم:
بنابراین تلفن تقریبا در فاصله شرق و شمال اولین دکل و در فاصله از بزرگراه قرار دارد.
تمرین
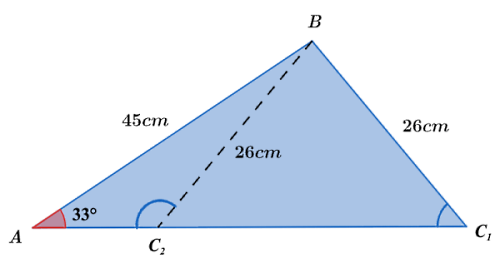
طبق تصویر زیر زاویههای و به ترتیب برابر با کدام گزینهاند؟
و
و
و
و
گزینه دوم صحیح است. زاویه به شکل زیر محاسبه میشود:
برای پیدا کردن باید دقت کنیم به اینکه مثلث سمت راست یک مثلث متساویالاضلاع است (دو ضلع برابر دارد). پس دو زاویه متناظر با این دو ضلع نیز برابر هستند. به این ترتیب از کم کردن از به دست میآید:
فرض کنید قایقی طبق شکل زیر از بندر خارج شده و مایل حرکت میکند. سپس درجه میچرخد و مایل دیگر را طی میکند. فاصله قایق از بندر چقدر است؟
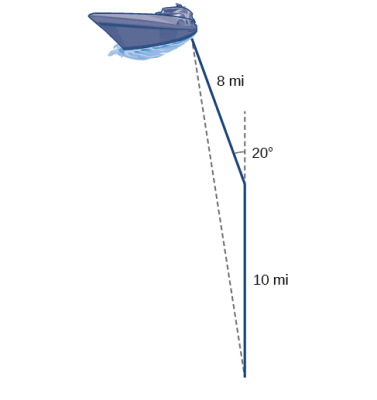
گزینه اول درست است. طبق صورت سوال، این قایق درجه چرخیده است. بنابراین یک زاویه باز (منفرجه) در مثلث غیرقائمالزاویه داریم که زاویه مکمل آن یعنی درجه خواهد بود. با داشتن این زاویه میتوانیم از قانون کسینوسها برای پیدا کردن ضلع مجهول مثلث یعنی همان فاصله قایق تا بندر استفاده کنیم:












