قانون هابل و ثابت هابل — به زبان ساده

ثابت هابل یکی از پارامترهای مهم کیهان شناختی است که با توجه به آن می‌توان یک مدل کیهان شناسی را رد یا تایید یا فاصله یک کهکشان تا ناظر را مشخص کرد. البته توجه به این نکته ضروری است که غیر از ثابت هابل پارامترهای دیگری نیز در رد یا تایید یک نظریه کیهان شناسی مهم هستند ولی در این مطلب در مورد اهمیت ثابت هابل در کیهان شناسی صحبت می‌کنیم. خواندن این مطلب به علاقه‌مندان نجوم و کیهان شناسی توصیه می‌شود.

قانون هابل چیست؟

واژه‌های جابه‌جایی قرمز و جابه‌جایی آبی به ترتیب به جابه‌جایی مشخصات طیفی قابل‌ شناسایی مانند خطوط طیفی به سمت طول موج‌های بلندتر یا کوتاهتر نسبت به طول موج‌هایی که به شکل طبیعی تحت شرایط استاندارد آزمایشگاهی قابل رصد هستند اشاره دارد.

یک راه تولید این تغییر خصوصیات، تاثیر داپلری ایجاد شده از حرکت یک منبع تابش نسبت به مشاهده کننده است. در چنین مواردی می‌توان از جابه‌جایی خطوط طیفی برای تعیین سرعتی که در آن ساطع کننده پرتو نوری نسبت به مشاهده کننده نزدیک يا دور می‌شود بهره برد.

به صورت کلی دلایل مختلفی برای تولید جابه‌جایی قرمز و جابه‌جایی آبی وجود دارد. طیف‌های کهکشان‌های دوردست جابه‌جایی قرمز را نمایش می‌دهند و همانگونه که در ادامه خواهید دید این جابه‌جایی‌های قرمز نتیجه تاثیرات داپلری نیستند و از تغییر در زمان بین ما و کهکشان‌ها ناشی می‌شوند.

جابه‌جایی قرمز در واقع به معنی افزايش فاصله بين ما و كهكشان است. مثالی شماتیک از جابه‌جایی قرمز در طیف یک کهکشان در شکل (1) نمایش داده شده است. در این مورد که نمونه‌ای مرسوم در کهکشان‌های دور دست است مقداری که هر خط طیفی دچار جابه‌جایی قرمز می‌شود با مقدار عددی z که می‌توان آن را جابه‌جایی قرمز خط دانست مشخص می‌شود (توجه داشته باشید که واژه جابه‌جایی قرمز در معنای پارامتر عددی z به شکل قراردادی در منابع انگلیسی و مرجع بدون خط فاصله نوشته می‌شود یعنی Red Shift و نه Red- Shift).

برای مشخص کردن جابه‌جایی قرمز z در یک مورد خاص تمام آنچه مورد نیاز است مقدار طول موج مشاهده شده $$\lambda_{obs}$$ از خطوط طیفی است که در نقطه تابش طول موج معین $$\lambda_{em}$$ دارند. به این ترتیب مقدار z را می‌توان از رابطه زیر بدست آورد:

$$z=\frac{\lambda_{o b s}-\lambda_{c m}}{\lambda_{e n}}=\frac{\lambda_{o b s}}{\lambda_{e m}}-1$$

به شکل کلی تمام خطوط طیفی که از یک کهکشان دوردست ایجاد می‌شوند به ميزان مشابهی جابه‌جایی قرمز پیدا می‌کنند. به همین دلیل جابه‌جایی قرمز هر خط ویژه در طیف یک کهکشان می‌تواند جابه‌جایی قرمز خود کهکشان محسوب شود. در موارد محدودی که طیف کهکشان جابه‌جایی آبی را به جای جابه‌جایی قرمز نشان می‌دهد رابطه بالا مقدار منفی z را می‌دهد. با در نظر گرفتن این مفهوم که جابه‌جایی آبی با مقدار منفی جابه‌جایی قرمز نمایش داده می‌شود در تمام این مطلب در مورد جابه‌جایی قرمز بحث خواهد شد.

پرسش: اکسیژن خطوط طیفی خود را در طول موج $$500.9$$ نانومتر ساطع می‌کند. با فرض اینکه این خطوط طیفی در یک کهکشان دیگر در طول موج $$596.1$$ نانومتر مشاهده شوند، جابه‌جایی قرمز کهکشان که از آن این خطوط ساطع می‏‌شوند چه قدر است؟

پاسخ: جواب به سادگی و با استفاده از رابطه بالا قابل محاسبه است و داریم:

$$z=\frac{(596.1-500.9) \mathrm{nm}}{500.9 \mathrm{nm}}=0.190$$

در اواخر دهه 1920 میلادی هنگامی که رصد و استفاده از داده‌های رصدی بسیار دشوار‌تر از زمان حال بود و تنها جابه‌جایی قرمز تعداد کمی از کهکشان‌ها اندازه‌گیری شده بود، هابل اندازه‌گیری مسافت تا کهکشان M31 یا همان آندرومدا را به همراه تعداد دیگری از کهکشان‌ها انجام داد. در سال 1929 او با استفاده از نتایج به دست آمده از 24 کهکشان اولین رابطه خطی بین جابه‌جایی قرمز و مسافت کهکشان‌ها را ارائه داد. در حال حاضر شکل کامل‌تر رابطه‌ای که هابل اعلام کرد به صورت زیر است و به عنوان قانون هابل شناخته می‌شود:

$$z=\frac{H_{0}}{c}d\quad (1)$$

که در آن c سرعت نور و $$H_{0}$$ ثابت است و با نام ثابت هابل شناخته می‌شود. دو جنبه مهم در رابطه جابه‌جایی قرمز- مسافت وجود دارد که لازم است به آن توجه شود.

اول آن که فرمول بالا تنها در مواردی که جابه‌جایی قرمز دامنه نسبتاً کوچکی (تا حدود $$0.2$$) دارد قابل استفاده است و در جابه‌جایی‌های قرمز که مقدار بیشتری دارند رابطه بین جابه‌جایی قرمز و مسافت بسیار پیچیده‌تر خواهد شد.

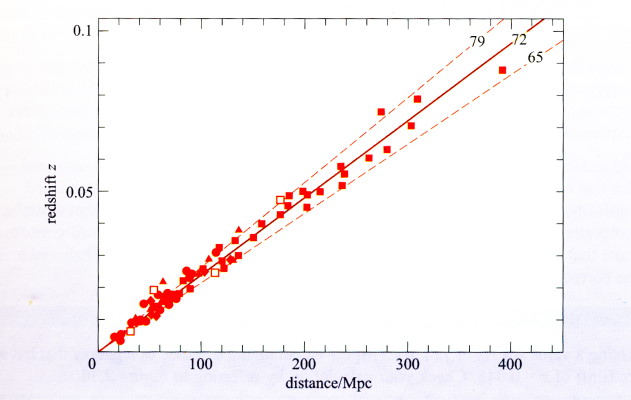
دوم این که حتی در جابه‌جایی‌های قرمز کوچک رابطه بین z و d همان گونه که در تصویر (2) نیز قابل مشاهده است، یک رابطه خطی کامل نخواهد بود. با این وجود رابطه (1) شکل استانداردی است از بیان آنچه در حال حاضر قانون هابل خوانده می‌شود.

قانون هابل معمولاً برای نشان دادن این موضوع که هستی در حال انبساط و گسترش است استفاده می‌شود که در ادامه آن را بررسی خواهیم کرد اما در این مرحله نشان دادن اینکه این رابطه چگونه به دست می‌آید مفید خواهد بود. رابطه بالا را می‌توان به صورت $$cz=H_{0}d$$ بازنویسی کرد.

پیش از این ذکر شد که به صورت کلی جابه‌جایی قرمز یک کهکشان و تاثیر داپلری آن ارتباطی با یکدیگر ندارند. اما در مواردی که جابه‌جایی قرمز به اندازه کافی کوچک باشد مقدار cz را می‌توان به عنوان سرعت رکود آن کهکشان تعریف کرد. به این ترتیب فرمول بالا را به شکل زیر بازنویسی می‌کنیم و داریم:

$$v=H_{0}d$$

بنابراین در این تفسیر سرعت رکود یک کهکشان متناسب با فاصله كهكشان با ما است. این موضوع تنها در عالمی که به شکل یکنواخت تحت انبساط قرار دارد اتفاق می‌افتد. در این حالت هر نقطه نسبت به سایر نقاط در حال جابه‌جایی خواهد بود و سرعت هر نقطه نسبت به تقطه دیگر متناسب با فاصله بین آن دو خواهد بود. در چنین عالمی که به شکل یکنواخت در حال انبساط است ثابت هابل بسیار پراهمیت خواهد بود زیرا كه سرعت انبساط کیهانی را مشخص می‌کند.

توجه داشته باشید با اینکه به صورت کلی تغییر مکان کهکشان‌ها نسبت به زمین رصد و ارزیابی می‌شود اما این موضوع بدان معنی نیست که زمین جای خاصی در هستی را اشغال کرده است. در یک هستی در حال انبساط به شکل یکنواخت هر نقطه نسبت به تمام نقاط دیگر در حال تغییر مکان است.

رابطه مسافت بر حسب سرعت اغلب در کتاب‌های ستاره شناسی و نجوم بیان می‌شود و در برخی موارد به اشتباه به عنوان قانون هابل در نظر گرفته می‌شود. در این مطلب به صورت قراردادی و پذیرفته شده قانون هابل رابطه‌ای بین جابجایی قرمز و مسافت است که این رابطه را در معادله (1) نمایش دادیم.

استفاده از قانون هابل

برخلاف کامل نبودن رابطه خطی نشان داده شده در معادله (1)، قانون هابل پتانسیل بسیار بالایی به عنوان یک روش در اندازه‌گیری مسافت کهکشان‌ها دارد. در حال حاضر جابه‌جایی قرمز به آسانی قابل اندازه‌گیری است و به نظر می‌رسد تعيین فاصله تا هر کهکشان با دانستن مقدار ثابت هابل $$H_{0}$$ چندان دشوار نباشد. البته تعیین $$H_{0}$$ از زمان کشف قانون هابل همواره یک مشکل عمده بوده است.

پرسش: در صورت دانستن مقدار ثابت هابل یا $$H_{0}$$ آن را در چه واحدی از SI نشان خواهید داد؟

پاسخ: z نسبتی از کمیت‌های مشابه است (طول موج) و بنابراین واحد ندارد. لذا $$H_{0}$$ باید واحدی مشابه$$\frac{c}{d}$$ داشته باشد. اگر از واحدهای SI استفاده کنیم آنگاه c (یعنی سرعت) دارای بُعد $$ms^{-1}$$ و d (یعنی مسافت) دارای بُعد m هستند و در نتیجه بُعد $$H_{0}$$ یا ثابت هابل $$s^{-1}$$ است.

با توجه به وجود واحدهای غیرمتعارف در نجوم و ستاره‌شناسی جای تعجب نیست اگر ستاره‌شناسان $$H_{0}$$ را در واحدهای SI بیان نکنند. معمولاً $$H_{0}$$ با واحد $$kms^{-1}Mpc^{-1}$$ بیان می‌شود. البته از آنجا که این واحدها سرعت را در هر واحد مسافت بیان می‌کنند جایگزین‌های معتبری برای $$s^{-1}$$ در SI هستند.

پیش از این ذکر شد که $$H_{0}$$ کمیت مهمی در کیهان شناسی است و در ادامه نشان خواهیم داد که این کمیت یکی از پارامترهایی است که خصوصیات هستی را شرح می‌دهد. در حال حاضر کافی است بدانیم مقدار $$H_{0}$$ در حدود $$72\ kms^{-1}Mpc^{-1}$$ تخمین زده شده است و تصور می‌شود این مقدار تنها در حدود $$10\%$$ خطا داشته باشد.

پرسش: با استفاده از مقدار $$72\ kms^{-1}Mpc^{-1}$$ برای $$H_{0}$$ فاصله کهکشانی را که جابه‌جایی قرمز آن $$z=0.048$$ است را محاسبه کنید و پاسخ خود را با توجه به شکل (2) بررسی کنید.

پاسخ: با بازنویسی معادله (1) داریم:

$$d=\frac{cz}{H_{0}}$$

حال با توجه به مقدار z و $$H_{0}$$ و قرار دادن این مقادیر در رابطه بالا داریم:

$$d=\frac{\left(3.00 \times 10^{5} \mathrm{kms}^{-1}\right) \times 0.048}{72 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}^{-1}}=200 \mathrm{Mpc}$$

در نتیجه با استفاده از قانون هابل فاصله این کهکشان تا ما 200 مگاپارسک است.

پرسش: اگر مقدار ثابت هابل $$H_{0}=72\ kms^{-1}Mpc^{-1}$$ باشد، مقدار آن در واحد SI یعنی بر حسب $$s^{-1}$$ چه قدر است؟

پاسخ: برای اینکه بتوانیم مقدار ثابت هابل را بر حسب واحدهای SI به دست آوریم باید سرعت را بر حسب $$ms^{-1}$$ و فاصله را بر حسب $$m$$ بیان کنیم و بدین ترتیب داریم:

$$H_{0}=72 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}^{-1}$$
$$H_{0}=7.2 \times 10^{4} \mathrm{~m} \mathrm{~s}^{-1} /\left(10^{6} \times 3.09 \times 10^{16} \mathrm{~m}\right)$$
$$H_{0}=2.33 \times 10^{-18} \mathrm{~s}^{-1}$$

بنابراین مقدار ثابت هابل بر اساس واحد SI برابر با $$2.33 \times 10^{-18} \mathrm{~s}^{-1}$$ است.

منشاء پراکندگی در رابطه بین جابه‌جایی قرمز و مسافت در قانون هابل بسیار حائز اهمیت است.

پرسش: اگر جدا از رابطه‌ای که در قانون هابل شرح داده شد کهکشان‌ها حرکات تصادفی نیز داشتند تاثیر آن بر نمودار جابه‌جایی قرمز- مسافت چگونه بود؟

پاسخ: حرکات تصادفی باعث تغییر مکان داپلری و در نتیجه دادن مقادیر مثبت و منفی به مجموع جابه‌جایی قرمز خواهد شد. به همین دلیل تاثیر حرکات تصادفی باعث ایجاد پراکندگی در رابطه فاصله و جابه‌جایی قرمز می‌شود.

از حرکت تصادفی کهکشان‎های منفرد گاهی با عنوان حرکات خاص یاد می‌شود. این عنوان به نحوی توضیحی برای پراکندگی در رابطه بین مسافت و جابه‎جایی قرمز است که در تصویر (2) نشان داده شده است. کهکشان‌های نزدیک به کهکشان راه شیری که در آن‌ها تاثیر انبساط هستی بر ثابت هابل قابل چشم‌پوشی است در فضا حرکتی معادل چند صد کیلومتر بر ثانیه دارند (در حقیقت این حرکات اغلب در نتیجه جذب کهکشان تحت تاثیر جاذبه نواحی بسیار چگال هستی اتفاق می‌افتد). هنگام استفاده از قانون هابل دانستن فاصله کهکشانی که در آن جابه‌جایی قرمز به سبب انبساط ثابت هابل به جابه‌جایی قرمز در اثر حرکات تصادفی می‌رسد مفید خواهد بود. این موضوع پرسشی است که در زیر مطرح شده است.

پرسش: اگر فرض شود کهکشان‌ها به عنوان مثال سرعت‌های تصادفی در حدود $$300 kms^{-1}$$ دارند. (الف) جابه‌جایی قرمز مورد انتظار برای کهکشان‌های مجاور را محاسبه کنید (یعنی کهکشان‌هایی که آنقدر نزدیک هستند که جابه‌جایی قرمز سیستماتیک پیش‌بینی شده برای آن‌ها توسط قانون هابل قابل چشم پوشی باشد) آیا مقدار این جابه‌جایی قرمز الزاماً مثبت خواهد بود؟ (ب) در چه مسافتی جابه‌جایی قرمز پیش بینی شده با استفاده از قانون هابل بر جابه‌جایی قرمز محاسبه شده در بخش (الف) برتری خواهد یافت؟ فرض کنید قانون هابل هنگامی که جابه‌جایی قرمز هابل ده برابر بزرگتر از جابه‌جایی قرمز به سبب حرکات تصادفی کهکشان‌ها باشد بر آن برتری می‌یابد و اینکه $$H_{0}=72\ kms^{-1}Mpc^{-1}$$ است.

پاسخ:

الف) جابه‌جایی قرمز به دلیل حرکات تصادفی را جابه‌جایی داپلری می‌گوییم. معادله‌ای که سرعت شعاعی و جابه‌جایی داپلری را به هم مربوط می‌کند به صورت زیر است:

$$v=c\left(\lambda_{\mathrm{obs}}-\lambda_{\mathrm{em}}\right) / \lambda_{\mathrm{cm}}$$

اما از طرفی داریم:

$$z=\left(\lambda_{\mathrm{obs}}-\lambda_{\mathrm{em}}\right) / \lambda_{\mathrm{cm}}$$

بنابراین $$v=cz$$ و $$z=\frac{v}{c}$$ است. اگر $$v=300kms^{-1}$$ باشد در نتیجه مقدار جابه‌جایی قرمز یا z برابر است با:

$$\begin{aligned} & z=\left(300 \times 10^{3} \mathrm{~m} \mathrm{~s}^{-1}\right) /\left(3.00 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}\right) \\ \text {i.e. } \quad & z=1.0 \times 10^{-3} \end{aligned}$$

همان طور که می‌بینید یک سرعت تصادفی معمولی باعث جابه‌جایی قرمز در حد $$0.001$$ می‌شود. از آنجا که حرکت تصادفی یک کهکشان می‌تواند به سمت ما و یا در حال دور شدن از ما باشد آن را به ترتیب با علامت منفی و مثبت نمایش می‌دهیم.

ب) فاصله‌ای که در آن جابه‌جایی قرمز هابل ده برابر بیشتر از جابه‌جایی قرمز حرکت تصادفی کهکشان‌ها باشد را می‌توان توسط قانون هابل به دست آورد. از قسمت (الف) جابه‌جایی قرمز حرکات تصادفی را $$0.001$$ به دست آوردیم. ده برابر این مقدار برای جابه‌جایی قرمز هابل برابر با $$z=10 \times 0.001=0.01$$ است. در نتیجه با استفاده از قانون هابل داریم:

$$d=\frac{c z}{H_{0}}$$
$$d=\frac{\left(3.00 \times 10^{5} \mathrm{~km} \mathrm{~s}^{-1}\right) \times 0.01}{72 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}^{-1}}=42 \mathrm{Mpc}$$

پاسخ به پرسش بالا نشان می‌دهد قانون هابل برای مسافت‌های اندازه‌گیری شده هنگامی که جابه‎جایی قرمز کمتر از $$0.01$$ باشد قابل اتکا نیست. این اندازه برابر است با فاصله‌ای در حدود 40 مگاپارسک و در زمانی است که ثابت هابل برابر با $$H_{0}=72\ kms^{-1}Mpc^{-1}$$ باشد.

ثابت هابل و مدل‌های کیهان شناسی

در مطالب قبلی در مورد مدل‌های کیهان شناختی صحبت کردیم. در ادامه مباحث نجوم و کیهان شناسی باید بدانیم هر مدل کیهان شناختی شامل معادلاتی است که روابط کلی بین مقادیر رصد شده را با پارامترهایی بیان می‌کند که قبل از این که توسط مدل کیهان شناسی مقدار آن‌ها مشخص شود توسط رصد به دست آمده‌اند.

در مدل‌هایی که تاکنون برای هستی ارائه شده است یک عبارت کلی وجود دارد که هندسه فضا-زمان را از نظر تفکیک وقایع توصیف می‌کند. نشان دادن شکل این معادله به یک کیهان شناس، برای اثبات این موضوع که هستی شرح داده شده توسط معادله همگن و ایزوتروپیک است کافی است. البته لازمه درک جزئیات خصوصیات هندسی فضا-زمان در چنین عالمی تعیین پارامترهايی مانند پارامتر خمیدگی یا k و ضریب مقیاس یا $$R(t)$$ است که در مدل به دست می‌آید. تنها هنگامی که در مدل کیهان شناسی این پارامترها تعیین شده باشند می‌توان کمیت‌هایی همچون خمیدگی فضا که در زمان t از رابطه $$\frac{k}{[R(t)]^{2}}$$ به دست می‌آید را محاسبه کرد.

در اهمیت پارامترهای رصدی می‌توان بر یادآوری این نکته تاکید کرد كه رفتار ضریب مقیاس را که می‌توان با معادله فریدمن معین کرد شامل مقادیر پارامتر خمیدگی یا k، ثابت کیهان شناختی یا $$R(t)$$ و چگالی متوسط ماده یا $$\rho$$ است. مقادیری که همه آن‌ها در اصل پارامترهای رصدی در هر زمان مشخص هستند.

این مطلب به پارامترهای برخاسته از مدل‌های FRW و ارتباط آن‌ها با پارامترهای رصدی (مانند ثابت هابل) مربوط می‌شود. با تعیین و استفاده از این روابط، استفاده از رصدهای نجومی برای تعیین اینکه کدامیک از مدل‌های کیهان شناختی به هستی واقعی نزدیک‌تر است، ممکن می‌شود. این موضوع یکی از چالش‌های اصلی شاخه‌ای از کیهان شناسی است که با نام کیهان شناسی رصدی شناخته می‌شود.

در این بخش به بررسی یکی از پارامترهای قابل اندازه‌گیری یعنی ثابت هابل در کیهان شناسی می‌پردازیم و تاکید اصلی بر روی روابط بین این پارامترها است و نه مقادیر آن‌ها. مقادیر پارامترهای قابل رصد و بهترین راه‌های تعیین آنها را سعی می‌کنیم در مطالب دیگری ذکر کنیم.

قانون هابل، ثابت هابل و پارامتر هابل

یکی از نتایج رصدی که توضیح بسیار طبیعی در زمینه کیهان شناسی فریدمن-رابرتسون-واکر یا FRW ارائه می‌دهد قانون هابل است. در حقیقت قانون هابل افزایش جابه‌جایی قرمز (یا z) یک کهکشان را متناسب با فاصله آن (یا d) از بیننده با معادله زیر توضیح می‌دهد:

$$z=\frac{H_{0}}{c}d \quad$$

که در آن ثابت تناسب یعنی $$\frac{H_{0}}{c}$$ برابر با ثابت هابل (یا $$H_{0}$$) تقسیم بر سرعت نور در خلاء (یا c) است. می‌توان برای هر کهکشان مشخص جابه‌جایی قرمز یا z در معادله بالا را به ترتیب به طول موج‌های رصد شده و تابش شده یعنی $$\lambda_{obs}$$ و  $$\lambda_{em}$$ مرتبط کرد. این ارتباط در معادله زیر مشخص شده است:

$$z=\frac{\lambda_{obs}-\lambda_{em}}{\lambda_{em}}$$

با اندازه‏‌گیری جابه‌جایی قرمز کهکشان‌های دور دست، اندازه‌گیری فاصله تا آن کهکشان‌ها به شکل جداگانه و استفاده از مقدار سرعت نور در خلاء که مقدار شناخته شده و ثابتی دارد، می‌توان از معادله (1) برای تعیین مقدار پارامتر هابل (یا $$H_0$$) استفاده کرد.

همان طور که گفتیم سال‌ها پیش «ادوین هابل» (Edwin Hubble) نیز این کار را انجام داد اما نتایجی که به دست آورد به دلیل داده‌های اولیه نادرست و غیردقیق، صحیح نبود. رصدهای جدید و مدرن امکان محاسبه ثابت هابل را تنها با ميزان خطای $$10\%$$ فراهم کرده‌اند و به مرور روش‌هايی برای كاستن این مقدار خطا در حال توسعه است. تخمین جدید از مقدار ثابت هابل عبارت است از :

$$H_{0}=(2.3 \pm 0.3) \times 10^{-18} \mathrm{~s}^{-1}$$

البته به دلايل تاریخی این مقدار را معمولاً در واحد $$km s^{-1}Mpc^{-1}$$ (یعنی کیلومتر بر ثانیه بر مگاپارسک) بیان می‌کنند یعنی داریم:

$$H_{0}=(72 \pm 8) \mathrm{km} \mathrm{s}^{-1} \mathrm{Mpc}^{-1}$$

$$H_{0}$$ یکی از مهمترین پارامترهای رصدی در کیهان شناسی است. اما این پارامتر چگونه به مدل‌های FRW از هستی در حال انبساط ارتباط پیدا می‌کند در حالی که آشکارترین پارامترها در این مدل‌ها k و $$R(t)$$ هستند و $$H_{0}$$ در این معادلات دیده نمی‌شود؟ این موضوعی است که در ادامه به آن خواهیم پرداخت.

رابطه ثابت هابل با مدل فریدمن-رابرتسون-واکر

شکل (3) اساس ارتباط ثابت هابل با یکی از مدل‌های کیهان شناسی یعنی FRW را نمایش می‌دهد. این شکل دو تصویر از عالم FRW در حال انبساط را با ضریب مقیاس $$R(t)$$ در دو زمان مختلف نشان می‌دهد.

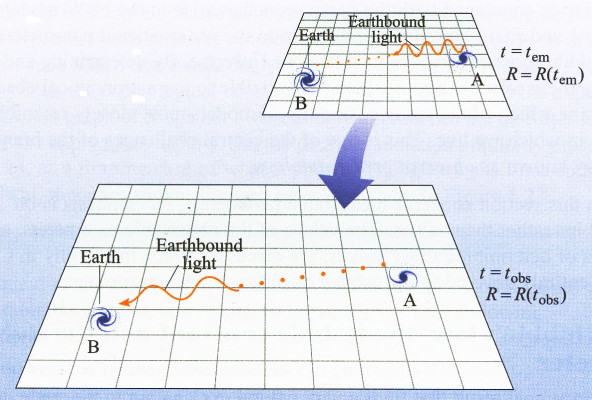
در این تصویر دو کهکشان A و B به صورت تصادفی بر روی مختصات یک عالم در حال انبساط در نظر گرفته شده‌اند. تصویر اول معرف زمان $$t_{em}$$ است که در آن یک باریکه نور از کهکشان A ساطع شده است و تصویر دوم نیز معرف زمان $$t_{obs}$$ است که در آن همان نور در کهکشان B رصد شده است.

هنگامی که پرتو نور در حال حرکت از کهکشان A به B است مختصات دو کهکشان تغییر نمی‌کند اما فاصله فیزیکی بین دو کهکشان به این دلیل که فاصله فیزیکی متناسب با ضریب مقیاس یا $$R(t)$$ است تغییر می‌کند. در حقیقت ضریب مقیاس در زمان رسیدن نور به کهکشان B یعنی $$R(t_{obs})$$ بزرگتر از ضریب مقیاس در زمان ساطع شدن نور یعنی $$R(t_{em})$$ است. فاصله بین دو کهکشان A و B در زمان $$t_{em}$$ هرچه باشد با نسبت $$\frac{R(t_{obs})}{R(t_{em})}$$ در زمان $$t_{obs}$$ افزایش خواهد یافت. حال این ضریب انبساط یعنی $$\frac{R(t_{obs})}{R(t_{em})}$$ معرف رشد خود فضا خواهد بود و بنابراین بر طول موج نوری که آزادانه بین دو کهکشان در حال حرکت است نیز تاثیر خواهد گذاشت. در نتیجه نوری که در زمان $$t_{em}$$ و با طول موج $$\lambda_{em}$$ از A ساطع شده است در زمان $$t_{em}$$ و با طول موج بلندتر $$\lambda_{\mathrm{obs}}=\lambda_{\mathrm{em}} \times R\left(t_{\mathrm{obs}}\right) / R\left(t_{\mathrm{em}}\right)$$ در کهکشان B رصد می‌شود. این افزایش در طول موج را ناظر در کهکشان B به شکل جابه‌جایی قرمز خواهد دید .

پرسش: برای یک مشاهده کننده در کهکشان B در زمان $$t_{obs}$$ جابه‌جایی قرمز کهکشان A چقدر است؟ پاسخ خود را براساس ضریب انبساط $$R\left(t_{\mathrm{obs}}\right) / R\left(t_{\mathrm{em}}\right)$$ ارائه دهید.

پاسخ: با استفاده از معادله $$z=\frac{\lambda_{obs}-\lambda_{em}}{\lambda_{em}}$$ و بازنویسی آن داریم:

$$z=\frac{\lambda_{\mathrm{obs}}-\lambda_{\mathrm{em}}}{\lambda_{\mathrm{em}}}=\frac{\lambda_{\mathrm{em}}\left[\left(\lambda_{\mathrm{obs}} / \lambda_{\mathrm{em}}\right)-1\right]}{\lambda_{\mathrm{em}}}$$

با ساده کردن $$\lambda_{em}$$ از صورت و مخرج معادله بالا خواهیم داشت:

$$z=\frac{\lambda_{obs}}{\lambda_{em}}-1$$

با جایگزین کردن $$\frac{\lambda_{obs}}{\lambda_{em}}$$ با مقدار معادل ضریب انبساط آن یعنی $$\frac{R_{t_{obs}}}{R_{t_{em}}}$$ نیز داریم:

$$z=\frac{R\left(t_{\mathrm{obs}}\right)}{R\left(t_{\mathrm{em}}\right)}-1$$

توجه داشته باشید که بر اساس مدل‌های FRW جابه‌جایی قرمز یک کهکشان دور دست اساساً به دلیل انبساط فضا رخ می‌دهد و انبساط عالم تاثیری بر جابه‌جایی داپلری ندارد. اینگونه جابه‌جایی‌های قرمز که به دلیل انبساط فضا رخ می‌دهند را برای متمایز کردن از مواردی که تحت تاثیر جابه‌جایی داپلری حاصل می‌شوند جابه‌جایی‌های قرمز کیهان شناختی نامگذاری کرده‌اند. البته کهکشان‌های واقعی مانند کهکشان‌های ایده‌آل که در تصویر (2) نمایش داده شده است رفتار نخواهند کرد. کهکشان‌های واقعی ممکن است نوعی حرکات غیرعادی نیز از خود نشان دهند که می‌تواند به دلیل جابه‌جایی داپلری باشد. همین اثر داپلری است که سبب می‌شود جابجایی قرمز رصد شده کهکشان‌ها با جابه‌جایی قرمز کیهان شناختی آن‌ها تفاوت داشته باشد.

در پرسش قبل دیدیم که چگونه جابه‌جایی قرمز می‌تواند از انبساط در مدل فریدمن -رابرتسون -واکر حاصل شود اما نکته اصلی قانون هابل این است که جابه‌جایی قرمز (یا z) یک کهکشان دوردست متناسب با فاصله آن افزایش می‌یابد.

موضوع اصلی این است که ارتباط مدل‌های FRW به قانون هابل چیست؟ در جواب این پرسش باید گفت هر چه فاصله تا کهکشان بیشتر باشد نور زمان بیشتری لازم دارد تا از آن کهکشان به ما برسد، هرچه فاصله بین زمان تابیده شدن تا زمان رصد شدن بیشتر باشد ضریب انبساط یعنی $$\frac{R_{t_{obs}}}{R_{t_{em}}}$$ بیشتر خواهد بود و به همین دلیل جابجایی قرمز نور یعنی $$\frac{R_{t_{obs}}}{R_{t_{em}}}-1$$ بزرگتر است.

این استدلال پیرامون مدت زمان سفر نور در فضا تفسیری کیفی از قانون هابل در یک مدل در حال انبساط FRW ارائه می‏‌دهد اما طبیعت آشکار مدل‌های FRW این امکان را ایجاد می‌کند که حتی بسیار دقیق‌تر به ماهیت این ارتباط پرداخت. همچنین این امکان وجود دارد که معادله‌ای به دست آورد که ثابت هابل را به ضریب مقیاس مرتبط کند. برای این منظور دو کهکشان را که با فاصله نسبتاً کوچک d در زمان t از یکدیگر قرار دارند را در نظر بگیرید. در این حالت پارامتر مقیاس $$R(t)$$ است. به دلیل این که این دو کهکشان به یکدیگر نزدیک هستند زمان سپری شده توسط نور برای رسیدن از یکی به دیگری یعنی $$\frac{d}{c}$$ نیز کوتاه است و با $$\Delta(t)$$ نمایش داده می‌شود. با استفاده از معادله $$z=\frac{R\left(t_{\mathrm{obs}}\right)}{R\left(t_{\mathrm{em}}\right)}-1$$ جابه‌جایی قرمز رصد شده یکی از این کهکشان‌ها هنگامی که از کهکشان دیگر نگریسته شود برابر است با:

$$z=\frac{R(t+\Delta t)}{R(t)}-1$$

به دلیل انبساط عالم $$R(t+\Delta t)$$ از $$R(t)$$ بزرگتر است. این موضوع را می‌توان به شکل زیر نیز نمایش داد:

$$R(t+\Delta t)=R(t)+\Delta R(t)$$

که در آن کمیت جدید $$\Delta R(t)$$ نشان‌ دهنده افزایش اندک در ضریب مقیاس است که در زمان کوتاه $$\Delta t$$ رخ می‌دهد. توجه داشته باشید $$\Delta R(t)$$ معرف یک کمیت منفرد است و حاصل ضرب کمیت‌هايی مانند $$\Delta$$ و $$R(t)$$ نيست. با جایگزین کردن $$R(t+\Delta t)$$ با $$R(t)+\Delta R(t)$$ در معادله $$z=\frac{R(t+\Delta t)}{R(t)}-1$$ داریم:

$$z=\frac{R(t)+\Delta R(t)}{R(t)}-1$$

این معادله را می‌توان به شکل زیر بازنویسی کرد:

$$z=1+\frac{\Delta R(t)}{R(t)}-1$$

که در نتیجه داریم:

$$z=\frac{\Delta R(t)}{R(t)}$$

 $$\Delta R(t)$$ یعنی تغییر در ضریب مقیاس که در فاصله زمانی کوتاه $$\Delta t$$ رخ می‌دهد برابر با حاصلضرب بازه زمانی $$\Delta t$$ در سرعت تغییر R در زمان t خواهد بود. مثال ملموس این موضوع مانند این است که بگوییم در طول زمان $$\Delta t$$ ماشینی که با سرعت $$v$$ حرکت می‌کرده به اندازه $$\Delta t \times v$$ جابه‌جا شده و $$v$$ سرعت تغییر در مکان جسم است.

به شکل قراردادی سرعت تغییر ضریب مقیاس در زمان t را با $$\dot{R}(t)$$ نمایش می‌دهیم، بنابراین $$\Delta R(t)=\Delta t\times \dot{R}(t)$$ خواهد بود و داریم:

$$z=\frac{\Delta t\times \dot{R}(t)}{R(t)}$$

صورت و مخرج معادله بالا را در $$c$$ ضرب می‌کنیم و معادله را به صورت زیر بازنویسی می‌کنیم:

$$z=\frac{c\Delta t}{c}\times \frac{\dot{R}(t)}{R(t)}$$

$$z=\frac{1}{c}\times \frac{\dot{R}(t)}{R(t)}\times d$$

در رابطه بالا $$d$$ فاصله بین دو کهکشان است. اگر رابطه (2) را با رابطه بالا مقایسه کنیم می‌توانیم نتیجه بگیریم که تساوی زیر برقرار است:

$$H(t)=\frac{\dot{R}(t)}{R(t)}$$

در حقیقت در معادله بالا ثابت هابل را با توجه ضریب مقیاس به دست آورده و همچنین رابطه مشخصی بین ثابت هابل و مدل فریدمن- رابرتسون- واکر به دست آوردیم.

مقدار پارامتر هابل در رابطه بالا با زمان تغییر می‌کند اما دقیق‌تر این است که بگوییم پارامتر هابل با تغییر $$R(t)$$ در زمان تغییر می‌کند و به همین دلیل مقدار آن از یک مدل FRW به مدل دیگر تفاوت خواهد داشت.

بدین ترتیب با ارزیابی پارامتر تئوری هابل در زمان $$t_{0}$$ و مقایسه آن با مقدار رصدی ثابت هابل می‌توان متوجه شد که آیا مدلی که در حال بررسی آن هستیم توصیف درستی از عالم ارائه می‌دهد یا خیر؟ اگر مقدار به دست آمده از نظر تئوری و رصدی با یکدیگر برابر باشند یعنی مدل مورد بحث یکی از شرایطی که به عنوان یک مدل کیهان شناسی مورد قبول قرار بگیرد را دارد.

$$H(t_{0})=\frac{\dot{R}(t_{0})}{R(t_{0})}=H_{0}$$

همانگونه که گفته شد با استفاده از معادله بالا ارتباط بین پارامتر رصدی $$H_{0}$$ با ضریب مقیاس $$R(t)$$ در مدل FRW برقرار می‌شود.

$$\dot{R}(t)$$ در واقع معرف سرعت تغییر R در زمان t است. بنابراین در حقیقت $$\frac{\dot{R}(t)}{R(t)}$$ سرعت نسبی تغییر ضریب مقیاس را نشان می‌دهد. با استفاده از این مفهوم می‌توان گفت در کیهان شناسی فریدمن- رابرتسون- واکر ثابت هابل معرف سرعت نسبی تغییر در ضریب مقیاس است که در زمان $$t_{0}$$ معین شده است. به شکل مختصر می‌توان گفت که در واقع ثابت هابل رصد شده مقدار فعلی پارامتر هابل در مدل کیهان شناسی است.

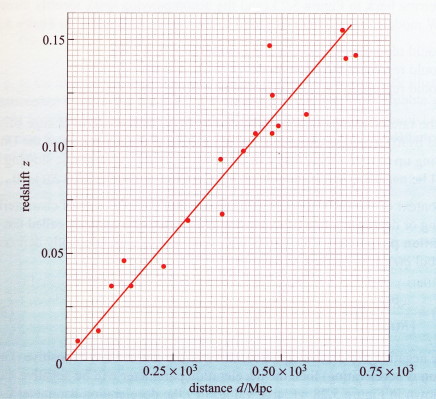
پرسش: شکل (4) نمودار جابه‌جایی قرمز بر حسب مسافت برای تعدادی کهکشان را نمایش می‌دهد. این نمودار شامل خط بهینه ترسیم شده از میان تمامی داده‌ها است. با فرض اینکه هستی ما به خوبی با مدل در حال انبساط فریدمن- رابرتسون- واکر مطابقت داشته باشد اهمیت شیب خط این نمودار را ذکر کرده و مقدار این شیب را از نمودار به دست آورید و سپس مقدار ثابت هابل را تعیین کنید.

پاسخ: این خط بهینه با قانون هابل به صورت زیر تعریف می‌شود:

$$z=(\frac{H_0}{c})d$$

بنابراین شیب خط در تصویر (4) برابر با $$\frac{H_{0}}{c}$$ یعنی حاصل تقسیم ثابت هابل بر سرعت نور در خلاء است. شیب یک خط راست را می‌توان به راحتی از رابطه تغییرات مقادیر در راستای y نسبت به تغییرات مقادیر در راستای x به دست آورد و داریم:

$$\frac{H_{0}}{c}=\frac{\Delta z}{\Delta d}=\frac{0.15}{0.64 \times 10^{3} \mathrm{Mpc}}=2.34 \times 10^{-4} \mathrm{Mpc}^{-1}$$

در نتیجه ثابت هابل برابر است با:

$$\begin{aligned} H_{0} &=3.00 \times 10^{5} \mathrm{~km} \mathrm{~s}^{-1} \times 2.34 \times 10^{-4} \mathrm{Mpc}^{-1} \\ \text {i.e. } \quad H_{0} &=70 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}^{-1} \end{aligned}$$

توجه کنید که نمودار داده شده براساس داده‌های واقعی نیست و داده‌ها غیر واقعی هستند.

پرسش: سرعت تغییرات R در مدل اينشتين چه قدر است؟ این پاسخ چه چیز را در مورد پارامتر هابل در مدل اینشتین می‌رساند؟

پاسخ: در مدل اینشتین R با زمان تغییر نمی‌کند و بنابراین $$\dot{R}$$ در همه زمان‌ها برابر با صفر است. این بدین معنی است که در مدل اینشتین در همه زمان‌ها ثابت هابل برابر صفر است و در نتیجه $$H(t)=0$$. اینشتین مدل خودش را قبل از کشف قانون هابل معرفی و اعلام کرد و بدین دلیل در مدل خود نیازی به توضیح جهان در حال انبساط احساس نمی‌کرد.

نتیجه گیری

در این مطلب در مورد یکی از پارامترهایی که توسط کیهان شناسی رصدی قابل اندازه‌گیری است صحبت کردیم. در ابتدا قانون و ثابت هابل را معرفی کردیم و در مورد جابه‌جایی قرمر و آبی کهکشان‌ها و رابطه آن‌ها با فاصله یک کهکشان تا ناظر صحبت کردیم.

همچنین بیان کردیم که مقدار ثابت هابل در رد یا تایید یک مدل کیهان شناسی مهم است و با مقایسه مقدار به دست آمده رصدی ثابت هابل و مقداری که از یک مدل کیهان شناسی به دست می‌آید می‌توان در مورد رد یا تایید یک مدل کیهان شناسی صحبت کرد. هر چند غیر از ثابت هابل پارامترهای دیگری برای تایید یا رد یک مدل کیهان شناسی مهم هستند که در مطالب بعدی آن‌ها را بررسی خواهیم کرد.

سپس رابطه بین ثابت هابل را با مدل فریدمن- رابرتسون- واکر به دست آوردیم و نشان دادیم که ثابت هابل چگونه با ضریب مقیاس در مدل FRW مرتبط است. همچنین ثابت هابل را برای تایید و یا رد مدل کیهانی اینشتین نیز استفاده کردیم که این مقایسه نشان داد در مدل اینشتین ثابت هابل برابر با صفر است و دلیل این موضوع این است که اینشتین مدل کیهان شناسی خود را قبل از کشف هابل ارائه داد و در مدلش نیازی به در نظر گرفتن انبساط عالم را احساس نمی‌کرد.