ذره آزاد در مکانیک کوانتومی — به زبان ساده

در این مقاله در نظر داریم تا با زبانی ساده به تحلیل ذره آزاد (Free Particle) به وسیله معادله دیفرانسیلی شرودینگر بپردازیم. ذره آزاد در فیزیک، ذرهای است که تحت تاثیر هیچ نیروی خارجی نباشد. به عبارت دیگر، اگر ذرهای در محیطی با پتانسیل ثابت یا صفر قرار داشته باشد، به آن ذره آزاد گفته میشود.
از نقطه نظر فیزیک کلاسیک، اگر ذره در مکانی بدون حضور میدان باشد، ذره آزاد تلقی شده که تنها دارای انرژی جنبشی $$K$$ و تکانه $$P$$ است. از نقطه نظر مکانیک کوانتومی، اگر پتانسیل محیط ثابت باشد، ذره را آزاد تلقی میکنند. در مکانیک کوانتومی اغلب این پتانسیل ثابت را جهت راحتی کار، صفر در نظر میگیرند. در ادامه این مقاله با ما همراه باشید.
ذره آزاد
در مقاله «معادله شرودینگر -- به زبان ساده» با نحوه به دست آوردن معادله شرودینگر آشنا شدیم. معادله شرودینگر، معادله دیفرانسیلی است که حالت و وضعیت ذرات را به صورت موجی توصیف میکند. این امواج اصطلاحاً به امواج ماده (Matter Wave) موسوم هستند.
در مقاله مذکور دیدیم که دوبروی به هر ذرهای که دارای تکانه $$p$$ بود، موجی به طول موج λ نسبت داد. طول موج دوبروی برابر با مقدار زیر است:
$$\large \lambda = \frac{h}{p}$$
(1)
$$\large k = \frac{2 \pi}{\lambda}$$
(2)
در عبارت فوق، $$k$$ عدد موج است. در واقع با توجه به طول موج دوبروی، ذرهای نظیر یک الکترون را میتوان به صورت یک موج در نظر گرفت. حال فرض کنید که ذرهای در فضایی با پتانسیل ثابت قرار دارد. در مکانیک کوانتومی میتوانیم این پتانسیل ثابت را جهت راحتی کار، صفر تلقی کنیم. در ادامه این مقاله در نظر داریم تا این ذره آزاد را توسط معادله شرودینگر در یک بعد، تحلیل کنیم. مسئله ذره آزاد یکی از مهمترین و البته سادهترین مسائل جهت آموزش مفاهیم فیزیک و مکانیک کوانتومی است.
معادله شرودینگر در یک بعد به صورت زیر است:
$$\large - \frac{\hbar^{2}}{2m} \frac{d^{2} \psi (x)}{d x^{2}} + V(x) \psi (x) = E \psi (x)$$
(3)
با توجه به اینکه ذره آزاد است، پتانسیل را صفر در نظر میگیریم. در نتیجه:
$$\large V(x) = 0\ \Rightarrow\ - \frac{\hbar^{2}}{2m} \frac{d^{2} \psi (x)}{d x^{2}} = E \psi (x)$$
(4)
از مباحث فیزیک پایه میدانید که انرژی کل، برابر با جمع انرژی پتانسیل و انرژی جنبشی است ($$E = K + V$$). در اینجا به دلیل صفر بودن انرژی پتانسیل، انرژی کل تنها برابر با انرژی جبنشی است. توجه داشته باشید که در اینجا ذره آزاد غیرنسبیتی بوده و میتوان انرژی جنبشی آن را به فرم آشنای زیر نوشت:
$$\large V(x) = 0 \Rightarrow E = V + K = K = \frac{ 1 }{ 2 } m v^{ 2 } = \frac{ p^{ 2 } }{ 2 m }$$
(5)
با توجه به رابطه تکانه، طول موج و عدد موج (رابطه دوبروی - معادله ۱ و ۲) از رابطه فوق نتیجه میشود:
$$\large p = \frac{h}{\lambda}\ \ ,\ \hbar = \frac{h}{2 \pi}\ \ , \ k = \frac{2 \pi}{\lambda}\ \Rightarrow\ k^{2} = \frac{2 m E}{\hbar^{2}}$$
(6)
با توجه به رابطه فوق، معادله (4) به فرم ساده زیر در میآید:
$$\large \frac{d^{2} \psi (x)}{d x^{2}} + k^{2} \psi (x) = 0$$
(7)
جواب عمومی معادله دیفرانسیل فوق، به صورت ترکیب خطی از دو موج صفحهای به شکل زیر است:
$$\large \psi_{k} (x) = A_{+} e^{ikx} + A_{-} e^{-ikx}$$
(8)
در عبارت فوق، دو پارامتر $$A_{ + }$$ و $$A_{ - }$$ ثابتهایی دلخواه هستند. توجه داشته باشید که معادله (7) تنها بخش مکانی معادله شرودینگر را شامل میشود. در واقع موج $$\psi_{k} (x)$$ از حل معادله شرودینگر مستقل از زمان به دست آمده است.
اضافه کردن ترم زمانی به معادله فوق کار بسیار سادهای است. در مقاله «معادله شرودینگر» دیدیم که مولفههای زمانی و مکانی قابل تفکیک بوده و میتوان آن را به صورت زیر نوشت:
$$\large \Psi (x,t) = \psi (x) e^{- \frac{i E t}{\hbar}}$$
(9)
از مباحث فیزیک مدرن میدانیم که میتوان انرژی را به صورت $$E = hf$$ نوشت. این انرژی برحسب فرکانس زاویهای ω به صورت $$E = \hbar \omega$$ است که در آن $$\hbar$$ به ثابت پلانک کاهش یافته موسوم است و برابر با $$\frac{h}{2 \pi}$$ است. در نتیجه:
$$\large \Psi (x,t) = \psi (x) e^{-i \omega t}$$
(10)
با توجه به رابطه فوق، معادله (8) به فرم زیر در میآید:
$$\large \Psi_{k} (x,t) = (A_{+} e^{ikx} + A_{-} e^{-ikx}) e^{-i \omega t}$$
(11)
در نتیجه تابع موج توصیف کننده یک ذره آزاد به صورت زیر است:
$$\large \Psi_{k} (x,t) = \Psi_{+} (x,t) + \Psi_{-} (x,t) = A_{+} e^{i (kx - \omega t)} + A_{-} e^{- i (kx + \omega t)}$$
(12)
جمله $$\Psi_{+} (x,t) = A_{+} e^{i (kx - \omega t)}$$ بیانگر موجی است که به سمت راست و جمله $$\Psi_{-} (x,t) = A_{-} e^{i (kx + \omega t)}$$ بیانگر موجی است که به سمت چپ میرود.
به عبارت دیگر تابع موج $$\Psi (x,t)$$ که متشکل از دو موج $$\psi_{+} (x,t)$$ و $$\psi_{-} (x,t)$$ است، موج منتسب به ذرهای را توصیف میکند که با تکانه (ممنتوم) و انرژیِ خوش تعریفِ $$p_{\pm} = \pm \hbar k$$ و $$E_{\pm} = \frac{\hbar^{2} k^{2}}{2m}$$ در مکانی با پتانسیل صفر، به سمت راست و چپ میرود.
لازم به ذکر است که شدت این امواج به ترتیب $$|A_{+}|^{2}$$ و $$|A_{-}|^{2}$$ نتیجه میشود. توجه داشته باشید از آنجایی که هیچ شرایط مرزی در مسئله وجود ندارد، دو پارامتر عدد موج $$k$$ و انرژی $$E$$ هیچ محدودیتی ندارند.
شاید برایتان راحتتر باشد تا امواج را به صورت سینوسی نشان دهید. با استفاده از رابطه اویلر، میتوان به راحتی فرم نمایی را به فرم سینوسی تبدیل کرد. رابطه اویلر به صورت زیر است:
$$\large e^{i \theta} = \cos \theta + i \sin \theta$$
(13)
$$\large e^{-i \theta} = \cos \theta - i \sin \theta$$
(14)
چگالی احتمال
در بخش قبل بیان کردیم که جمله $$\Psi_{+} (x,t) = A_{+} e^{i (kx - \omega t)}$$ در رابطه (۱۲)، بیانگر موجی است که به سمت راست یا جهت مثبت $$x$$ (یک بعدی) پیش میرود. جمله $$\Psi_{-} (x,t) = A_{-} e^{i (kx + \omega t)}$$ نیز بیانگر موجی است که در جهت منفی $$x$$ پیش میرود. در اینجا میخواهیم چگالی احتمال $$| \Psi |^{ 2 }$$ مربوط به ذره آزادی را که فقط در جهت مثبت محور $$x$$ حرکت میکند، حساب کنیم. در این صورت جمله $$A_{-} e^{i (kx + \omega t)}$$ صفر بوده و رابطه (۱۲) در زمان $$t = 0$$ به صورت زیر در میآید:
$$\large \Psi ( x , t = 0) = \Psi_{+} ( x , t = 0 ) = A_{+} e^{i k x }$$
(15)
جهت محاسبه چگالی احتمال، مجذور قدر مطلق تابع موج $$\Psi_{+} (x,t)$$ را حساب میکنیم. یعنی:
$$\large P_{ + } ( x , t = 0 ) = | \Psi_{+} ( x , t = 0 ) |^{ 2 } = A_{ + } ( e^{ i k x } ) A_{ + } (e^{ i k x })^{ * } = | A_{ + } |^{ 2 }$$
(16)
همانطور که ملاحظه میکنید، چگالی احتمال تابع موج $$\large P_{ + } ( x , t = 0 ) = | \Psi_{+} ( x , t = 0 ) |^{ 2 }$$ به صورت مجذور $$A_{+}$$ یعنی عددی ثابت نتیجه شد. چگالی احتمال ثابت به این معنی است که اگر برای تعیین مکان ذره اندازهگیری انجام دهیم، میبینیم که هر مقداری برای $$x$$ میتواند نتیجه شود (شکل زیر). این امر با اصل عدم قطعیت هماهنگی ندارد.
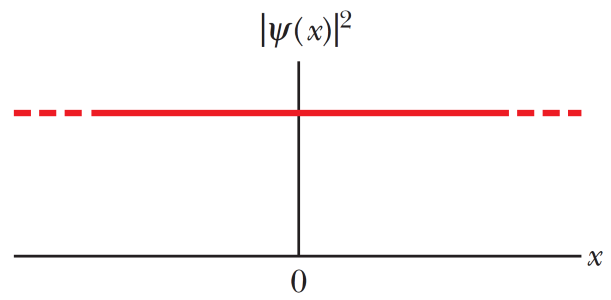
ظرافتهای مسئله ذره آزاد
مسئله ذره آزاد یکی از مسائل مکانیک کوانتومی است که از نقطه نظر محاسبات ریاضی، به سادگی قابل حل است. با این حال مفاهیمی اساسی در این مسئله نهفته است که در ادامه به آنها میپردازیم.
اولین نکتهای که باید به آن توجه کنیم، چگالی احتمال است. همانطور که در بخش قبل دیدیم، چگالی احتمال به صورت ثابت $$| A_{ + } |^{ 2 }$$ نتیجه شد. به عبارت دیگر چگالی احتمال به هیچکدام از متغیرهای مکان $$x$$ و زمان $$t$$ وابسته نیست. این امر منجر به از دست رفتن کامل اطلاعات در خصوص مکان و زمان ذره با مقادیر مشخص تکانه $$p_{ \pm } = \pm \hbar k$$ و انرژی $$E_{ \pm } = \frac{ \hbar^{ 2 } k^{ 2 } }{ 2 m }$$ میشود.
دلیل این امر را میتوان از اصل عدم قطعیت هایزنبرگ فهمید. بر اساس اصل مذکور، تعیین دقیق و همزمان دو پارامتر مکان $$x$$ و تکانه $$P$$ یا زمان $$t$$ و انرژی $$E$$ غیر ممکن است.
$$\large \triangle x \triangle p \geq \frac{\hbar}{2}$$
(17)
$$\large \triangle E \triangle t \geq \frac{\hbar}{2}$$
(18)
از آنجایی که ذره آزاد مذکور دارای تکانه و انرژی مشخص هستند، نتیجه میشود که:
$$\large \triangle p = 0$$
(19)
$$\large \triangle E = 0$$
(20)
در نتیجه طبق اصل عدم قطعیت هایزنبرگ:
$$\large \triangle x\ \rightarrow \infty$$
(21)
$$\large \triangle t\ \rightarrow \infty$$
(22)
نکته دوم مربوط به تفاوت در سرعت ذره با سرعت موجی است که طبق رابطه طول موج دوبروی، باید توصیف کننده ذره مذکور باشد. سرعت موج صفحهای $$\Psi_{\pm} ( x , t )$$ به صورت زیر به دست میآید.
$$\large v_{wave} = f \lambda = \frac{ \omega }{ k } = \frac{ E }{ \hbar k } = \frac{ \hbar^{ 2 } k^{ 2 } / 2 m }{ \hbar k } = \frac{ \hbar k }{ 2 m }$$
(23)
در عبارت فوق، $$v_{wave}$$ سرعت موجی است که طبق رابطه دوبروی، به ذره آزاد اطلاق شده است. از طرفی سرعت ذره کلاسیکی به صورت زیر تعریف میشود:
$$\large v_{classical} = \frac{p}{m} = \frac{\hbar k}{m} = 2 v_{wave}$$
(24)
رابطه فوق بیان میکند که سرعت ذره، دو برابر سرعت موج نماینده ذره یا موج وابسته به ذره است.
نکته سوم مربوط به نرمالایز نبودن تابع موج است. برای آنکه تابع موجی نرمالایز باشد، باید داشته باشیم:
$$\large \int_{ - \infty }^{ + \infty} \Psi_{ \pm }^{ * } \Psi_{ \pm } d x = 1$$
(25)
اما برای تابع موج ذره آزاد داریم:
$$\large \int_{ - \infty }^{ + \infty} \Psi_{ \pm }^{ * } ( x , t ) \Psi_{ \pm } ( x , t ) d x = | A_{ \pm } |^{ 2 } \int_{ - \infty }^{ + \infty} dx \rightarrow \infty$$
(26)
از مطالب فوق بر میآید که تابع موج مذکور $$\Psi_{ \pm } ( x , t ) $$، تابع موج فیزیکی یا واقعی نبوده و ذره آزاد با تکانه و انرژی تعریف شده به صورت دقیق و مشخص نمیتواند وجود داشته باشد. توابع موج فیزیکی، باید انتگرال پذیر مجذوری (square integrable) یا نرمالایز باشند.
سه مشکل اساسی که در بالا مطرح شدند، به دلیل صفحهای در نظر گرفتن موج توصیف کننده ذره پدیدار شدند. به عبارت دیگر، در مسئله ذره آزاد، امواج توصیف کننده موج، به هیچ عنوان نمیتوانند به صورت صفحه (معادله ۸ یا 10) باشند. جهت رفع این مشکل، برهمنهی خطی امواج صفحهای حاصل از حل معادله شرودینگر را در نظر میگیریم. در این صورت بستههای موج (wave packets) به شکل زیر هستند:
$$\large \Psi ( x , t ) = \frac{ 1 }{ \sqrt{ 2 \pi } } \int_{ - \infty }^{ + \infty } \phi ( k ) e^{ i ( k x - \omega t ) } d k$$
(27)
$$\large \phi ( k ) = \frac{ 1 }{ \sqrt{ 2 \pi } } \int_{ - \infty }^{ + \infty } \Psi ( x , t = 0 ) e^{ - i k x } d k$$
(28)
در معادلات فوق، $$\phi ( k )$$ دامنه بسته موج در تبدیل فوریه $$\Psi ( x , t = 0 )$$ است. در صورتی که پاسخ معادله موج شرودینگر برای مسئله ذره آزاد را به صورت بستههای موج در نظر بگیریم، سه مشکل مطرح شده در بالا به راحتی حل میشوند.
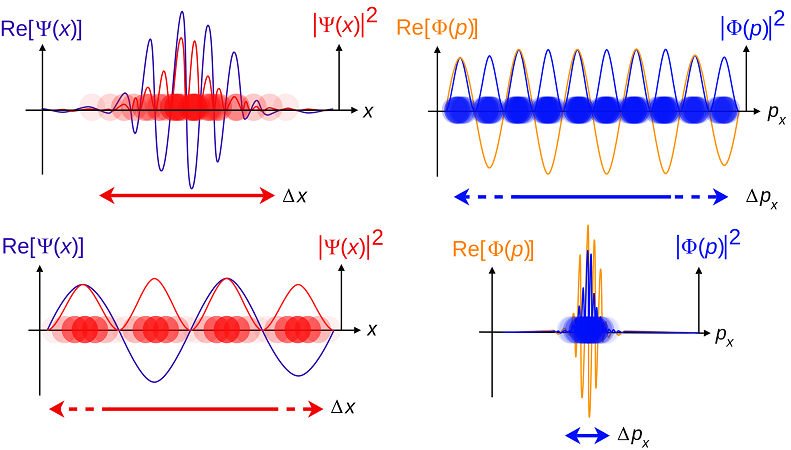
در صورتی که ذره آزاد را توسط یک بسته موج در فضا نشان دهیم، مکان، تکانه و انرژی ذره به صورت دقیق مشخص نبوده و تنها میتوان آنها را به صورت احتمالی بیان کرد. در نتیجه اصل عدم قطعیت پابرجا میماند.
در خصوص مشکل دوم که مربوط به سرعت ذره میشد، با اطلاق بسته موج به ذره، سرعت کلاسیکی $$\frac{ p }{ m }$$ برابر با سرعت گروه (سرعت انتقال بسته موج) میشود. سرعت گروه به صورت زیر تعریف میشود:
$$\large v_{group} = \frac{ \text{d} \omega }{\text{d} k }$$
(29)
با توجه به رابطه (23) داریم:
$$\large v_{wave} = f \lambda = \frac{ \omega }{ k } = \frac{ E }{ \hbar k } = \frac{ \hbar^{ 2 } k^{ 2 } / 2 m }{ \hbar k } = \frac{ \hbar k }{ 2 m } \Rightarrow \omega = \frac{ \hbar k^{2} }{ 2 m }$$
$$\large \Rightarrow v_{group} = \frac{ \text{d} \omega }{\text{d} k } = \frac{ \text{d} }{\text{d} k } ( \frac{ \hbar k^{2} }{ 2 m } ) = \frac{ \hbar k }{ m } \equiv v_{ classical }$$
(30)
بدیهی است که بسته موج معادله (27) نرمالایز بوده و شرط انتگرال پذیر مجذوری نیز محقق میشود.

اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش مروری مکانیک کوانتومی ۲
- مجموعه آموزشهای ریاضی
- آموزش فیزیک مدرن با رویکرد حل مساله
- کامپیوتر کوانتومی -- به زبان ساده
- کیوبیت -- به زبان ساده
- پله پتانسیل -- به زبان ساده
^^










