حرکت دایره ای – به زبان ساده

احتمالا فیلم‌های علمی را مشاهده کرده‌اید. شاید این سوال برایتان پیش آمده باشد که در یک سفینه‌ فضایی، نیروی گرانشی به چه شکل ایجاد می‌شود؟ هم‌چنین فرض کنید که در ماشینی قرار گرفته‌اید که با سرعتی بالا یک پیچ را دور می‌زند. بدیهی است که نیرویی در هنگام دور زدن احساس می‌کنید. آیا می‌دانید منشا این نیرو چیست؟ در این مطلب قصد داریم تا در قالب مفهوم حرکت دایره ای به این سوالات پاسخ دهیم. البته پیشنهاد می‌شود قبل از مطالعه این مطلب، مطالب شتاب، سرعت و بردار را مطالعه فرمایید.

تعریف حرکت دایره‌ ای

حرکت دایره‌ای یکنواخت به حرکتی گفته می‌شود که در آن یک جسم روی مسیری دایره‌ای با سرعتی ثابت در حرکت باشد. برای نمونه پره موتور جتی را در نظر بگیرید که با سرعتی ثابت در حال گردش است؛ یا حرکت چرخ و فلکی را تصور کنید که تعدادی از افراد نیز سوار بر آن هستند. در تمامی این مثال‌ها با حرکت دایره‌ای سروکار داریم.

همان‌طور که پیش‌تر نیز در وبلاگ فرادرس توضیح داده شد، شتاب زمانی وجود دارد که اندازه سرعت جسمی با گذشت زمان تغییر کند. بنابراین در این جا این سوال مطرح است که آیا در حرکت روی مسیر دایره‌ای، شتابی وجود دارد؟

پاسخ سوال فوق مثبت است. دلیل وجود داشتن شتاب، تغییر جهت سرعت با گذشت زمان است. به منظور درک بهتر، در ابتدا شکل زیر را در نظر بگیرید.

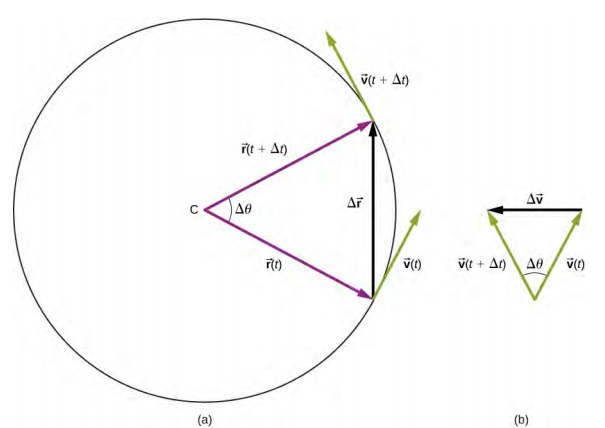
همان‌طور که در شکل فوق نیز می‌بینید، جهت بردار سرعت با گذشت زمان تغییر می‌کند. همین امر کافی است تا جسم، شتابی را روی خودش حس کند. به منظور بدست آوردن شتاب در حرکت دایره‌ای، در ابتدا رابطه مربوط به محاسبه شتاب را به صورت زیر یادآوری می‌کنیم.

$$\large \overrightarrow { a } =\lim _{ { \Delta t } \to 0 } { \frac { \Delta \overrightarrow { v } } { \Delta t } } = { \frac { d \overrightarrow { v } } { d t } }$$
رابطه ۱

در رابطه فوق، المان‌ها به صورت برداری هستند. در بخش بعد از این فرمول استفاده کرده و شتاب را برای حرکت دایره‌ای بدست می‌آوریم.

شتاب مرکزگرا

در سینماتیک یک‌بعدی، اجسامی با سرعت ثابت، شتابی ندارند. اما در حرکت دایره‌ای به دلیل تغییر جهت سرعت با زمان، شتاب نیز وجود دارد. در ابتدا مطابق با شکل ۱ ذره‌ای را در نظر بگیرید که روی مسیری دایره‌ای در حال حرکت است. همان‌طور که می‌بینید سرعت در لحظه t برابر با $$\overrightarrow { v } ( t )$$ و در لحظه $$t + \Delta t$$ معادلِ $$\overrightarrow { V } ( t + \Delta t )$$ در نظر گرفته شده.

فیلم آموزش دینامیک و حرکت دایره ای (رایگان) در فرادرس

کلیک کنید

فرض کنید اندازه سرعت با V و اندازه شعاع با r نمایش داده شود. در این صورت می‌توان تناسب زیر را بین سرعت و شعاع نوشت.

$$\large \frac { \Delta \overrightarrow {v} } { V } = \frac { \Delta \overrightarrow {r} } { r }$$

با استفاده از تناسب فوق، شتاب مرکزگرا به صورت زیر بدست می‌آید.

$$\large a = \lim _ { \Delta t \rightarrow 0 } \left ( \dfrac { \Delta \overrightarrow v } { \Delta t } \right ) = \frac { V } { r } \left ( \lim _ { \Delta t \rightarrow 0 } \dfrac { \Delta \overrightarrow r } {\Delta t } \right ) = \frac {V ^ 2 } { r }$$

جهت بردار شتاب نیز در جهت $${ \Delta \overrightarrow { r } }$$ است. از طرفی این بردار به خود V عمود است. بنابراین بردار شتاب به سمت مرکز دایره است. به همین دلیل به این شتاب مرکزگرا و نیروی ناشی از این شتاب، نیروی مرکزگرا گفته می‌شود. نهایتا شتاب مرکزگرا برابر است با:

$$\large a _ { C } = \frac { v ^ { 2 } } { r }$$

اگر جرم جسم یا ذره در حال حرکت برابر با m باشد، در این صورت نیروی ناشی از شتاب مرکزگرا برابر است با:

$$\large F _ { C } = m \frac { v ^ { 2 } } { r }$$
رابطه ۲

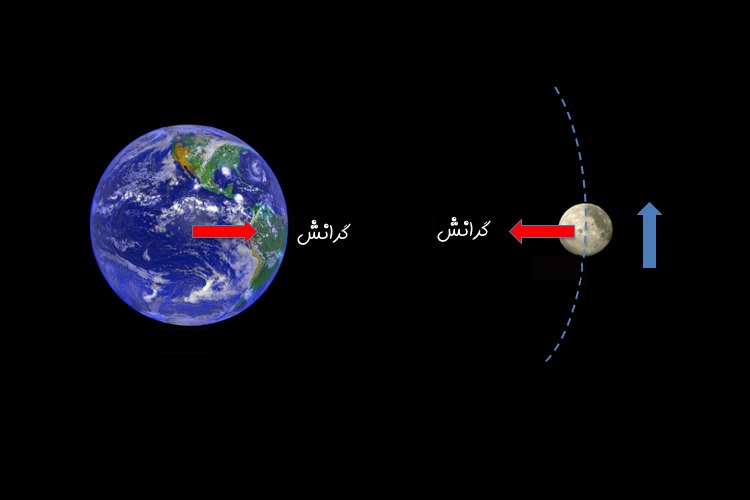
توجه داشته باشید که نیروی گریز از مرکز متفاوت با نیروی مرکزگرا است (البته مقدار آن‌ها در حرکت دایره‌ای یکنواخت برابر است). برای نمونه در هنگام چرخش زمین به دور خورشید نیرویی از جانب خورشید به آن وارد می‌شود که منجر به ثابت ماندن مدار زمین به دور خورشید خواهد شد. یا در حرکت ماه به دور زمین نیز نیرویی مشابه به ماه وارد می‌شود.

حال برمی‌گردیم به سوالی که در مقدمه این مطلب، طرح شد. سوال این بود که در سفینه‌های فضایی به چه شکل نیروی گرانشی ایجاد می‌شود؟ پاسخ در چرخش سفینه است. اگر سفینه با سرعت ثابتی حول محور مشخصی دوران کند، نیرویی به اجزاء درون آن وارد می‌شود که می‌تواند افراد و اجزا درون آن را به سطح سفینه بچسباند.

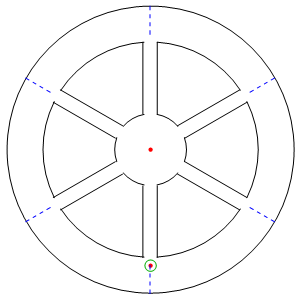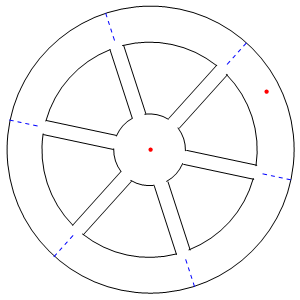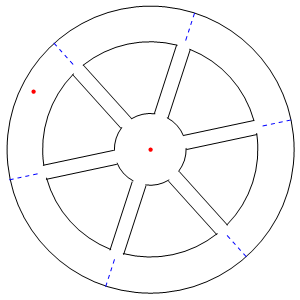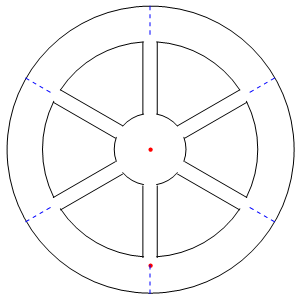
در انیمیشن زیر نیز مکانیزم تولید گرانش مصنوعی در سفینه فوق نشان داده شده است. همان‌طور که می‌بینید نقطه قرمز رنگ نیرویی را روی خودش احساس می‌کند که باعث می‌شود در صورت جدا شدن از سطح، دوباره به سمت آن بازگردد.

مثال ۱

هواپیمای جتی را در نظر بگیرید که با سرعت $$1 3 4 . 1 \ m / s$$ در حال حرکت است. به منظور ایجاد شتاب g یا همان $$9 . 8 \ m / s ^ 2$$ این جت دایره‌ای با کدام شعاع را باید طی کند؟

با برابر قرار دادن شتاب g با رابطه ۲ داریم:

$$\large a _ C = g = 9 . 8 = \frac { V ^ 2 } { r } \Rightarrow \ \ r = \frac { V ^ 2 } { g }$$

با جایگذاری مقادیر در عبارت بدست آمده در بالا داریم:

$$\large r = \frac { (1 3 4 . 1 \ m / s)^2 } { 9 . 8 \ m / s ^ 2 } = 1835 \ m = 1 . 8 3 5 k m$$

بدیهی است که به منظور افزایش شتاب، یا شعاع منحنی باید کاهش یافته و یا سرعت جت باید افزایش یابد.

معادله حرکت دایره‌ای یکنواخت

حرکت دایره‌ای یک ذره را می‌توان با استفاده از تابعی برداری تعیین کرد. به منظور توضیح تابع توصیف کننده حرکت ذره، در ابتدا فرض کنید که ذره روی مسیری به شکل زیر در حرکت است.

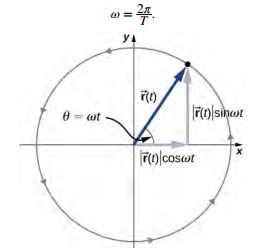
با توجه به شکل فوق، تابع توصیف کننده موقعیت ذره را به صورت زیر نشان می‌دهند.

$$\large \overrightarrow { r } ( t ) = A \cos \omega t \widehat { i } + A \sin \omega t \widehat { j }$$

$$\omega$$ برابر با سرعت زاویه‌ای یا همان فرکانس زاویه‌ای است. واحد این کمیت نیز ثانیه/رادیان ($$\frac { r a d } { s }$$) در نظر گرفته می‌شود. زاویه‌ای که ذره در هر لحظه با محور xها دارد، θ است که معادل با $$\theta = \omega t$$ محاسبه می‌شود.

با توجه به رابطه $$\theta = \omega t$$، می‌توان زمانِ یک دور زدنِ ذره را به صورت زیر محاسبه کرد.

$$\large \theta = \omega t \Rightarrow 2 \pi = \omega t \Rightarrow T = \frac { 2 \pi } { \omega }$$

زمان T یا زمانی که طول می‌کشد تا ذره یک دور کامل بزند را دوره می‌گویند. البته می‌توان با استفاده از مشتق‌گیری از تابع $$\overrightarrow { r } ( t )$$ نیز سرعت و شتاب ذره را بدست آورد. برای نمونه رابطه برداری سرعت برابر است با:

$$\large \overrightarrow { v } ( t ) = \frac { d \overrightarrow { r } ( t ) } { d t } = - A \omega \sin \omega t \hat { i } + A \omega \cos \omega t \hat { j }$$

هم‌چنین با مشتق‌گیری از رابطه بالا، مقدار شتاب در هر لحظه نیز به صورت زیر محاسبه می‌شود.

$$\large \overrightarrow { a } ( t ) = \frac { d \overrightarrow { v } ( t ) } { d t } = - A \omega ^ { 2 } \cos \omega t \hat { i } - A \omega ^ { 2 } \sin \omega t \hat { j }$$

با توجه به سرعت و شتاب بدست آمده در بالا،‌ می‌توان دید که سرعت به مسیر دایره‌ایی مماس و شتاب نیز به مسیر عمود است.

مثال ۲

یک پروتون با سرعت $$5 × 1 0 ^ { 6 } \ m / s$$ مسیری دایره‌ای به شعاع $$r = 0 . 1 7 5 \ m$$ را طی می‌کند. در زمان t=0 موقعیت بردار پروتون برابر با $$r = 0 . 1 7 5 \ m \ \widehat { i }$$ است. با این فرض موقعیت پروتون را در لحظه $$t = 2 . 0 × 1 0 ^ { - 7 } s = 2 0 0 \ n s$$ بدست آورید. همچنین موقعیت ذره را در لحظه مذکور ترسیم کنید.

با توجه به اطلاعات بیان شده، دوره تناوب و فرکانس زاویه‌ای حرکت ذره برابرند با:

$$\large T = \frac { 2 \pi r } { v } = \frac { 2 \pi ( 0 . 1 7 5 \; m ) } { 5 . 0 \times 1 0 ^ { 6 } \; m / s } = 2 . 2 0 \times 1 0 ^ { - 7 } \; s$$

$$\large \omega = \frac { 2 \pi } { T } = 2.857 × 10 ^ {7}$$

در نتیجه موقعیت ذره در زمان $$t = 2 . 0 × 1 0 ^ { - 7 } s = 2 0 0 \ n s$$ برابر است با:

$$\large \begin {align*} \overrightarrow { r } ( 2 . 0 \times 1 0 ^ { - 7 } \; s) & = A \cos \omega ( 2 . 0 \times 1 0 ^ { - 7 } \; s ) \widehat { i } + A \sin \omega ( 2 . 0 \times 1 0 ^ { - 7 } \; s) \hat { j } \; m \\ & = 0 . 1 7 5 \cos ( 5 . 7 1 2 \; rad ) \hat { i } + 0 . 1 7 5 \sin ( 5 . 1 7 2 \; rad ) \widehat { j } \; m \\ & = 0 . 1 4 7 \widehat { i } - 0 . 0 9 5 \widehat{ j } \; m \ldotp \end{align*}$$

هم‌چنین با توجه به بردار بدست آمده در بالا،‌ موقعیت ذره در این لحظه به صورت زیر است.

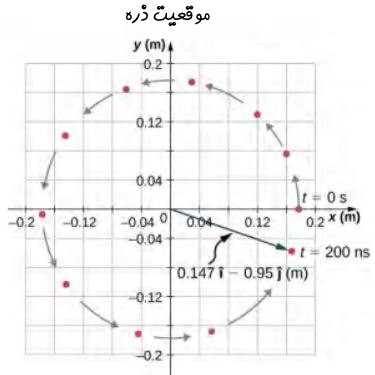
حرکت دایره‌ای غیر یکنواخت

حرکت دایره‌ای غیر یکنواخت حرکتی با مسیر دایره‌ای است که در آن سرعت مماس و زاویه‌ای به طور ثابت کاهش یا افزایش می‌یابند (این تغییر بستگی به جهت هر کدام از شتاب‌ها دارد). در حرکت دایره‌ای غیر یکنواخت سه نوع شتاب به نام‌های شتاب های زاویه‌ای، مماسی، و مرکزگرا وجود دارند.

همان‌گونه که گفته شد در حرکت دایره‌ای غیریکنواخت سرعت‌ها و شتا‌ب‌های متعددی وجود دارند. از این‌رو، آشنایی با مفاهیم سرعت و شتاب بسیار ضروری است. به طور مثال، وقتی گفته می‌شود که شتاب جسمی $$1\frac{m}{s^2}$$ است بدین معنی است که سرعت آن جسم در هر ثانیه $$1\frac{m}{s}$$ سریع‌تر خواهد بود.

در حرکت دایره‌ای غیریکنواخت توجه به دو نکته زیر بسیار حائز اهمیت است:

1. شعاع دایره می‌تواند ثابت باشد (مانند حرکت در امتداد ریل دایره‌ای). تغییر در سرعت می‌تواند بزرگی شتاب شعاعی را تغییر دهد. این تغییر بدان معنا است که شتاب مرکزگرا مانند ثابت نیست و هرچه سرعت بزرگ‌تر باشد شتاب شعاعی نیز بزرگ‌تر است. در حالتی که شعاع دایره ثابت است، ذره‌ای که با سرعت بیشتری حرکت می‌کند نیاز به نیروی شعاعی بزرگ‌تری به منظور تغییر جهت خواهد داشت.
2. وقتی نیروی شعاعی یا مرکزگرا ثابت باشد (مانند حرکت سفینه فضایی به دور زمین تحت تاثیر نیروی ثابت گرانش)، حرکت دایره‌ای شعاعش را در واسخ به تغییر سرعت تنظیم می‌کند. این بدان معناست که برخلاف حرکت دایره‌ای یکنواخت، شعاع مسیر دایره‌ای متغیر خواهد بود. ذکر این نکته مهم است که تغییر در سرعت ذره گرچه بر شتاب شعاعی تاثیر می‌گذارد ولی این تغییر متاثر از نیروی مرکزگرا نخواهد بود. برای تغییر مقدار سرعت مماسی نیاز به نیروی مماسی است.

سرعت و شتاب در حرکت دایره‌ای غیر یکنواخت

همان‌طور که می‌دانیم حرکت دایره‌ای در حالت کلی به دو قسمت زاویه‌ای و مماسی تقسیم ‌می‌شود. قسمت زاویه‌ای مانند سرعت چرخش و شتاب زاویه‌ای مربوط به چرخش جسم است. به هنگام حل مساله در این قسمت، اندازه‌های طولی اهمیتی نداشته و قسمت مورد توجه تنها مقادیر زاویه‌ای است. قسمت مماسی حرکت دایره‌ای هر چیزی را که مربوط به طول است شامل می‌شود.

به منظور فرمول‌‌بندی حرکت دایره‌ای غیر یکنواخت نیاز به دانستن اطلاعات زیر است.

• شتاب زاویه‌ای ($$\alpha$$): به افزایش یا کاهش سرعت زاویه‌ای شتاب زاویه‌ای گفته می‌شود که اندازه‌اش ثابت و واحد آن $$\frac{rad}{s^2}$$ است.
• سرعت زاویه ای ($$\omega$$): در مباحث بالاتر توضیح داده شده است.
• شتاب مماسی ($$a_{t}$$): همان نوع شتابی است که در حرکات بر روی خط مستقیم استفاده می‌شود و واحد آن $$\frac{m}{s^2}$$ است.
• سرعت مماسی ( $$v_{t}$$): سرعت مماسی در حرکت دایره‌ای غیر یکنواخت مانند سرعت زاویه‌ای هموراه دارای مقادیر اولیه و نهایی است.
• شتاب مرکزگرا ($$a_{c}$$): در مباحث بالاتر توضیح داده شده است.
• S: برابر فاصله‌ای است شی طی می‌کند.

فرمول‌های حرکت دایره‌ای غیر یکنواخت

در ادامه به فرمو‌ل‌های حرکت دایره‌ای غیر یکنواخت پرداخته می‌شود. در ابتدا فرمول‌های مربوط به قسمت مماسی حرکت بیان می‌شود.

$$a_{t}=\frac{V_{f}-V_{0}}{t}$$

$$S=V_{0}t+\frac{1}{2}a_{t}t^{2}$$

$$V_f^2= V_0^2 + 2a_{t}S$$

$$S= \frac{V_{0} + V_{f}}{2}t$$

در ادامه فرمول‌های قسمت زاویه‌ای گفته می‌شود.

$$\alpha = \frac{\omega_{f} - \omega_{0}}{2} t$$

$$\theta = \omega_{0} t+\frac{1}{2}\alpha t^{2}$$

$$\omega_f^2 = \omega^0_{2}+ 2\alpha \theta$$

$$\theta = \frac{\omega_{0}+ \omega_{f}}{2} t$$

در حرکت دایره‌ای غیر یکنواخت می‌توان از طریق روابط زیر قسمت زاویه‌ای را به قسمت مماسی ربط داد.

$$\omega_{f} = \frac{V_{f}}{R}$$

$$\omega_{0}= \frac{V_{0}}{R}$$

$$\alpha= \frac{a_{t}}{R}$$

$$\theta= \frac{S}{R}$$

مثال 3

مورچه‌ای بر روی میز چرخانی قرار دارد. میز با سرعت زاویه‌ای $$\alpha= 1 \frac{rad}{s^{2}}$$ از حالت سکون شروع به چرخش می‌کند. مورچه در فاصله $$R= 0.1 m$$ از مرکز میز قرار دارد.  اگر ضریب اصطکاک ایستایی بین مورچه و میز 0/5 باشد، پس از چه مدت زمانی مورچه بر اثر چرخش میز از جای خود حرکت ‌می‌کند؟

وقتی میز چرخان شتاب می‌گیرد، نیروی اصطکاک ایستایی بین میز و مورچه موجب حرکت مورچه با میز می‌شود. نیروهای وارد به مورچه به صورت زیر هستند.

• نیروی وزن مورچه، $$\overrightarrow{F_{g}}$$، با بزرگی mg
• نیروی عمود بر سطح، $$\overrightarrow{N}$$، که از طرف میز چرخان بر مورچه وارد می‌شود.
• نیروی اصطکاک ایستایی، $$\overrightarrow{f_{s}}$$، که از طرف میز بر مورچه وارد می‌شود. نیروی اصطکاک دارای دو مولفه شعاعی و مماسی است.

نمودار نیروهای وارد بر مورچه از دیدگاه بالا و جانبی در شکل نشان داده شده است. این نیروها برای زمانی رسم شده است که بعد از این زمان مورچه از روی میز به کنار حرکت می‌کند. در این هنگام نیروی اصطکاک با محور x زاویه نامشخص $$\theta$$ را ساخته است. در این مساله دستگاه مختصات سه‌بعدی استفاده شده است به گونه‌ای که مرکز میز به عنوان مبدا محور مختصات در نظر گرفته شده و مورچه در جهت مثبت محور x قرار گرفته است. سرعت مورچه در جهت مثبت محور y است. همچنین، نیروهای وزن و عمود بر سطح از طرف میز در جهت محور z قرار گرفته‌اند. بردار شتاب مورچه نیز دارای دو مولفه شعاعی (جهت محور x) و مماسی (جهت محور y) خواهد بود.

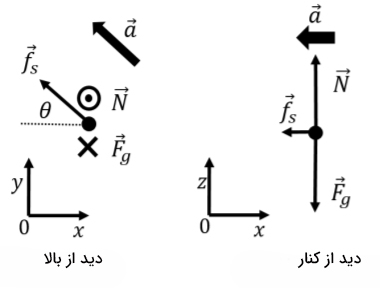
قانون سوم نیوتن را در سه راستای xyz به صورت زیر می‌نویسیم.

در راستای z نیروهای وزن و نیروی عمود بر سطح را داریم:

چون N = mg، بنابراین خواهیم داشت:

$$\sum F_{z}= N - F_{g}= 0$$

فیلم آموزش فیزیک پایه ۱ – مرور و حل تست در فرادرس

کلیک کنید

در راستای x، مولفه شعاعی شتاب را داریم.

$$\sum F_{x}= -f_{s}cos(\theta)= -ma_{R} = -m\frac{v^{2}}{R}$$

در راستای y، مولفه مماسی شتاب را داریم.

$$\sum F_{y}= f_{s}sin(\theta)= ma_{T}$$

که

$$f_{s}sin(\theta)= m\alpha R$$

در رابطه بالا از فرمول

$$a_{T}=\alpha R$$

با در نظر گرفتن معادلات نوشته شده برای نیروها در سه جهت محور مختصات به روابط زیر می‌رسیم

$$f_{s}cos(\theta) = m\frac{v^{2}}{R}$$

$$f_{s}sin(\theta) = m\alpha R$$

$$N=mg$$

همچنین سرعت در زمان ‌t، به این صورت نوشته می‌شود.

$$v(t)=v_{0}+a_{T}t = (0) + \alpha Rt$$

زمانی که نیروی اصطکاک به حداکثر دامنه خود می‌رسد مورچه شروع به لغزیدن می‌کند‌، $$f_{s}=\mu_{s}N=\mu_{s}mg$$. با استفاده از مولفه نیرو در راستای x، رابطه زیر برای زمانی که مورچه شروع به لغزیدن از روی میز می‌کند به دست می‌آید.

$$f_{s}cos(\theta) = m\frac{v^{2}}{R}$$

$$\mu_{s}gcos(\theta)=R \alpha^{2}t^{2}$$

$$t=\sqrt{\frac{\mu_{s}gcos(\theta)}{R \alpha^{2}}}$$

چون مقدار زاویه مشخص نیست، برای به دست آوردن آن میتوان از مولفه y نیرو استفاده کرد.

$$f_{s}sin(\theta)=m \alpha R$$

$$\mu_{s}gsin(\theta)= \alpha R$$

$$sin(\theta)=\frac{\alpha R}{\mu_{s}g}=sin^{-1}(\frac{(1 rad/s^{2}(0.1 m)}{(0.5)(9.8N/kg)}) = 1.17$$

با جایگزینی زاویه به دست آمده در رابطه به دست آمده برای زمان، مقدار آن حدود 7 ثانیه به دست می‌‌آید.

مثال 4

ذره‌ای روی مسیری دایره‌ای به شعاع r=2 در بازه زمانی t = 1.5 s تا t = 4.0 s در حال حرکت است. فرض کنید در بازه مذکور، سرعت خطی این ذره مطابق با رابطه زیر تغییر کند.

$$\large v ( t ) = c _ { 1 } - \frac { c _ { 2 } } { t ^ { 2 } } , c _ { 1 } = 4 . 0 \; m / s , c _ { 2 } = 6 . 0 \; \ \ m \cdotp s$$

شتاب کلی ذره را در لحظه t=2s بیابید.

به منظور یافتن پاسخ در ابتدا باید سرعت را در لحظه t=2s بیابیم. سرعت در این لحظه برابر است با:

$$\large v( 2 . 0 \; s ) = \left (4 . 0 - \dfrac { 6 . 0 } { ( 2 . 0 ) ^ { 2 } } \right ) m / s = 2 . 5 \; m / s$$

با بدست آمدن سرعت خطی، شتاب مرکزگرا نیز به صورت زیر بدست می‌آید.

$$\large a _ { C } = \frac { v ^ { 2 } } { r } = \frac { ( 2 . 5 \; m / s ) ^ { 2 } } { 2 . 0 \; m } = 3 . 1 \; m / s ^ { 2 }$$

از طرفی شتاب مماسی برابر است با:

$$\large a _ { T } = \Big | \frac { d \overrightarrow{ v } } { d t } \Big | = \frac { 2 c _ { 2 } } { t ^ { 3 } } = \frac { 1 2 . 0 } { ( 2 . 0 ) ^ { 3 } } m / s ^ { 2 } = 1 . 5 \; m / s ^ { 2 }$$

حال کافی است تا دو شتاب را همان‌طور که در ادامه محاسبه شده، به صورت برداری با یکدیگر جمع کنیم.

$$\large | \overrightarrow { a } | = \sqrt { 3 . 1 ^ { 2 } + 1 . 5 ^ { 2 } } m / s ^ { 2 } = 3 . 4 4 \; m / s ^ { 2 }$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های ریاضی و فیزیک
• قضیه کار و انرژی -- به زبان ساده
• اصطکاک — به زبان ساده