توزیع لجستیک و متغیر تصادفی آن — به زبان ساده

در نظریه آمار و احتمال، توزیع لجستیک (Logistic Distribution) و متغیر تصادفی آن (Logistic Distribution Random Variable) از اهمیت زیادی برخوردار هستند. بخصوص در مبحث مربوط به رگرسیون لجستیک، از این توزیع و متغیر تصادفی آن بسیار استفاده می‌شود. متغیر تصادفی لجستیک، دارای یک توزیع پیوسته بوده و تابع توزیع احتمال تجمعی (Cumulative Distribution Function) آن یک تابع لجستیک (Logistic Function) است. جالب است که بدانید رگرسیون لجستیک در شبکه عصبی و دسته‌بندی (Classification) نیز به کار گرفته می‌شود.

از آنجایی که در این نوشتار از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد، بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین اگر به رگرسیون لجستیک و خصوصیات آن علاقه‌مند باشید، می‌توانید مطلب رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS را بخوانید.

توزیع لجستیک و متغیر تصادفی آن

توزیع متغیر تصادفی لجستیک، شبیه توزیع نرمال است ولی در دم‌ها، میزان احتمال بیشتر از توزیع نرمال است. بنابراین می‌توان توزیع لجستیک را در گروه توزیع‌های دم-سنگین در نظر گرفت. توزیع لجستیک نوع خاصی از «توزیع لاندا توکی» (Tukey Lambda Distribution) است.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

به عنوان یک تعریف رسمی می‌توان گفت که متغیر تصادفی $$X$$ دارای توزیع لجستیک است اگر تابع چگالی احتمال (Probability Density Function) آن به صورت زیر نوشته شود.

$$\large {\displaystyle {\begin{aligned}f(x;\mu ,s)&={\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\\[4pt]&={\frac {1}{s\left(e^{(x-\mu )/(2s)}+e^{-(x-\mu )/(2s)}\right)^{2}}}\\[4pt]&={\frac {1}{4s}}\operatorname {sech} ^{2}\left({\frac {x-\mu }{2s}}\right)\end{aligned}}}$$

پارامترهای این توزیع $$\mu$$ یا پارامتر مکان (Location) و $$s$$ نیز پارامتر مقیاس (Scale) بوده و تابع چگالی حول میانگین متقارن است. در نتیجه می‌توان گفت که میانگین (Mean)، میانه (Median) و نما (Mode) برای این متغیر تصادفی همگی با $$\mu$$ برابر خواهد بود. تکیه‌گاه متغیر تصادفی لجستیک، مجموعه اعداد حقیقی است. بنابراین اگر متغیر تصادفی $$X$$ دارای توزیع لجستیک باشد، می‌نویسیم،

$$\large X \sim \mathrm{Logistic}(\mu , s)$$

‌و می‌خوانیم $$X$$ دارای توزیع لجستیک با پارامترهای مکان $$\mu$$ و مقیاس $$s$$ است.

از آنجایی که این تابع چگالی برحسب تابع «سکانت هایپربولیک» (Sech) است، گاهی به آن توزیع سکانت هایپربولیک (Hyperbolic Secant Distribution) نیز می‌گویند.

نکته: زمانی که میانگین توزیع صفر بوده ($$\mu=0$$) و پارامتر مقیاس نیز برابر با ۱ باشد ($$s=1$$)، آنگاه توزیع لجستیک را استاندارد می‌نامیم و می‌نویسیم.

$$\large {\displaystyle {\begin{aligned}f(x;0,1)&={\frac {e^{-x}}{(1+e^{-x})^{2}}}\\[4pt]&={\frac {1}{(e^{x/2}+e^{-x/2})^{2}}}\\[5pt]&={\frac {1}{4}}\operatorname {sech} ^{2}\left({\frac {x}{2}}\right).\end{aligned}}}$$

در تصویر ۱ نمودارهای چگالی احتمال متغیر تصادفی لجستیک با پارامترهای مختلف مرکزی و مقیاس نمایش داده شده است.

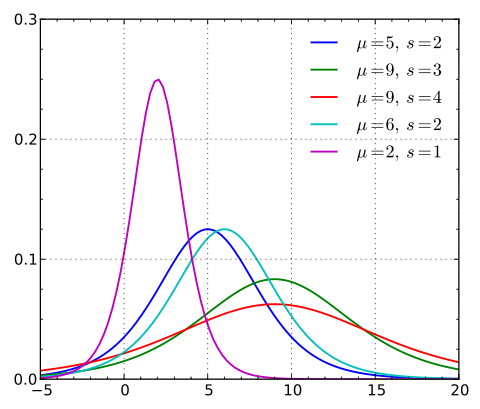
تابع توزیع تجمعی احتمال متغیر تصادفی لجستیک

توزیع لجستیک نام خود را از توزیع تجمعی (انباشته) گرفته است، که نمونه‌ای از خانواده توابع لجستیک است. به این ترتیب تابع توزیع تجمعی متغیر تصادفی $$X$$ به صورت زیر نوشته خواهد شد.

$$\large{\displaystyle F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}={\frac {1}{2}}+{\frac {1}{2}}\operatorname {tanh} \left({\frac {x-\mu }{2s}}\right)}$$

در تصویر ۲ نیز نمودار تابع توزیع تجمعی احتمال برای متغیر تصادفی لجستیک با پارامترهای مختلف ترسیم شده است. همانطور که انتظار داریم، شکل این منحنی‌ها به صورت $$S$$ بوده و کمترین مقدار برابر با صفر و بیشترین مقدار این تابع برابر با ۱ است. شیب این تغییرات وابسته با پارامتر مقیاس است به طوری که برای مقدار $$s=4$$، شیب تغییرات کم بوده و به ازاء $$s=1$$ شیب تغییرات، بیشتر است.

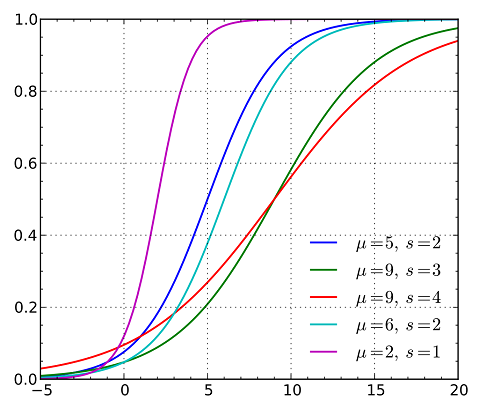
ارتباط با توزیع‌های دیگر

توزیع متغیر تصادفی لجستیک با دیگر توزیع‌های آماری در ارتباط است. در ادامه به بعضی از این توزیع‌ها اشاره خواهیم کرد.

• اگر $$X\sim \operatorname{Logistic} (\mu , s)$$ آنگاه $$kX+l\sim \operatorname{Logistic} (k\mu+l,ks)$$
• اگر $$X\sim \mathrm{U}(0,1)$$ آنگاه $$\mu+s(\log(X)-\log(1-X)) \sim \operatorname{Logistic} (\mu,s)$$.
• اگر $$X\sim \mathrm{Gumbel}(\alpha X,s)$$ و $$Y\sim \mathrm{Gumbel}(\alpha Y,s)$$ آنگاه $${\displaystyle X-Y\sim \mathrm {Logistic} (\alpha _{X}-\alpha _{Y},\beta )\,}$$.
• برای دو متغیر $$X \text{ و } {\displaystyle Y\sim \mathrm {Gumbel} (\alpha ,\beta )}$$، داریم $${\displaystyle X+Y\nsim \mathrm {Logistic} (2\alpha ,\beta )}$$ به این معنی که مجموعه دو توزیع گامبل، دارای توزیع لجستیک نیست هر چند که تفاضل‌ آن‌ها دارای توزیع لجستیک است.
• امید ریاضی در توزیع لجستیک خاصیت جمعی ندارد به این معنی که

$$\large {\displaystyle \operatorname{E}(X+Y)=2\alpha +2\beta \gamma \neq 2\alpha =\operatorname{E}\left(\mathrm {Logistic} (2\alpha ,\beta )\right)}$$

• اگر $$X\sim \mathrm{Logistic}(\mu,s)$$ آنگاه تابع نمایی از $$X$$ دارای توزیع لگ‌لجستیک خواهد بود.

$$\large \exp(X) \sim \operatorname{LogLogistic}{\displaystyle \left(\alpha =e^{\mu },\beta ={\frac {1}{s}}\right)}$$

• اگر $$X\sim \mathrm{Exp}(1)$$ (توزیع نمایی) باشد، آنگاه

$$\large {\displaystyle \mu +\beta \log(e^{X}-1)\sim \operatorname {Logistic} (\mu ,\beta ).}$$

• همچنین اگر $$X$$ و $$Y$$ دارای توزیع نمایی با پارامتر ۱ باشند، آنگاه

$$\large {\displaystyle \mu -\beta \log \left({\frac {X}{Y}}\right)\sim \operatorname {Logistic} (\mu ,\beta ).}$$

کاربرد توزیع لجستیک

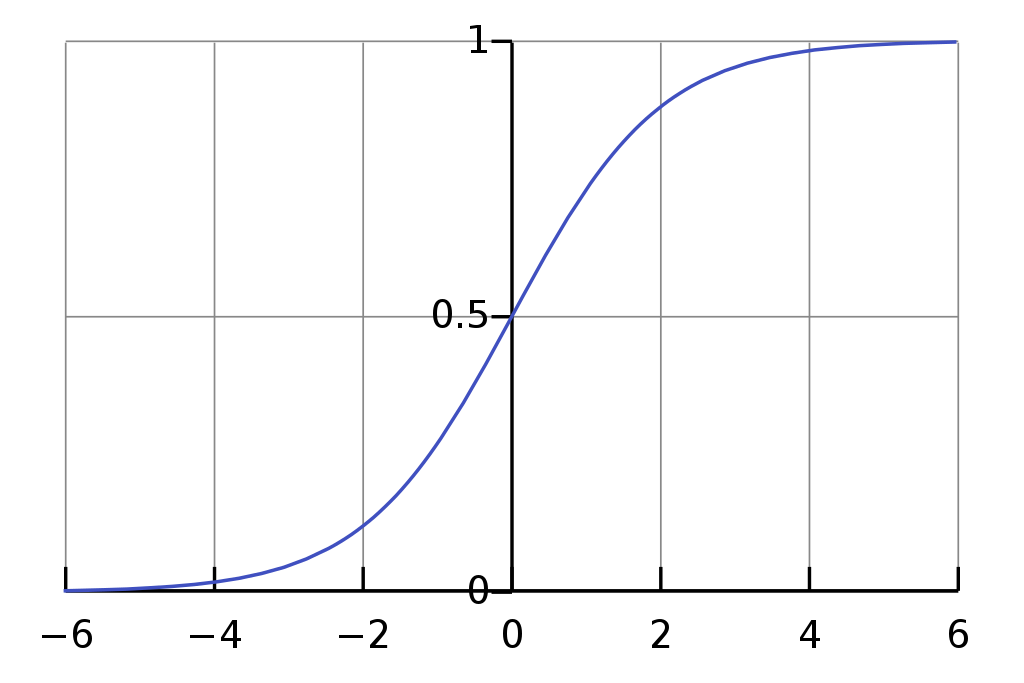
از نکات مهم و کاربردی برای توزیع و متغیر تصادفی لجستیک می‌توان به ارتباط آن با تابع لجستیک (Logistic Function) اشاره کرد. تابع $$s$$ شکل به فرم زیر را تابع لجستیک یا منحنی سیگموئید (Sigmoid Curve) می‌نامیم.

$$\large {\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}}}$$

که در آن $$x_0$$ نقطه مرکزی نمودار سیگموئید و $$L$$ نیز حداکثر این تابع را مشخص می‌کند. پارامتر $$k$$ نیز نرخ تغییرات در بین حداکثر و حداقل این تابع را تعیین می‌کند.

همچنین در بحث یادگیری عمیق (Deep Learning) تابع لوجیت (Logit Function) نیز که به مانند تابع لجستیک حالت $$s$$ شکل دارد، به کار گرفته می‌شود. اگر $$p$$ نشان دهنده تابع احتمال باشد، آنگاه رابطه زیر را تابع لوجیت می‌نامند.

$$\large {\displaystyle \operatorname {logit} (p)=\log \left({\frac {p}{1-p}}\right)=\log(p)-\log(1-p)=-\log \left({\frac {1}{p}}-1\right)}$$

رگرسیون لجستیک (Logistic Regression)

یکی از رایج ترین کاربردهای توزیع لجستیک و متغیر تصادفی آن، رگرسیون لجستیک است که برای مدل‌سازی متغیرهای وابسته از نوع طبقه‌ای (مثلاً گزینه‌های بله-خیر ) مورد استفاده قرار می‌گیرد. این امر درست به مانند حالتی است که از رگرسیون خطی ساده برای مدل‌سازی متغیرهای وابسته از نوع پیوسته کمک گرفته می‌شود.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

به طور خاص، رگرسیون لجستیک می‌تواند به عنوان مدل‌هایی براساس «متغیر پنهان» (Latent Variable) و «متغیرهای خطا» (Error Variables) با توزیع لجستیک، بیان شود. به این ترتیب توزیع لجستیک همان نقشی را در رگرسیون لجستیک خواهد داشت که در رگرسیون باینری (Probit Regression)، توزیع نرمال (Normal Distribution) ایفا می‌کند.

از آنجایی که توزیع لجستیک دارای دم‌های سنگین‌تری نسبت به توزیع نرمال است، اغلب، تحلیل‌ها و برآوردهای استوارتری (Robust) نسبت به تحلیل‌های با توزیع نرمال ایجاد می‌کند.

کاربرد در فیزیک

تابع چگالی احتمال متغیر تصادفی لجستیک (PDF) دارای فرم عملکردی مشابه با مشتق تابع فِرمی (Fermi Function) است. مشتق این تابع در نظریه خواص الکترون در نیمه هادی‌ها و فلزات، وزن‌های متفاوتی را برای انرژی الکترون‌های مختلف محاسبه می‌کند. توجه داشته باشید که توزیع احتمال مربوط به این پدیده شبیه توزیع لجستیک است.

توزیع لجستیک را می‌توان به عنوان توزیع حدی سرعت نهایی حرکت تصادفی میرای یک ذره در فرآیند برنولی در نظر گرفت که در آن تغییرات سرعت در زمان‌های تصادفی رخ داده و دارای توزیع نمایی با پارامترهای صعودی خطی است.

کاربرد در علوم آب

در هیدرولوژی و علوم آب، توزیع تخلیه رودخانه و بارندگی در طولانی مدت (به عنوان مثال، در مقاطع ماهانه و سالانه) غالباً طبق قضیه حد مرکزی (Central Limit Theorem) به طور مجانبی دارای توزیع نرمال است.

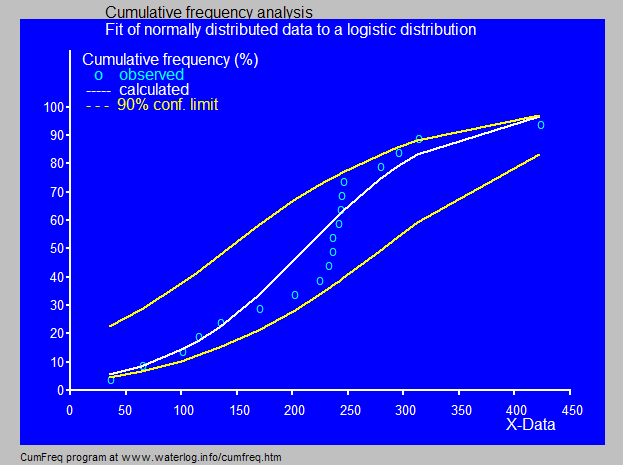
از آنجای که توزیع لجستیک، مشابه توزیع نرمال، دارای روش‌های تحلیلی است، در بسیاری از موارد می‌تواند جایگزین توزیع نرمال شود. در تصویر ۴، از توزیع لجستیک برای برآورد کردن میزان بارندگی در ماه اکتبر، استفاده شده و نمونه تصادفی جمع‌آوری شده به خوبی با توزیع لجستیک با یک فاصله اطمینان ۹۰ درصدی، همخوانی دارد.

خلاصه و جمع‌بندی

در این نوشتار با تابع توزیع لجستیک و متغیر تصادفی آن آشنا شدیم و خصوصیات آن را مورد بررسی قرار دادیم. از طرفی ارتباط این متغیر تصادفی را با توزیع‌های دیگر مشخص کردیم. همچنین کاربردهای مختلف این توزیع را در علوم دیگر متذکر شدیم. از آنجایی که این توزیع نسبت به توزیع نرمال دارای دم‌های سنگین‌تری در چگالی احتمال است، در مواردی که با داده‌ها دم-سنگین (Heavy Tail Data) مواجه هستیم، استفاده از این توزیع و مدل‌سازی برمبنای آن باعث افزایش دقت در برآوردها خواهد شد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های SPSS
• آموزش یادگیری عمیق (Deep learning)
• مجموعه آموزش‌های آمار و احتمال
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^