تناسب در ریاضی چیست؟ – به زبان ساده + سوال با جواب

در آموزش‌های پیشین مجله فرادرس، با نسبت در ریاضی آشنا شدیم. در این آموزش، با تناسب در ریاضی آشنا می‌شویم و مثال‌هایی از آن را حل خواهیم کرد.

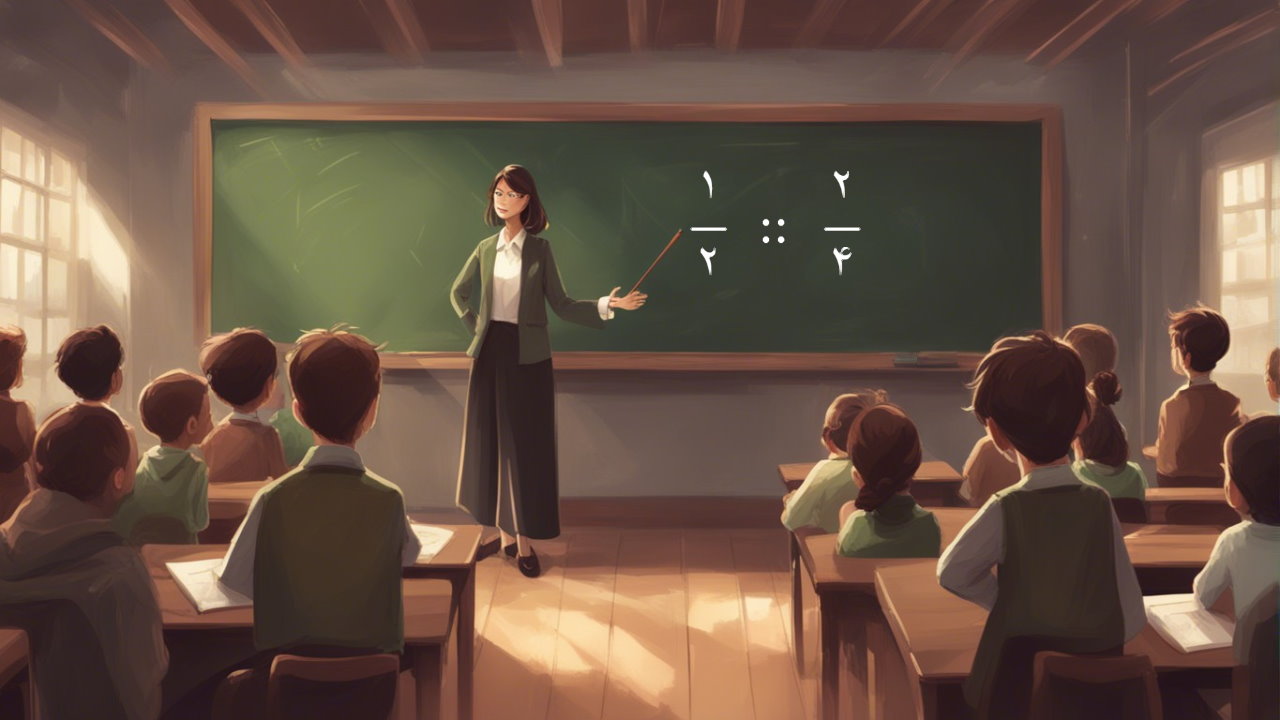
تناسب در ریاضی چیست؟

تناسب در ریاضی عمدتاً بر اساس نسبت یا همان کسر توضیح داده می‌شود. در آموزش‌های پیشین دیدیم که نسبت دو کمیت $$a$$ و $$b$$ را می‌توان به شکل کسری $$\frac a b$$ نمایش داد.

برای مثال، اگر در یک کلاس ۵۰ نفری، ۲۷ دانش‌آموز دختر و بقیه پسر باشند، نسبت تعداد دانش‌آموزان دختر به کل دانش‌آموزان این کلاس ۲۷ به ۵۰ یا به‌صورت کسری $$\frac {27}{50}$$ است. اگر صورت و مخرج این کسر را در یک عدد ضرب کنیم، نسبت تغییری نمی‌کند. مثلاً اگر صورت و مخرج را در ۲ ضرب کنیم، به نسبت $$\frac {54}{100}$$ می‌رسیم که مساوی با نسبت $$\frac {27}{50}$$ است. این دو نسبت مساوی یک تناسب را تشکیل می‌دهند.

بدین ترتیب، «تناسب» (Proportion) رابطه بین دو نسبت را بیان می‌کند و این رابطه از نوع تساوی است. یعنی اگر دو نسبت با هم برابر باشند، می‌گوییم تناسب دارند یا متناسب هستند. بنابراین، نسبت رابطه‌ای بین دو عدد است و تناسب رابطه‌ای بین دو نسبت. نسبت و تناسب مفاهیمی کلیدی برای درک موضوعات مختلف در ریاضیات و همچنین در سایر علوم هستند.

تناسب در حل بسیاری از مسائل زندگی روزمره مانند تجارت هنگام انجام معاملات یا هنگام پخت‌و‌پز و غیره کاربرد دارد. تناسب بین دو یا چند نسبت رابطه برقرار می‌کند و در نتیجه به مقایسه آن‌ها کمک می‌کند.

علامت تناسب در ریاضی چیست؟

طبق تعریف تناسب در ریاضی، وقتی دو نسبت هم‌ارزند یا مساوی یا معادل، با هم تناسب دارند. تناسب در ریاضی معادله یا عبارتی است که برای نشان دادن مساوی بودن دو نسبت یا کسر استفاده می‌شود. با توجه به تناسب، اگر دو مجموعه از اعداد داده‌شده در یک نسبت مساوی افزایش یا کاهش داشته باشند، آنگاه نسبت‌ها به طور مستقیم با یکدیگر تناسب دارند. در اغلب متون، تناسب با نماد "::" یا "=" نشان داده می‌شود.

برای مثال، دو نسبت $$\frac 12$$ و $$\frac 5 {10}$$ تناسب دارند و می‌توان این تناسب را به‌صورت زیر نوشت:

$$\frac 12 :: \frac 5 {10}$$   یا   $$\frac 12 = \frac 5 {10}$$

همان‌طور زمانی که دو نسبت برابر باشند، می‌گوییم دو نسبت با هم تناسب دارند یا با هم متناسب هستند. برای مثال، اگر یک قطار برای پیمودن ۵۰ کیلومتر یک ساعت صرف کند، در طی ۵ ساعت مسافت ۲۵۰ کیلومتری طی می‌کند. و می‌نویسیم: ۵۰ کیلومتر در ۱ ساعت = ۲۵۰ کیلومتر در ۵ ساعت.

تناسب مسلسل

اگر سه نسبت داشته باشیم که بین اولی و دومی تناسب برقرار باشد و بین دومی و سومی نیز تناسب برقرار باشد، می‌گوییم «تناسب مسلسل» داریم. در این صورت، بین نسبت اول و سوم نیز تناسب برقرار است. به همین ترتیب، برای چهار نسبت و بیشتر نیز می‌توانیم موارد مشابهی را بیان کنیم.

برای مثال، سه نسبت $$\frac ab$$ و $$\frac cd$$ و $$\frac ef$$ را در نظر بگیرید. اگر $$\frac ab = \frac cd$$ و $$\frac cd = \frac ef$$، آنگاه می‌توان نتیجه گرفت $$\frac ab = \frac e f$$.

چند نکته درباره تناسب

در ادامه، چند نکته کاربردی را درباره تناسب بیان می‌کنیم که در حل مسائل مختلف کاربرد دارند.

• اگر تناسب $$\frac a b = \frac cd$$‌ را داشته باشیم، آنگاه با توجه به طرفین وسطین، می‌توان نوشت: $$ad = bc$$.
• اگر تناسب $$\frac a b = \frac cd$$‌ را داشته باشیم، آنگاه می‌توان جای صورت و مخرج را در دو کسر تغییر داد و تناسب $$\frac b a = \frac dc$$ را نوشت.
• اگر تناسب $$\frac a b = \frac cd$$‌ را داشته باشیم، آنگاه می‌توان تناسب $$\frac ac = \frac b d$$ را نوشت.
• اگر تناسب $$\frac a b = \frac cd$$‌ را داشته باشیم، آنگاه تناسب $$\frac {a+b}{ b } = \frac {c+ d } d$$ را نیز داریم.
• اگر تناسب $$\frac a b = \frac cd$$‌ را داشته باشیم، آنگاه تناسب $$\frac {a-b}{ b } = \frac {c- d } d$$ را نیز داریم.

یادآوری: اگر هر دو عدد $$a$$ و $$b$$ در نسبت $$\frac a b$$ ذر یک عدد ضرب یا بر یک عدد تقسیم شوند، نسبت حاصل بدون تغییر می‌ماند.

فرمول تناسب

«فرمول تناسب» شاید عبارت درستی نباشد، اما استفاده از آن هنگام محاسباتی که در آن‌ها از تناسب استفاده می‌شود، رایج است. منظور فرمول تناسب معادله‌ای است که برای به‌دست آوردن مقادیر با استفاده از تناسب استفاده می‌شود. برای حل مسائل تناسب، از این مفهوم استفاده می‌کنیم که تناسب دو نسبت است که با یکدیگر برابر هستند. منظور این است که دو کسر با هم برابر باشند.

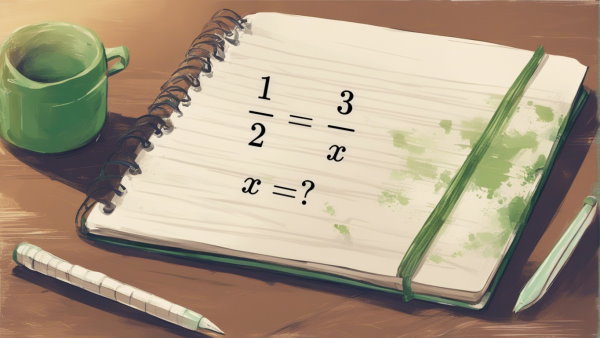
برای مثال، فرض کنید نسبت $$\frac 1 2$$ را داریم که همان ۱ به ۲ است. می‌خواهیم ببینی نسبت ۳ به چه عددی یه تناسب با این نسبت می‌سازد. این گفته را می‌توان به‌صورت معادله زیر نوشت:

$$\frac 1 2 = \frac 3 ?$$

در ریاضیات، معمولاً به‌جای علامت سؤال فرمول بالا از حرف انگلیسی $$x$$ استفاده می‌شود. بنابراین، تناسب را می‌توان به‌فرم معادله زیر نوشت:

$$\frac 1 2 = \frac 3 x$$

تفاوت بین نسبت و تناسب

نسبت و تناسب مفاهیمی نزدیک به هم هستند. تناسب بیانگر رابطه مساوی بین دو یا چند نسبت است. برای درک مفهوم نسبت و تناسب، جدول زیر را آورده‌ایم.

تناسب با شکل

به شکل زیر دقت کنید. می‌خواهیم نسبت قسمت رنگ‌شده آبی به کل شکل را بنویسیم. همان‌طور که می‌بینیم این شکل به سه قسمت مساوی تقسیم شده و از این سه بخش دو تای آن‌ها رنگ شده است. بنابراین، نسبت ۲ به ۳ است و می‌توانیم آن را به‌شکل کسری $$\frac 23$$ بنویسیم.

اکنون شکل زیر را در نظر بگیرید.

این شکل همان شکل قبل است که با رسم خطوط موازی آن را به ۱۵ قسمت مساوی تقسیم کرده‌ایم. نسبت همان نسبت قبلی است، اما در این شکل تعداد خانه‌های آبی کوچک ۱۰ عدد است. بنابراین، نسبت ۱۰ به ۱۵ است که به‌شکل کسری $$\frac {10}{15}$$ نوشته می‌شود. بنابراین، دو کسر یا نسبت $$\frac 2 3$$ و $$\frac { 10 } { 15 }$$ با هم تناسب دارند.

فیلم آموزش نقاشی – ویژه کودکان در فرادرس

کلیک کنید

مثال‌های تناسب در ریاضی

در این بخش، مثال‌های متنوعی از تناسب را حل می‌کنیم.

مثال اول تناسب در ریاضی

آیا مقدارهای داده شده در هر بخش با هم تناسب دارند؟

• ۴۰۰ کیلومتر در مدت ۸ ساعت
• ۱۲۰ کیلومتر در مدت ۲ ساعت

جواب: ۲ ساعت در ۴ ضرب شده و به ۸ ساعت تبدیل شده است. اما اگر ۱۲۰ را در ۴ ضرب کنیم به عدد ۴۸۰ کیلومتر می‌رسیم. می‌بینیم که این دو نسبت تناسب ندارند. اگر بخواهیم این دو ناسب داشته باشند، برای مثال، می‌توانیم از جدول تناسب زیر استفاده کنیم.

بنابراین، دو نسبت زیر با هم تناسب دارند:

• ۴۸۰ کیلومتر در مدت ۸ ساعت
• ۱۲۰ کیلومتر در مدت ۲ ساعت

مثال دوم تناسب در ریاضی

جدول‌های تناسب زیر را کامل کنید.

الف:

ب:

ج:

د:

جواب: کافی است ببینیم صورت یا مخرج در چه عددی ضرب یا بر چه عددی تقسیم شده‌اند تا جواب را به‌دست آوریم. در جدول‌های زیر این مورد را با رنگ قرمز نشان داده‌ایم.

الف:

ب:

ج:

د:

مثال سوم تناسب در ریاضی

نسبت پول احمد به صدرا ۴ به ۷ است. اگر پول احمد برابر با ۲۷٬۰۰۰ تومان باشد، مقدار پول صدرا را محاسبه کنید.

جواب: می‌توانیم از تناسب کمک بگیریم. بدین منظور، جدول تناسب زیر را تشکیل می‌دهیم.

باید ببینیم که عدد ۴ در چه عددی ضرب شده که به ۲۷٬۰۰۰ تبدیل شده است. این عدد به‌صورت زیر محاسبه می‌شود:

$$\frac {27000} 4 = 6750$$

بنابراین، پول صدرا به‌شکل زیر محاسبه می‌شود.

بنابراین، پول صدرا ۴۷٬۲۵۰ تومان است. 

مثال چهارم تناسب در ریاضی

نسبت قد مهسا به پدرش ۵ به ۷ است. اگر قد مهسا ۵۰ سانتی‌متر از قد پدرش کوچک‌تر باشد،‌ قد مهسا و پدرش را محاسبه کنید.

جواب: این مثال را می‌توانیم با تناسب حل کنیم. این بار از کسرها استفاده می‌کنیم:

$$\frac 57$$ = نسبت قد مهسا به پدرش

قد مهسا را برابر با $$x$$ فرض می‌کنیم. همان‌طور که در صورت سؤال گفته شده، قد پدر مهسا ۵۰ سانتی‌متر بیشتر از مهسا است. با توجه به اینکه قد مهسا را برابر با $$x$$ در نظر گرفته‌ایم، قد پدر مهسا برابر با $$x + 50$$ خواهد بود. در نتیجه، می‌توانیم تناسب زیر را بنویسیم:

$$\frac 5 7 = \frac x { x + 50 }$$

برای به‌دست آوردن $$x$$ که همان قد مهسا است، کافی است از طرفین وسطین استفاده کنیم. در نتیجه، خواهیم داشت:

$$5 \times (x+50) = 7 \times x$$

بنابراین، می‌توان نوشت:

$$\begin {align} 5 \times x+5 \times 50 & = 7 \times x \\ 5 x + 250 & = 7 x \\ 250 & = 7 x - 5 x \\250 & = 2 x \\ \frac {250} 2 & = \frac { 2 x } 2 \\ 125 & = x \end {align}$$

در نتیجه، قد مهسا برابر با ۱۲۵ سانتی‌متر است. قد پدرش نیز که ۵۰ سانتی‌متر بیشتر است، برابر با ۱۷۵ = ۵۰ + ۱۲۵ خواهد بود.

مثال پنجم تناسب در ریاضی

نسبت مقدار شکر به آرد در یک کیک ۲ به ۴ است. می‌خواهیم کیکی درست کنیم که مجموع مواد آن ۱۲ پیمانه از مخلوط آرد و شکر داشته باشد. محاسبه کنید که به چند پیمانه آرد و شکر نیاز داریم.

جواب: فرض می‌کنیم تعداد پیمانه‌های آرد برابر با $$x$$ باشد. بنابراین، تعداد پیمانه‌های شکر برابر با $$12 - x$$ است. نسبت شکر به آرد برابر با $$\frac 2 4$$ است. بنابراین، می‌توان نوشت:

$$\frac 2 4 = \frac { 12 - x } { x }$$

با استفاده از طرفین وسطین، می‌توان نوشت:

$$2 \times x = 4 \times (12 - x )$$

در نتیجه، مقدار $$x$$ به‌صورت زیر محاسبه می‌شود:

$$\begin {align} 2 x & = 4 \times 12 - 4 \times x \\ 2 x & = 48 - 4x \\ 2 x + 4 x & = 48 \\ 6 x & = 48 \\ \frac { 6 x } 6 & = \frac { 48 } 6 \\ x & = 8 \end{align}$$

در نتیجه، تعداد پیمانه‌های آرد برابر با ۸ و تعداد پیمانه‌های شکر ۴ = ۸ - ۱۲ است.

مثال ششم تناسب در ریاضی

شکل زیر را در نظر بگیرید. همان‌طور که می‌بینید، در این شکل دو مستطیل مشخص شده است. نسبت مساحت مستطیل کوچک به مساحت مستطیل بزرگ را بنویسید. همچنین، یک نسبت دلخواه بنویسید که با این نسبت تناسب داشته باشد. مساحت هر خانه کوچک را ۱ واحد مربع در نظر بگیرید.

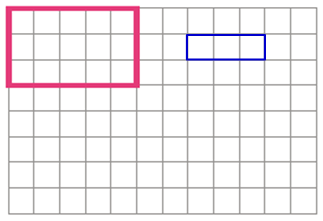
حل: مساحت‌ها برابر با تعداد خانه‌های درون هر مستطیل است. در نتیجه، خواهیم داشت:

• مساحت مستطیل کوچک:  ۳
• مساحت مستطیل بزرگ: ۱۵

بنابراین، نسبت مساحت مستطیل کوچک به مساحت مستطیل بزرگ ۳ به ۱۵ یا $$\frac 3 {15 }$$ است. برای نوشتن کسر معادل، می‌توانیم صورت و مخرج را بر ۳ تقسیم کنیم:

$$\frac 3 { 15 } = \frac {3 \div 3 }{15\div 3} = \frac 1 5$$

بنابراین، $$\frac 3 { 15 }$$ و $$\frac 15$$ نسبت های مساوی هستند.

جمع‌بندی

در این آموزش، با تناسب در ریاضی آشنا شدیم و تفاوت‌های آن با نسبت را شرح داریم. همچنین، مثال‌های متنوعی از تناسب را حل کردیم.