برنامه ریزی پویا — از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، با کنترل بهینه آشنا شدیم. حل معادلاتی که در رگولاتورهای مرتبه دوم خطی به دست آوردیم، تحت شرایط غیر از حالت ماندگار کار دشواری است. در این موارد می‌توان از روش‌های عددی استفاده کرد. یکی از این روش‌ها، برنامه ریزی پویا (Dynamic Programming) است که می‌توان به راحتی آن را به مسئله گسسته رگولاتور مرتبه دوم خطی (LQR) اعمال کرد. برنامه‌ریزی پویا یک روش کارآمد برای حل انواع خاصی از مسائل بهینه‌سازی است و اولین بار، «ریچارد بلمن» (Richard Bellman) آن را ارائه کرد.

روش برنامه ریزی پویا انعطاف‌پذیری بالایی دارد و می‌توان از آن برای حل مسائل متنوعی استفاده کرد. از این مسائل می‌توان به مسیریابی، صرف کمترین هزینه در جابه‌جایی بین دو شهر، برنامه‌ریزی موجودی، کنترل بهینه و... اشاره کرد. هدف اصلی در برنامه ریزی پویا محاسبه یک تابع هزینه در هر حالت است. وقتی نقشه این تابع هزینه به دست آید، قانون کنترل بهینه را می‌توان از یک حالت به حالت دیگر که هزینه را کمینه می‌کند به دست آورد. مسئله عمومی برنامه‌ریزی پویا را می‌توان به صورت زیر نمایش داد:

$$ \large J ( x [ k ] ) = \underbrace { m i n } _ { u [ k ] } \left [ L ( x [ k ] , u [ k ] , x [ k + 1 ] ) + J ( x [ k + 1 ] ) \right ] $$

در بسیاری از موارد، عبارت بالا به صورت زیر اصلاح می‌شود:

 $$ \large J ( x [ k ] ) = \underbrace { m i n } _ { u [ k ] } \left [ L ( x [ k ] , u [ k ] , x [ k + 1 ] ) + \gamma J ( x [ k + 1 ] ) \right ] $$

عامل $$ \gamma $$ مقادیر آینده هزینه رو به جلو را کاهش می‌دهد. اگر $$ \gamma = 0 $$، آنگاه در الگوریتم، از مقدار هزینه رو به جلو کاملاً چشم‌پوشی می‌شود، در حالی که اگر $$ \gamma$$ بزرگ باشد، مقادیر آینده مورد توجه بیشتری قرار می‌گیرند. وجود $$ \gamma$$ در آن دسته از روش‌های عددی نیز مفید است که در آن‌ها مقدار هزینه رو به جلو را برای شروع نمی‌دانیم و آن را به صورت بازگشتی تخمین می‌زنیم. ضریب $$ \gamma$$ اثرات مفروضات اشتباه اولیه را کاهش می‌دهد.

بنابراین، با استفاده از برنامه ریزی پویا حل مسئله کنترل بهینه به یافتن تابع هزینه رو به جلو تقلیل می‌یابد. این کار را می‌توان با حل رو به عقب از حالت مطلوب تا به همه مقادیر اولیه ممکن انجام داد. وقتی این تابع هزینه رو به جلو را یافتیم، قانون کنترل بهینه به یافتن مسیری می‌انجامد که تابع هزینه را از وضعیت فعلی به یک وضعیت آینده کمینه می‌کند. روش برنامه ریزی پویا یک الگوریتم بسیار عمومی است و می‌توان آن را به مسائل بهینه‌سازی اعمال کرد که در آن‌ها هزینه رو به جلو و هزینه جابه‌جایی از یک حالت به حالت دیگر، جمع شونده است. قبل از پرداختن به جزئیات الگوریتم، یک مثال ساده را بیان می‌کنیم.

مثالی از برنامه ریزی پویا

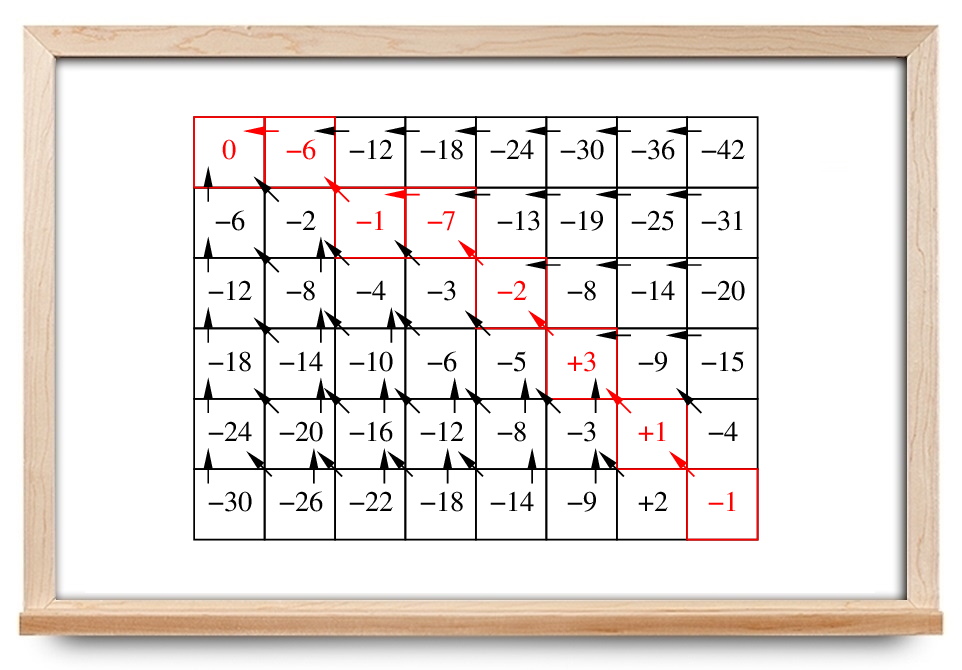
مسئله یافتن کوتاه‌ترین مسیر بین یک هدف و هر نقطه شروع را روی شبکه شکل زیر در نظر بگیرید. فرض می‌کنیم فقط به سمت چپ، راست، بالا و پایین می‌توانیم حرکت کنیم و هر حرکت یک واحد هزینه دارد.

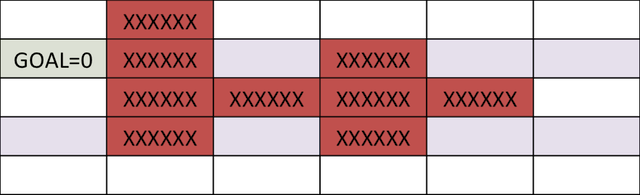
در مثال بالا، محاسبه مسیر بهینه با شروع از شرایط اولیه دشوار است. کار ساده‌تر، محاسبه هزینه رو به جلو با شروع از یک هدف (GOAL) و بازگشت به عقب است. بعد از گام اول، خانه بالا و پایین هدف، هزینه رو به جلویی برابر با ۱ خواهد داشت.

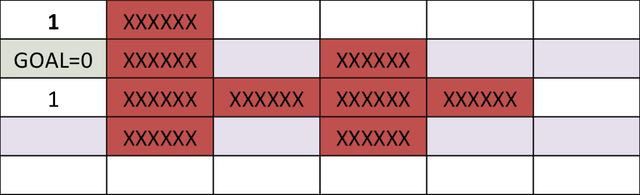
می‌توانیم این گام را برای چهار چرخه بعدی انجام دهیم که در آن، هزینه رو به جلوی متناظر با هر خانه در شکل زیر مشخص شده است. توجه کنید که سلول‌های بالا و سمت راستِ خانه متناظر با ۵ امتیاز، هر دو امتیاز ۶ دارند.

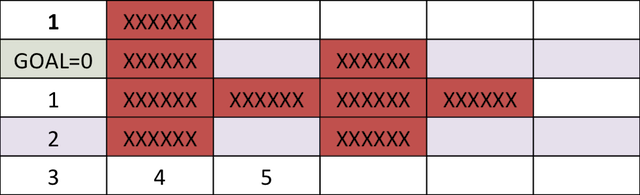
نقشه هزینه رو به جلو برای موقعیت هدف مطابق شکل زیر است.

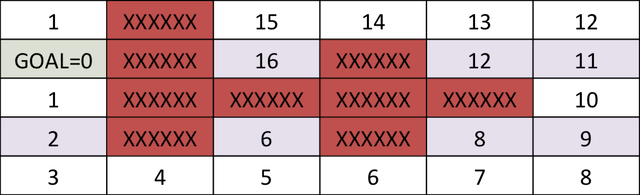
پس از صرف هزینه لازم برای پیکربندی شبکه هدف، می‌توانیم از هر نقطه‌ای از شبکه شروع کرده و با دنبال کردن مسیری که مجموع عمل (۱) و هزینه رو به جلو را کمینه می‌کند، به هدف برسیم. این الگوریتم، همان برنامه ریزی پویا است.

برنامه ریزی پویا برای کنترل رگولاتور خطی درجه دوم

در این بخش روند بالا برای محاسبه کنترل بهینه را برای یک سیستم خطی به فرم زیر بیان می‌کنیم:

$$ \large X [ k ] = A X [ k - 1 ] + B u [ k - 1 ] $$

می‌خواهیم کنترل‌کننده‌ای برای تابع هزینه زیر طراحی کنیم:

$$ \large J ( x [ k ] ) = \underbrace { m i n } _ { u [ k ] } \left [ \frac { 1 } { 2 } \left ( X [ k ] ^ T Q X [ k ] + u [ k ] ^ T R u [ k ] \right ) + J ( x [ k + 1 ] ) \right ] $$

که عبارتِ

$$ \large J ( x [ N ] ) = \frac { 1 } { 2 } X [ N ] ^ T S _ N X [ N ] , $$

هزینه در انتهای هر چرخه است. برنامه‌ریزی پویا را با گام برداشتن به عقب از $$N$$ شروع می‌کنیم:

$$ \large J ( x [ N - 1 ] ) = \underbrace { m i n } _ { u [ N - 1 ] } \left [ \frac { 1 } { 2 } \left ( X [ N - 1 ] ^ T Q X [ N - 1 ] +u [ N - 1 ] ^ T R u [ N - 1 ] \right ) + J ( x [ N ] ) \right ] $$

از آنجایی که $$ J ( x [ N ] ) = \frac { 1 } { 2 } X [ N ] ^ T S _ N X [ N ] $$، داریم:

$$ \large J ( x [ N ] ) = \frac { 1 } { 2 } \left ( A X [ N - 1 ] + B u [ N - 1 ] \right ) ^ T S _ N ( A X [ N - 1 ] + B u [ N - 1 ] ) , $$

بنابراین:

$$ \large J ( x [ N - 1 ] ) = \underbrace { m i n } _ { u [ N - 1 ] } \left [ \frac { 1 } { 2 } \left ( X [ N - 1 ] ^ T Q X [ N - 1 ] + u [ N - 1 ] ^ T R u [ N - 1 ] \right ) \\ \large + \frac { 1 } { 2 } ( A X [ N - 1 ] + B u [ N - 1 ] ) ^ T S _ N ( A X [ N - 1 ] + B u [ N - 1 ] ) \right ] $$

توجه کنید که $$ x[N-1] $$ به $$ u[N-1] $$ وابسته نیست. بنابراین، هزینه رو به جلوی بهینه را می‌توان با استفاده از مشتقات ماتریسی و مشتق‌گیری نسبت به $$ u[N-1] $$ محاسبه کرد:

$$ \large \frac { \partial J ( x [ N - 1 ] ) } { \partial u [ N - 1 ] } = \left [ u [ N - 1 ] ^ T R + ( A X [ N - 1 ] + B u [ N - 1 ] ) ^ T S _ N B \right ] = 0 $$

از آنجایی که $$R$$ و $$ S _ N $$ متقارن هستند، می‌توان نوشت:

$$ \large R u [ N - 1 ] + B ^ T S _ N ( A X [ N - 1 ] + B u [ N - 1 ] ) = 0 $$

$$ \large u [ N - 1 ] = - ( R + B ^ T S _ N B ) ^ { - 1 } B ^ T S _ N A X [ N - 1 ] $$

کنترل بالا را می‌توان به صورت $$ u[N-1] = - K_{N-1} X[N-1] $$ نوشت که در آن:

$$ \large K _ { N - 1 } = ( R + B ^ T S _ N B ) ^ { - 1 } B ^ T S _ N A X [ N - 1 ] $$

اکنون تابع هزینه $$ J(x[N-1]) $$ را می‌توان به صورت زیر نوشت:

$$ \large J ( x [ N - 1 ] ) = \left [ \frac { 1 } { 2 } \left ( X [ N - 1 ] ^ T Q X [ N - 1 ] + u [ N - 1 ] ^ T R u [ N - 1 ] \right ) + J ( x [ N ] ) \right ] $$

$$ \large J ( x [ N - 1 ] ) = \frac { 1 } { 2 } \left [ \left ( X [ N - 1 ] ^ T Q X [ N - 1 ] + X [ N - 1 ] ^ T K _ { N - 1 } ^ T R K _ { N - 1 } u [ N - 1 ] \right ) \\ \large + X [ N - 1 ] ^ T ( A - B K _ { N - 1 } ) ^ T S _ N ( A - B K _ { N - 1 } X [ N - 1 ] ) \right ] $$

اگر $$ J(x[N-1] ) $$ را به صورت $$ \frac{1}{2} X[N-1]^T S_{N-1} X[N-1] $$ بنویسیم، آنگاه:

$$ \large S _ { N - 1 } = Q + K _ { N - 1 } ^ T R K _ { N - 1 } + ( A - B K _ { N - 1 } ) ^ T S _ N ( A - B K _ { N - 1 } ) $$

عبارت بالا همان معادله ریکاتی است که قبلاً‌ درباره آن صحبت کردیم و در آن $$S$$ به جای $$P$$ قرار گرفته است. اکنون عبارت هزینه رو به جلو بین $$ ( N-2) $$ و $$ ( N-1) $$ برابر است با:

$$ \large J ( x [ N - 2 ] ) = \frac { 1 } { 2 } \underbrace { m i n } _ { u [ N - 2 ] } \left [ \left ( X [ N - 2 ] ^ T Q X [ N - 2 ] + u [ N - 2 ] ^ T R u [ N - 2 ] \right ) + J ( x [ N - 1 ] \right ] $$

که در آن:

$$ \large J ( x [ N - 1 ] ) = \frac { 1 } { 2 } X [ N - 1 ] ^ T S _ { N - 1 } X [ N - 1 ] , $$

برنامه‌ریزی پویا برای سیستم‌های پیوسته شامل گسسته‌سازی هزینه رو به جلو با محاسبه هزینه بین یک بازه و بازه بعدی به عنوان انتگرال هزینه کنترل است.

مثال برنامه ریزی پویا برای LQR

سیستمی با معادله $$ \ddot{x} = u $$ را در نظر بگیرید. می‌خواهیم کنترلی را پیدا کنیم که تابع هزینه زیر را کمینه کند:

$$ \large J = \frac { 1 } { 2 } \int _ { u = 0 } ^ 1 u ^ 2 d t $$

که هزینه نهایی برای کمینه شدن برابر است با:‌

$$ \large J _ f = \frac { 1 } { 2 } ( 1 0 x ^ 2 + 1 0 \dot { x } ^ 2 ) $$

با گسسته‌سازی سیستم، مسئله را به برنامه‌‌ریزی پویا تبدیل می‌کنیم:

$$ \large
\frac { d } { d t } \left [ \begin {array} { c } x _ 1 \\ x _ 2 \end {array} \right ] =\left [ \begin {array} {cc} 1 & d t \\ 0 & 1 \end {array} \right ] \left [ \begin {array} { c } x _ 1 \\ x _ 2 \end {array} \right ] + \left [ \begin {array} { c } 0 \\ d t \end {array} \right ] u $$

اکنون، پارامترهای متناظر با هزینه رو به جلو، $$ S_N = 10I $$، $$ Q = 0 $$ و $$ R = dt $$ هستند. از معادلات زیر برای محاسبه بازگشتی $$S_N$$ استفاده می‌کنیم و از حالت‌ها رو به جلو انتگرال می‌گیریم برای محاسبه کنترل بهینه. در عمل، $$Q = 0 $$ نتایج عددی را ارائه می‌دهد که ناپایدار هستند، بنابراین، از $$ Q = 0.001 dt I $$ استفاده می‌کنیم.

$$ \large K _ { N - 1 } = ( R + B ^ T S _ N B ) ^ { - 1 } B ^ T S _ N A X [ N - 1 ] $$

$$ \large S _ { N - 1 } = Q + K _ { N - 1 } ^ T R K _ { N - 1 } + ( A - B K _ { N - 1 } ) ^ T S _ N ( A - B K _ { N - 1 } ) $$

1clc
2close all
3clear all 
4
5t_f = 4;
6dt = 0.02;
7t_dis = 0:dt:t_f;
8N = length(t_dis);
9S{N} = 100*eye(2);
10R = dt;
11Q = .0001*eye(2)*dt;
12A = [1 dt;0 1];
13B = [0 ;dt];
14K{N} = [0 0];
15K_norm(N)=0;
16
17for i = N-1:-1:1
18    K{i} = inv(R + B'*S{i+1}*B)*B'*S{i+1}*A;
19    S{i} = Q + K{i}'*R*K{i} + (A-B*K{i})'*S{i+1}*(A-B*K{i});
20    K_norm(i) = norm(K{i});
21end
22
23X(:,1) = [1;0];
24X_dlqr(:,1) = [1;0];
25P_dlqr = idare(A,B,Q,R);
26K_dlqr = inv(R)*B'*P_dlqr;
27
28for i = 1:N-1
29    u(i) = -K{i}*X(:,i);
30    X(:,i+1) = A * X(:,i) + B*u(i);
31    X_dlqr(:,i+1) = A * X_dlqr(:,i) - B*K_dlqr*X_dlqr(:,i) ;
32
33end
34
35figure;
36subplot(2,1,1)
37plot(t_dis,X(1,:),t_dis,X_dlqr(1,:))
38legend('DyP','LQR')
39ylabel('position')
40subplot(2,1,2)
41plot(t_dis,X(2,:),t_dis,X_dlqr(2,:))
42legend('DyP','LQR')
43ylabel('velocity')
44xlabel('time')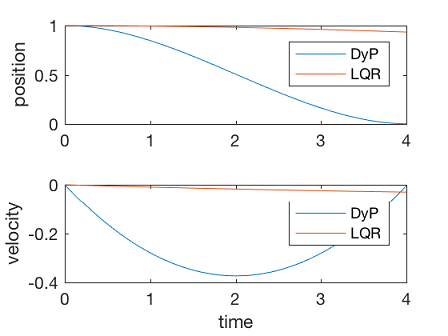

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترل بهینه
• مجموعه آموزش‌های مهندسی برق
• آموزش کنترل مدرن – حل ۱۰۰ مساله
• کنترل بهینه گسسته — پیاده‌سازی در متلب
• تشخیص عیب (Fault Detection) — از صفر تا صد
• کنترل تطبیقی — از صفر تا صد

^^