در آموزش‌های قبلی مجله فرادرس، با مفاهیم کنترل بهینه و پیاده‌سازی آن در متلب آشنا شدیم. در این آموزش، درباره کنترل بهینه گسسته بحث خواهیم کرد. پیشنهاد می‌کنیم قبل از مطالعه این مطلب، آموزش «کنترل بهینه در متلب» را مطالعه کنید.
کنترل بهینه گسسته
معادله دینامیکی سیستم زیر را در نظر بگیرید:
$$ \large X [ k + 1 ] = f ( x [ k ] , u [ k ] ) $$
که شرایط اولیه آن، $$ X[1] = X_0 $$ است.
می‌خواهیم کنترل $$ u[k] $$ را به گونه‌ای پیدا کنیم که تابع هزینه زیر را کمینه کند:
$$ \large J ( u ) = \Phi ( X _ f ) + \sum _ { k =1 } ^ { N } L ( X [ k ] , u [ k ] ) . $$
مشابه عملیاتی که برای یک مسئله پیوسته‌زمان در آموزش قبلی انجام دادیم، همیلتونین $$ H(X,u,\lambda ) $$ را به صورت زیر می‌نویسیم:
$$ \large H ( X [ k ] , u[ k ] , \lambda [ k + 1 ] ) = L ( X [ k ] , u [ k ] ) + \lambda [ k + 1 ] ^ T f ( x [ k ] , u [ k ] ) $$
در این حالت، شرایط بهینگی به صورت زیر خواهند بود:
$$ \large \left . \frac { \partial H } { \partial X } \right | _ { X [ k ] , u[ k ] , \lambda [ k + 1 ] } ^ T = \lambda [ k ] $$
$$ \large \left . \frac { \partial H } { \partial u } \right | _ { X [ k ] , u [ k ] , \lambda [ k + 1 ] } = 0 $$
$$ \large \left . \frac { \partial \Phi } { \partial X } \right | _ { X _ f } = \lambda _ f $$
رگولاتور خطی و گسسته درجه دوم با زمان محدود
معادله دینامیکی سیستم خطی زیر را در نظر بگیرید:
$$ \large X [ k + 1 ] = A x [ k ] + B u [ k ] $$
که شرایط اولیه آن $$ X[1] = X_0 $$ است.
هدف، یافتن $$ u[k] $$ است که تابع هزینه زیر را کمینه کند:
$$ \large J ( u ) = \frac { 1 } { 2 } X _ f ^ T S X _ f + \frac { 1 } { 2 } \sum _ { k = 1 } ^ { N } \left ( X [ k ] ^T Q X [ k ] + u [ k ] ^ T R u [ k ] \right ) . $$
با طی مراحلی مشابه آموزش کنترل بهینه، می‌توان نشان داد که شرایط لازم بهینگی به صورت زیر خواهند بود:
$$ \large \begin{align*}
u [ k ] & = – R ^ { – 1 } B ^ T \lambda [ k + 1 ] \\
\lambda [ k ] & = A ^ T \lambda [ k + 1 ] + Q X [ k ] \\
X [ k + 1 ] & = A x [ k ]+ B u [ k ]
\end {align*} $$
و شرایط مرزی $$ X[1] = X_0 $$ و $$ \lambda[N+1] = S X_f $$ هستند.
از آنجا که معادلات در $$X$$ و $$u$$ خطی هستند، به دنبال جوابی به فرم زیر خواهیم بود:
$$ \large \lambda [ k ] = P [ k ] X [ k ] $$
با جایگذاری
$$ \large X[k+1] = Ax[k]+ B u[k] $$
و
$$\large u[k] = – R^{-1} B^T \lambda[k+1] = – R^{-1} B^T P[k+1] X[k+1] $$
در $$ u[k] = – R^{-1} B^T \lambda[k+1]$$، داریم:
$$ \large \begin{align*}
\lambda [ k + 1 ] & = P [ k + 1 ] X[ k + 1 ] = P [ k + 1 ] ( A X [k ] + B u [ k ] ) \\ & = P [ k + 1 ] ( A X [ k ] – B R ^ { – 1 } B ^ T \lambda [ k + 1 ] )
\end {align*} $$
$$ \large ( I + P [ k + 1 ] B R ^ { – 1 } B ^ T ) \lambda [ k + 1 ] = P [ k + 1 ] A X [ k ] $$
$$ \large \lambda [ k + 1 ] = ( I + P [ k + 1 ] B R ^ { – 1 } B ^ T ) ^ { – 1 } P [ k + 1 ] A X [ k ] $$
با جایگذاری در معادله انتشار کمک‌حالت، خواهیم داشت:
$$ \large \begin{align*}
P [ k ] X [ k ] & = A ^ T \left ( ( I + P [ k + 1 ] B R ^ { – 1 } B ^ T ) ^ { – 1 } P [ k + 1 ] A X [ k ] \right ) + Q X [ k ] \\
P [ k ] X [ k ] & = A ^ T ( I + P [ k + 1 ] B R ^ { – 1 } B ^ T ) ^ { – 1 } P[ k + 1 ] A X [ k ] + Q X [ k ]
\end {align*} $$
از آنجایی که معادله بالا برای همه $$ X[k]$$ها برقرار است، داریم:
$$ \large P [ k ] = A ^ T ( I + P [ k + 1 ] B R ^ { – 1 } B ^ T ) ^ { – 1 } P [ k +1 ] A + Q $$
فرم دیگر
معادلات گسسته را می‌توان به صورت زیر نیز به دست آورد:
$$ \large u [ k ] = – R ^ { – 1 } B ^ T \lambda [ k + 1 ] $$
$$ \large R u [ k ] = – B ^ T P [ k + 1 ] X [ K + 1 ] $$
$$ \large R u [ k ] = – B ^ T P [ k + 1 ] ( A X [ k ] + B u [ k ] ) $$
$$ \large ( R + B ^ T P [ k + 1 ] B ) u [ k ] = – B ^ T P [ k + 1 ] A X [ k ] $$
$$ \large u [ k ] = – ( R + B ^ T P [ k + 1 ] B ) ^ { – 1 } B ^ T P [ k + 1] A X [ k ] $$
معادلات کمک‌حالت نیز برابرند با:
$$ \large \lambda [ k ] = A ^ T \lambda [ k + 1 ] + Q X [ k ] $$
$$ \large \lambda [ k ] = A ^ T P [ k + 1 ] X [ k + 1 ] + Q X [ k ] $$
$$ \large \lambda [ k ] = A ^ T P [ k + 1 ] ( A X [ k ] + B u [ k ] ) + Q X [ k ] $$
$$ \large P [ k ] X [ k ] = A ^ T P [ k +1 ] ( A – B ( R + B ^ T P [ k + 1 ] B ) ^ { – 1 } B ^ T P [ k + 1 ] A ) X [ k ] + Q X [ k ] $$
از آنجایی که رابطه بالا برای همه $$X[k] $$ها برقرار است، داریم:
$$ \large P [ k ] = A ^ T P [ k + 1 ] A – A ^ T P [ k + 1 ] B ( R + B ^ T P [ k + 1 ] B ) ^ { – 1 } B ^ T P [ k + 1 ] A + Q $$
رگولاتور خطی و گسسته درجه دوم با زمان نامحدود
معادله یک سیستم خطی دینامیکی را با شرایط اولیه $$X[1] = X_0 $$ به صورت زیر در نظر بگیرید:
$$ \large X [ k + 1 ] = A x [ k ]+ B u [ k ] $$
هدف، یافتن $$ u[k] $$ است که تابع زیر را کمینه کند:
$$ \large J ( u ) = \sum _ { k = 1 } ^ { \infty } \left ( X [ k ] ^ T Q X [ k ] + u [ k ] ^ T R u [ k ] \right ) . $$
تحت شرایط حالت ماندگار یا فرض زمان بی‌نهایت، $$ P[k] = P[k+1] $$ و معادله ریکاتی به رابطه زیر کاهش می‌یابند:
$$ \large P = A ^ T + A ^ T ( I + P B R ^ { – 1 } B ^ T ) ^ { – 1 } P A + Q $$
با توجه به فرمول دوم، معادله ریکاتی را می‌توان به صورت زیر نوشت:
$$ \large P = A ^ T P A – A ^ T P B ( R + B ^ T P B ) ^ { – 1 } B ^ T P A + Q $$
توجه کنید که دو فرم معادله ریکاتی معادل هستند و با استفاده از لم معکوس ماتریس می‌توان هر یک را به دیگری تبدیل کرد.
جواب معادله ریکلاتی جبری گسسته را می‌توان با استفاده از دستور “dare” در متلب پیاده‌سازی کرد:
clc
close all
clear all
t_f = 20;
dt = 0.0001;
t_dis = 0:dt:t_f;
N = length(t_dis);
S{N} = 100*eye(2);
R = dt;
Q = .0001*eye(2)*dt;
A = [1 dt;0 1];
B = [0 ;dt];
K{N} = [0 0];
for i = N-1:-1:1
%K{i} = inv(R + B'*S{i+1}*B)*B'*S{i+1}*A;
%S{i} = Q + K{i}'*R*K{i} + (A-B*K{i})'*S{i+1}*(A-B*K{i}); % First form
%S{i} = Q+ A'*S{i+1}*A - A'*S{i+1}*B*inv(R+B'*R*B)*B'*S{i+1}*A;% Second form
S{i} = A'*inv(eye(2) + S{i+1}*B*inv(R)*B')*S{i+1}*A + Q; % Third form
K_norm(i) = norm(K{i});
end
X(:,1) = [1;0];
X_dlqr(:,1) = [1;0];
P_dlqr = dare(A,B,Q,R);
K_dlqr = inv(R)*B'*P_dlqr;
for i = 2:N
u(i-1) = -inv(R)*B'*S{i-1}*X(:,i-1);
X(:,i) = A * X(:,i-1) + B*u(i-1);
X_dlqr(:,i) = A * X_dlqr(:,i-1) - B*K_dlqr*X_dlqr(:,i-1) ;
end
figure;
subplot(2,1,1)
plot(t_dis,X(1,:),t_dis,X_dlqr(1,:))
legend('DyP','LQR')
ylabel('position')
subplot(2,1,2)
plot(t_dis,X(2,:),t_dis,X_dlqr(2,:))
legend('DyP','LQR')
ylabel('velocity')
xlabel('time')
نتیجه اجرای برنامه بالا، نمودارهای زیر خواهد بود:
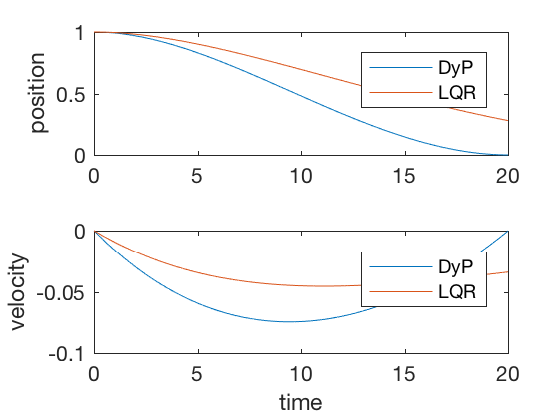
برای زمان به اندازه کافی بزرگ، جواب با زمان نامحدود و LQR با زمان محدود، سیگنال کنترل مشابهی خواهند داشت. البته وقتی زمان نهایی ثابت باشد، روش زمان نامحدود با شکست مواجه می‌شود. شکل زیر مقایسه خروجی‌های زمان محدود و زمان نامحدود را برای زمان‌های نهایی بزرگ نشان می‌دهد. همان‌طور که می‌بینیم، عملکرد کنترل‌کننده در دو حالت برابر است.
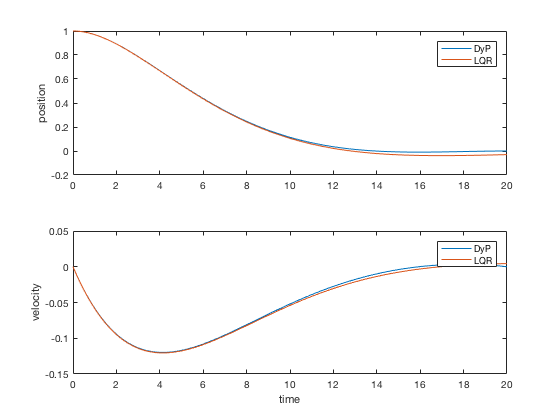
تذکر: جواب LQR با استفاده از توابع “care” و “dare” فقط به مسائلی با زمان نامحدود قابل اعمال هستند.
شرایط لازمی را که کنترل‌کننده بهینه باید در آن صدق کند به دست آوردیم. این شرایط را به مسائل LQR گسسته اعمال کردیم و یک روش محاسبه کنترل بهینه را برای خطای صفر در زمان محدود دیدیم. البته، روش بالا محدودیت‌هایی نیز دارد:
- همه توابع هزینه را نمی‌توان به صورت مسئله LQR بیان کرد. حالتی را در نظر بگیرید که می‌خواهیم زمان را کمینه کنیم.
- فرمول‌بندی‌های LQR برای شرایطی که قیود اضافه به سیستم اعمال شود به خوبی تعمیم‌یافته نیستند.
- برای قیود نامساوی کنترل، جواب کنترل LQR به مقادیری خاصی محدود می‌شود.
- کار با حالت یا ترکیب حالت-کنترل دشوارتر است و شرایط بهینگی منتجه بسیار پیچیده خواهد بود.
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس مهندسی کنترل
- آموزش کنترل بهینه
- مجموعه آموزش‌های مهندسی برق
- آموزش کنترل مدرن – حل ۱۰۰ مساله
- شبکه عصبی در متلب — از صفر تا صد
- تقلب نامه (Cheat Sheet) کنترل خطی
- جایابی قطب — از صفر تا صد
^^
