آنالیز واریانس دو طرفه در اکسل – راهنمای کاربردی
تجزیه و تحلیل یا به اصطلاح «آنالیز واریانس» (Analysis of Variance) یک تکنیک آماری است که با استفاده از تجزیه واریانس به چند بخش، اثر تیمارها روی یک متغیر وابسته را تعیین میکند. در این بین تحلیل یا آنالیز واریانس دو طرفه به علت پیچیدگی محاسباتی کمتر به صورت دستی مورد بهره برداری قرار میگیرد. در این نوشتار از مجله فرادرس به بررسی آنالیز واریانس دو طرفه در اکسل پرداخته و شیوه اجرای آن را به کمک ابزار محاسبات آماری در اکسل (Analysis Toolpack) بازگو خواهیم کرد. البته در نوشتار قبلی از این سری، آنالیز واریانس یک طرفه در اکسل نیز معرفی شد.

پیشنهاد میشود، برای درک بهتر مفاهیم مربوط به تحلیل یا آنالیز واریانس مطلب «جدول آنالیز واریانس» (ANOVA) و «آنالیز واریانس یک طرفه» (One-way ANOVA) را مطالعه کنید. همچنین خواندن نوشتار تحلیل واریانس دو طرفه در پایتون — راهنمای گام به گام و آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی نیز خالی از لطف نیست.
آنالیز واریانس دو طرفه در اکسل
از تکنیک «آنالیز واریانس دو طرفه» (two-way ANOVA) برای ارزیابی و نمایش تفاوت معنیدار بین دو نوع تیمار (با تعداد سطوح مختلف) استفاده میشود. گاهی به این تیمارها، عامل نیز گفته شده و در نتیجه ANOVA دو طرفه را، تحلیل واریانس دو عاملی (Two Factor ANOVA) نیز مینامند.
در این نوشتار، ما از طریق ANOVA دو طرفه و با استفاده از ابزارهای تحلیل آماری اکسل، یک مثال در این زمینه را مورد بررسی قرار داده و نتایج را تفسیر خواهیم کرد.
در این بین از بسته تحلیل یا محاسبات آماری اختصاصی اکسل بهره میبریم. حتی اگر به بسته آماری اکسل (Analysis ToolPak) نیز دسترسی ندارید، باز هم به کارگیری تحلیل واریانس دو طرفه در اکسل قابل اجرا است. کافی است الگوی محاسباتی که در این متن به آن اشاره میشود را به صورت فرمول در سلولها درج کنید، هر چند به کارگیری بسته تحلیل اکسل کار را سادهتر و دقیقتر انجام میدهد.
نکته: توجه داشته باشید که اکسل از این تحلیل به عنوان ANOVA «دو عاملی» (Two Factor ANOVA) یاد میکند.
تحلیل واریانس دو طرفه در حقیقت به کمک یک آزمون فرض پایهریزی میشود که به شما امکان مقایسه میانگینهای گروهی را میدهد. مانند همه آزمونهای فرض، ANOVA دو طرفه از دادههای نمونه برای استنباط خصوصیات کل جمعیت استفاده میکند.
در ادامه به صورت گام به گام و به همراه دو مثال، مراحل اجرای آنالیز واریانس دو طرفه در اکسل را در دو بخش، فرا خواهیم گرفت. بخش اول ANOVA را بدون اثرات متقابل در نظر گفته ولی در قسمت دوم به بررسی مثالی میپردازیم که اثرات متقابل در آن معنیدار بوده و بخصوص تفسیر آن نیاز به درک بهتر و دقیقتر مسئله آنالیز واریانس دو طرفه دارد.
قبل از ادامه، اطمینان حاصل کنید که Analysis ToolPak در برگه Data در نرمافزار اکسل نصب شده است. به منظور آشنایی با نحوه نصب بسته تحلیل آماری اکسل به مطلب آنالیز واریانس یک طرفه در اکسل — راهنمای کاربردی مراجعه کنید. در آنجا مراحل و گامهای نصب این افزونه در اکسل به طور کامل شرح داده شده است. محل قرارگیری این دستور در تصویر ۱، به خوبی مشخص شده است.

گامهای اجرای آنالیز واریانس دو طرفه در اکسل
برای انجام این تجزیه و تحلیل، شما به دو متغیر طبقهبندی نیاز دارید که تحلیلگران اغلب آنها را به عنوان «عامل» (Factor) یاد میکنند. این عوامل متغیرهای مستقل شما هستند. تعداد عوامل در تجزیه و تحلیل، نام تجزیه و تحلیل واریانس را تعیین میکند. در نتیجه آنالیز واریانس یک طرفه مرتبط با یک متغیر عامل است. همچنین آنالیز واریانس دو طرفه دارای دو متغیر عامل یا فاکتور است. در صورتی که چند متغیر عامل وجود داشته باشد، طرح آنالیز واریانس را چند طرفه (Multiway) مینامند. البته چنین حالتی به علت پیچیدگی رابطهها، کمتر به کار میرود.
از طرفی هر عامل دارای تعداد محدودی از مقادیر ممکن است که به عنوان سطوح شناخته میشوند. به عنوان مثال، جنسیت یک عامل یا متغیر طبقهای است که دارای دو سطح زن و مرد است.
در آنالیز واریانس، متغیری که میانگین آن باید مورد سنجش و آزمون قرار گیرد، یک متغیر پیوسته و کمی است که به آن متغیر وابسته (Dependent) نیز گفته میشود. ترکیبات مختلف مقادیر برای دو متغیر طبقهای، دادههای مربوط به متغیر وابسته را به گروههای مجزا تقسیم میکند. آنالیز واریانس دو طرفه در اکسل تعیین میکند که آیا اختلاف میانگین بین این گروهها از نظر آماری معنیدار است یا خیر.
شکل فرضیههای این آزمون درست به مانند آزمون فرض آنالیز واریانس یک طرفه است. البته این موضوع را هم در نظر بگیرید که اثرات متقابل (Interaction) بین متغیرهای عامل نیز در این آزمون، در نظر گرفته و مدل براساس آن ساخته میشود. وقتی اثرات متقابل قابل توجه بوده و از لحاظ آماری معنیدار باشد، تفسیر صحیح آن امری بسیار مهم تلقی میشود. به این منظور در انتهای هر یک از مثالها بخشی را به تفسیر نتایج حاصل اختصاص دادهایم.
همانطور که گفته شد، دو مثال در این متن مورد اشاره قرار میگیرد که در اولی، بدون اثر متقابل و در دومی با اثرات متقابل بین متغیرهای عامل، تحلیل واریانس دو طرفه در اکسل صورت میگیرد. البته دادههای مربوطه ساختگی هستند ولی میتوانید آنها را به مانند دادههای واقعی در نظر بگیرید زیرا به خوبی نتایج توسط این دادهها قابل درک است.
به منظور دریافت این فایل اطلاعاتی که با قالب csv ایجاد شده، کافی است اینجا کلیک کنید تا فایل داده روی رایانه شخصی شما بارگذاری شود. البته فایل دریافتی به صورت فشرده است، پس از خارج کردن آن از حالت فشرده، میتوانید آن را برای اجرای آنالیز واریانس دو طرفه در اکسل باز کنید.
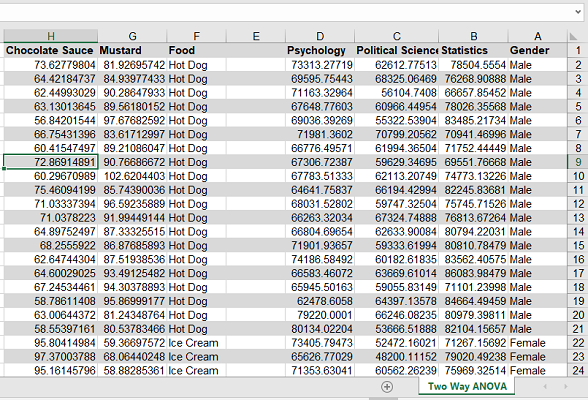
بهتر است ابتدا نگاهی به این مجموعه داده بیندازیم. همانطور که در تصویر ۲، مشاهده میکنید، این کاربرگ از اکسل، دارای ۷ ستون و ۴۰ سطر است که ستون Gender (متغیر جنسیت) نقش متغیرهای طبقهای یا عامل را داشته و بقیه به عنوان متغیر وابسته میتوانند به کار روند. برای مثال ستون Statistics مربوط به متغیر میزان درآمد فردی است که در رشته آمار تحصیل کرده است. ستونهای بعدی در این بخش نیز مربوط به درآمد افراد در رشتههای تحصیلی دیگر است.
توجه داشته باشید که ستونهای A تا D مربوط به مثال یک بوده و ستونهای F تا H نیز به مثال ۲ مرتبط هستند. در نتیجه اطلاعات مربوط به ستونهای F تا H را در بخش مربوط به مثال ۲، معرفی خواهیم کرد.
قبل از آنکه به مثالها بپردازیم در ابتدا نحوه دسترسی به فرمان آنالیز واریانس دو طرفه در اکسل را در جعبه ابزار Data Analysis بررسی میکنیم.
برای باز کردن پنجره تحلیلهای آماری در اکسل، از برگه Data در بخش Analyze دستور Data Analysis را مطابق با تصویر ۱، اجرا کنید. با این کار، پنجرهای با عنوان Data Analysis باز شده که در کادر Analysis Tools، گزینههای ANOVA: Two-Factor With Replication و ANOVA: Two-Factor Without Replication مربوط به آنالیز واریانس دو طرفه در اکسل هستند.
کلمه Replication در انتهای عبارتها به معنی وجود یا عدم اندازههای تکراری است. به این ترتیب اگر همه افراد (موردها) در همه گروهها حضور داشته و مقدار متغیر وابسته برایشان اندازهگیری شود، باید از تحلیل با مقادیر تکراری (With Replication) استفاده کرد. ولی در صورتی که هر فرد فقط در یک گروه جای داشته باشد، تحلیل Without Replication را به کار خواهیم برد.
به عنوان مثال، در اولین مثال تجزیه و تحلیل واریانس در این نوشتار، به بررسی تاثیر جنسیت (Gender) و تحصیلات دانشگاهی روی درآمد فرد، خواهیم پرداخت تا مشخص شود آیا این عوامل با میانگین درآمد شغلی ارتباط دارند یا خیر. در حقیقت این آزمون نشان میدهد که اختلاف میانگین درآمدها با توجه به جنسیت و رشته تحصیلی، معنیدار است یا خیر. اگر در هر گروه فقط یک مشاهده جمعآوری شده بود (به عنوان مثال، یک زن که در رشته آمار تحصیل میکند)، از تحلیل «بدون تکرار» استفاده خواهیم میکردیم. البته این کار، یک نمونه کوچک را تولید میکند. بنابراین، از گزینه «با تکرار» (With Replication) استفاده خواهیم کرد تا بتوانیم مشاهدات متعدد را در هر گروه داشته باشیم. به این ترتیب برای هر دو مثال، ما 20 مشاهده در هر گروه خواهیم داشت.
نکته: تجزیه و تحلیل یا آنالیز واریانس دو طرفه در اکسل فقط به صورت متعادل قابل اجر است. در طراحیهای متعادل، همه گروهها تعداد مشاهدات برابر دارند.
مثال اول: آنالیز واریانس دو طرفه در اکسل بدون اثرات متقابل
تصور کنید که ما در حال ارزیابی حقوق سالانه هستیم که همان متغیر وابسته با مقادیر پیوسته است. دو عامل طبقهبندی در این بین، جنسیت و گرایش دانشگاهی است. برای این تجزیه و تحلیل، ما از سه گرایش آمار (ستون Statistics)، روانشناسی (ستون Psychology) و رشته علوم سیاسی (Political Science) استفاده خواهیم کرد. ترکیبی از این دو عامل (2 جنس × ۳ رشته) شش گروه زیر را ایجاد میکند. توجه داشته باشید که هر گروه شامل 20 مشاهده است.
جدول ۱، طبقهبندی مشاهدات به تفکیک جنسیت و رشته تحصیلی:
| جنسیت / رشته | آمار | روانشناسی | علوم سیاسی |
| مرد | 77743 | 69776 | 62015 |
| زن | 74074 | 65320 | 55195 |
هر کدام از مقادیر درون جدول، درآمد فرد در آن رشته را در یک سال نشان میدهد.
آنالیز واریانس دو طرفه تعیین میکند که آیا تفاوت مشاهده شده بین میانگینها شواهد کافی و قوی برای نتیجهگیری در مورد متفاوت بودن میزان درآمد در بین گروهها در جامعه آماری ارائه میدهد.
به منظور اجرای این آزمون فرض آماری (آنالیز واریانس دو طرفه با مقادیر تکراری) در اکسل مراحل و گامهای زیر را انجام دهید.
- بر روی Analysis Data در برگه Data کلیک کنید.
- از پنجره Analysis Data گزینه Anova: Two-Factor With Replication را انتخاب کنید.
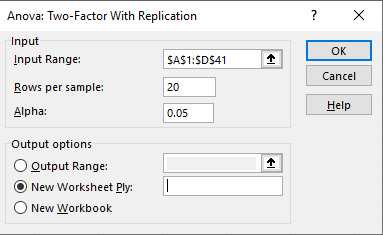
- در بخش Input، قسمت Input Range را با آدرس همه ستونهای داده (متغیرهای رشته تحصیلی و جنسبت) مشخص کنید.
- در قسمت Rows per sample، عدد 20 را وارد کنید. این تعداد مشاهدات در هر گروه را نشان میدهد.
- اکسل از مقدار آلفای (Alpha) پیش فرض 0٫05 برای میزان یا احتمال خطای نوع اول، استفاده میکند که معمولاً مقدار خوبی است. آلفا سطح معنی داری آزمون در نظر گرفته میشود. این مقدار را فقط در صورتی تغییر دهید که دلیل خاصی برای این کار داشته باشید.
- در بخش Output options، گزینه انتخابی New Worksheet Ply مناسب است، زیرا خروجی را در یک کاربرگ جدید نشان خواهد داد. گزینه Output Range، باعث نمایش خروجی در ناحیه انتخابی و New Workbook در یک کارپوشه جدید خواهد شد.
- روی دکمه OK کلیک کنید.
برای این مثال، تصویر زیر نتیجه اجرای این تنظیمات را نشان میدهد.
پس از کلیک روی دکمه OK، خروجی در یک کاربرگ جدید (مثلا sheet2) ساخته میشود. این خروجی شامل دو جدول است. در بخش اول، جدولی از مقادیر مربوط به شاخصهای آماری با نام SUMMARY دیده میشود که شامل تعداد (Count) در هر گروه، جمع مقادیر متغیر وابسته (Sum)، میانگین (Average) و واریانس (Variance) است.
همانطور که دیده میشود، میانگینها در بین گروهها با یکدیگر از لحاظ ریاضی، اختلاف دارند ولی هدف از اجرای آنالیز واریانس آن است که مشخص شود، آیا این اختلافها ناشی از نمونهگیری است یا واقعا در جامعه نیز این تفاوتها وجود دارد. به گروهها که توسط رشته تحصیلی و همچنین جنسیت در این جدول دیده میشود، توجه کنید. به این ترتیب اگر فقط میانگین (Average) را در نظر بگیریم، ۶ مقدار مختلف برحسب گروه یا طبقهها محاسبه و نمایش داده شده است.
جدول SUMMARY، درآمد متوسط شش گروه مورد بررسی را نشان میدهد. این میانگینها از کمترین میزان 55،191 دلار برای رشتههای علوم سیاسی زن تا بالاترین میزان 77،743 دلار برای رشتههای آمار مرد در تغییر است. به طور کلی، مردان درآمد متوسط بیشتری در همه رشتهها دارند. علاوه بر این، افرادی که در گروه یا رشته تحصیلی آماری مشغول به کار هستند، بیشترین متوسط حقوق را دارند. بنابراین میتوان حدس زد که میانگین در بین رشتههای تحصیلی متفاوت است. ولی این کار باید توسط یک آزمون آماری صورت گیرد تا براساس اصول آزمون فرض نسبت به تفاوتها قضاوت کنیم.
نکته: مشخص است که تعداد مشاهدات در هر گروه برابر با ۲۰ تعیین شده است پس آنالیز واریانس متعادل اجرا شده است. یکی از شرطهای مهم در آنالیز برابری واریانسها و توزیع نرمال برای متغیر وابسته است که در این مطلب به آنها نپرداختهایم. برای اطلاعات بیشتر در این زمینه میتوانید نوشتارهای دیگر مجله فرادرس با عنوان آزمون نرمال بودن داده (Normality Test) — پیادهسازی در پایتون را مطالعه کنید.
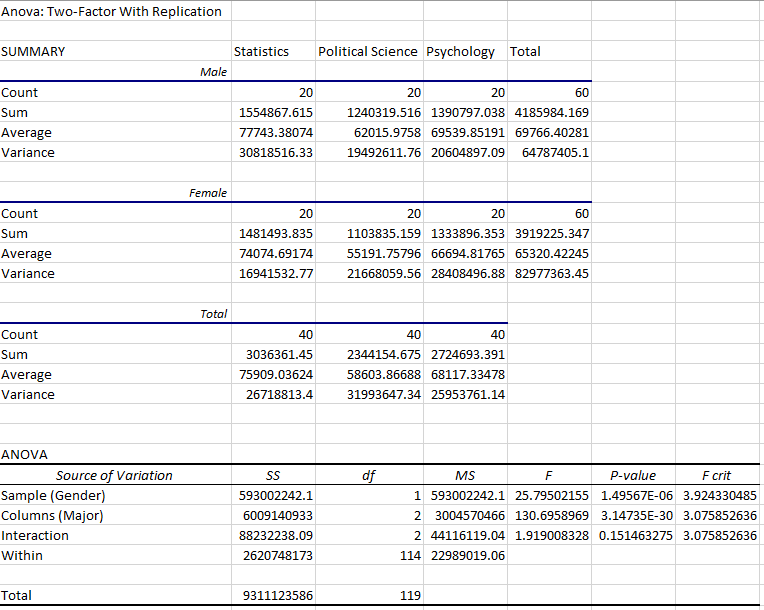
قسمت بعدی مربوط به جدول ANOVA یا همان جدول آنالیز واریانس است. ابتدا برای تشخیص وجود اختلاف آماری در بین میانگینها به ستون P-value یا مقدار احتمال در جدول نگاه کنید. از آنجا که مقادیر P-value برای متغیر جنسیت (سطر Gender) کوچکتر از سطح معناداری (یعنی ۰٫۰۵) است، این عامل (جنسیت) از نظر آماری در اختلاف درآمدی، معنیدار هستند و فرض صفر (برابری همه میانگینها) رد میشود. از طرفی برای ستونها (Major) که نشان از رشته تحصیلی دارد نیز مقدار P-value از خطای نوع اول کوچکتر است. بنابراین عامل رشته تحصیلی نیز در تغییر درآمد تاثیرگذار خواهد بود. این عامل و تأثیرات آنها را «اثرات اصلی» (Main Effect) در مدل مینامند. توجه داشته باشید که این P-value به قدری کوچک است که به صورت نماد عملی نمایش داده شده و بسیار به صفر نزدیک است.
نکته: منظور از 1.49567E-06 مقداری است که در ابتدای ارقام آن، 5 رقم صفر به عنوان ابتدای اعشار داشته، سپس بقیه ارقام اعشار آغاز میشوند.
از طرف دیگر، اثرات متقابل از لحاظ آماری، قابل توجه نیست زیرا «مقدار احتمال» (p-value) برای آن برابر با 0٫151 بوده که بیشتر از سطح معناداری آزمون مورد نظر ما است. از آنجا که اثر متقابل قابل توجه نیست، بنابراین میتوانیم فقط روی اثرات اصلی تمرکز کنیم.
تأثیرات اصلی، بخشی از رابطه بین یک متغیر مستقل و متغیر وابسته است که با ثابت در نظر گرفتن اثر متغیرهای دیگر، تغییر میکند. به عنوان مثال، تأثیر اصلی متغیر یا عامل جنسیت بر درآمد متوسط تاثیر گذار است. مردان درآمد متوسط بالاتری دارند و این تأثیر در تمام رشتههای تحصیلی دیده میشود. البته توجه داشته باشید که از لحاظ ریاضی اختلاف وجود داشته ولی از لحاظ آماری این اختلاف قابل توجه یا معنیدار نیست.
مثال ۲: آنالیز واریانس دو طرفه در اکسل با اثرات متقابل
در مثال قبلی، اثر متقابل معنیدار نبود. در نتیجه، تفسیر تأثیرات اصلی یک مسئله ساده محسوب میشود که با آنالیز واریانس یک طرفه بسیار شباهت دارد. ولی سوال اینجاست که چگونه اثرات متقابل را میتوان درک یا نمایش داد؟ برای تأکید بر چگونگی عملکرد اثرات متقابل، از یک مثال ساده استفاده میکنیم تا شهود و درک آن سادهتر باشد.
تصور کنید که ما در حال انجام تست چشایی هستیم و متغیر وابسته میزان لذت یا رضایت از طعم است. دو عامل در این مثال به صورت متغیر نوع غذا (ستون Food) و نوع چاشنی یا سس (با نام ستونهای «سس خردل» Mustard و «سس شکلاتی» Chocolate Sauce) مشخص شده است. متغیر وابسته نیز امتیازی یا مقداری عددی است که هر فرد به ترکیب غذا و سس در ستونهای Mustard و Chocolate Sauce داده است.
به این ترتیب با استفاده از آنالیز واریانس دو طرفه در اکسل میخواهیم تعیین کنیم که کدام چاشنی بیشترین لذت یا امتیاز را از نظر افراد دارد.
برای ساده نگه داشتن مسئله، ما فقط دو نوع غذا (بستنی و هات داگ) و دو چاشنی (سس شکلات و خردل) را در تجزیه و تحلیل خود قرار خواهیم داد.
نکته: میتوان به اثرات متقابل در این مثال به عنوان یک عبارت «بستگی دارد» نگاه کرد. به این ترتیب خوشمزگی غذا، به ترکیب نوع سس یا چاشنی و نوع غذا بستگی دارد.
اثرات متقابل نشان میدهد که متغیر یا عامل دیگری بر رابطه بین متغیر مستقل و وابسته تأثیر میگذارد. این نوع تأثیر مدل را پیچیدهتر میکند، اما اگر به طور دقیق دنیای واقعی را منعکس کند، دانستن نحوه تفسیر آن بسیار مهم است. به عنوان مثال، رابطه بین چاشنیها و لذت بردن احتمالاً به نوع غذا بستگی دارد.
برای مثال ۲، به منظور پیادهسازی اثرات متقابل در آنالیز واریانس دو طرفه در اکسل مراحل زیر را انجام دهید.
- بر روی Analysis Data در برگه Data کلیک کنید.
- از پنجره Analysis Data گزینه Anova: Two-Factor With Replication را انتخاب کنید.
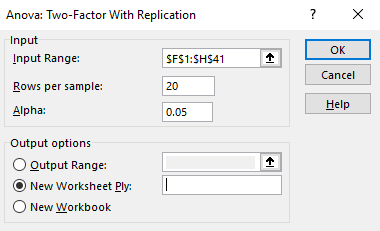
- در بخش Input، ناحیه مربوط به Input Range را با همه ستونهای داده F تا H مشخص کنید.
- در قسمت Rows per sample، عدد 20 را وارد کنید. این تعداد مشاهدات در هر گروه را نشان میدهد. به این ترتیب مشخص میکنیم که هر ۲۰ سطر مربوط به یک گروه است.
- همانطور که میدانید مقدار آلفای یا احتمال خطای نوع اول به صورت پیش فرض برابر با 0٫05 است. اگر میخواهید آزمون را سطح خطای کمتری اجرا کنید، مقدار مناسب را در کادر Alpha وارد کنید. ولی توجه داشته باشید که در این صورت برای کاهش خطای نوع دوم باید اندازه نمونه بزرگتری به کار ببرید.
- دکمه OK را کلیک کنید.
برای این مثال، باید پنجره پارامترهای این دستور، مطابق با تصویر 6 تنظیم شده باشد. البته توجه دارید که این گزینهها بسیار به مثال ۱ شبیه است، ولی از آنجا که اثرات متقابل هر دو عامل روی متغیر وابسته وجود دارد، تفسیر نتایج متفاوت خواهد بود.
به محض اجرای فرمان، یک کاربرگ جدید ایجاد شده و خروجی در آن طبق دو جدول مجزا، ثبت میشود. در جدولی که در بخش اول دیده میشود، همان خصوصیات مربوط به آمار توصیفی برای هر یک از عاملها محاسبه و نمایش داده میشود. اگر به سطر Average دقت کنید، متوجه خواهید شد که میانگین میزان رضایت از مزه برای هر یک از ترکیبهای مربوط به نوع غذا و چاشنی، با یکدیگر تفاوت دارند ولی باید از دید آماری نیز این تفاوت، به بوته آزمایش گذاشته شده و مورد بررسی قرار گیرد تا مشخص شود که این اختلاف ناشی از نمونهگیری نبوده و واقعا در جامعه نیز چنین تفاوتی وجود دارد.
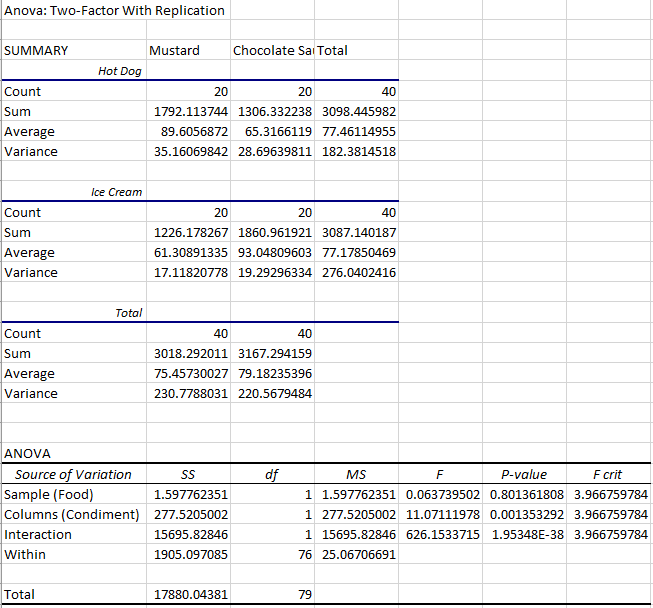
برای بررسی آزمون آماری کافی است که مقدار احتمال (P-value) در جدول دوم یا همان جدول ANOVA را با مقدار خطای ۰٫۰۵ مقایسه کنیم. برای سطر (Sample (Food، مقدار برابر با ۰٫۸۰۱۳ است که نشان از بیاثر بودن آن روی میزان رضایت از غذا دارد به این ترتیب بین نوع غذا و رضایت، ارتباطی وجود ندارد. پس مشخص است که همه بستنی و هات داگ را به یک میزان دوست دارند.
از آنجایی که مقدار احتمال برای سطر Columns برابر با ۰٫۰۰۱۳۵۳ است، میتوان نتیجه گرفت که میزان رضایت از مزه با توجه به نوع سس تفاوت دارد، بعضی به شکلات و بعضی به سس خردل تمایل دارند. پس چاشنیها از نظر افراد با یکدیگر تفاوت دارند. تا اینجا اثرات اصلی را بررسی کردیم و متوجه شدیم که اثر نوع غذا بر رضایت تاثیرگذار نیست ولی چاشنی در میانگین رضایت تاثیر گذار است.
این بار به سراغ اثر متقابل بین چاشنی و نوع غذا میرویم و به سطر Interaction، توجه کرده و P-value را تفسیر میکنیم. از آنجایی که مقدار احتمال برای این سطر برابر با 1.95348E-38 است و بسیار به صفر نزدیک محسوب میشود، نشان از اثر متقابل بین نوع غذا و چاشنی دارد. پس فرض صفر که برابری میانگین در ترکیب چاشنی و غذا را نشان میداد، رد شده و دلیل کافی برای وجود اثرات متقابل را در اختیارمان قرار میدهد.
به طور کلی، اثرات متقابل نشان میدهد که رابطه بین یک متغیر مستقل و یک متغیر وابسته بر اساس مقدار یک متغیر دیگر تغییر کرده و تحت تاثیر قرار میگیرد.
برای مدل آنالیز واریانس ارائه شده، تعامل و اثرات متقابل معنیدار، نشان میدهد که رابطه بین چاشنی و از طعم غذا بستگی به نوع غذا دارد. این ارتباط منطقی به نظر میرسد. ممکن است سس شکلات را خیلی دوست داشته باشید، اما خوردن آن را با هات داگ ترجیح نمیدهید و برعکس بستنی با سس خردل اصلا قابل خوردن نیست. پس انتخاب یا رضایت از هر یک از این چاشنیها بستگی به نوع غذا دارد.
نکته: اگر در جدول آنالیز واریانس، فقط اثرات اصلی معنیدار باشند، میتوانید اطمینان داشته باشید که سس شکلات یا خردل همیشه رضایت شما را بیشتر و به میزان ثابت بدون توجه به غذا افزایش میدهد. اما همانطور که مشخص است، این مورد با غذا و چاشنیهای به کار رفته در این مثال صدق نمیکند.
وقتی از نظر آماری، تأثیرات متقابل معنیدار و قابل توجه باشند، نمیتوان تأثیرات اصلی را به تنهایی تفسیر کرد. در مثال گفته شده، بدون دانستن نوع غذا نمیتوانید نوع چاشنی مورد پسند را مشخص کنید. گاهی خردل بهتر است در حالی که زمان دیگر سس شکلات مناسبتر در نظر گرفته میشود. همانطور که میبینید عبارت «بستگی دارد.» در اینجا لازم به نظر میرسد.
با استفاده از نمودارهای تخصصی که به عنوان نمودارهای اثرات متقابل شناخته میشوند، میتوان رابطه بین عاملها و متغیر وابسته را نشان داد. متأسفانه، اکسل نمیتواند این طرحها را به سادگی ایجاد کند. با این حال، میتوانید به کمک روشهای ترسیمی برای هر یک از گروهها نموداری رسم کرده و با مقایسه آنها وجود اثرات متقابل را مشخص کنید.
البته اثرات متقابل را با مشاهده مقدار میانگین گروهها نیز میتوان تشخیص داد. گروه «هات داگ/خردل» میانگینی برابر با 89٫6 و گروه «سس بستنی/شکلات» نیز میانگین برابر با 93٫0 دارد که هرکدام امتیازات رضایت نسبتاً بالایی دارند. برعکس، گروه «هاتداگ / سس شکلات» با میانگین 65٫3 و گروه «بستنی/خردل» با میانگین 61٫3 امتیاز کمتری داشته و اختلاف کمی نیز با یکدیگر دارند.
آنچه آنالیز واریانس دو طرفه در اکسل نشان نمیدهد
اگرچه تفسیر و نتایج حاصل از آنالیز واریانس دو طرفه در اکسل فوق العاده است، اما تمام ویژگیهایی را که یک بسته آماری کامل ارائه میدهد، ندارد. همانطور که اشاره کردیم، سادهترین راه برای درک تأثیرات تعامل استفاده از نمودارهای تعامل است. متأسفانه، اکسل نمیتواند آنها را ایجاد کند. همچنین اکسل فقط میتواند طرح های متعادل را تحلیل کند. اگر گروه های شما مشاهدات نابرابر دارند، باید از نرم افزارهای دیگر استفاده کنید.
از طرفی وقتی به وجود اختلاف یا تاثیرات اصلی یا متقابل پیبردیم، علاقمند هستیم، گروهی که باعث ایجاد این اختلاف میشود را نیز پیدا کنیم. این کار احتیاج به پسآزمونها (Pos-Hoc) یا آزمونهای تعقیبی دارد که اکسل از اجرای آنها عاجز است.
همچنین پیشفرضهایی لازم برای استفاده از آنالیز واریانس دو طرفه نیز در اکسل قابل اجرا نیست. به همین دلیل برای بررسی صحت مدل ارائه شده باید به نرمافزارها یا افزونههای دیگر اکسل مراجعه کنید. به این منظور بهتر است مطلب آنالیز واریانس یک طرفه در SPSS | راهنمای کاربردی را هم مطالعه کنید.
خلاصه و جمعبندی
همانطور که در این متن خواندید، آنالیز واریانس دو طرفه در اکسل توسط ابزارهای آماری آن، قابل اجرا است. البته محدودیتهایی نظیر آزمونهای برابری واریانس و تست نرمالیتی در اکسل وجود دارد که از نرمافزارهای دیگر محاسبات آماری برای انجام آنها میتوان استفاده کرد. ولی به هر حال انجام آزمون یا تکنیک آنالیز واریانس دو طرفه در اکسل به سادگی صورت گرفته و نتایج حاصل از آن در خروجی به راحتی قابل تفسیر و توصیف هستند. همین ویژگی طرفداران ابزارهای آماری اکسل را افزوده است. البته افزونههای دیگری نیز برای انجام روشهای مختلف آماری در اکسل وجود دارد که معمولا با صرف هزینه میتوانید آنها را خریداری کرده و به کار ببرید. در حالیکه افزونه معرفی شده (Analysis Toolpak) رایگان بوده بسیاری از نیازهای کاربران را برآورده میسازد.