تحلیل تنش و تغییر شکل در تیرها — بخش اول: محاسبه تنش برشی و خمشی

تحلیل تنش و تغییر شکل موجود در تیرها، یکی از مباحث مهم و کاربردی در مقاومت مصالح محسوب میشود؛ چراکه بسیاری از سازهها را میتوان به صورت یک تیر مستقیم یا مجموعهای از تیرهای مستقیم در نظر گرفت. در این مقاله، به مباحثی از قبیل تحلیل نیروی برشی و گشتاور خمشی، رسم نمودار برش-خمش و محاسبه تنش برشی و خمشی در تیرها خواهیم پرداخت. شما میتوانید با مشاهده فیلمهای مجموعه آموزش مقاومت مصالح – درس، تمرین، حل مثال و تست در فرادرس، اصول تحلیل تنش و تغییر شکل در تیرها و دیگر مفاهیم مبتدی تا پیشرفته مرتبط با مقاومت مصالح را به راحتی و حل مثالهای متعدد یاد بگیرد.
نیروی برشی و گشتاور خمشی در تیرها
برای تعیین نیروی برشی و گشتاور خمشی در طول یک تیر، ابتدا باید عکسالعملهای خارجی را در شرایط مرزی به دست آورد.
به عنوان مثال در شکل زیر، یک تیر یکسر گیردار تحت نیروی خارجی (قرمز) قرار گرفته است. اگر تیر در شرایط مرزیِ ثابت باشد، عکسالعملهای آن (آبی) به صورت زیر نمایش داده میشوند:
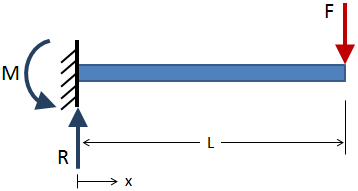
پس از محاسبه عکسالعملهای خارجی، باید چند مقطع را در طول تیر در نظر گرفت و عکسالعملهای خارجی در هر یک از آنها را نیز تعیین کرد. در شکل زیر، نمونهای از یک مقطع تیر نمایش داده شده است:

در محاسبه عکسالعملهای خارجی، تفاوتی بین انتخاب طرف راست یا چپ مقطع وجود ندارد و این موضوع تأثیری بر روی نتایج نخواهد گذاشت. بنابراین، پیشنهاد میکنیم بخشی را انتخاب کنید که محاسبات در آن برایتان راحتتر است. در شکل بالا، ما سمت راست مقطع برای انجام محاسبات انتخاب کردیم. عکسالعملهای موجود در این مقطع، با پیکانهای آبی مشخص شدهاند.
قواعد علامتگذاری
تعیین علامت نیروهای برشی و گشتاورها، اهمیت بالایی در انجام محاسبات دارد. تعیین علامت، پس از در نظر گرفتن یک مقطع و محاسبه عکسالعملهای موجود در آن نسبت به بخش دیگر تیر انجام میشود. در صورتی که جهت نیروی برشی در مقطع به صورت ساعتگرد باشد، علامت آن مثبت و اگر پادساعتگرد باشد، علامت آن منفی خواهد بود. اگر گشتاور چرخشی به بخش بالایی تیر فشار وارد کند و بخش پایینی را تحت کشش قرار دهد (باعث لبخند تیر شود)، علامت آن مثبت در نظر گرفته میشود.
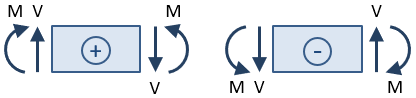
بر اساس این قواعد، علامت نیروی برشی در مقطع تصویر بالا، به دلیل ساعتگرد بودن مثبت خواهد بود. به علاوه، از آنجایی که گشتاور به بخش پایینی تیر فشار وارد میکند و بخش بالایی را تحت فشار قرار میدهد (باعث اخم تیر میشود)، علامت آن منفی در نظر گرفته میشود. شکل زیر، قواعد علامتگذاری نیروی برشی و گشتاور خمشی درون تیرها را نشان میدهد.
رسم نمودار نیروی برشی و گشتاور خمشی برای تیرها
وضعیت نیروهای برشی و گشتاورهای خمشی درون تیرها عموماً با استفاده از رسم نمودار بیان میشود. «نمودار نیروی برشی» (Shear Force Diagram)، نیروی برشی اعمال شده در امتداد تیر و «نمودار گشتاور خمشی» (Bending Moment Diagram)، گشتاور خمشی در طول تیر را نشان میدهد. با ترکیب این دو نمودار، نمودار برش- خمش به وجود میآید. شکل زیر، نمونهای از یک نمودار برش-خمش را نشان میدهد:
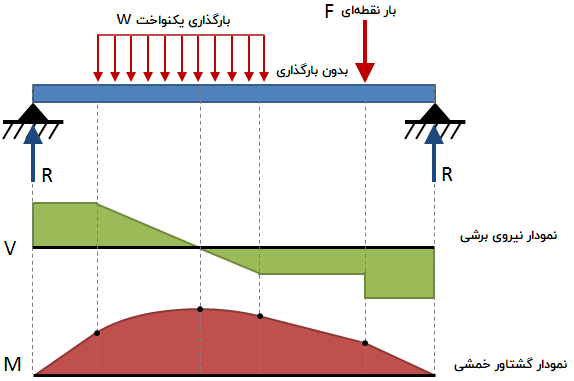
قوانین کلی رسم نمودار برش-خمش در جدول زیر آورده شده است:
| نمودار نیروی برشی | نمودار گشتاور خمشی |
| بارهای نقطهای یا متمرکز، باعث یک جهش در روند تغییرات نمودار میشوند. مثبت یا منفی بودن این جهش به علامت بار نقطهای بستگی دارد. | نمودار گشتاور خمشی برای بخشهای بدون بارگذاری تیر، به صورت یک خط راست و شیبدار است. شیب این خط با مقدار نیروی برشی برابری میکند. |
| شکل نمودار در بارگذاریهای یکنواخت به صورت یک خط مستقیم و شیبدار است. شیب این خط با مقدار بار توزیع شده برابری میکند. | وجود بارگذاریهای یکنواخت در تیر، به صورت یک منحنی سهمیوار در نمودار گشتاور خمشی نمایش داده میشود. |
| نواحی بدون بارگذاری در راستای تیر، به وسیله خطوط افقی در نمودار نمایش داده میشوند | مقادیر ماکسیمم/مینیمم گشتاور در هنگام تقاطع نمودار نیروی برشی با نقطه صفر رخ میدهند. |
|
میزان نیروی برشی در هر نقطه از تیر با شیب گشتاور در هر همان نقطه برابر است:
$$V = {dM \over dx}$$ |
گشتاور در هر نقطه از تیر با سطح زیر نمودار نیروی برشی تا نقطه برابر است:
$$M=\int{V dx}$$ |
تنش خمشی در تیرها
مقدار گشتاور خمشی (M) در طول یک تیر از طریق رسم نمودار گشتاور خمشی قابل محاسبه است. مقادیر به دست آمده از این نمودار را میتوان برای تعیین تنش خمشی در هر مقطع دلخواه به کار برد.
بر اساس «رابطه خمش» (Flexure Formula)، مقدار گشتاور خمشی در ارتفاع سطح مقطع تیر تغییر میکند.
$$\sigma_{b} = - {My \over I_c}$$
M: گشتاور خمشی در محل مورد نظر بر روی تیر؛ Ic: گشتاور دوم سطح حول محور خنثی در سطح مقطع تیر؛ y: فاصله عمودی محور خنثی تیر تا نقطه مورد نظر؛ علامت منفی در رابطه بالا، بیانگر این است که اعمال گشتاور مثبت باعث ایجاد تنش فشاری در بالای محور خنثی تیر خواهد شد.
تنش خمشی در محور خنثی تیر برابر با صفر است. این محور بر روی مرکز ثقل هندسی تیر قرار دارد. با دور شدن از محور خنثی، مقدار تنش خمشی درون تیر به صورت خطی افزایش مییابد. بیشترین مقدار این تنش در بالاییترین و پایینیترین بخش تیر مشاهده میشود.

مقدار تنش خمشی ماکسیمم از رابطه زیر به دست میآید:
$$\sigma_{b.max} = {Mc \over I_c}$$
در رابطه بالا، c، فاصله عمودی مرکز هندسی سطح مقطع تیر تا بالاییترین/پایینیترین بخش آن است.
اگر هندسه تیر در نزدیکی محور خنثی به صورت نامتقارن باشد، فاصله محور خنثی تا بالا و پایین تیر یکسان نخواهد بود (شکل زیر). به علاوه، تنش ماکسیمم در دورترین فاصله از این محور رخ خواهد داد. در شکل زیر، مقدار تنش کششی در بالای تیر از تنش فشاری در پایین آن بزرگتر است.
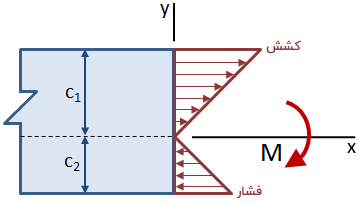
یکی از کمیتهای کاربردی در محاسبه تنشهای خمشی، «مدول مقطع» (Section Modulus) است. این کمیت، گشتاور دوم سطح حول محور خنثی (Ic) و فاصله عمودی مرکز هندسی سطح مقطع تیر تا بالاییترین/پایینیترین بخش آن (c) را با هم ادغام میکند.
$$S = {I_c \over c}$$
مزیت مدول مقطع این است که میتوان به وسیله آن، خصوصیات مقاومت خمشی یک مقطع را در یک عبارت بیان کرد. با جایگذاری مدول مقطع در رابطه خمش، امکان محاسبه تنش خمشی ماکسیمم در مقطع مورد نظر فراهم میشود:
$$\sigma_{b.max} = {M \over S}$$
تنش برشی در تیرها
میزان نیروی برشی (V) در راستای طول تیر را میتوان از طریق نمودار نیروی برشی به دست آورد و از آن برای محاسبه تنش برشی بر روی سطح مقطع تیر در محل مورد نظر استفاده کرد. میانگین تنش برشی بر روی سطح مقطع، با استفاده از رابطه زیر تعیین میشود:
$$\tau_{avg} = {V \over A}$$
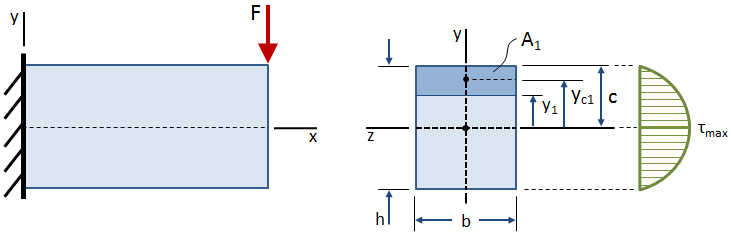
مقدار تنش برشی در سطوح آزاد (بالا و پایین تیر) صفر است و در مرکز هندسی مقطع بیشترین مقدار را دارد.
تنش برشی در نقطهای با فاصله y1 از مرکز هندسی مقطع با استفاده از معادله زیر به دست میآید:
$$\tau = {VQ \over I_c b}$$
V: نیروی برش اعمال شده بر محل سطح مقطع؛ Ic: گشتاور دوم سطح حول محور خنثی در سطح مقطع؛ b: عرض سطح مقطع؛ تمام این عبارتها ثابت هستند اما Q، گشتاور اول سطح در محدوده نقطه مورد بررسی و سطح آزاد مقطع است که از رابطه زیر به دست میآید:
$$Q = \int_{y1}^{c} {y ~ dA}$$
در ادامه، نحوه محاسبه تنش برشی در چند مقطع متداول را توضیح خواهیم داد.
محاسبه تنش برشی در مقاطع مستطیلی
نحوه توزیع تنش برشی در ارتفاع یک مقطع مستطیلی در شکل زیر نمایش داده شده است:
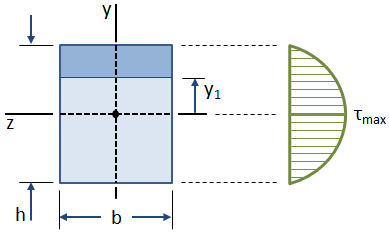
گشتاور اول سطح در هر نقطه دلخواه با فاصله عمودی y1 از مرکز هندسی مقطع با استفاده از رابطه زیر محاسبه میشود:
$$Q = {b \over 2} \left({h^2 \over 4} - y_1^2 \right)$$
حداکثر مقدار Q در محور خنثی تیر (y1=0) رخ میدهد:
$$Q_{max} = {b h^2 \over 8}$$
مقدار تنش برشی در هر نقطه دلخواه با فاصله عمودی y1 از مرکز هندسی مقطع نیز از رابطه زیر به دست میآید:
$$\tau = {VQ \over I_c b} = {V \over 2 I_c} \left({h^2 \over 4} - y_1^2 \right)$$
در معادله بالا، گشتاور دوم سطح حول محور خنثی در سطح مقطع (Ic) به صورت زیر تعیین میشود:
$$I_c = {b h^3 \over 12}$$
تنش برشی ماکسیمم، در محور خنثی تیر رخ میدهد و مقدار آن از رابطه زیر به دست میآید:
$$\tau_{max} = {3V \over 2A}$$
در معادله بالا، A=bh و مساحت سطح مقطع است. توجه داشته باشید که تنش برشی ماکسیمم در سطح مقطع، 50 درصد بیشتر از میانگین تنش (V/A) خواهد بود.
محاسبه تنش برشی در مقاطع دایرهای
در شکل زیر، یک مقطع دایرهای نمایش داده شده است:
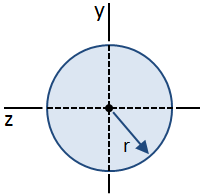
معادلات تنش برشی برای این حالت، با فرض ثابت بودن تنش برشی در امتداد عرض تیر به دست میآیند. این فرض، تنها در مرکز هندسی یک مقطع دایرهای صادق است. بنابراین، نمیتوان توزیع تنش برشی در امتداد طول مقطع آر به آسانی تعیین کرد. با این وجود، تنش برشی ماکسیمم (در مرکز هندسی) مقطع قابل محاسبه خواهد بود. حداکثر مقدار گشتاور اول سطح (Q) برای مقاطع دایرهای در مرکز هندسی آنها رخ میدهد و از طریق رابطه زیر به دست میآید:
$$Q_{max} = {2 r^3 \over 3}$$
تنش برشی ماکسیمم نیز به صورت زیر محاسبه میشود:
$$\tau_{max} = {V Q_{max} \over I_c b} = {4V \over 3A}$$
b=2r: قطر یا عرض سطح مقطع؛ A=πr2: مساحت سطح مقطع؛ Ic: گشتاور دوم سطح
$$I_c = {\pi r^4 \over 4}$$
محاسبه تنش برشی در مقاطع لولهای (گرد)
در شکل زیر، یک مقطع لولهای گرد را مشاهده میکنید:

حداکثر گشتاور اول سطح برای این مقطع برابر است با:
$$Q_{max} = {2 \over 3} \left(r_o^3 - r_i^3 \right)$$
تنش برشی ماکسیمم نیز به صورت زیر محاسبه میشود:
$$\tau_{max} = {V Q_{max} \over I_c b} = {4V \over 3A} \left({r_o^2 + r_o r_i + r_i^2 \over r_o^2 + r_i^2} \right)$$
در معادله بالا، داریم:
عرض مؤثر سطح مقطع
$$b = 2 (r_o - r_i)$$
گشتاور دوم سطح
$$I_c = {\pi \over 4} \left(r_o^4 - r_i^4 \right)$$
مساحت سطح مقطع
$$A = \pi (r_o^2 - r_i^2)$$
تنشهای برشی در تیر I شکل
در شکل زیر، توزیع تنش برشی در امتداد جانِ یک تیر I نشان داده شده است.
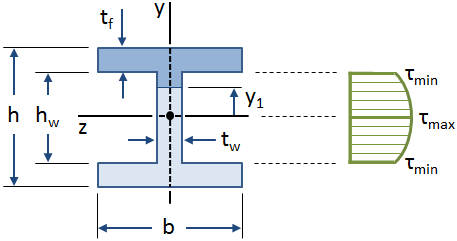
معادلات تنش برشی، با فرض ثابت بودن این تنش در امتداد عرضی تیر به دست میآیند. این فرض برای جانِ تیرهای I شکل صحیح است اما برای فلنجها (بخصوص در محل تقاطع جان و فلنج) اعتباری ندارد. حدود 90 تا 95 درصد از نیروی برشی کل در تیرهای I شکل به جان وارد میشود. از اینرو، در محاسبات محافظهکارانه میتوان فرض کرد که جان، تمام نیروی برشی را تحمل میکند.
گشتاور اول سطح برای جان یک تیر I شکل، به صورت به دست میآید:
$$Q = {b \over 8} (h^2 - h_w^2) + {t_w \over 8} (h_w^2 - 4 y_1^2)$$
رابطه زیر، برای محاسبه تنش برشی در امتداد جان تیر I شکل به کار میرود:
$$\tau = {VQ \over I_c t_w} = {V \over 8 I_c t_w} \left[b (h^2 - h_w^2) + t_w (h_w^2 - 4 y_1^2) \right]$$
tw، ضخامت جان تیر و Ic، ممان اینرسی مرکز سطح تیر است که از معادله زیر به دست میآید:
$$I_c = {bh^3 \over 12} - {(b - t_w) h_w^3 \over 12} = {1 \over 12} (bh^3 - b h_w^3 + t_w h_w^3)$$
مقدار ماکسیمم تنش برشی در محور خنثی (y1=0) و مقدار مینیمم تنش برشی در محل تقاطع الیاف بیرونی جان تیر با فلنجها (2/hw±) ظاهر میشود:
$$\tau_{max} = {V \over 8 I_c t_w} (bh^2 - b h_w^2 + t_w h_w^2)$$
$$\tau_{min} = {Vb \over 8 I_c t_w} (h^2 - h_w^2)$$
در بخش دوم این مقاله، فهرستی از معادلات مرتبط با خمیدگی، شیب، برش و گشتاور موجود در امتداد تیرهای مستقیم برای شرایط مرزی و بارگذاری متفاوت ارائه خواهد شد که اکثر حالتهای متداول را پوشش میدهد.











سلام
ی سوال داشتم اگ بتونی حلش کنید استاد
اگ ی میله یک متری تیر اهن ipe 200 داشت باشیم و از ی سر جوش و سر دیگر 60000نیوتن بش نیرو وارد کنید و hبرابردو دهم و b ان برابر یک دهم باشد و eیا همان مدول الاسیتیسیته ان 200’گیگا پاسکال باشه میله ما چقدر خم میسه
با سلام و خسته نباشید. می خواستم بدونم در فرایند طراحی و شبیه سازی چطور باید حداکثر تنش و یا کرنش یا مقاومت یک ماده را بدست بیاوریم؟
سلام برای مقاطی مثلث هم میشه فرمولشو بگین و مقدار ماکزیمم را نشان بدهید
اگه یه مقطع ای تار خنثی در وسط نباشه ایا بازم هم تنش برشی در وسط حداکثر هست؟
با سلام و وقت بخیر
احسنت ، عالی بود.
سلام. خیلی خوب و عالی بود.
قالب سایت هم خیلی خوبه.
واقعا دستتون درد نکنه ❤
سلام فرمول ۱۶T/πd^3 برای چ مواردی استفاده میشه و مربوط به چه تنشی هست
و فرمول 32M/πd^3 واسه چیه و کجا استفاده میشه
با سلام؛
رابطه اول، تنش برشی ماکزیمم و رابطه دوم، تنش ماکزیمم در مقاطع دایرهای شکل است. برای آشنایی بیشتر راجع به این فرمولها، مطالعه مطلب «پیچش و تنش برشی — به زبان ساده» را به شما پیشنهاد میکنیم.
از همراهیتان با مجله فرادرس سپاسگزاریم.
سلام ، میشه برای سطح مقطع لوزی هم فرمولش را بگید و مقدار ماکزیمم را نشان دهید