فاصله اطمینان و تفسیر آن — راهنمای کاربردی SPSS

مبحث برآوردیابی در تحلیل‌های آماری به دو بخش «برآورد نقطه‌ای» (Point Estimation) و «برآورد فاصله‌ای» (Interval Estimation) تقسیم می‌شود. در واقع برآورد فاصله‌ای همان «فاصله اطمینان» (Confidence Interval) است که براساس آن حتی می‌توان یک آزمون آماری نیز برای پارامتر جامعه انجام داد. در این نوشتار به بررسی فاصله اطمینان و تفسیر آن می‌پردازیم، زیرا در بسیاری از مسائل و تجزیه و تحلیل‌های آماری با این مفهوم سر و کار داریم. پس بهتر است که از آن به درستی استفاده کنیم.

برای آشنایی بیشتر با نحوه محاسبه فاصله اطمینان بهتر است مطلب فاصله اطمینان (Confidence Interval) — به زبان ساده و آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن نوشتارهای مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری و آزمون های فرض آماری در یادگیری ماشین — اصول و مفاهیم اولیه نیز خالی از لطف نیست.

فاصله اطمینان و تفسیر آن

فاصله اطمینان و تفسیر آن به شکل تاثیرگذاری در تجزیه و تحلیل آماری بخصوص در زمینه برآوردیابی نقش ایفا می‌کند. متاسفانه گاهی بعضی از کاربران تکنیک‌های آماری، تفسیر نادرستی از فاصله اطمینان ارائه می‌دهند. بنابراین در این نوشتار سعی داریم که با مفهوم فاصله اطمینان بیشتر آشنا شده تا قادر به توصیف بهتر آن باشیم. به یاد داشته باشید که منظور از پارامتر جامعه، مقداری نامشخص ولی ثابت است که براساس نمونه تصادفی قصد برآورد آن را داریم. از طرفی از آنجایی که در هر بار نمونه‌گیری ممکن است مشاهدات مختلفی را از جامعه آماری جمع‌آوری کنیم، با یک فرآیند تصادفی مواجه هستیم. همانطور که می‌دانید احتمال یک روش برای بیان و توصیف رفتار پدیده‌های تصادفی است. در ادامه قصد داریم با معرفی فاصله اطمینان و تفسیر آن به شکلی برخورد کنیم که این مفاهیم در آن در نظر گرفته شود.

فیلم آموزش مبانی و روش های اقتصاد سنجی با ایویوز Eviews در فرادرس

کلیک کنید

یک آزمون فرض آماری از دو فرضیه به نام‌های «فرض صفر» (Null Hypothesis) و «فرض مقابل» (Alternative Hypothesis) تشکیل شده که به صورت یک گزاره در مورد پارامتر جامعه یا توزیع آن بیان می‌شوند. هدف از انجام آزمون «فرض آماری» (Statistical Hypothesis Testing) مشخص کردن یک تصمیم است که منجر به رد فرض صفر می‌شود. شاید بتوان رد فرض صفر را تایید فرض مقابل در نظر بگیریم. در صورتی که دلایلی کافی توسط نمونه برای رد فرض صفر وجود نداشته باشد، می‌گوییم دلیلی برای رد فرض صفر توسط نمونه تصادفی نداریم. این تصمیمات و نتایج گرفته شده از آزمون فرض آماری همراه با یک خطای قابل تحمل به نام احتمال خطای نوع اول (Error Type I) که از قبل مشخص شده، صورت می‌گیرد که اغلب آن را با $$\alpha$$ نشان می‌دهیم و گاهی به آن «سطح آزمون» (Test Level) نیز می‌گوییم.

ولی در مقابل فاصله اطمینان، ناحیه‌ای تصادفی را ایجاد می‌کند که بواسطه آن می‌توانیم نسبت به پوشش پارامتر مجهول جامعه در این فاصله به میزان دلخواه $$1-\alpha$$ اطمینان داشته باشیم. منظور از ناحیه‌ تصادفی، فاصله‌ای است که براساس یک نمونه مثلا $$n$$ تایی تولید شده. واضح است که اگر از نمونه‌ $$n$$‌ تایی دیگر استفاده شود، این فاصله متفاوت خواهد بود. بنابراین پدیده تصادفی در اینجا یک فاصله اطمینان تصادفی با میزان یا سطح اطمینان مشخص ایجاد می‌کند. در اینجا $$1-\alpha$$ را «سطح اطمینان» (Confidence Level) می‌گویند.

برای مثال ممکن است بگویم که یک فاصله اطمینان ۹۵٪ برای میانگین جامعه به صورت زیر است:

$$\large (150, 158)$$

مقدار ۱۵۰ را کران پایین و ۱۵۸ را کران بالای این فاصله اطمینان می‌نامند. گاهی به اشتباه این فاصله اطمینان را فاصله‌ای می‌نامند که پارامتر جامعه به احتمال ۹۵٪ در آن قرار می‌گیرد. با این تعریف به نظر می‌رسد که پارامتر جامعه یک پدیده یا متغیر تصادفی است که برای آن احتمال محاسبه شده است. در حالیکه می‌دانیم پدیده تصادفی در اینجا مقدارهای حاصل از نمونه‌گیری و نمونه‌ها است. بنابراین باید گفت که این فاصله به احتمال ۹۵٪ شامل پارامتر جامعه است. به بیان دیگر این عبارت نشان می‌دهد که با استفاده از ۱۰۰ بار نمونه‌گیری و تولید فاصله اطمینان‌های مرتبط، می‌توان مطمئن بود که ۹۵ فاصله اطمینان که البته فاصله ذکر شده نیز یکی از آن‌ها است، پارامتر جامعه را پوشش می‌دهند، یعنی ۹۵ فاصله اطمینان از ۱۰۰ فاصله تولید شده، شامل پارامتر جامعه هستند. مشخص است که در این حالت طول این فاصله اطمینان برابر است با؛

$$158-150=8$$

نکته: فاصله اطمینان می‌تواند به صورت تک متغیر، دو متغیره و چند متغیره برای پارامتر‌های جامعه آماری به کار رود. به این ترتیب ممکن است برای میانگین و واریانس جامعه آماری یک فاصله اطمینان دو بعدی ایجاد کنیم.

طول فاصله اطمینان

یکی از ویژگی‌های جالب در این بحث، «طول فاصله اطمینان» (Confidence Interval Width) است. طول فاصله اطمینان، میزان اختلاف بین کران پایین و بالای فاصله اطمینان را بیان می‌کند. به این ترتیب می‌توان طول فاصله اطمینان را تابعی از «سطح اطمینان» (Confidence Level) و «خطای نمونه‌گیری» (Sampling Error) در نظر گرفت. به نظر می‌رسد که طول فاصله اطمینان می‌تواند معیاری برای دقت برآوردگر فاصله نیز محسوب شود. به این ترتیب هر چه سطح اطمینان افزایش یابد، طول فاصله اطمینان نیز افزایش خواهد داشت و اگر سطح اطمینان را کاهش دهیم، طول فاصله اطمینان کاهش یافته و بسته به نوع دقت برآوردگر فاصله بیشتر می‌شود. پس از آنجایی که کم شدن طول فاصله اطمینان، دقت برآوردگر فاصله‌ای را زیاد می‌کند، برای افزایش دقت برآوردگر فاصله در سطح اطمینان ثابت باید اندازه نمونه را افزایش داده تا خطای نمونه‌گیری کاهش یابد. به بیان دیگر اگر سطح اطمینان را ثابت در نظر بگیریم، برای افزایش میزان دقت یا کاهش طول فاصله اطمینان در برآورد فاصله‌ای، باید خطای نمونه‌گیری را کاهش داد. بنابراین بهتر است با خطای نمونه‌گیری بیشتر آشنا شویم.

خطای نمونه‌گیری

زمانی که امکان بررسی همه اعضای جامعه آماری میسر نباشد، دست به نمونه‌گیری می‌زنیم. مشخص است که در نمونه حاصل، سعی بر این است که خصوصیات جامعه آماری لحاظ شود ولی متاسفانه از آنجایی که بعضی از اعضای جامعه آماری در نمونه نقش ندارند، ممکن است در برآورد و قضاوت در مورد پارامتر جامعه دچار خطا شویم. میزان خطا یا دقت برآورد از یک نمونه به نمونه‌ دیگر متفاوت است.

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

برای مثال فرض کنید، می‌خواهیم درصد افرادی که یک برنامه تلویزیونی را مشاهده می‌کنند، برآورد کنیم. برای این کار از ۴۰ خانواده که بطور تصادفی انتخاب شده‌اند، استفاده کرده‌ایم. ممکن است همه این خانواده‌ها برنامه مورد نظر را از تلویزیون مشاهده کنند در این صورت برآورد پارامتر ما برابر ۱۰۰٪ است ولی ممکن است در یک نمونه دیگر ۴۰ خانواری که تهیه کرده‌ایم، این درصد برابر با ۵۰٪ باشد. به این ترتیب مشخص می‌شود که بواسطه نمونه‌گیری ممکن است در مورد تخمین پارامتر جامعه دچار خطا شویم.

خطای نمونه‌گیری همین تغییرات در برآورد پارامتر جامعه را نشان می‌دهد. زمانی که نمونه تصادفی با جامعه آماری تفاوت زیادی در مقدارها و خصوصیات داشته باشد، میزان خطای برآورد پارامتر جامعه، بزرگ می‌شود. بنابراین برای کاهش میزان خطای برآورد باید نمونه‌هایی با حجم بیشتر و به شکل تصادفی تهیه کرد تا نتایج تحلیل‌ها و برآوردها بخصوص برآوردهای فاصله‌ای، دقیق‌تر و قابل اعتمادتر شوند.

نکته: واضح است که اگر بخواهیم خطای نمونه‌گیری را به صفر کاهش یا دقت برآورد برآورد فاصله‌ای را به ۱۰۰٪ افزایش دهیم، باید حجم نمونه را برابر با اندازه جامعه آماری انتخاب کنیم. گاهی برای افزایش دقت یا کاهش واریانس برآوردگرها از روش‌های بازنمونه‌گیری مانند روش بوت‌استرپ (Bootstrapping) استفاده می‌شود.

فاصله اطمینان میانگین و تفسیر آن

در تصویر زیر یک جدول از یک تحلیل یا آزمون آماری برای مقایسه میانگین درآمد در بین دو گروه خانم‌ها و آقایان که بوسیله متغیر Gender مشخص شده‌اند را مشاهده می‌کنید. آیا می‌توان نتیجه گرفت که میانگین درآمد خانم‌ها (Female) کمتر از میانگین درآمد آقایان (Male) است؟ این نتایج براساس یک نمونه 1698 تایی از دو گروه خانم‌ها به تعداد $$N=838$$ و آقایان $$N=860$$ تهیه شده است. همانطور که دیده می‌شود فراوانی‌ها در بین این دو گروه یکسان نیست. از طرفی تفاوت در توزیع و پراکندگی این داده‌ها برای دو گروه خانم‌ها و آقایان نیز وجود دارد. میانگین درآمد برای گروه خانم‌ها و آقایان به ترتیب $$Mean = 39341$$ و $$Mean=46640$$ است. آیا این اختلاف واقعا در جامعه آماری نیز وجود دارد یا تفاوت به علت خطای نمونه‌گیری و وجود نمونه‌های متفاوت است.

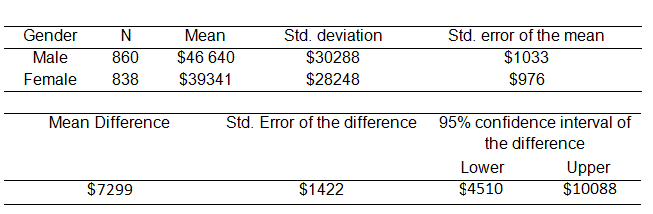
برای مثال در گروه آقایان، میزان پراکندگی یا انحراف استاندارد برای حقوق دریافتی حدود 30288 دلار است در حالیکه درآمد خانم‌ها، پراکندگی کمتری دارد و انحراف معیار آن برابر با 28248 دلار است. اگر بخواهیم میزان انحراف میانگین درآمد را برای هر دو گروه مقایسه کنیم، بطوری که هر دو گروه دارای تعداد اعضای یکسانی باشند یا تعداد اعضای گروه‌ها در میزان انحراف دخیل نباشد، کافی است که انحراف معیار را بر جذر تعداد اعضای دو گروه تقسیم کنیم. این کار منجر به محاسبه «خطای استاندارد میانگین» (Standard Error of the Mean) می‌شود. در این صورت اگر انحراف استاندارد را با $$\sigma$$ و تعداد اعضای هر گروه را با $$n$$‌ نشان دهیم، خطای استاندارد میانگین یا به اختصار خطای میانگین که با نماد $$SE$$ نشان داده می‌شود، به صورت زیر محاسبه خواهد شد.

$$\large SE=\dfrac{\sigma}{\sqrt{n}}$$

بنابراین نمونه‌های مختلفی می‌توان تهیه و بوسیله میانگین آن‌ها، پارامتر جامعه آماری را برآورد کرد. ولی هدف از محاسبه خطای استاندارد میانگین، بدست آوردن واریانس یا متوسط تغییرات این برآوردگرها است. می‌توان نشان داد که واریانس مربوط به برآوردگرها (میانگین نمونه‌ها) به مانند رابطه قبلی به صورت زیر بدست می‌آید.

$$\large \sigma^2_{mean}=\dfrac{\sigma^2}{n}$$

که در آن $$\sigma$$ انحراف معیار جامعه آماری است. البته می‌توان در صورتی که انحراف معیار جامعه معلوم نباشد از برآورد آن یعنی $$s$$‌ استفاده کرد. در نتیجه برآوردها به صورت مجانبی خواهند بود.

همانطور که گفته شد یکی از عوامل موثر در ساختار فاصله اطمینان خطای میانگین یا همان خطای نمونه‌گیری است. همانطور که در جدول تصویر بالا مشاهده می‌کنیم، اختلاف بین میانگین درآمد آقایان و خانم‌ها در ستون Mean Difference مشخص شده. همچنین خطای نمونه‌گیری برای میانگین اختلاف نیز برابر است با $$1422$$. به این ترتیب با استفاده فاصله اطمینان با سطح اطمینان ۹۵٪ برای میانگین اختلافات درآمد در بین دو گروه، کران‌ها به صورت زیر در خواهد آمد.

$$\large (4510 , 10088)$$

منظور از این فاصله آن است که ۹۵ درصد فاصله‌های اطمینان به این شکل، شامل پارامتر مجهول یعنی میانگین اختلاف درآمدی در بین دو گروه خانم‌ها و آقایان است.

نکته: از آنجایی که این کران‌های این فاصله اطمینان مثبت هستند، می‌توان گفت که به طور متوسط، درآمد آقایان بیشتر از خانم‌ها است.

محاسبه فاصله اطمینان برای پارامتر اختلاف میانگین دو جامعه

فرض کنید می‌خواهیم اطلاعاتی که در جدول ۱ وجود دارد را در SPSS وارد کنیم تا فاصله اطمینان و آزمون آماری را برای میانگین اختلافات انجام دهیم. برای انجام این کار از نسخه 25 نرم‌افزار SPSS استفاده می‌کنیم.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

به این ترتیب طبق مسیر زیر اقدام می‌کنیم.

Analyze -> Compare Means -> Summary Independent-Samples T Test

با اجرای این دستور پنجره‌ای به مانند شکل زیر ظاهر شده که کافی است پارامترهای آن را مطابق تصویر تعیین کنیم.

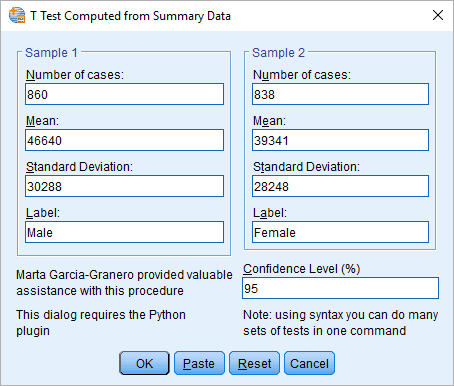
البته اگر می‌خواهید از محیط Syntax استفاده کنید باید کد دستوری زیر را وارد کنید.

1DATASET ACTIVATE orig.
2SPSSINC SUMMARY TTEST N1=860 MEAN1=46640 SD1=30288 LABEL1="Male" N2=838 MEAN2=39341 SD2=28248 
3    LABEL2="Female" CI=95.

نکته: برای اجرای این دستور، احتیاج به افزونه اجرای برنامه‌های پایتون در محیط SPSS به نام Python Plugins‌ دارید. برای اطلاعات بیشتر در  این زمینه، بهتر است مطلب پایتون در SPSS — راهنمای گام به گام  و انجام عملیات تکراری با پایتون در SPSS — راهنمای گام به گام را مطالعه کنید.

با انتخاب دکمه OK، محاسبات انجام شده و نتیجه به شکل تصویر زیر دیده می‌شود.

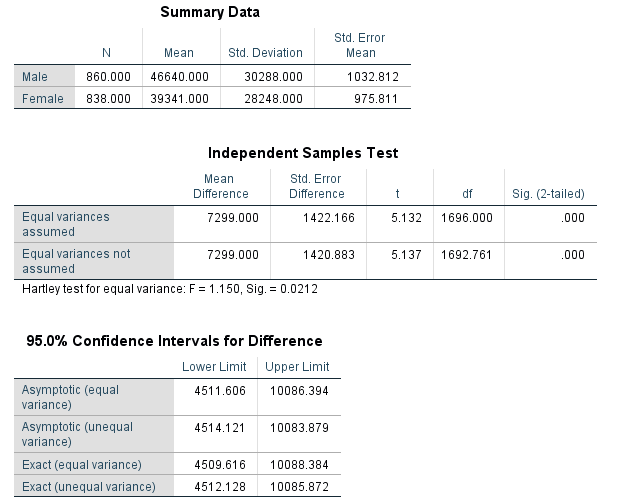
ابتدا جدولی برای نمایش خصوصیات داده‌ها به صورت یک جدول آمار توصیفی (Summary Data) ارائه شده است. ستون‌ها شامل مقدارهای تعداد (N)، میانگین (Mean)، انحراف استاندارد (Std Deviation) و خطای میانگین (Std. Error Mean) خواهند بود.

کاملا مشخص است که نرم‌افزار SPSS دو حالت برای انجام آزمون آماری در جدول Independent Samples Test در نظر گرفته است. حالت اول در سطر اول یعنی Equal variances assumed، با فرض مساوی بودن انحراف معیار یا واریانس در بین هر دو گروه انجام شده و آماره آزمون و فاصله اطمینان برای این حالت محاسبه شده است. ولی در سطر یا بخش دوم جدول‌ با فرض نامساوی بودن واریانس‌ها یعنی Equal variances not assumed همان محاسبات انجام شده است. اما از آنجایی که به نظر می‌رسد بین انحراف معیار یا خطای میانگین در هر دو حالت اختلاف زیادی وجود ندارد، می‌توان یکسان بودن واریانس‌ها را نتیجه گرفت.

در انتها نیز فاصله اطمینان ۹۵٪ درصدی برای اختلاف میانگین دو گروه ظاهر شده است. البته باز هم خروجی‌ها با توجه به فرض برابری یا نابرابری واریانس‌ها تفکیک شده است. همچنین برای محاسبه فاصله اطمینان از توزیع واقعی آماره آزمون (Exact) و مجانبی (Asymptotic) استفاده شده است.

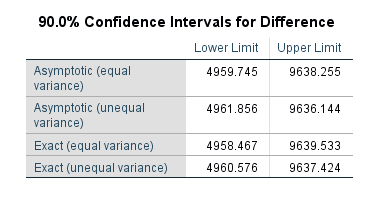
به نظر می‌رسد که طول فاصله اطمینان در اینجا تقریبا برابر با 5578 دلار است. حال فرض کنید که مقدار اطمینان را از ۹۵٪ به ۹۰٪ تغییر دهیم. با اجرای این دستورات و تغییر گزینه Confidence Level در پنجره SPSS، طول فاصله اطمینان تغییر خواهد کرد. در این حالت طول فاصله اطمینان برابر با 4682 دلار است. مشخص است که با کاهش سطح اطمینان، دقت برآورد فاصله‌ای بیشتر شده زیرا طول بازه کاهش یافته است.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آزمون آماری و پی مقدار (p-value)
• مجموعه آموزش‌های نرم‌افزار آماری SPSS
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• فاصله اطمینان (Confidence Interval) — به زبان ساده
• آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات

^^