زیر مجموعه چیست و علامت زیر مجموعه چیست؟ – با مثال
اگر تمام اعضای مجموعهای مانند A در مجموعهای بزرگتر یا مساوی آن به نام B وجود داشته باشند، میگوییم مجموعه A زیرمجموعهای از مجموعه B است. در مطالب پیشین مجله فرادرس با مجموعه و تعاریف مربوط به آن آشنا شدیم. در این آموزش بررسی میکنیم که زیر مجموعه چیست و مثالهایی از آن را مرور خواهیم کرد. ابتدا در قالب چند مثال عددی خواهیم دید که مجموعه چیست و چه ویژگیهایی دارد، سپس به بیان تعریف ریاضی مجموعه خواهیم پرداخت و مثالهای بیشتری را بررسی میکنیم.
- تعریف زیرمجموعه را خواهید شناخت.
- یاد میگیرید زیرمجموعه سره یا محض چه معنایی دارد.
- با تعداد زیرمجموعههای یک مجموعه آشنا خواهید شد.
- میآموزید مجموعه توانی چیست.
- با بررسی چند مثال متوجه میشوید مفهوم زیرمجموعه چیست.
- یاد میگیرید که چگونه زیرمجموعههای یک مجموعه را تشخیص دهید.
تعریف زیر مجموعه چیست؟
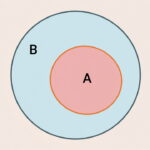
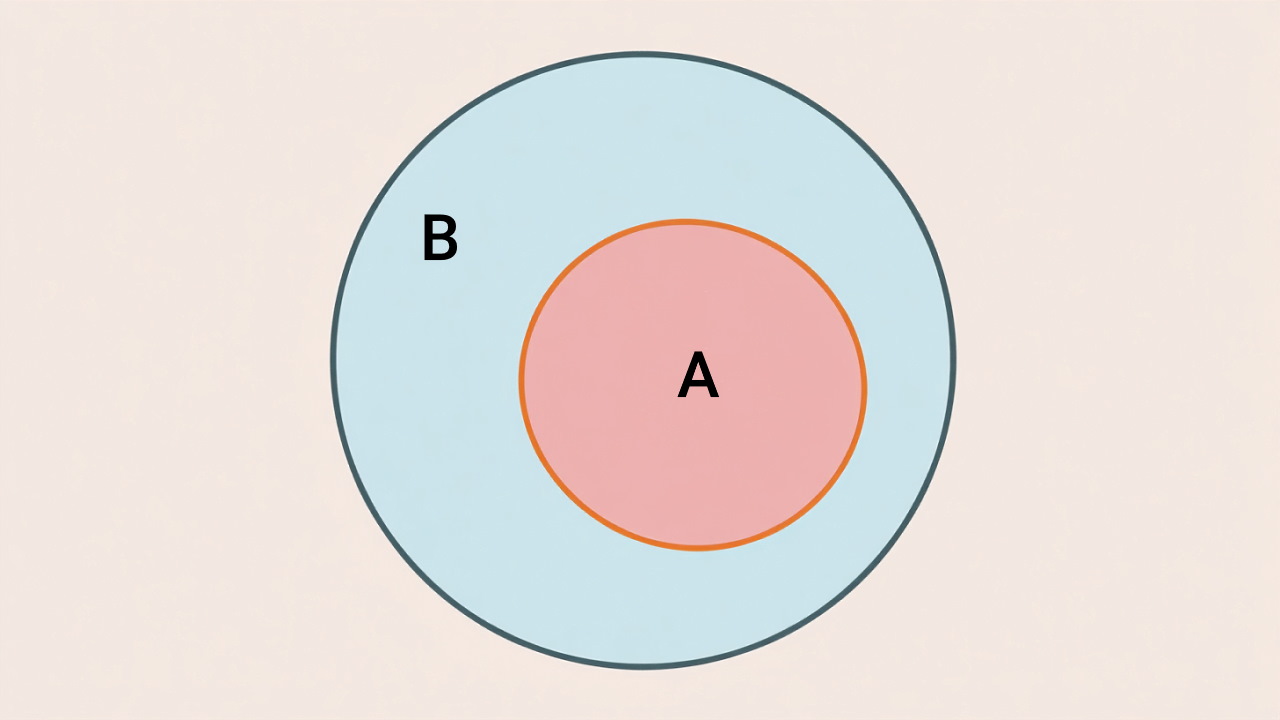
در نظریه مجموعهها مجموعه A را یک زیرمجموعه از مجموعه B مینامیم، اگر هر عضو از A در B وجود داشته باشد. زیرمجموعه را با نماد نشان میدهیم. پس اگر A زیرمجموعه B باشد یا ، تمام اعضای A در B پیدا میشوند.
جدول زیر معنای نمادهای زیر مجموعه در درس ریاضی را نشان میدهد:
| نماد | مفهوم |
| یک زیرمجموعه از ... است. | |
| زیرمجموعه ... نیست. |
در ادامه چند مثال از زیرمجموعه را بیان میکنیم تا بهتر متوجه شوید زیر مجموعه چیست و چه ویژگیهایی دارد.
چند مثال از زیر مجموعه
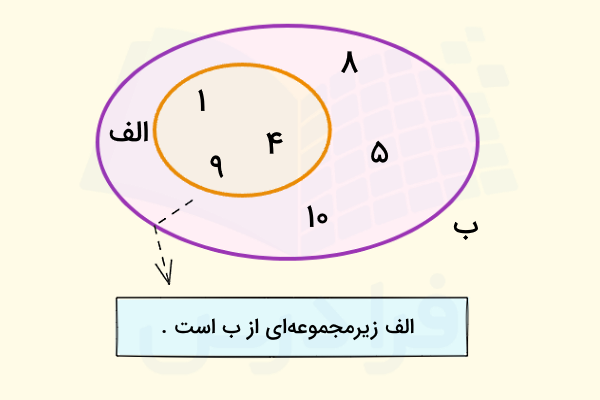
فرض کنید مجموعههای {4 ,2 ,1} = A و {5 ,4 ,3 ,2 ,1} = B داده شدهاند. مجموعه A را زیر مجموعه B میگوییم، زیرا هریک از اعضای A در B نیز هستند. این گفته را با علامت ریاضی زیر نشان میدهیم و میگوییم A زیر مجموعه B است:
در آموزش «نمودار ون — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)» با نمودار ون آشنا شدیم. اگر بخواهیم مفهوم زیر مجموعه را برای این مثال با نمودار ون نشان دهیم، شکل زیر را خواهیم داشت:
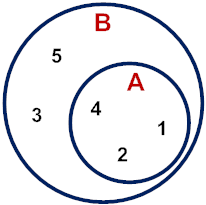
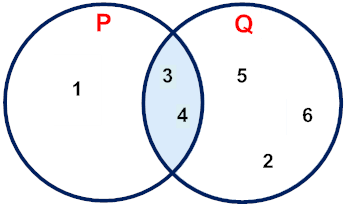
بنابراین، اگر از ما بپرسند، رابطه دو مجموعه A و B این مثال چیست، میگوییم A زیر مجموعه B است. اکنون دو مجموعه {4 ,3 ,1} = P و {6 ,5 ,4 ,3 ,2} = Q را در نظر بگیرید. میخواهیم ببینیم رابطه این دو مجموعه چگونه است. مجموعه P زیر مجموعه Q نیست، زیرا هر عضو از P در Q نیست. برای مثال، ۱ در P هست و در Q نیست (). گزاره «P زیر مجموعه Q نیست» را به شکل ریاضی زیر مینویسیم:
نمودار ون این دو مجموعه به صورت زیر است:
یک مثال دیگر را بررسی میکنیم. دو مجموعه {5 ,4 ,3 ,2 ,1} = A و {4 ,5 ,2 ,1 ,3} = B داده شدهاند و میخواهیم ببینیم رابطه بین این دو مجموعه چیست. این دو مجموعه را میتوان به صورت نمودار ون شکل زیر نشان داد:
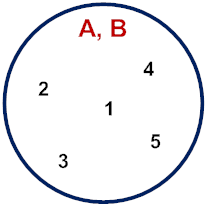
همانطور که میدانیم، ترتیب اعضا در مجموعهها مهم نیست. با نگاهی به دو مجموعه، میبینیم که هریک از اعضای A در B و هریک از اعضای B در A است. یعنی، داریم:
و
همانطور که مشاهده میکنیم، دو مجموعه برابر هستند:
زیر مجموعه سره (محض) چیست؟
تا اینجا یاد گرفتیم زیر مجموعه چیست. زیرمجموعههای به غیر از خود مجموعه را «زیرمجموعه سره» (Proper Subset) مینامند. با این تعریف، مجموعه {۲ ,۱} یک زیر مجموعه سره از مجموعه {۳ ,۲ ,۱} است، زیرا عضو ۳ در مجموعه نخست وجود ندارد. بنابراین، اگر A ⊆ B و A≠B، آنگاه A را یک زیر مجموعه سره از B مینامیم.
نکته ۱: مجموعه تهی (Ø) زیر مجموعه سره هر مجموعهای جز خودش است. بنابراین، برای هر مجموعه A، میتوان اینگونه نوشت:
A ⊇ { } یا Ø ⊆ A
نکته ۲: برای هر دو مجموعه A و B، اگر داشته باشیم: و ، آنگاه .
تعداد زیر مجموعههای یک مجموعه
میخواهیم همه زیرمجموعههای مجموعه {۳ ,۲ ,۱} = C را بنویسیم. این زیرمجموعهها در زیر آورده شدهاند:
- {۱} = D
- {۲} = E
- {۳} = F
- {۱،۲} = G
- {۱،۳} = M
- {۲،۳} = N
- {۱،۲،۳} = P
شاید تعجب کرده باشید که چرا مجموعه تهی را به عنوان یک زیرمجموعه از C فهرست کردهایم. هیچ عضوی در مجموعه تهی وجود ندارد، بنابراین هیچ در مجموعه تهی نمیتواند وجود داشته باشد که در مجموعه کامل موجود نباشد. بنابراین مجموعه تهی زیرمجموعهای از هر مجموعه است. ممکن است از خود بپرسید: آیا یک مجموعه زیرمجموعهای از خودش است؟ پاسخ مثبت است: هر مجموعهای شامل خودش به عنوان یک زیرمجموعه است. این گزاره را به صورت ریاضی زیر نشان میدهیم:
زیرمجموعهای که کوچکتر از خود مجموعه باشد، زیر مجموعه سره است. بنابراین مجموعه {۲ ,۱} زیر مجموعه سرهای از مجموعه {۱،۲،۳} است، زیرا عضو ۳در مجموعه نخست وجود ندارد. در این مثال، مشاهده میکنیم که G زیرمجموعه سرهای از C است، در واقع، هر زیرمجموعهای که در بالا فهرست شده است، زیر مجموعه سرهای از C است، به جز P. دلیل این امر آن است که است که P و C مجموعههای برابر هستند (P = C).
نکته: گاهی برخی ریاضیدانان از نماد برای نشان دادن یک زیرمجموعه و نماد برای نشان دادن زیر مجموعه سره استفاده میکنند. در کتابهای درسی از نماد استفاده شده است و ما نیز تنها به آن میپردازیم.
اگر تعداد اعضای یک مجموعه را داشته باشیم، تعداد زیرمجموعههای آن برابر خواهد بود با:
دو به توان تعداد اعضای مجموعه = تعداد زیر مجموعه ها
تعداد زیرمجموعههای سره نیز بهصورت زیر خواهد بود:
۱ - دو به توان تعداد اعضای مجموعه = تعداد زیر مجموعه های سره
بنابراین، تعداد زیرمجموعههای یک مجموعه با n = ۲ عضو، برابر خواهد بود با:
۴ = ۲2 = ۲n = تعداد زیرمجموعهها
و، تعداد زیرمجموعههای سره یک مجموعه با n = ۲ عضو، برابر خواهد بود با:
۳ = ۱ - ۲۲ =۱ - ۲n = تعداد زیرمجموعههای سره
تفاوت عضو و زیر مجموعه چیست؟
به هریک از این «چیزها»ی متمایز و منحصر به فرد مجموعه، «عضو» (Element) یا عنصر مجموعه میگوییم. اگر بخواهیم نشان دهیم که عضوی متعلق به یک مجموعه است، از نماد ∋ استفاده میکنیم. در طرف مقابل، برای آنکه نشان دهیم چیزی عضو مجموعه نیست، نماد را به کار میبریم. اما زیر مجموعه، مجموعهای است که همه اعضای آن در مجموعه مورد بحث وجود دارند. بنابراین، باید دقت کنید که زیر مجموعه خود یک مجموعه است.
مجموعه توانی چیست؟
مجموعه توانی مجموعه A که آن را با P(A) نشان میدهند، مجموعه همه زیرمجموعههای A است. مثلاً اگر مجموعه را داشته باشیم، آنگاه مجموعه توانی A بهصورت زیر خواهد بود:
حل مثال از زیر مجموعه
در این بخش، چند مثال از زیرمجموعه را بررسی میکنیم.
مثال ۱
زیرمجموعههای مجموعه {x, y, z} = R را بنویسید.
پاسخ
این زیرمجموعهها عبارتند از:
- {x} = D
- {y} = E
- {z} = F
- {x, y} = G
- H = {x, z}
- J = {y, z}
- K = {x, y, z}
- Ø
همانطور که میبینیم، این مجموعه ۸ زیرمجموعه دارد.
مثال ۲
همه زیرمجموعههای C = {۱, ۲, ۳, ۴} را بنویسید.
| زیرمجموعههای مجموعه C | |
| M = {۲, ۴} | D = {۱} |
| N = {۳, ۴} | E = {۲} |
| O = {۱, ۲, ۳} | F = {۳} |
| P = {۱, ۲, ۴} | G = {۴} |
| Q = {۱, ۳,۴} | H = {۱, ۲} |
| R = {۲, ۳, ۴} | J = {۱, ۳} |
| S = {۱, ۲,۳, ۴} | K = {۱, ۴} |
| Ø | L = {۲, ۳} |
همانطور که مشاهده میکنید، این مجموعه ۱۶ زیرمجموعه دارد. همانطور که دیدیم، مجموعه R دارای ۳ عضو و ۸ زیر مجموعه است. مجموعه C نیز ۴ عضو و ۱۶ زیر مجموعه دارد. برای یافتن تعداد زیرمجموعههای یک مجموعه با n عضو، کافی است ۲ را به توان n برسانید. یعنی اگر تعداد اعضای مجموعه A برابر با n باشد، آنگاه تعداد زیرمجموعههای A برابر با ۲n است.
مثال ۳
درستی و نادرستی روابط زیر را مشخص کنید.
الف) {۲, ۳} ⊇ {}
ب) {۲, ۳} ∋ {}
ج) {{}, ۲, ۳} ∋ {}
د) {۵, ۶, ۷, ۸} ⊇ {۵, ۶, ۷}
هـ) {۵, ۶, ۷, ۸} ⊇ {۵, ۶, ۷, ۸}
پاسخ
- پاسخ الف: درست
- پاسخ ب: نادرست
- پاسخ ج: درست
- پاسخ د: درست
- پاسخ هـ : درست
معرفی فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی
یکی از آموزشهای ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانشآموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثالهای حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و... پرداخته شده است. کار با دادههای آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش دادهها ارائه شده است.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزشهایی که برای آشنایی بیشتر با مباحث پایه ریاضی میتوانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعهها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شدهاند. موضوعات درس دوم، چندجملهایها و اتحاد و تجزیه است. در درس سوم، نامساویها، نامعادلات، طول پارهخط، ضریب زاویه و معادله خط مورد بحث قرار گرفتهاند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شدهاند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شدهاند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفتهاند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
جمعبندی
آنچه را که در این مطلب گفتیم، میتوان در موارد زیر خلاصه کرد:
- A زیرمجموعهای از B است، اگر هر عضو A در B باشد. این گزاره با نشان داده میشود.
- برای هر دو مجموعه، اگر و ، آنگاه است.
- مجموعه تهی مجموعهای است که یک زیرمجموعه همه مجموعههاست.
- هر مجموعهای زیرمجموعه خودش است. این گزاره با نشان داده میشود.
- زیرمجموعههای سره: اگر و ، آنگاه را یک زیرمجموعه سره از میگوییم.
همچنین تعداد زیرمجموعههای مجموعه A با n عضو، برابر با ۲n است. همچنین تعداد زیرمجموعههای سره این مجموعه ۱ - ۲n است.
آزمون زیرمجموعه
۱. در نظریه مجموعهها، تعریف زیرمجموعه چیست و با کدام نماد نشان داده میشود؟
زیرمجموعه حالتی است که هر عضو مجموعه B در A باشد و با نماد نشان داده میشود.
اگر همه اعضای یک مجموعه A در مجموعه B باشند، A زیرمجموعه B است و این رابطه با نماد نوشته میشود.
اگر فقط یک عضو مشترک میان دو مجموعه باشد، به آنها زیرمجموعه میگویند و نماد آن است.
یک مجموعه B همیشه زیرمجموعه هر مجموعه دیگر است و با نماد نمایش داده میشود.
در نظریه مجموعهها وقتی هر عضو مجموعه A در مجموعه B باشد، مجموعه A زیرمجموعه B خوانده میشود و این رابطه را با نماد نمایش میدهند. عبارت یا «عضویت»، برای نشان دادن عضو بودن به کار میروند و نه زیرمجموعه.
۲. برای تمایز بین عضو بودن یک شیء و زیرمجموعه بودن یک مجموعه، کدام گزینه درباره کاربرد نمادگذاری صحیح است؟
اگر x عضو A باشد از نماد x ∈ A استفاده میشود اما اگر B زیرمجموعه A باشد از B ⊆ A استفاده میشود.
اگر x عضو A باشد از x ⊆ A و اگر B زیرمجموعه A باشد از B ∈ A استفاده میشود.
هر دو حالت عضو بودن و زیرمجموعه بودن را فقط با نماد ∈ نمایش میدهیم.
عضو بودن و زیرمجموعه بودن هر دو با ⊆ مشخص میشوند.
برای نشان دادن اینکه یک شیء عضو یک مجموعه است باید از نماد استفاده کرد مانند عبارت «x ∈ A»، اما زمانی که بخواهیم زیرمجموعه بودن یک مجموعه را نسبت به مجموعه دیگر نشان دهیم از نماد مانند «B ⊆ A» بهره میگیریم.
۳. اگر برای دو مجموعه A و B، هر دو زیرمجموعه متقابل یکدیگر باشند، چه رابطهای میان A و B برقرار است؟
هرکدام میتواند عضو دیگری باشد بدون آنکه برابر باشند.
در این حالت هیچ رابطه خاصی وجود ندارد.
یکی از مجموعهها لزوما تهی است.
این دو مجموعه حتما با هم برابر هستند.
وقتی دو مجموعه مانند A و B زیرمجموعه متقابل یکدیگر باشند، یعنی همه اعضای A در B قرار دارند و همه اعضای B هم در A. پس هیچ عضوی در یکی نیست که در دیگری نباشد، بنابراین مجموعه «این دو مجموعه حتما با هم برابر هستند» درست است. «یکی از مجموعهها لزوما تهی است» نادرست است چون اگر هر دو عضوی داشته باشند و زیرمجموعه هم باشند، باز هم برابر میشوند. عبارت «هرکدام میتواند عضو دیگری باشد بدون آنکه برابر باشند» غلط است، چون برابر نبودن، یعنی عضو متفاوت وجود دارد که شرط زیرمجموعه متقابل را نقض میکند. «در این حالت هیچ رابطه خاصی وجود ندارد» اشتباه است چون برابر بودن یک رابطه مهم در این وضعیت است.
۴. اگر مجموعه A سه عضو داشته باشد، طبق فرمول تعداد زیرمجموعهها، چند زیرمجموعه سره برای آن وجود دارد و دلیل آن چیست؟
۶ زیرمجموعه سره، زیرا هر عضو میتواند یا نباشد.
۷ زیرمجموعه سره، زیرا برابر با ۷ است.
۳ زیرمجموعه سره، چون هر عضو فقط یک زیرمجموعه میسازد.
۸ زیرمجموعه سره، زیرا میشود ۸.
بر اساس فرمول ارائه شده، اگر مجموعه سه عضوی باشد، تعداد کل زیرمجموعهها یعنی ۸ است. اگر مجموعه خودش را که زیرمجموعه غیرسره است حذف کنیم، تعداد زیرمجموعههای سره میشود ۷.
۵. آیا مجموعه تهی (Ø) در همه موارد زیرمجموعه سره یک مجموعه دیگر محسوب میشود؟
مجموعه تهی هیچوقت زیرمجموعه سره نیست، فقط زیرمجموعه کلی محسوب میشود.
بله، مجموعه تهی همواره زیرمجموعه سره هر مجموعهای غیر از خودش است.
مجموعه تهی فقط زیرمجموعه سره مجموعه خودش است.
مجموعه تهی فقط وقتی زیرمجموعه سره است که مجموعه دیگر دست کم یک عضو داشته باشد.
عبارت «مجموعه تهی فقط وقتی زیرمجموعه سره است که مجموعه دیگر دست کم یک عضو داشته باشد» درست است؛ چرا که طبق توضیح، مجموعه تهی (Ø) همیشه زیرمجموعه همه مجموعهها هست، اما زیرمجموعه سره زمانی به حساب میآید که برابر با همان مجموعه نباشد. اگر دو مجموعه برابر باشند، زیرمجموعه سره محسوب نمیشوند. پس برای هر مجموعهای با حداقل یک عضو، مجموعه تهی زیرمجموعه سره آن است. اما نسبت به خودش زیرمجموعه سره نیست، چون برابر هستند. بنابراین گزینههایی مانند «همواره زیرمجموعه سره هر مجموعهای غیر از خودش است» توضیح ناقص دارد و گزینههای «هیچوقت زیرمجموعه سره نیست» و «فقط زیرمجموعه سره خودش است» نادرست هستند.













سلام وقت بخیر
چرا برای پیدا کردن تعداد زیر مجموعه از 2به توان n استفاده میشه ؟علت استفاده عدد۲ چیه؟
هر عضو از مجموعه میتواند یا باشد یا نباشد. پس هر عضو دو حالت دارد که این دو ها ضرب در هم میشوند و می شود 2ⁿ
سلام ببین خیلی عالی بود خیلی خوب توضیح دادی دمت گرم
سلام امیر عزیز.
خوشحالیم که از این آموزش استفاده کردهاید.
سالم و سربلند باشید.
سلام وقت بخیر
ممنون بابت اشتراک متن
سوال دارم : تو قسمت مثال سوم گزینه “و ” نوشتید اشتباهه،
تو جمع بندی نوشتید هر مجموعه زیرمجموعه خودش هست و با نماد زیرمجموعه اکید نشون داده میشه. تناقض نداره این دو قسمت؟ درستش کدومه؟
سلام زهرای گرامی.
نکتهای به متن اضافه شد که ابهام این موضوع را رفع میکند.
سپاس از همراهی و بازخوردتان.