ترکیب گزاره های منطقی — به زبان ساده

در ریاضیات و منطق، «گزاره» (Proposition) دارای یک ارزش درستی است که به کمک اصول منطقی تعیین می‌شود. با ترکیب گزاره های منطقی ساده یا جمله‌های منطقی، گزاره‌های جدیدی ایجاد می‌شود که ارزش درستی آن‌ها به کمک گزاره‌های ساده‌ای که آن‌ها را تولید کرده‌اند تعیین می‌شوند. در این نوشتار از مجله فرادرس به بررسی نحوه ترکیب گزاره‌های منطقی و شیوه ارزش‌گذاری این ترکیبات می‌پردازیم. برای آنکه در مورد گزاره و جدول ارزش گزاره‌ها اطلاعات بیشتری پیدا کنید، بهتر است ابتدا مطلب گزاره و سورها --- به زبان ساده را مطالعه کرده باشید. البته از آنجایی که منطق به کار گرفته شده در این نوشتار برمبنای منطق ارسطویی است که در مبحث دیجیتال نیز به کار گرفته می‌شود، مطالعه مطلب منطق دیجیتال — از صفر تا صد از مجله فرادرس خالی از لطف نیست. در این نوشتار ابتدا انواع ترکیب‌های گزاره‌های منطقی را معرفی کرده و سپس در مورد هم‌ارزی‌ها بحث خواهیم کرد.

ترکیب گزاره‌ های منطقی

روش‌های متعددی برای ترکیب گزاره‌های ساده و ایجاد گزاره‌های مرکب وجود دارد. در اینجا به چند شیوه ترکیب و جبر گزاره‌ها به نام «ترکیب عطفی» (Logical Conjunction)، «ترکیب فصلی» (Logical Disjunction)، «ترکیب شرطی» (Logical Implication) یا (Material Conditional) و «ترکیب دو شرطی» (Bi-conditional) یا (Logical Equality) می‌پردازیم که در مبحث منطق بیشتر رواج دارند. جدول ارزش گزاره‌های جدید یکی از مواردی است که در این نوشتار حتما به آن اشاره خواهیم کرد.

فیلم آموزش ساختمان گسسته – مرور و حل تست های کنکور کارشناسی ارشد در فرادرس

کلیک کنید

ترکیب گزاره ها به صورت عطفی

فرض کنید p , q دو گزاره باشند. منظور از ترکیب عطفی p و q که به صورت $$p \wedge q$$ نشان داده می‌شود، گزاره‌ای است مرکب که زمانی دارای ارزش درست است که هر دو گزاره p و q درست باشند. ارزش درستی این گزاره طبق جدول زیر است:

برای مثال اگر گزاره p به صورت «امروز هوا ابری است» و گزاره q به صورت «باران می‌بارد» باشند، گزاره حاصل از ترکیب عطفی آن‌ها به صورت گزاره «امروز هوا ابری است و باران می‌بارد» نوشته می‌شود. کاملا واضح است که زمانی درستی این گزاره را می‌پذیریم که هر دو گزاره ساده تشکیل دهنده آن، دارای ارزش درست باشند.

اگر گزاره همیشه درست را با T و تناقض یا گزاره همیشه غلط را با F نشان دهیم مشخص است که $$p\wedge T\equiv p$$ و $$p \wedge F\equiv F$$ خواهد بود. توجه داشته باشید منظور از $$\equiv$$ هم‌ارزی دو گزاره است که به معنی یکسان بودن جدول ارزش آن‌ها تلقی می‌شود.

ترکیب گزاره ها با شکل فصلی

با توجه به دو گزاره p و q، منظور از ترکیب فصلی این دو گزاره، گزاره مرکبی است که به صورت $$p\lor q$$ نوشته شده و زمانی ارزش آن درست است که حداقل یکی از گزاره‌های p یا q دارای ارزش درست باشند. جدول ارزش زیر به بررسی ترکیب فصلی پرداخته است.

نکته: همانطور که در جدول دیده می‌شود، زمانی که هر دو گزاره p و q نادرست باشند، ترکیب فصلی آن‌ها نیز نادرست است.

اگر گزاره‌های p به صورت «امروز هوا آفتابی است» و q به صورت «امروز هوا خنک است» باشند، گزاره حاصل از ترکیب فصلی آن دو به صورت گزاره «امروز هوا آفتابی است یا هوا خنک است» نوشته می‌شود. کاملا مشخص است که استنباطی که در مورد درست بودن این گزاره داریم بستگی به درستی فقط یکی از گزاره‌های تشکیل دهنده آن دارد. برای گزاره همیشه درست (T) و تناقض یا گزاره همیشه غلط (F) داریم $$p\lor T\equiv T$$ و $$p \lor F\equiv p$$ خواهد بود.

نکته: با توجه به جدول ارزش برای ترکیب فصلی و عطفی مشخص است که جابجایی گزاره‌های p یا q در نتیجه ارزش ترکیب فصلی یا عطفی تاثیری نخواهد داشت. یعنی هم‌ارزی‌ زیر را برای ترکیب عطفی داریم:

$$\large p \wedge q \equiv q \wedge p$$

و همچنین برای ترکیب فصلی نیز می‌توان هم ارزی زیر را نوشت.

$$\large p \lor q \equiv q \lor p$$

قانون دمورگان در ترکیب گزاره ها

براساس قانون دمورگان، رابطه‌ای هم‌ارزی بین نقیض یک رابطه عطفی و فصلی وجود دارد. در این حالت اگر p و q دو گزاره باشند، طبق قانون دمورگان می‌توان نوشت:

$$\large \sim (p\wedge q) \equiv \sim p \lor \sim q$$

و همچنین:

$$\large \sim (p\lor q) \equiv \sim p \wedge \sim q$$

بررسی این هم‌ارزی به راحتی به کمک جدول ارزش امکان‌پذیر است. ابتدا جدول ارزش را برای قانون اول که براساس رابطه عطفی نوشته شده، ایجاد می‌کنیم.

و همچنین برای رابطه فصلی نیز داریم:

ترکیب گزاره های شرطی

فرض کنید دو گزاره p و q به صورت شرطی با یکدیگر ترکیب شده‌اند. این ترکیب به صورت $$p\rightarrow q$$ نوشته می‌شود. در این حالت p را مقدم و q را تالی می‌گویند. معمولا برای مشخص کردن گزاره شرطی از عبارت «اگر... آنگاه...» استفاده می‌شود.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

در نتیجه $$p\rightarrow q$$ را به صورت «اگر p آنگاه q.» می‌خوانیم. جدول ارزش برای ترکیب شرطی به صورت زیر است.

همانطور که در جدول دیده می‌شود، زمانی که مقدم درست و تالی نادرست باشد، ارزش گزاره شرطی، نادرست خواهد بود و در بقیه حالات، ارزش آن درست در نظر گرفته می‌شود. توجه کنید که این ارزش ترکیب شرطی طبق اصول منطقی است و اثبات یا برهانی برای آن وجود ندارد. بلکه عقل سلیم در صحت این ارزش‌ها شک نخواهد داشت. اگر مثالی در این موارد نوشته می‌شود، فقط به منظور تایید اصل و ملموس‌تر شدن اصول منطقی است.

گزاره شرطی «اگر p آنگاه q» را گاهی با عبارت‌های «p  شرط کافی است برای q» و یا «q شرط لازم است برای p» نیز بیان می‌کنند.

نکته: قابلیت جابجایی برای گزاره‌های p یا q در ترکیب شرطی وجود ندارد. یعنی برای ترکیب شرطی دو گزاره p و q، هم‌ارزی وجود نداشته و داریم:

$$\large p\rightarrow q \not\equiv q \rightarrow p$$

برای مثال عبارت «اگر امروز ابری باشد آنگاه من لباس گرم خواهم پوشید.» یک گزاره شرطی است که ارزش آن به هر دو گزاره ساده «امروز هوا ابری است.» و «من لباس گرم خواهم پوشید.» بستگی دارد. حال به عکس گزاره شرطی توجه کنید که به صورت «اگر لباس گرم ببوشم، آنگاه هوا ابری است.» مشخص است که ارزش درستی این گزاره با گزاره قبلی کاملا متفاوت است.

با استفاده از جدول ارزش‌ها می‌توان نشان داد که هم‌ارزی زیر برای ترکیب شرطی و فصلی برقرار است:

$$\large \sim p \lor q \equiv p \rightarrow q$$

جدول ارزش برای این هم‌ارزی در زیر نمایش داده شده است.

با توجه به ارزش‌های ثبت شده در دو ستون آخر جدول بالا، هم‌ارزی مورد نظر اثبات می‌شود. همچنین اگر مقدم یک گزاره شرطی همیشه درست باشد، ارزش گزاره شرطی به تالی بستگی دارد یعنی $$T\rightarrow q\equiv q$$.

همچنین اگر مقدم یک گزاره شرطی، یک تناقض باشد، ارزش گزاره شرطی همیشه درست است و آن را به یک تاتولوژی (گزاره همیشه درست) تبدیل می‌کند، یعنی $$F\rightarrow q\equiv T$$. از طرف دیگر اگر تالی یک گزاره شرطی T باشد، ارزش گزاره شرطی همیشه درست و تبدیل به یک تاتولوژی خواهد شد، یعنی داریم: $$p \rightarrow T \equiv T$$.

برعکس اگر تالی یک گزاره شرطی، F باشد، ارزش آن به ارزش مقدم بستگی دارد، یعنی $$p \rightarrow F\equiv \sim p$$.  در تصویر زیر یک تاتولوژی دیگر نیز نشان داده شده است.

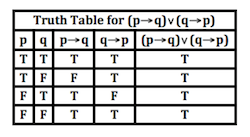
نکته: یک عبارت شرطی با عکس نقیض آن عبارت شرطی هم‌ارز است. یعنی اگر p و q دو گزاره باشند، آنگاه هم‌ارزی زیر برقرار است:

$$\large p \rightarrow q \equiv \sim q \rightarrow \sim p$$

جدول ارزش برای این هم‌ارزی نیز در ادامه دیده می‌شود:

بنابراین عبارت «اگر امروز ابری باشد آنگاه من لباس گرم خواهم پوشید.» با عبارت «اگر من لباس گرم نپوشم آنگاه هوا ابری نخواهد بود.» هم‌ارز است.

نقیض یک گزاره شرطی نیز به صورت $$\sim  (p \rightarrow q)$$ نوشته می‌شود و برای آن نیز می‌توان هم‌ارزی زیر را نوشت.

$$\large \sim (p\rightarrow q) \equiv p \wedge \sim q$$

زیرا با استفاده از هم‌ارزی‌های قبلی داریم:

$$\large \sim (p \rightarrow q) \equiv \sim (\sim p \lor q) \equiv p \wedge \sim q$$

ترکیب گزاره های به شکل دو شرطی

ترکیب عطفی دو گزاره شرطی «اگر p آنگاه q» و «اگر q آنگاه p»، ترکیب دو شرطی نامیده و به صورت «اگر و تنها اگر p آنگاه q» خوانده می‌شود. البته گزاره دو شرطی را گاهی با عبارت «p شرط لازم و کافی است برای q» یا «اگر p آنگاه q و برعکس» نیز بیان می‌کنند. نمایش ترکیب دو شرطی برای گزاره‌های p و q به صورت $$p \leftrightarrow q$$ است. جدول ارزش مربوط به ترکیب دو شرطی در زیر دیده می‌شود.

به عنوان مثال عبارت «اگر و فقط اگر 5 به ۲ بخش پذیر باشد آنگاه 5 زوج است.» یک ترکیب دو شرطی برای عبارت‌های «5 به ۲ بخش‌پذیر است.» و «5 عدد زوج است.» محسوب می‌شود. می‌توان این گزاره دو شرطی را به صورت «بخش پذیری 5 بر ۲ شرط لازم و کافی است برای زوج بودن» یا «اگر 5 به ۲ بخش‌پذیر باشد، آنگاه زوج است و برعکس» نیز بیان کرد.

همانطور که مشخص است، رابطه هم‌ارزی زیر را برای ترکیب شرطی و دو شرطی می‌توان نوشت:

$$\large p \leftrightarrow q \equiv (p \rightarrow q) \wedge (q \rightarrow p)$$

از طرف دیگر می‌توان نشان داد که عکس نقیض یک گزاره دو شرطی با گزاره دو شرطی، هم‌ارز است. به این ترتیب خواهیم داشت:

$$\large p \leftrightarrow q \equiv \sim q \leftrightarrow \sim p$$

دلیل این هم‌ارزی را به صورت زیر اثبات می‌کنیم.

$$\large \sim q \leftrightarrow \sim p \equiv (\sim q \rightarrow \sim p) \wedge (\sim p \rightarrow \sim q)$$

طبق هم‌ارزی گزاره شرطی با عکس نقیض آن می‌توان نوشت:

$$\large (p \rightarrow q) \wedge (q \rightarrow p) \equiv p \leftrightarrow  q$$

برای مثال اگر عبارت «اگر و فقط اگر 5 به ۲ بخش‌پذیر باشد، آنگاه زوج است.» را در نظر بگیرید. عکس نقیض آن به صورت «اگر و فقط اگر 5 به ۲ بخش‌پذیر نباشد، آنگاه 5 زوج نیست.» مشخص است که ارزش هر دو گزاره یکسان است.

چند هم‌ارزی مهم در ترکیب گزاره ها

در ادامه به بررسی چند هم‌ارزی می‌پردازیم که در بسیاری از رابطه‌ها و اثبات قضیه‌های ریاضی مفید باشند. در اینجا گزاره همیشه درست را با T و گزاره همیشه نادرست یا تناقض را با F نشان داده‌ایم.

هم‌ارزی راستگو یا تاتولوژی (گزاره همیشه درست)

$$\large p\lor \sim p \equiv T$$

$$\large p \lor T\equiv T$$

$$\large p \rightarrow p \equiv T$$

$$\large F \rightarrow F \equiv T$$

$$\large F \rightarrow T \equiv T$$

هم‌ارزی تناقض (گزاره همیشه نادرست)

$$\large p\wedge \sim p\equiv F$$

$$\large p \wedge F \equiv F$$

$$\large  T\rightarrow F\equiv F$$

هم‌ارزی‌های دیگر

$$\large \sim (\sim p) \equiv p$$

$$\large p \wedge (q \lor r) \equiv (p \wedge q) \lor (p \wedge r)$$

$$\large p \lor (q \wedge  r) \equiv (p \lor  q) \wedge (p \lor r)$$

$$\large p \lor (p \wedge q)\equiv p\wedge (p\lor q)\equiv p$$

$$\large p\lor (\sim p \wedge  q) \equiv p \lor q$$

$$\large p\wedge  (\sim p \lor  q) \equiv p \wedge q$$

$$\large p \leftrightarrow q \equiv (p \lor q ) \rightarrow (p \wedge q)$$

$$\large p\rightarrow q \rightarrow r \equiv (p\wedge q)\rightarrow r$$

معرفی فیلم آموزش ریاضی و آمار (۲) - پایه یازدهم علوم انسانی

 درس ریاضی یکی از دروس مطرح در دبیرستان بخصوص در رشته‌های علوم انسانی است و در تعیین رتبه بهتر برای کنکور نیز به دانش آموزان بسیار موثر است. زیرا این درس در کنکور سراسری از درس‌های اصلی محسوب می‌شود. در این فیلم آموزشی، نکات کتاب درسی ریاضی و آمار (۲) برای فراگیران ارائه شده و مثال‌ها و تمرین‌های کتاب درسی به طور کامل مورد بررسی قرار می‌گیرد. معرفی و نمایش کاربرد نکات ویژه درس نیز در قالب آزمون پایانی، از نقاط قوت این آموزش محسوب می‌شود. آموزش ریاضی و آمار (۲) - پایه یازدهم علوم انسانی، شامل سه درس است که دو درس آن به ریاضی و یک درس نیز به آمار اختصاص دارد.

درس یکم این آموزش با عنوان آشنایی با منطق و استدلال ریاضی، شامل گزاره‌ها و ترکیب گزاره‌ها، ترکیب عطفی دو‌ گزاره، ترکیب فصلی دو‌ گزاره، ترکیب شرطی دو‌ گزاره و ترکیب دو‌شرطی به همراه استدلال ریاضی است. در درس دوم، موضوع تابع، توابع ثابت، چند‌ضابطه‌ای و همانی، تابع ثابت، توابع پلکانی و قدر مطلق، تابع علامت، تابع جزء صحیح و اجرای عملیات ریاضی مانند جمع و تفریق روی این گونه توابع مورد بحث و بررسی قرار می‌گیرد. درس سوم هم به مباحث آمار، شامل، شاخص‌های آماری، خط فقر، تورم، سری‌های زمانی، درون‌یابی و برون‌یابی است.

این آموزش برای دانش آموزان رشته‌های پایه یازدهم انسانی طراحی شده و به طور کامل منطبق با کتاب درسی است. زمان این فیلم آموزشی ۱۳ ساعت و ۳۷ دقیقه است.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

در صورت علاقه‌مندی به مباحث مرتبط با منطق و مبانی منطقی، آموز‌ش‌های زیر از سایت و مجله فرادرس نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• آموزش مبانی منطق و نظریه مجموعه ها
• منطق دیجیتال — از صفر تا صد
• گزاره و سورهای منطقی --- به زبان ساده

^^