انواع سیگنال — به زبان ساده

مطالعه سیگنال‌ها و سیستم‌ها به دو موضوع می‌پردازد: اطلاعات و چگونگی تأثیرگذاری آن‌ها بر پدیده‌ها. یک تعریف دقیق سیگنال، رخدادی متغیر است که اطلاعات را منتقل می‌کند، و تعریف دقیق یک سیستم، مجموعه‌ای از ماژول‌ها است که سیگنال‌ها را می‌گیرد و پاسخ‌هایی تولید می‌کند. در این آموزش با انواع سیگنال ها آشنا می‌شویم. البته اگر قصد دارید دانش خود را در رابطه با سیگنال‌ها تقویت کنید، مشاهده فیلم‌های مجموعه آموزش سیگنال ها و سیستم ها – مقدماتی تا پیشرفته در فرادرس را به شما پیشنهاد می‌کنید.

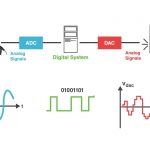
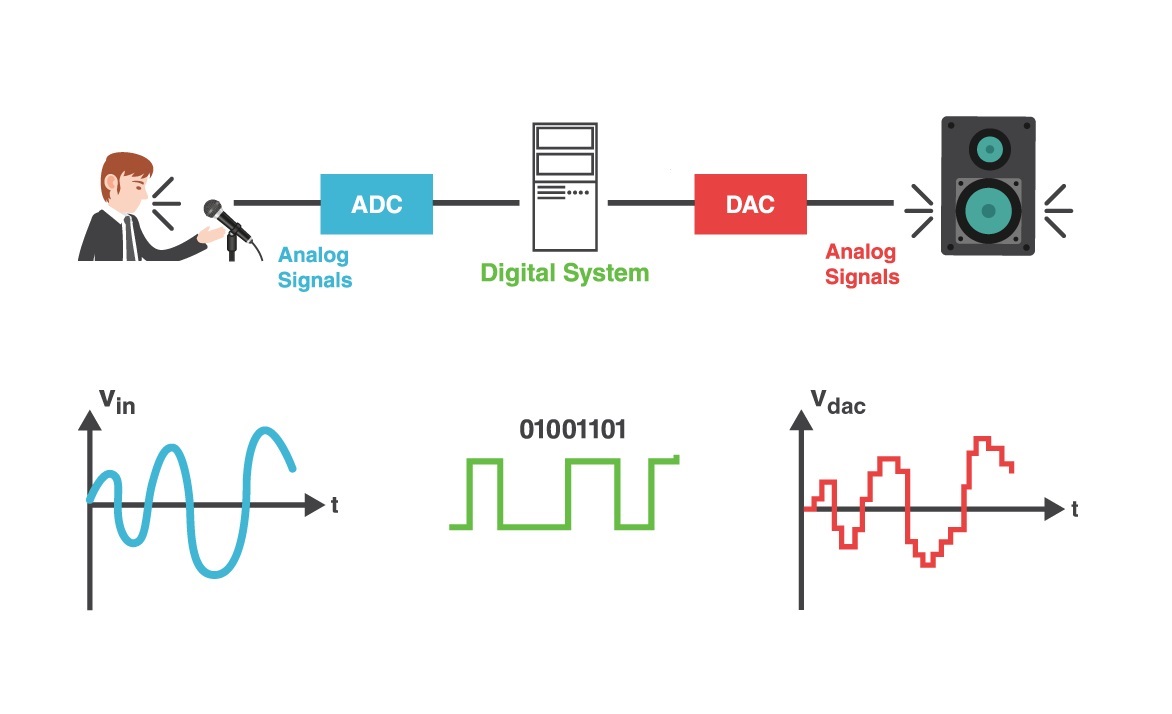
شاید فکر کردن درباره این تعاریف با بررسی یک موقعیت واقعی آسان‌تر باشد. فرض کنید می‌خواهید رباتی بسازید که روی یک خط راست حرکت کند. در اینجا، سیستم یک ربات و یک خط است. فرض کنید تجهیزی وجود دارد که به ربات این توانایی را می‌دهد تا خط راست را «حس» کند و برای این کار از یک دوربین استفاده می‌کند. در اینجا، سیگنال‌ها داده‌های بصری دوربین هستند. اما بخش سخت ماجرا اینجاست: چگونه سیگنال را بگیریم و برای آنکه بگوییم ربات در ادامه چگونه حرکت کند، از آن استفاده کنیم؟ یک حدس می‌تواند این باشد: اگر ربات در سمت راست خط باشد، آن را سمت چپ هدایت کنید و اگر سمت چپ خط باشد، آن را به سمت راست حرکت دهید. اگر هم روی خط به طور مستقیم حرکت می‌کند، حرکت خود را ادامه دهد. این نوع هدایت مناسب به نظر می‌رسد. شکل زیر نشان می‌دهد که در واقعیت چه اتفاقی رخ می‌دهد.

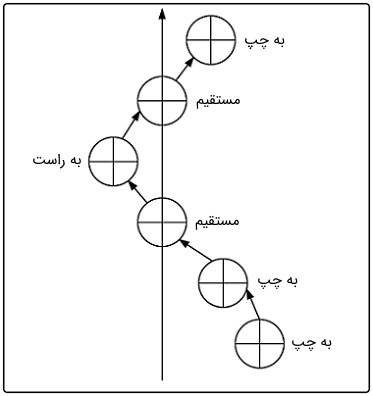
همان‌طور که می‌بینیم، در هر زمان، فراجهش خواهیم داشت. الگوریتمی که با آن بتوان این سیستم را به طور کامل مدل کرد، وجود ندارد؛ اما هدف تحقیقات در این زمینه، رسیدن به چنین الگوریتمی است. سیگنال‌ها و سیستم‌ها مفاهیمی هستند که در هر زمینه فناوری، الکترونیک و مهندسی کاربرد دارند. همان‌طور که در بالا دیدیم، کلیه قطعات سخت‌افزاری مانند ربات‌ها و رادارها که لازم است دنیای اطراف خود را حس کنند، باید بتوانند سیگنال‌ها را بشناسند و سیستم‌های خود را به طور مناسب تغییر دهند. سیگنال‌ها در سیستم‌هایی مانند رایانه نیز استفاده می‌شوند. سیگنال‌ها بین اجزای ریز در رایانه این امکان را می‌دهند تا اطلاعات و عملکرد به اشتراک گذاشته شود. این عناصر اصلی سخت‌افزار است که به عملکرد نرم‌افزار اجازه می‌دهد.

سیگنال‌

سیگنال‌ها، همان‌طور که در بالا بحث کردیم، اطلاعات را منتقل می‌کنند. البته، مفیدتر آن است که سیستم‌ها را به عنوان توابعی در نظر بگیریم که متغیر مستقل آن‌ها زمان و متغیرهای وابسته‌شان، برخی داده‌ها هستند. بنابراین، برای مثال، یک تابع سیگنال ممکن است به صورت زیر باشد:

$$\large f ( t) = 2 \times t$$

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

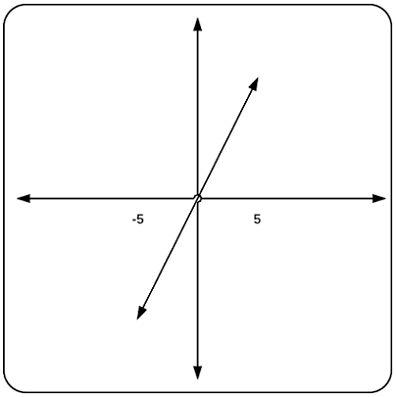
نمودار متناظر با این سیگنال به صورت زیر است.

$$f ( t) = 2 \times t$$" width="396" height="397">

یک سیستم می‌تواند تعدادی سیگنال ورودی و تعدادی سیگنال خروجی داشته باشد. مثال ربات را در نظر بگیرید. ربات می‌توانست از یک دوربین برای حس رنگ خط استفاده کند. همچنین اگر خط دارای خصوصیات فیزیکی مشخصی باشد، می‌تواند از لاستیک‌هایش برای حس جنبشی بودن خط استفاده کند. حتی اگر خط در مواد خاصی پوشانده شود، می‌تواند از حس نیروهای مغناطیسی استفاده کند. در حالی که سیگنال ورودی معمولاً توسط محیط اطراف سیستم تعریف می‌شود، سیستم کنترل بسیار بیشتری روی سیگنال خروجی دارد. سیگنال خروجی می‌تواند هر چیزی باشد که بتواند به ربات بگوید با فرمان آن چه کار کند.

به این موضوع فکر کنید که سیگنال‌های خروجی ربات چه چیز دیگری می‌تواند باشد. گفتیم که سیگنال خروجی می‌تواند هر چیزی باشد که بتواند به ربات بگوید در ادامه حرکت چه‌کار کند. برای مثال، سیگنال خروجی می‌تواند موارد زیر باشد:

• سرعت دوران چرخ‌ها
• دمای مطلوب همه چرخ‌ها
• یک بردار سه‌بعدی که موقعیت مطلوب بعدی را توصیف می‌کند.
• فاصله مطلوب از خط در گام زمانی بعدی

انواع سیگنال های دیگری نیز می‌توانیم نام ببریم، اما همه سیگنال‌ها انتخاب‌های هوشمندانه‌ای نیستند. انتخاب سیگنال خروجی برای حس کردن، به طراح سیستم بستگی دارد.

انواع سیگنال های پایه

انواع سیگنال های مختلفی وجود دارند و اغلب، سیگنال‌ها از چند سیگنال دیگر تشکیل شده‌اند. در اینجا، چند سیگنال پایه و توابع سیگنال متناظر با آن‌ها را معرفی می‌کنیم.

فیلم آموزش پردازش سیگنال دیجیتال DSP در فرادرس

کلیک کنید

تابع پله واحد

این سیگنال یک سیگنال واحد با اندازه ۱ را در زمان ۰ می‌فرستد که به مدت نامحدود ادامه دارد. اصطلاح «واحد» برای مشخص کردن این موضوع است که دامنه سیگنال برابر با ۱ است. اگر اندازه برابر با ۱ نباشد، سیگنال یک پله است. پله واحد به عنوان تابع هویساید (Heaviside Function) نیز شناخته می‌شود:

$$ \large u ( t ) = \begin {cases} 1 & \mbox {if } t \geq 0 \\\\ 0 & \mbox {if } t \lt 0 . \end {cases} $$

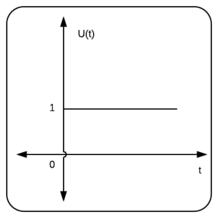
تابع پله را می‌توان مانند وصل کردن دوشاخه به پریز برق در نظر گرفت. قبل از وصل کردن دوشاخه، سیگنالی وجود ندارد. به محض اینکه دوشاخه را وصل کنیم، یک سیگنال ثابت به دستگاه متصل به دوشاخه اعمال می‌شود.

تابع ضربه واحد

این سیگنال یک تپ یا پالس واحد را در لحظه ۰ می‌فرستد. در سایر لحظات، سیگنالی وجود ندارد:

$$ \large \sigma ( t ) = \begin {cases} 1 & \mbox {if } t = 0 \\\\ 0 & \mbox {if } t \neq 0 . \end {cases} $$

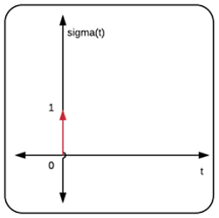
سیگنال شیب

این سیگنال رابطه خطی با زمان دارد:

$$ \large r ( t ) = \begin {cases} t & \mbox {if } t \geq 0 \\\\ 0 & \mbox {if } t \lt 0 . \end {cases} $$

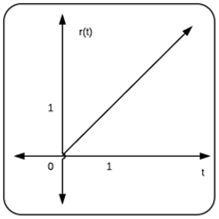
سیگنال شیب، برای مثال، سرعت سقوط جسمی از سطح شیب‌دار را توصیف می‌کند. وقتی همان جسم تحت تأثیر جاذبه سقوط کند، سرعت آن به صورت خطی افزایش می‌یابد. رابطه خطی آن، همان چیزی است که با یک سیگنال شیب توصیف شده است.

سیگنال سهمی

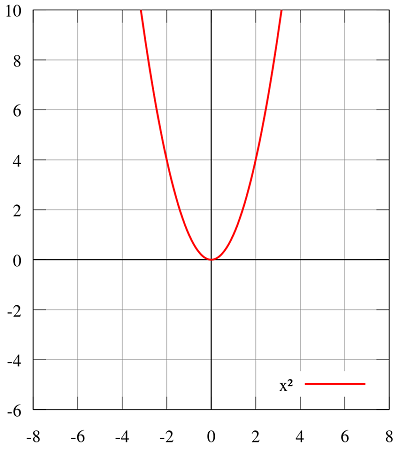
سیگنال سهمی یک رابطه مربعی با زمان دارد:

$$ \large x ( t ) = \begin {cases} \frac { t ^ { 2 } } 2 & \mbox {if } t \geq 0 \\\\ 0 & \mbox {if } t \lt 0 . \end {cases} $$

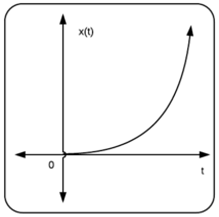
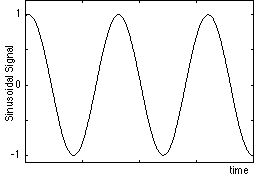
سیگنال سینوسی

این سیگنال مسیر یک سینوسی ($$\sin (x)$$ یا $$\cos (x)$$) را می‌پیماید. سیگنال‌های سنوسی بسیار مهم هستند، زیرا اساس تحلیل فوریه و سری فوریه هستند. این سیگنال‌ها اغلب در مهندسی برق مورد استفاده قرار می‌گیرند:

$$\large x ( t ) = \begin {cases} A \cdot \cos ( w _ 0 \cdot t \pm \phi ) \text { or}\\\\ A \cdot \sin ( w _ 0 \cdot t \pm \phi ) . \end {cases}$$

انواع سیگنال ها از دیدگاه ویژگی

انواع سیگنال ها را می‌توان به دسته‌های مختلفی دسته‌بندی کرد که هر یک از آن‌ها ویژگی‌های مهمی دارند. این دسته‌ها، انواع مقابل خود را نیز دارند. برای مثال، در مقابل سیگنال پیوسته، سیگنال گسسته قرار می‌گیرد. یک سیگنال را می‌توان در چند دسته تعریف کرد. در ادامه، این دسته ها را بیان می‌کنیم.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

سیگنال‌های پیوسته و گسسته

سیگنال‌های پیوسته سیگنال‌هایی هستند که در آن‌ها مقدار سیگنال در هر بازه زمانی تعریف شده است. سیگنال‌های پایه‌ای که در بالا معرفی کردیم، پیوسته هستند.

سیگنال‌های گسسته سیگنال‌هایی هستند که مقدار آن‌ها فقط در لحظات گسسته‌ای از زمان تعریف شده است؛ برای مثال، در هر یک ثانیه. نمودار یک سیگنال گسسته چیزی شبیه شکل زیر است.

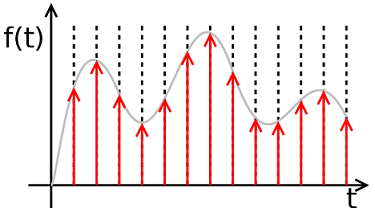
برای تفسیر و ترجمه بین سیگنال‌های پیوسته و گسسته ریاضیات مهمی وجود دارد. اغلب، در تحلیل سیگنال، از نمونه‌برداری برای تبدیل سیگنال‌های پیوسته به سیگنال‌های گسسته استفاده می‌شود. تغییر دامنه سیگنال، مانند موارد تبدیل از پیوسته به گسسته، اغلب در پردازش سیگنال مورد استفاده قرار می‌گیرد.

سیگنال‌های قطعی و غیرقطعی

سیگنال‌های قطعی سیگنال‌هایی هستند که در هر لحظه از زمان، مقدار آن‌ها نامعینی ندارد. هر سیگنالی را که بتوان با یک فرمول ریاضی، مانند تابع پله واحد، بیان کرد، قطعی است.

سیگنال‌های غیرقطعی یا تصادفی یک عنصر تصادفی در مقدار خود دارند و به همین دلیل نمی‌توان آن‌ها را به خوبی با یک فرمول ریاضیاتی تعریف کرد. این سیگنال‌ها را با استفاده از فرمول‌های آماری مدل می‌کنند.

سیگنال‌های زوج و فرد

یک سیگنال زوج است، اگر در رابطه $$f (t) = f (-t)$$ صدق کند. به عبارت دیگر، توابع زوج نسبت به محور $$y$$ متقارن هستند.

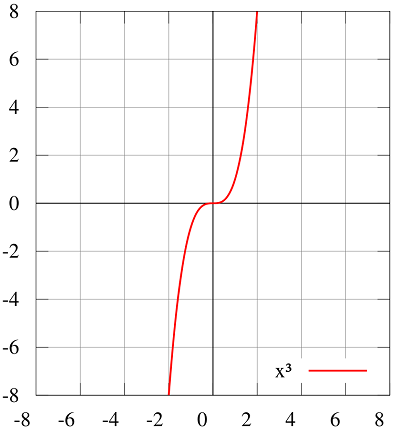
یک سیگنال فرد است، اگر در رابطه $$f (t) = - f( - t )$$ صدق کند. به عبارت دیگر، سیگنال فرد نسبت به مبداء مختصات متقارن است. برای مثال، $$\cos (t)$$ یک سیگنال زوج و $$\sin (t)$$ یک سیگنال فرد است.

یک سیگنال می‌تواند زوج یا فرد باشد یا مانند اغلب سیگنال‌ها هیچ‌کدام از این‌ها نباشد.

سیگنال‌های دوره‌ای و نادوره‌ای

یک سیگنال دوره‌ای یا متناوب است، اگر در معادله $$f (t) = f ( t + T )$$ صدق کند، که در آن، $$T$$ دوره زمانی پایه است. به بیان دیگر، اگر سیگنال $$f(t)$$ در هر $$T$$ از زمان تکرار شود، دوره‌ای است. اما یک سیگنال نادوره‌ای تکرار نمی‌شود. یک مثال از یک سیگنال دوره‌ای، هر سیگنال سینوسی، مانند $$\cos ( t)$$ و مثال از سیگنال نادوره‌ای ضربه واحد است.

سیگنال‌های حقیقی و موهومی

یک سیگنال حقیقی است، اگر مقدار هر نقطه از آن در زمان، صددرصد حقیقی و بخش موهومی آن صفر باشد. به طور مشابه، یک سیگنال موهومی است، اگر مقدار آن در هر نقطه از زمان، تنها موهومی باشد.

عملیات اساسی روی سیگنال‌ها

سیگنال‌ها را می‌توان از سیگنال‌های دیگر ساخت. در واقع، اغلب سیگنال‌ها را می‌توان به عنولن ترکیبی از سیگنال‌های کوچک‌تر و پایه‌ای‌تر تعریف کرد. عملیات اساسی روی سیگنال‌ها در دو نوع اصلی خلاصه می‌شود: آن‌هایی که به دامنه مربوط هستند و آن‌هایی که در رابطه با زمان‌اند.

عملیات روی دامنه

عملیات روی سیگنال‌ها که بر دامنه تأثیر می‌گذارند، از عملیات اساسی ریاضی، یعنی جمع و ضرب، تبعیت می‌کنند. جمع دو سیگنال موجب می‌شود دامنه آن‌ها در هر لحظه از زمان با یکدیگر جمع شود. بنابراین، جمع کردن دو سیگنال $$X_0$$ و $$X_ 1$$، سیگنال $$X_ 2$$ را نتیجه خواهد داد. این بدین معنی است که در هر زمان، اندازه سیگنال $$X_2$$ برابر با مجموع اندازه‌ سیگنال‌های $$X_0$$ و $$X _ 1$$ است.

برای مثال، اگر یک تابع پله واحد را با یک تابع شیب واحد جمع کنیم، نتیجه، سیگنالی به شکل زیر خواهد بود.

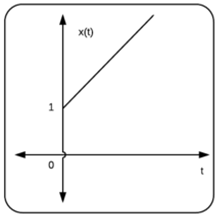
تفریق نیز فرایندی مشابه با جمع دو سیگنال دارد، با این تفاوت که در آن، اندازه سیگنال‌ها از هم کم می‌شود. ضرب و تقسیم نیز مشابه جمع و تفریق است، با این تفاوت که دامنه سیگنال‌ها در هم ضرب شده یا بر هم تقسیم می‌شود.

همین گفته‌ها برای تغییر مقیاس یک سیگنال، با ضرب یک اسکالر در آن صادق است. برای مثال، اگر یک سیگنال را در ۳ ضرب کنیم، دامنه آن در هر لحظه از زمان سه برابر می‌شود.

انجام روابط جبری بین سیگنال‌ها نیز به راحتی قابل انجام است. برای مثال:

$$\large c \cdot \big ( X _ 0 ( t ) + X _ 1 ( t ) \big ) = c X _ 0 (t ) + c X _ 1 ( t ) .$$

عملیات روی زمان

می‌توانیم زمان یک سیگنال را با جابه‌جایی، تغییر مقیاس یا معکوس کردن آن تغییر دهیم. جابه‌جایی زمانی، سیگنال $$X _ 0 ( t)$$ را می‌گیرد و آن را به اندازه $$t_ 0$$ جابه‌جا می‌کند. این جابه‌جایی می‌تواند، برای تعیین جهت جابه‌جایی، مثبت یا منفی باشد. سیگنال منتجه به صورت $$X _ 0 ( t \pm t _ 0 )$$ است.

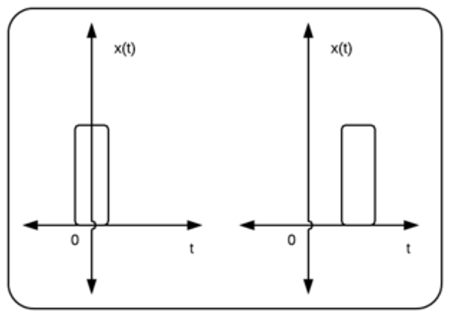
مقیاس‌بندی زمانی سیگنال را فشرده یا گسترده خواهد کرد. برای مثال، اگر یک سیگنال از $$t = -2$$ تا $$t= 2$$ تعریف شده باشد و زمان آن با ضریب ۲ مقیاس‌بندی شود، سیگنال جدید از $$-4$$ تا $$4$$ تعریف خواهد شد.

وارونگی زمانی عملیاتی است که در آن، سیگنال $$f(t)$$ به سیگنال $$f (-t)$$ تبدیل می‌شود. این سیگنال جدید، قرینه شده سیگنال ورودی نسبت به محور $$y$$ است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های پردازش تصویر و پردازش سیگنال
• آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎
• مجموعه آموزش‌های مهندسی کنترل
• آموزش پردازش سیگنال های واقعی در متلب
• تبدیل فوریه گسسته — از صفر تا صد
• تبدیل z — به زبان ساده
• سیستم LTI — از صفر تا صد

^^